双层视图筛选下多视图主动学习的高光谱图像分类

陈立伟，崔玉婕，房赫，佟志勇

1.哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001

2.黑龙江省军区, 黑龙江 哈尔滨 150001

高光谱图像分类 (hyperspectral image classification, HIC)是高光谱图像解译中的重要分支，然而高光谱图像中已标记训练样本十分稀缺，严重限制了高光谱图像分类精度的提升[1]。针对上述的小样本情景，研究学者发现主动学习可以很好地解决此问题[2]。主动学习算法的研究主要可以分为单视图主动学习(single view active learning, SVAL)和 多 视 图 主 动 学 习 (multi view active learning,MVAL)[3]。然而，单一的视图特征对图像的特征表示是有限的[4]，高光谱图像中丰富的光谱信息和空间特征信息促使多视图主动学习成为一个重要的研究方向[5]。

多视图主动学习包括2个重要的内容：多视图生成和样本选择策略[6]，其中视图的质量会直接影响样本选择策略，从而影响最终的分类结果[7]，因此，如何获得兼具差异性、互补性和多样性的视图引起学者广泛关注。Di等[8−9]提出波段的平均划分和基于相关性的光谱聚类方法；Chen等[10]提出随机划分法，利用光谱波段子集合形成多个视图。然而，这些方法仅关注到高光谱图像（hyperspectral image，HSI）的光谱特征，忽视了HSI中丰富的空间特征信息，因此得到的分类精度不高。Wang等[11]提出2D-Gabor滤波的视图生成方法；Zhou等通过三维冗余离散小波变换提取空间特征，从而产生了多个视图；Hu等[12]提出了基于3D-Gabor滤波的视图生成方法，利用不同频率和方向的3D-Gabor滤波器将原始的HSI转换为具有不同特征的空−谱特征集，再结合多视图筛选策略，选择最具充分性和多样性的视图特征形成最终视图。Xu等[13−14]通过计算视图条件互信息 (conditional mutual information, CMI)来衡量 2 个视图之间的多样性，然而条件互信息的计算量大、耗时长，对于高维的HSI数据来讲，其实现难度较大。

针对上述视图间条件互信息难以计算问题，本文提出了一种视图多样性强度值衡量方法，将经过视图充分性筛选的多视图再次进行排列组合，计算每个组合下的多样性强度值，选择多样性强度值最大的一组排列组合作为最终视图特征。传统基于条件互信息的视图多样性筛选的数值计算对象是三维HSI数据，而本文计算多样性强度值是面向HSI像元，计算视图间对应像元特征向量（即光谱曲线）的相似性，从而实现了低维中视图多样性强度值计算，有效地减少了计算量，使得本文提出的多视图主动学习在保持HSI分类精度的同时，有效地减少耗时，降低时间成本。

1 双层视图筛选策略下多视图主动学习算法框架

近年来，越来越多学者发现HSI数据包含有丰富空间信息，尽管对空间信息的提取方式各有异同，但是都认同空间信息对HSI分类的重要贡献[15−16]。其中，对高光谱图像进行3D-Gabor滤波将高光谱图像的光谱信息和空间信息相结合的方法获得广泛关注。为了使最终获取的多视图特征同时具有差异性、互补性和多样性的特点，本文引入了双层视图筛选策略对3D-Gabor滤波后产生的特征数据集进行2次筛选，通过计算多样性强度值，有效降低了视图筛选过程中的计算量。

基于双层视图筛选策略下高光谱图像多视图主动学习分类框图如图1所示，其包括3个主要部分：多视图生成、多视图筛选和候选样本筛选。首先，对原始HSI采用Z个不同频率和方向的3D-Gabor滤波器进行滤波，得到与原始高光谱图像尺寸相同、兼具空间−光谱信息的Z个数据立方体。然后，进行双层视图筛选，先利用Fisher’s (FR) 准则[12]衡量全部Z个 3D-Gabor立方体的类别可分性，再将类别可分性按大小进行排序，选择其中FR值最大的X个3D-Gabor立方体，然后从这X个立方体中选择Y个（Y≤X）个彼此最不相似的立方体，将这Y个数据立方体作为Y个多视图进行后续的多视图主动学习。最后，利用Y个视图训练Y个分类器，并分别预测全部样本的类别标签，利用分类器间预测结果的不一致性找出信息量最大的未标记样本，并交给人工专家标注，加入分类器训练集，进而使用扩充后的训练样本集继续训练Y个分类器，依次迭代，直到满足设定的最大迭代次数或最终的分类精度达到预设值。

图1 双层视图筛选策略下高光谱图像多视图主动学习框图

2 多视图生成与多视图双层筛选策略

2.1 基于 3D-Gabor滤波的视图生成方法

Gabor滤波器由于其能够从光谱和空间域提取相关信息，可获得最佳的联合时频分辨率，因此被广泛应用于特征提取。3D-Gabor滤波器的数学模型可以表示为

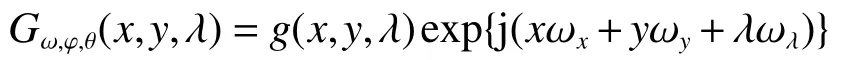
式中： ω 为波向量的中心频率，φ为向量和光谱维度的夹角，θ是样本的特征向量在地面x、y上的投影与x轴的夹角， ωx、ωy、ωλ分别为样本的特征向量在高光谱图像的横纵坐标轴x、y和光谱方向上的投影，g(x,y,λ)是在 (x,y,λ)域的三维高斯包络线，其他因子为指数谐波。

为了得到多个3D-Gabor滤波器，通过改变φ和 θ值可获得多个3D-Gabor滤波器，文中的 φ和θ分别选取 (0、π/4、π/2、3π/4)。需要特别说明的是，当 φ取值为0时，θ的值也受限于0，因此实际只有13个方向；为了获取不同尺度的纹理特征，本文还选取了5个不同的频率值 ω进行计算，分别是(1/4、1/8、1/12、1/16、1/20)。高光谱图像经过3D-Gabor滤波后，得到65个在频率和方向上不一样的高光谱图像特征立方体，这些3DGabor立方体与原始高光谱图像尺寸完全相同。

2.2 基于 FR 准则的视图充分性筛选

FR准则利用类间和类内的散度矩阵衡量每个3D-Gabor立方体的类别可分性，确保筛选后的视图具有充分性，对于视图m,m∈ (1,2,···,Z)，其FR值的计算表达式为

式中：Ds为初始已标记样本集，r为地物类别数，(µi−µj)(µi−µj)T为第i类与第j类均值类间散射矩阵 ， ( µi−x)(µi−x)T+(µj−x)(µj−x)T为 第i类与 第j类的方差类内分散矩阵。FR值越大表明对此视图的类别区分能力越强，即视图的充分性越强。因此，本文中通过计算Z个视图下的FR值，选择前X个最大的FR值对应的视图，进行下个阶段视图多样性筛选。

2.3 基于视图多样性强度值的视图多样性筛选

传统条件互信息的视图多样性筛选方法通过计算视图间条件互信息测度来选出彼此最不相似的几个数据立方体，然而条件互信息计算对象是三维HSI立方体，因此计算量大、耗时长，尤其对于高维的高光谱图像数据来讲，其实现难度较大。针对上述问题，本文计算多样性强度值是面向HSI像元，计算视图间对应像元特征向量（即光谱曲线）的相似性，从而实现了低维空间下视图多样性的衡量，有效地减少计算量。其主要流程如下：

1）首先，计算从X个视图中选取Y个视图存在k=种组合可能性，Gl（l=1,2,···,k）表示其中的第l种组合。

2）计算排列组合下的多样性强度值DI，第Gl个组合下的视图多样性强度计算公式为

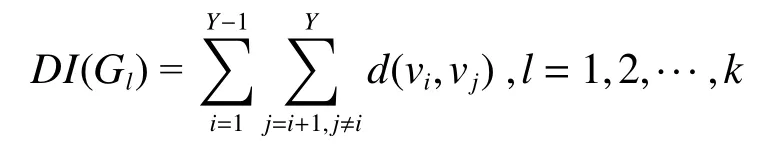
式中：d(vi,vj)表示视图vi和视图vj之间的多样性，vi和vj均为第Gl种排列组合下包含的视图。d(vi,vj)计算公式为

式中： | •|为取绝对值，A和B为视图vi和视图vj对应的二维矩阵，mn是HSI的图像大小，A和B每行代表一个像元的光谱曲线，A和B是矩阵A和B的所有元素的平均值。d(vi,vj)∈[0,1]，若d(vi,vj)=0，则说明视图vi和视图vj完全不相关，即多样性最强；若d(vi,vj)=1，则表示视图vi和视图vj完全相关，多样性最弱。

3）将k种组合下k个多视图强度值DI进行排序，选取前Y个最小的DI值所对应的视图，将其作为最终的Y个视图。

3 样本采样策略

本文采用的样本采样策略基于各个视图预测结果的不一致性。通过比较不同分类器对样本的不同预测结果的个数，衡量样本的不确定性，从候选集选出不同预测标签个数最多的样本进行查询，该方法称为自适应最大不一致策略(adaptive maximum disagreement, AMD)[8]，具体表达式为

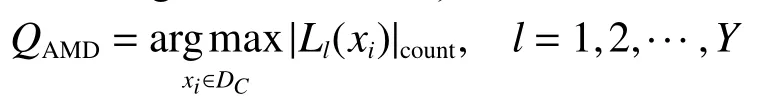
式中：Ll(xi)为第l个分类器对样本xi的分类结果，共有Y个分类器；DC为候选集； | •|count表示不同元素的个数。

通过计算候选集中所有候选样本的QAMD值，选取值最大的c个候选样本经过人工标注后加入至训练集，进行下一轮迭代。

4 实验结果与讨论

4.1 实验数据集

为了验证本文提出的双层视图筛选策略的有效性，本文选取了2幅常用的高光谱图像，分别是Indian Pines数据集和Salinas数据集。

Indian Pines数据集中包含了大量的农林场景，具有相似光谱信息的地物类别给此数据集下的分类识别带来很强的挑战性。其图像大小为145 像素×145 像素，即包含 21 025 个像元，空间分辨率可达20 m，去除噪声波段后，最终剩余200个波段用于分类识别。但是以上21 025个像元中只对10 249个像元进行了16个类别的标定。

Salinas数据集是在美国的Salinas山谷中拍摄获取的，其空间的分辨率达到了3.7 m，去除噪声和水吸收波段后，剩余204个波段用于后续分类，其图像大小为512 像素×217 像素，经过类别标注后，54 129个样本被标注为了16个类别。

4.2 实验设计

本文采用的分类精度评价指标为总体精度(overall accuracy, OA)、平均精度 (average accuracy,AA) 和 Kappa 系数。所有实验均在 Intel (R) Core(TM) i5- 10210U CPU @ 1.60 GHz 的 MATLAB R2018a 中进行。

为了验证本文基于视图多样性强度值的多视图主动学习方法的有效性，本文实验结果将分别与其他4种方法进行比较：第1种方法是光谱平均分割法[7](spectral uniform slicing, SUS)；第 2 种是3D-Gabor滤波产生多视图后随机筛选视图(3D-Gabor and random selection, 3D-Gabor-RS)， 其属于无视图筛选下的空−谱多视图主动学习算法；第3种是3D-Gabor滤波后分别学习单个视图的类别区分能力后，将类别区分能力最强的Y个视图 组 成 多 视 图[13](3D-Gabor and selection based single-view learning, 3D-Gabor-SV)，其属于一层视图筛选下的空−谱多视图主动学习算法；第4种是3D-Gabor滤波后基于多视图条件互信息筛选多 视 图[14](3D-Gabor and selection based conditional mutual information, 3D-Gabor-CMI)。

所有实验均选用相同参数的MLR分类器，样本筛选策略均使用上述的AMD采样策略，其中c值取15，即每次迭代根据采样策略从候选集选择15个未标记样本；学习迭代次数为20。涉及3D-Gabor滤波器的算法中，均采用相同参数的3D-Gabor滤波器进行视图生成，得到65个不同频率和方向的3D-Gabor立方体。为了避免实验的随机性，每组实验重复10次后计算平均值。主动学习通常是一个迭代过程，文中涉及的所有主动学习均为迭代算法，因此后续中运算时间均是指训练时间与测试时间之和，即从初始已标记样本开始第一次迭代训练至所有的训练完成，输出最终分类结果的时间总和。

4.3 实验结果

实验1比较不同算法下多视图主动学习分类效果。Indian Pines数据集和Salinas数据集下，初始训练集均随机选取每类别5个标记样本，Indian Pines数据集和 Salinas数据集中，3D-Gabor-CMI算法和本文算法中X取10，最终的视图个数均为6个，即2种算法下的Y值取6。Indian Pines数据集上，5种不同算法的分类性能可由表1对比得出，每个评价指标下的最优值已用粗体标明。

表1 Indian Pines数据集不同算法下分类结果对比

SUS算法是将原始光谱特征平均分割后产生多视图，然而光谱波段分割使每组波段的地物区分能力被削弱，此算法仅利用了光谱特征，其分类性能远低于另外4种空−谱分类算法，如与3DGabor-RS相比，OA精度要低22.23%，说明高光谱图像的空间特征对类别区分的重要性；3D-Gabor-RS算法虽然提取空间特征产生了多视图，但是由于缺少视图筛选过程，故其分类性能与另外3种算法相比分类性能差别明显，但是由于上述2种算法并未涉及视图筛选，故其运算时间小于另外3种算法；3D-Gabor-SV算法分别学习单个视图的类别区分能力，再将类别区分能力最强的几个视图组成多视图，与3D-Gabor-RS相比，OA精度提升了6.28%，该算法种虽然包含了视图筛选过程，但是视图筛选过程既要保证多样性又要保证充分性，故其分类性能与另外2种算法相比稍显逊色；3D-Gabor-CMI和本文算法分类性能差别不大，但就运算时间来看，本文算法的运算时间远小于3D-Gabor-CMI，说明本文算法在低维空间下视图多样性的衡量，在保证分类精度的同时，有效地减少了计算量。

Salinas数据集上，5种不同算法的分类性能可由表2对比得出，每个评价指标下的最优值已用粗体标明。Salinas数据集上几种对比算法的对比结果与Indian Pines数据集上类似，其中3DGabor-CMI算法和本文算法均获得明显的分类性能提升，同时本文算法所需运算时间远小于3DGabor-CMI算法，说明本文算法在减少视图筛选运算量的有效性。

表2 Salinas 数据集不同算法下分类结果对比

实验2不同初始已标记样本数量下算法稳定性。 由实验1发现，3D-Gabor-CMI算法与本文算法较另外几种算法有很大的分类性能提升，但是两者之间的运算时间有一定差距。为了进一步验证不同初始样本数量对算法稳定性的影响，分别对Indian Pines数据集和Salinas数据集上进行不同初始已标记样本数量对比，其中Indian Pines数据集的初始已标记样本数量S分别选择{5，10，15，20，25}，由于 Salinas数据集的像素规模大于Indian Pines数据集，为了更能体现差异性，Salinas数据集上的初始已标记样本数量S分别选择{5，15，25，35，45}，3D-Gabor-CMI算法和本文算法中X取10，最终的视图个数均为6个，即2种算法下的Y值取6，2种算法的分类性能和运算时间对比结果如表3和表4所示。

表3 Indian Pines数据集下不同初始样本数量时分类性能和运算时间对比

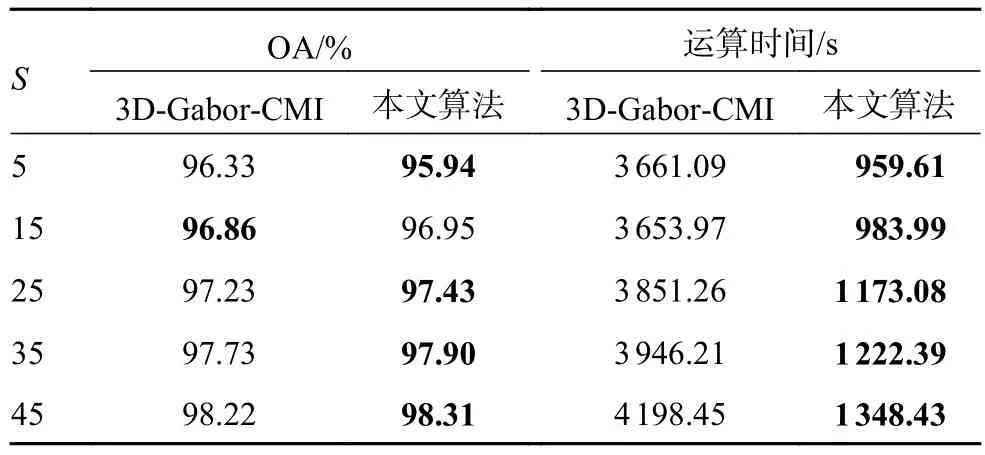
表4 Salinas数据集下不同初始样本数量时分类性能和运算时间对比

表3给出的为Indian Pines数据集下不同初始样本数量时的分类性能和运算时间对比，可以看出随着初始已标记样本数量的增加，3D-Gabor-CMI算法和本文算法的OA精度均有明显提升，且两者相差无几；就运算时间来讲，随着初始已标记样本数量的增加，本文算法的运算时间与3D-Gabor-CMI算法相比一直保持着明显优势，这也反映出了本文算法在降低视图筛选运算量方面始终保持着稳定性，进一步验证了本文算法的有效性。

表4给出的为Salinas数据集下不同初始样本数量时的分类性能和运算时间对比，其对比结果与 Indian Pines数据集下类似，3D-Gabor-CMI算法与本文算法的分类性能不相上下，但本文算法的运算时间与3D-Gabor-CMI算法相比明显降低。

为了进一步直观展示本文算法在降低运算量，减少视图筛选运算时间上的优势，在不同初始已标记样本数量下进一步取不同(X,Y)值进行实验，绘制了如图2、图3的运算时间缩减倍数曲线图，其主要展现的是本文算法与3D-Gabor-CMI算法相比运算时间减少的倍数。

图2 Indian Pines 数据集时间开销缩减倍数曲线图

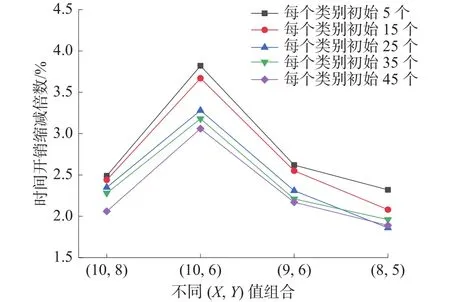
图3 Salinas数据集时间开销缩减倍数曲线图

从图2中可以看出，在Indian Pines数据集下不同初始已标记样本数量和不同(X,Y)值组合时，本文算法与3D-Gabor-CMI算法相比，时间开销的缩减倍数是不同的，进一步观察图2可以发现，无论初始已标记样本数量为多少时，在X=10、Y=6时，即(10,6)时的缩减倍数是最大的，进一步分析原因发现，在(X,Y)= (10,6)时，可以组合出210种组合，因为=210，而另外3种取值(X,Y)取值时，仅分别能组合出45种、84种和56种组合。当可以组成的组合数越多时，3DGabor-CMI算法中需要计算的视图的条件互信息次数越多，计算过程也就越繁琐，此时本文算法在低维计算视图多样性的优势越明显，因此此时的缩减倍数也就越大。在Indian Pines数据集中本文算法与3D-Gabor-CMI算法相比，时间开销缩减倍数最高可达7.42倍。从图3的Salinas数据集时间开销缩减倍数曲线图中得出与Indian Pines数据集下相似结果，即无论初始已标记样本数量为多少时，在X=10、Y=6时，即(10,6)时的缩减倍数是最大的，进一步验证了本文算法在降低视图筛选运算量的有效性和稳定性。

5 结论

针对传统多视图主动学习中视图筛选耗时大的问题，提出了基于视图多样性强度值DI的双层视图筛选策略。

1）与传统多视图主动学习算法中直接产生所需视图不同的是，本文算法首先产生远大于所需视图数量的多视图，再进行视图筛选得到需要的多视图，以此来保证视图的充分性、多样性。

2）针对传统视图多样性筛选方法计算量大、耗时长的问题，本文面向HSI像元计算2个视图像元间特征向量（即光谱曲线）的相似性，从而实现了低维空间下视图多样性的衡量，完成视图多样性筛选。

3）在 Indian Pines数据集和 Salinas数据集进行多组仿真实验对比，结果表明所提出的算法在保证与传统多视图主动学习相似的分类精度的同时，有效减少耗时，节省大量时间成本。

本文的视图生成方法依赖于不同参数的3DGabor滤波器，针对不同高光谱图像数据集，对应的合适参数无法自适应选择，未来需要在此方面深入研究；另一方面，HSI包含了丰富空间特征，如何在多视图主动学习中更好融合空-谱特征是另外一个研究重点。