汾河流域上游基流特征及其影响因素

吕向林，姬世保，仇亚琴，郝春沣，杨 月

(1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100078；2.天津科技大学滨海地下水利用与保护研究室，天津 300450)

基流是地表径流的重要组成部分，基于径流成分的传播时间，将径流划分为直接径流和基流，其中直接径流由地表产流和快速壤中流组成，基流由慢速壤中流和地下水组成[1]。由于地下水以及慢速壤中流较为稳定，变化过程较长，与直接径流相比基流对降水的响应比较缓慢。在无人类影响情况下，基流量较为稳定，是枯水期径流的主要组成部分。基流量具有保持河川径流量、维持河道内生态环境以及种群生态、通过冲沙保持河床深度等多种重要功能。流域水文循环中基流参与不饱和含水层、地下水、地表径流之间的水量交换，是水文循环的重要特征。此外，基流量也可以用来检验分布式水文模型的模拟结果是否合理。

目前基流研究主要集中在基流分割方法、基流变化特征、影响因素分析等方面，此外，生态基流最近逐渐成为研究热点。基流分割方法主要有数字滤波法、滑动最小值法、时间步长法(hydrograph separation program, HYSEP)以及水文模型法[2]。一些学者认为，滑动最小值法以径流量的下包线作为基流，将一部分洪水退水期水量算作基流量，使得基流量偏大[3]。水文模型法需要数据较多，其中物理模型的参数优化非常复杂。数字滤波法需要数据较少，易于计算机自动实现，是近年来国际上普遍应用的基流分割方法[4]。雷泳南等[5]基于数字滤波法对窟野河流域进行基流分析，发现流域基流量下降趋势极为显著，基流量变化主要驱动因素是流域内煤矿开采和地下水超采。董薇薇等[6]针对祁连山疏勒河上游流域采用数字滤波法和滑动最小值法进行基流分割，分析了基流和基流指数BFI(基流量与径流量的比值)的变化特征，并从气温和降水两方面讨论了疏勒河上游流域基流变化的主要影响因素。

1 研究区概况

汾河作为黄河的第二大支流，全长713 km，流域面积39 721 km2，流经忻州市、太原市等6市，流域面积占山西省总面积的25.5%，被誉为山西省的母亲河。近年来，人类活动影响强烈，水土流失、煤矿大规模开采、地下水超采等问题改变了汾河流域的水循环路径及水量交换过程。汾河流域基流量急剧减少，2000—2009年平均基流量仅为1956—1959年的1/8，且下游出水口多年发生断流情况，引发地面沉降、湖泊干涸、河道内生物圈崩塌、鱼类洄游受阻等一系列严重生态环境问题，严重威胁当地社会经济可持续发展。本文选取汾河上游流域(111°21′E～112°29′E，37°40′N～38°58′N)控制站兰村站数据(图1)，采用数字滤波法及HTSED对汾河流域上游地区进行基流分割，刻画基流变化特征，分析基流量变化的主要影响因素，以期为汾河流域社会经济可持续发展、生态环境建设提供依据。

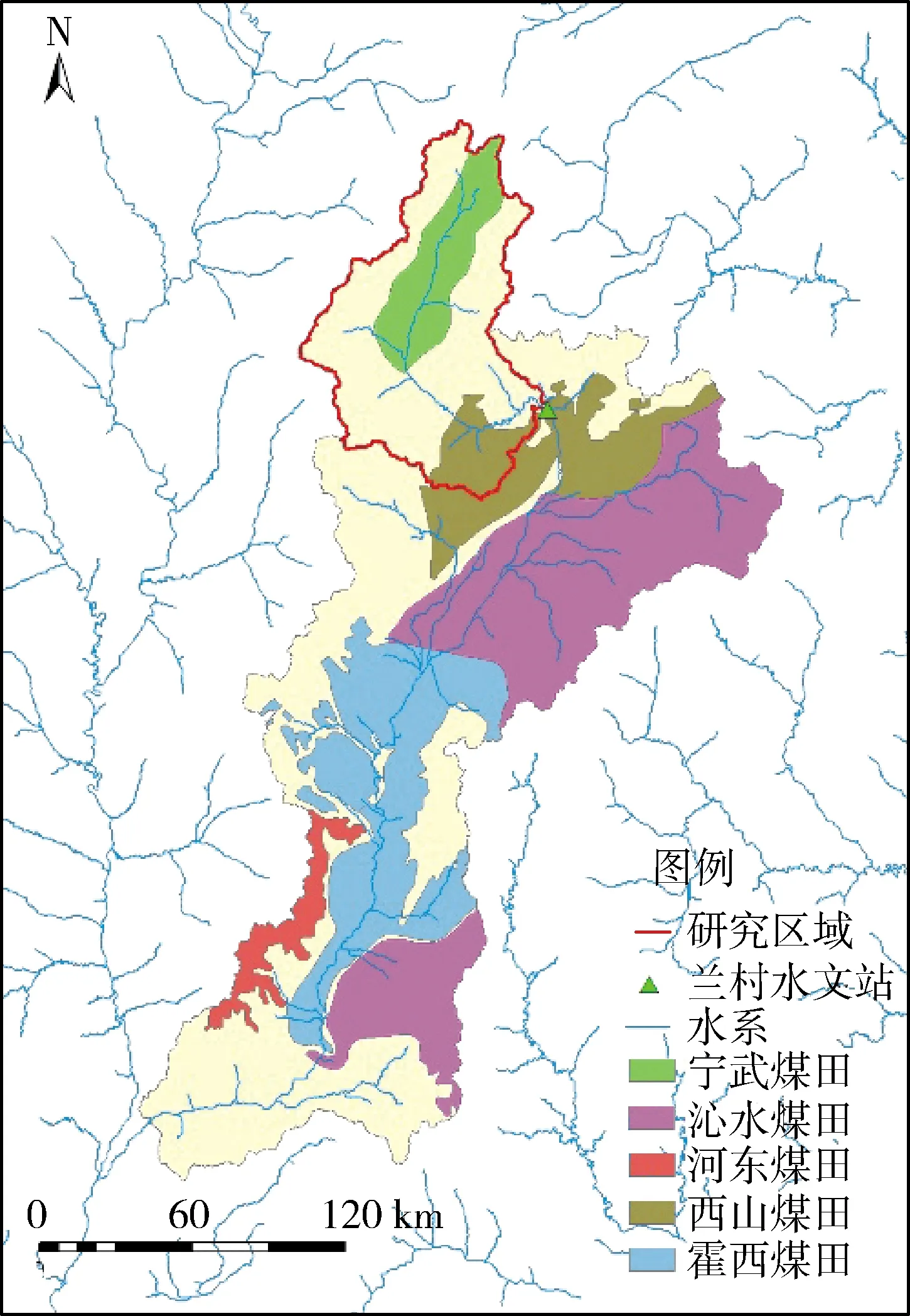
图1 汾河上游流域及煤矿分布

2 研究数据与方法

2.1 研究数据

选择汾河流域上游控制站兰村水文站1956—2016年实测日径流数据，分别采用单参数滤波法及HYSEP方法进行基流分割得到日基流量，按时间计算年、月基流量。为使单位统一，本文统一将径流量、基流量转换成径流深(mm)、基流深(mm)，即将流量与流域面积相除，反映单位面积的流量变化情况。降水数据来源于中国地面气候资料日值数据集(V3.0)，采用泰森多边形法计算并对面积进行加权平均得到平均面降雨量。1956—2008年原煤开采量数据来自《山西能源经济60年》。

2.2 研究方法

a.数字滤波法。数字滤波法是国际上普遍应用的基流分割方法，原始数据通过数字滤波器被分解为高频信号和低频信号，分别对应地表径流和基流[5,7]。本文采用Lyne于1979年首次提出，Nathan于1990年进行改进的基流分割方程：

(1)

式中：α为滤波参数；qi为i时刻的径流量，m3/s；qb，i为i时刻的基流量,m3/s；qf,i-1为i-1时刻的地表径流量，m3/s。

b.HYSEP法。HYSEP法使用3种方法划分基流：固定时间间隔法、滑动时间间隔法、局部最小值法[1,8-9]。利用经验公式计算直接径流持续时间N，时间间隔通常为介于3～11中与2N最为接近的奇数：

N=(2.95A)0.2

(2)

式中A为流域面积，km2。

c.Mann-Kendall(M-K)法。M-K法是一种非参数检验方法，被广泛应用于时间序列变化趋势特性的检验，M-K法是根据样本的秩次关系来判断其序列趋势性，受异常值影响较小也不需要样本服从特定的分布特征。通过计算Z值来定量刻画趋势变化的显著程度，常用于水文、气象等非正态数据的趋势分析。统计量Z>0表示时间序列具有上升趋势，反之则具有下降趋势。在给定显著性水平α下若|Z|≥Z1-α/2则拒绝原假设即时间具有显著的上升或下降趋势。

d.Pettitt法。Pettitt法是一种利用秩和序列检测突变的方法[10]，计算公式为

(3)

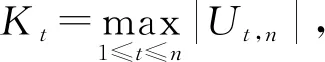
e.SCRAQ法。SCRAQ法由王随继等[11]2012年首次提出，该方法通过计算突变点前后累积降水量斜率的变化率与累积径流量斜率变化率的比值，得到降水量对径流量变化的贡献率[12]：

(4)

式中：Cp为贡献率；SPa、SPb分别为突变点后、突变点前累积降水量斜率；SRa、SRb分别为突变点后、突变点前累积径流量斜率。

3 基流变化特征

3.1 基流分割方法适宜性分析

由基流的定义可知，基流是由慢速壤中流和地下水组成，汾河流域位于半干旱半湿润地区，在枯水期基流量占径流量的大部分，二者变化趋势相差不多，而在洪水期基流较径流变化更为缓和，退水过程比径流滞后。因此，为探究两种不同基流分割方法在汾河流域的适用性及最佳参数值，选取流量过程特征明显的枯水季洪水时段进行研究。1961年9—10月洪水流量序列受人类活动影响较小且1961年为枯水年，符合研究需求。绘制数字滤波法在α分别取值0.900、0.925、0.950、0.975的情况下以及3种HYSEP法得到的基流深以及径流深曲线，如图2所示。

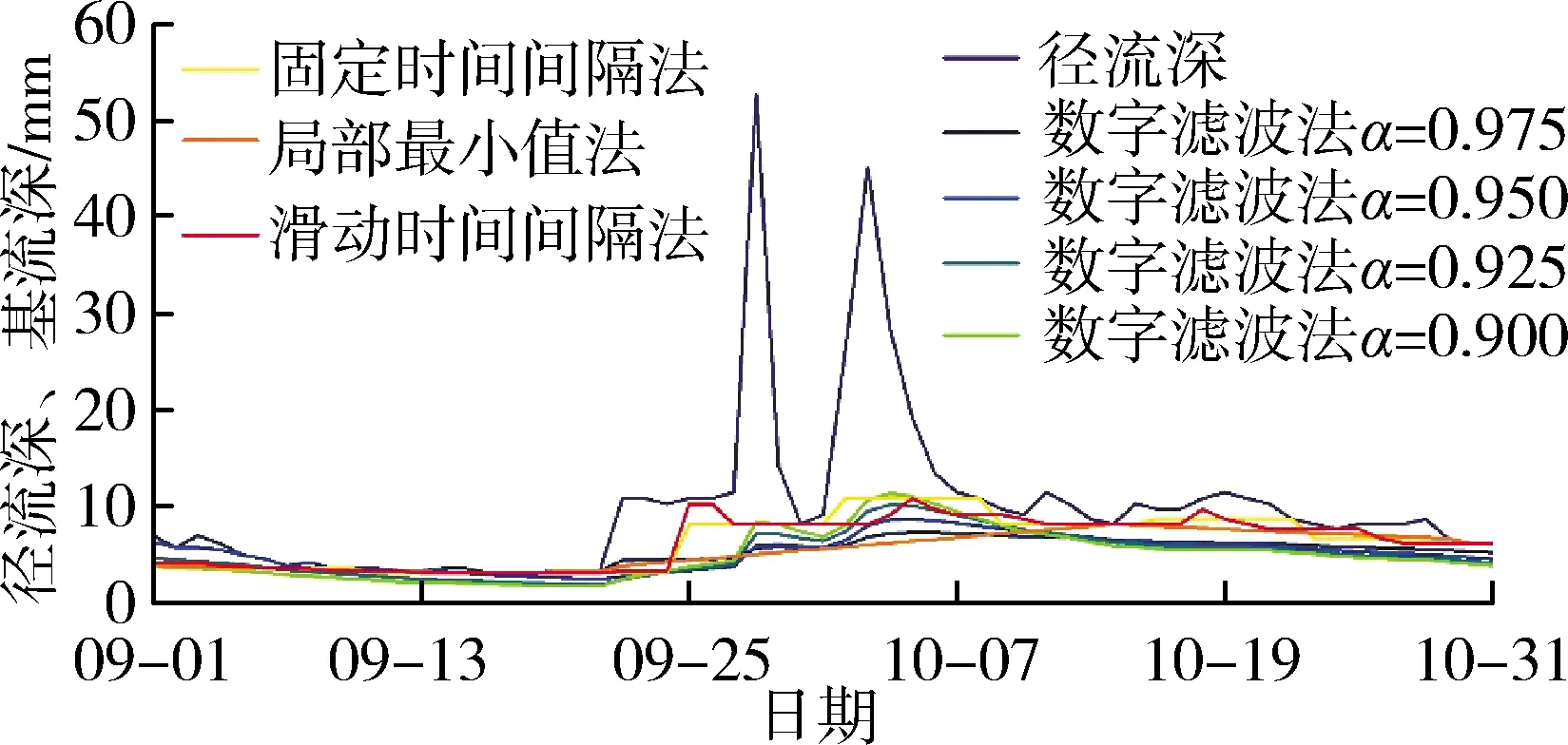
图2 1961年不同基流分割方法得到的结果

结合上文基流特征分析图2结果，可以发现固定时间间隔法、滑动时间间隔法分割的基流过程线有较多的明显拐点，出现明显的陡涨陡落现象，与实际下垫面情况不符；局部最小值法的结果虽无明显的陡涨陡落，但曲线并没有随着洪峰产生而增大；数字滤波法当α值为0.975、0.950时，在洪峰之前流量较小的时段基流深和径流深几乎相等，与基流定义相悖；α值为0.925、0.900时曲线较为平滑且趋势与径流保持一致，基本符合流域汇流规律。Arnold等[13]对美国11个流域的研究结果和Nathan等[14]对澳大利亚186个流域的研究结果证明，α取0.925时分割基流效果最好；综合参照前人成果，数字滤波法在α取0.925时可以客观地反映实际基流状况，较适宜汾河流域基流分割。

3.2 基流深年际趋势

图3(a)为1956—2016年基流深、径流深变化情况，可见二者总体均呈下降趋势，两个序列高度相关，Pearson相关系数为0.99。图3(b)为基流深的M-K检验结果，可见1956—1966年基流深无显著趋势，1967—1969年基流深呈微弱上升趋势。总体来说1956—1972年基流深保持不显著的动态变化，1973—2016年基流深总体呈下降趋势，且序列Z值为-5.88，通过置信度99%的显著性检验，下降趋势极为显著。1996年出现一次显著的波动上升，查阅资料显示1996年山西发生特大洪水，汛期降水量与往年相比增加60%，导致基流深有小幅度回升。2008—2016年基流深下降趋势减缓，有小幅增加趋势。图3(c)为BFI值变化情况，BFI值1956—2000年由0.5左右下降至0.38左右，总体上呈波动下降趋势，径流量、基流量虽然均剧烈衰减，但基流量衰减得更快，占径流量的比例减少。2000—2016年BFI值逐渐增加。

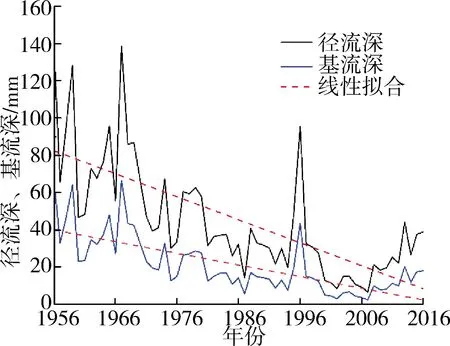
(a) 1956—2016年基流、径流趋势线

3.3 基流深突变分析

M-K法适用于单一突变点的序列计算，本研究基流深序列中存在多个突变点，采用Pettitt进行多突变点的检测，检测出第一突变点后，通过二分法把原序列分解成两个子序列分别计算突变点，重复以上步骤至序列无显著突变点存在，计算结果见表1。

Pettitt检验中，如果P≤0.01，认为检测出的突变点在统计意义上是显著的。由表1可见，1981年统计值P接近0，2008年P<0.01，则认为存在1981、2008年两个显著突变点。同时，通过M-K法计算突变时间，得到第一次突变时间为1980—1981年，两种检验方法结果一致。其他4个突变点，虽然也有突变趋势，但是并不显著。综上，1956—2016年兰村站基流量序列存在1981、2008两个显著突变点，并且根据突变点将序列分成1956—1981年、1982—2008年、2009—2016年3个时间段。

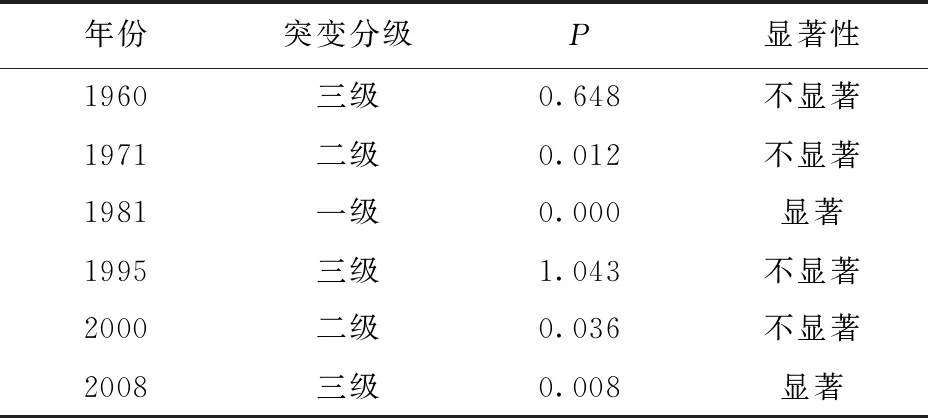
表1 基流深突变点检验

3.4 基流深年内分布变化

图4为不同年代际基流深年内分配情况。以20世纪50年代月平均基流量为基准值，计算不同年代际各月相对基准值的变化幅度，结果见表2。基流深曲线为典型“双峰型”结构，多年平均月基流深峰值大致出现在3月和8月。50年代至80年代8月平均基流深大于3月，而90年代以后3月基流深大于8月。由表2可见，年代际间基流深衰减非常剧烈，2000—2009年代年基流深仅为50年代基流深的10%，其中2000—2009年1月彻底断流，8月仅不到50年代的1%，而3月的基流深没有明显的衰减，2010年以后整体基流量有所上升，汾河流域上游从季节性河流恢复为常年河流，其中枯水期流量恢复较快，而汛期7、8、9月基流深较20世纪50年代仍有较大差距。

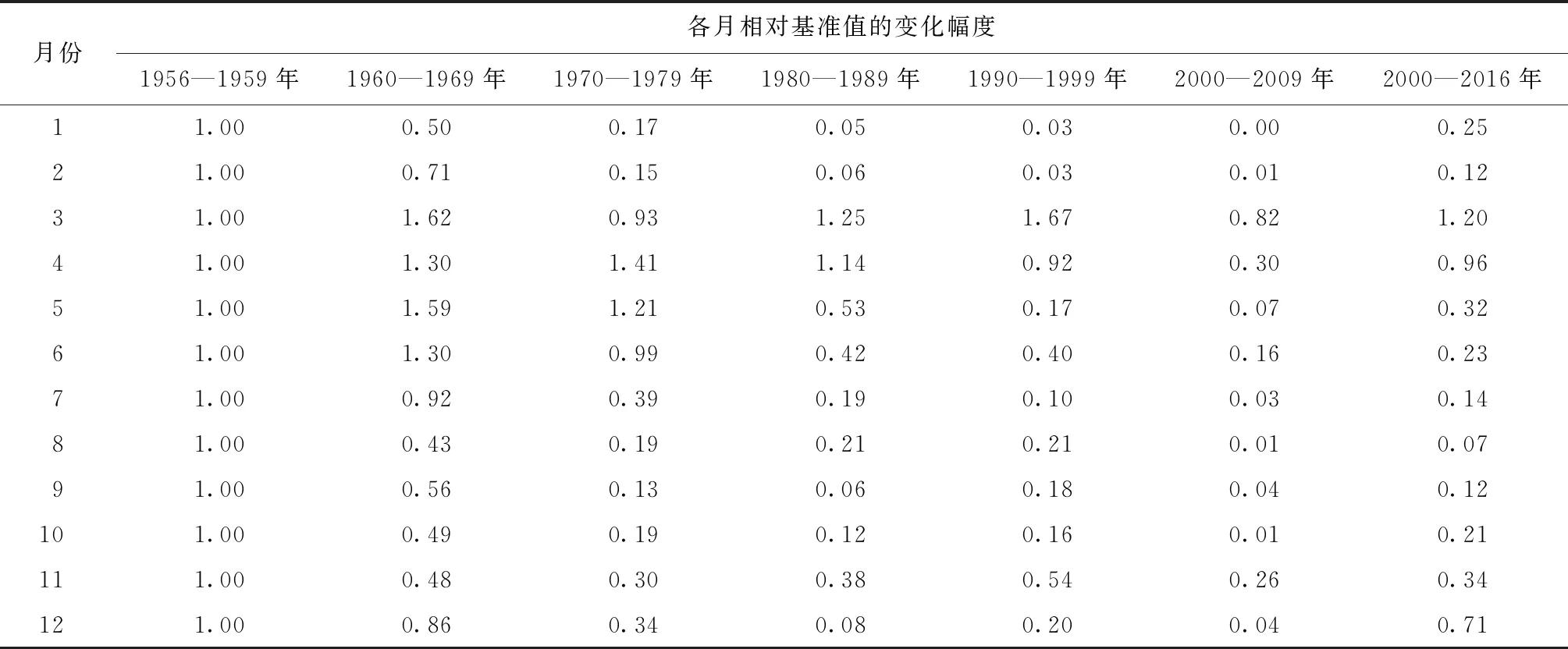
表2 基流深年代际年内衰减情况

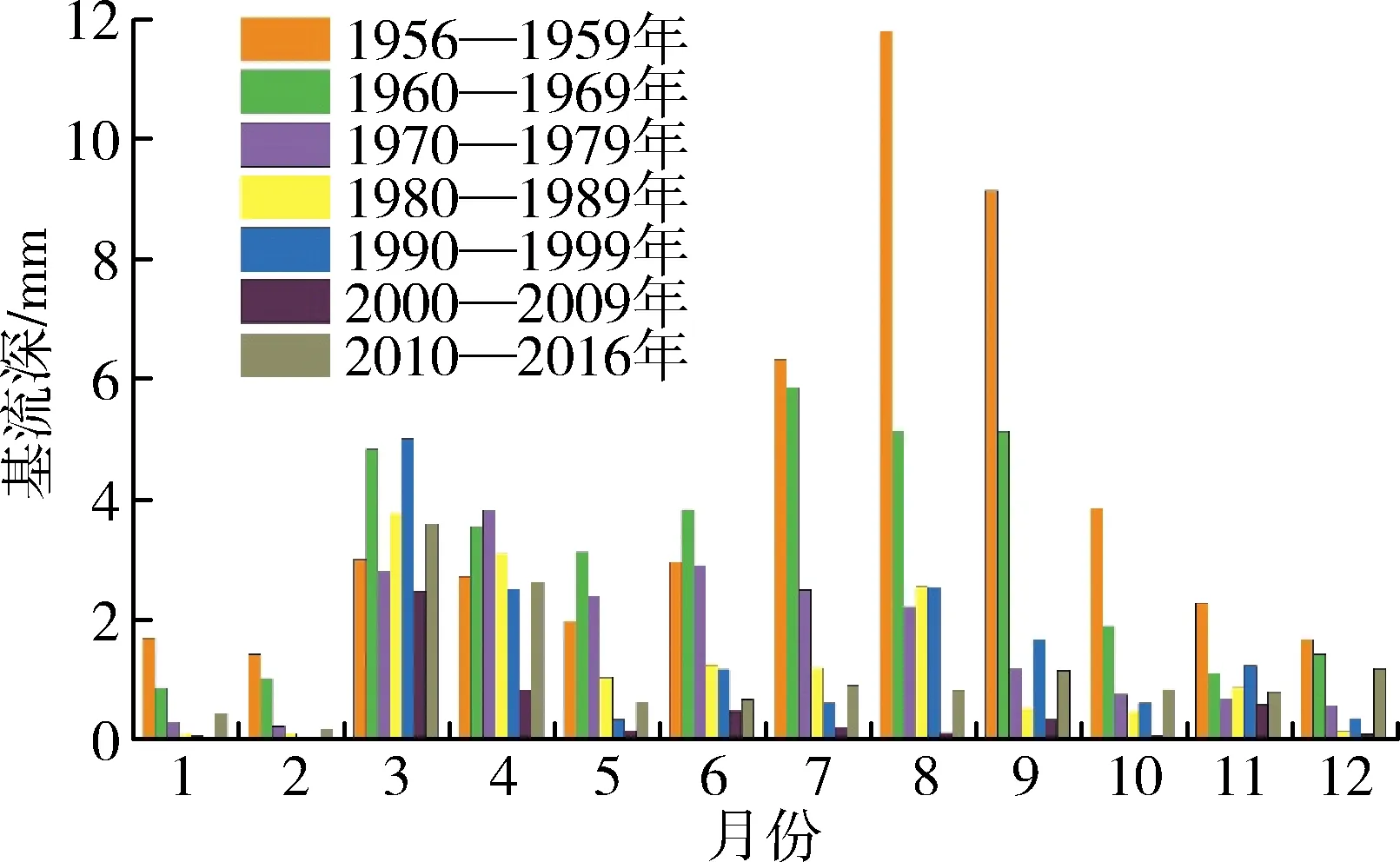
图4 不同年代际平均基流深年内分配情况

4 影响因素分析

4.1 煤矿开采

煤矿开采中会不断抽取矿涌水从而疏干浅中层地下水，地下水水位下降，形成区域性下降漏斗，导致影响半径内地下水垂向流动。煤矿开采通常距地表有一定距离，随着煤矿开采规模扩大，导致岩层移动，形成地表裂隙发育或直接造成地表塌陷，破坏浅层地下水隔水层和储水构造，使得矿区煤系地层裂隙水、上覆松散岩类孔隙水和下伏碳酸盐岩溶水相互贯通[15]，当采空区低于河底高程时，基流排向采空区而不再排向河道，随着采煤引起的裂隙加大加深，一部分地下水垂直排向采空区，使得天然基流量减少。

山西省1956—2008年煤矿产量如图5所示，煤矿产量呈指数型上升趋势，而这一阶段基流量迅速下降。用M-K法进行趋势分析，并与上文基流深趋势曲线进行Pearson相关分析，Pearson相关系数为-0.964，呈现高度负相关关系，煤矿产量的增加对基流下降产生了直接影响。《山西省煤炭开采对水资源的破坏影响及评价》表明，山西每开采1 t原煤将造成包括矿涌水在内共2.48 m3地下水损失[16]。2008年煤矿开采量为55 740万t，是1956年的35倍，是1972年的10倍。以2000—2008年年均开采量4亿t煤计算，每年山西省将损失约10亿m3地下水资源，相当于引黄入晋工程一期、二期的总引水量。

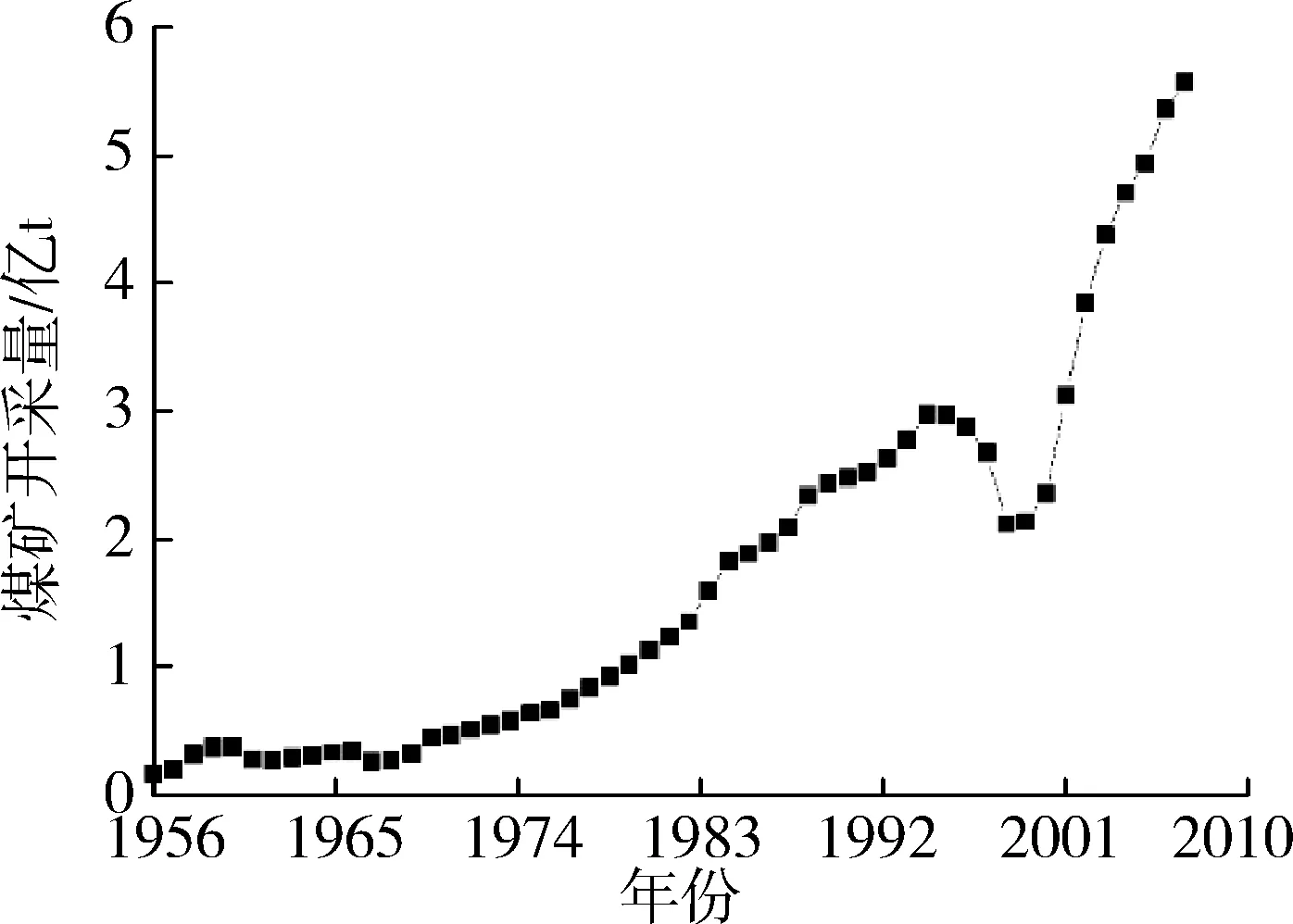
图5 1956—2008年煤矿开采量变化

4.2 地下水开采

随着社会经济飞速发展，用水需求日渐增加，地下水开采量逐年扩大[17]。20世纪80年代以前，汾河流域地下水年开采量约为4.8亿m3，1995年地下水年开采量达17亿m3，近十几年年均开采量超过30亿m3。累积超采地下水量超100亿m3。地下水严重超采导致太原盆地、临汾盆地附近深层水形成几个大范围大降深降落漏斗，至2000年，漏斗中心水位埋深46.12～129.8 m，年均下降1.2～4.6 m。2008年至今，通过汾河流域清水复流工程，引黄济晋等工程，根据2012—2014年检测数据，汾河流域地下水位年均回升0.56 m，回升速度缓慢，太原盆地、临汾盆地等漏斗区地下水位仍距地表65～85 m。地下水位相对于河道水位下降，地下水补给河道基流量减少。

4.3 降水

降水量和气温是影响径流量变化的主要气象因素，降水量改变直接导致流域产流量发生变化，而气温变化通过改变蒸发量从而影响径流量[18]。根据山西省水资源所研究成果，汾河流域上游1960—2015年蒸发无显著变化，因此本文暂不考虑气温，仅考虑降水量的变化，将非自然因素归为人类活动[19-20]。表3为突变点前后降水量与基流深变化情况，可见1982—2008年与1956—1981年相比，累计基流量斜率减少61.32%，并且累计降水量斜率下降5.95%，计算可得，降水量减少对基流量减少的贡献率仅为9.96%，而不考虑气温影响时人类活动对基流量减少的贡献率为83.19%。2009—2016年相比于1982—2008年，累计基流量斜率增加12.38%，累计降水量斜率增加10.07%，计算可得，降水量增多对基流量增多的贡献率为81.37%，而不考虑气温影响时人类活动对基流量增加的贡献率为19.63%。

表3 突变点前后降水量、基流量斜率变化

4.4 水土保持措施

水土保持能够加强水循环垂直过程并且削弱水平过程，增加降水后林地草地的拦蓄量并补给地下水，使地下水水位回升，从而实现地下水补给河道增加基流。径流、基流同时减少过程中，水土保持面积的增加使得基流衰减的比径流更加缓慢，即BFI值上升，水土保持面积与BFI关系见图6。汾河流域上游地区中,石质山区占总面积的29.4%,土石山区占29.8%,黄土丘陵沟壑区占35.5%,河谷阶地区占5.3%,沟壑密度5～8 km/km2,水土流失面积 5 317 km2,占上游地区总面积的68.8%[21]。山西省自1988年开始，持续开展三期汾河上游水土流失综合治理，水土保持面积从1988年的1 886.7 km2增加到2008年的3 175.1 km2。

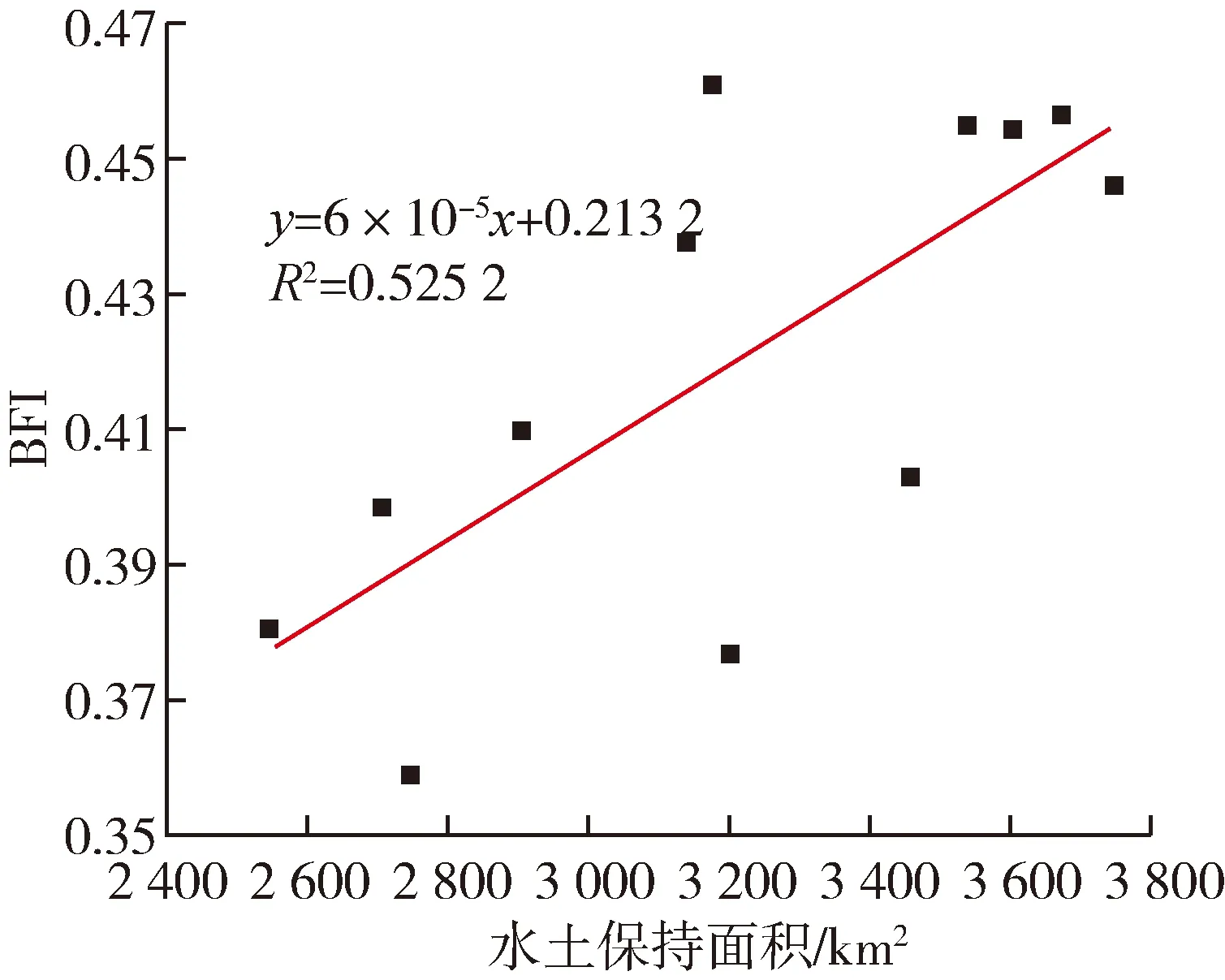
图6 水土保持面积变化

由于各影响因素数据时间跨度不同，选取1988—2008年数据，采用随机森林法对煤矿开采、降水、地下水开采、水土保持4个影响因素的重要性进行评估，将GINI指数作为评价指标，因素重要性评分用VIM表示，将计算所得各影响因素重要性评分进行归一化处理，得到煤矿开采、降水、地下水开采、水土保持VIM值分别为0.284、0.247、0.238和0.231。

综上，降水、煤矿开采、地下水开采、水土保持等均对径流和基流有造成影响[22-23]，但只有水土保持对径流起到衰减作用，而对基流起到增加作用。主要原因是地裂缝的存在，废弃开采井导致降水直接入渗地下水，深层地下水由于地下漏斗区越流补给中深层地下水[24],使得相对径流更小且更加稳定。

5 结 论

a.汾河上游流域基流在1956—2016年总体呈下降趋势，2008—2016年基流量下降趋势减缓，有小幅增加趋势。显著突变点为1981年和2008年。基流年内分布特征由20世纪60年代汛期单峰性结构转变为90年代的双峰型结构。

b.人类活动是基流变化的主要影响因素，降水的增加或减少会导致基流的增加和减少，但并不占主导地位，人类活动中煤矿开采重要性评分最高，其次是地下水开采。水土保持会导致基流小幅度增加，但重要性最低。