长江干线宜昌—浏河口段一维河网水流数学模型

李有为

(长江航道规划设计研究院，湖北 武汉 430040)

20 世纪50 年代以来，国内外相继开展了水流数值模拟的研究与应用，其中，一维水流数学模型经过数十年的研究已较为成熟，可普遍用于研究大型复杂河道长距离、长时段的水动力变化，其数值计算方法主要有特征线法、有限差分法[1]等。长江干线一维数学模型根据河道水流特点、计算精度及效率，通常以大通为界将宜昌以下河道分为宜昌—大通[2]、大通—浏河口[3]两段分别建立径流和潮流模型，而在当前新水沙条件和新型复杂江湖河网关系下，传统的两分段模型难以整体性解决长河段复杂河网的水流模拟问题，也无法实现数字航道建设要求的一体化模拟。同时，针对圣维南方程组的隐式差分格式解法中压缩存储消元法、双追赶法均存在着绝对值较小的数作除数而引起计算中断或数值不稳定的隐患，特别是在超大型河网水力计算中将显著加剧数值震荡进而降低计算精度。多年以来，人们一直在探求如何压缩系数矩阵的储存信息、用较少的单位来储存河网矩阵，用什么方法能够较快地求解超大型河网方程组并提高计算稳定性，这一直是河网水力计算中的核心问题。

为了解决上述问题，针对长江宜昌—浏河口段长达1 660 km 的超长河网，本文研发了稳定性强、精度高的基于有限体积法离散控制方程的长江航道一维河网水流数学模型。该模型采用具有TVD 特性的SLIC(slope limited centred scheme)格式计算数值通量，在处理河网交汇方面与基于三级联解算法[4]的有限差分法有所不同，其以控制体积为计算单元，实质上不需要对汊道进行额外处理，对于大型复杂河网也不用进行复杂系数矩阵的求解程序，即可以实现自动对存在支流的河段进行水力要素的计算，该模型物理过程更为清晰明了、计算更加方便快捷。

本模型可为长江航道干支联通规划、工程方案设计、维护疏浚设计、水位预测、数字航道等做技术支撑，能促进超长距离、超大范围航道综合治理工程模型试验研究，加速实现“畅通、高效、平安、绿色” 的黄金水道以及交通强国目标。

1 宜昌—浏河口段各水文站区间来流特点

长江中下游流域面积达80 万km2，覆盖区域广阔，沿线气候条件复杂多变，依靠数量有限的控制水文站难以准确计算出站与站之间的未知区间来流量，而超长一维河网模型建立的重点、难点是能否平衡同期沿线水量、率定出合理糙率等因子。因此，在建模之前需要通过主要水文站点的实测数据分析宜昌—浏河口段各水文站区间来流特点及水量平衡情况。

1.1 宜昌—大通河段

宜昌—大通河段主要支流为清江、松滋口、太平口、江汉运河、藕池口、汉江等6 条，主要入汇湖泊有洞庭湖、鄱阳湖，对应支流湖泊下游最近的水文站点分别有枝城站(清江)、沙市站(松滋口、太平口、江汉运河)、监利站(藕池口)、螺山站(洞庭湖)、汉口站(汉江)、大通站(鄱阳湖)。

从2018 年全年各主要水文站点的流量过程统计(图1)、水文站点区间流量统计(图2)来看:区间出入流对干线相邻站流量影响比较明显，对峰现时间则影响不大；在考虑主要支流湖泊出汇情况后，上下游最近水文站点的流量基本平衡，但仍然存在未经统计的次级水源出入(如毛细支流、局部降雨产汇流、人工取排水工程、蒸发下渗等)，具体而言，该部分水流占下游最近水文站流量比绝对值在10%以内的河道在全年90%以上时间的为宜昌—螺山段，螺山—汉口段、九江—大通段未知水流占比较多，特别是螺山—汉口段水流占下游最近水文站流量比绝对值均大于2%，九江—大通段水流占下游最近水文站流量比绝对值在2%以内的河道占全年时间仅25.2%，见表1。可见，螺山—汉口段、九江—大通段的区间未知水量需要重点考虑。

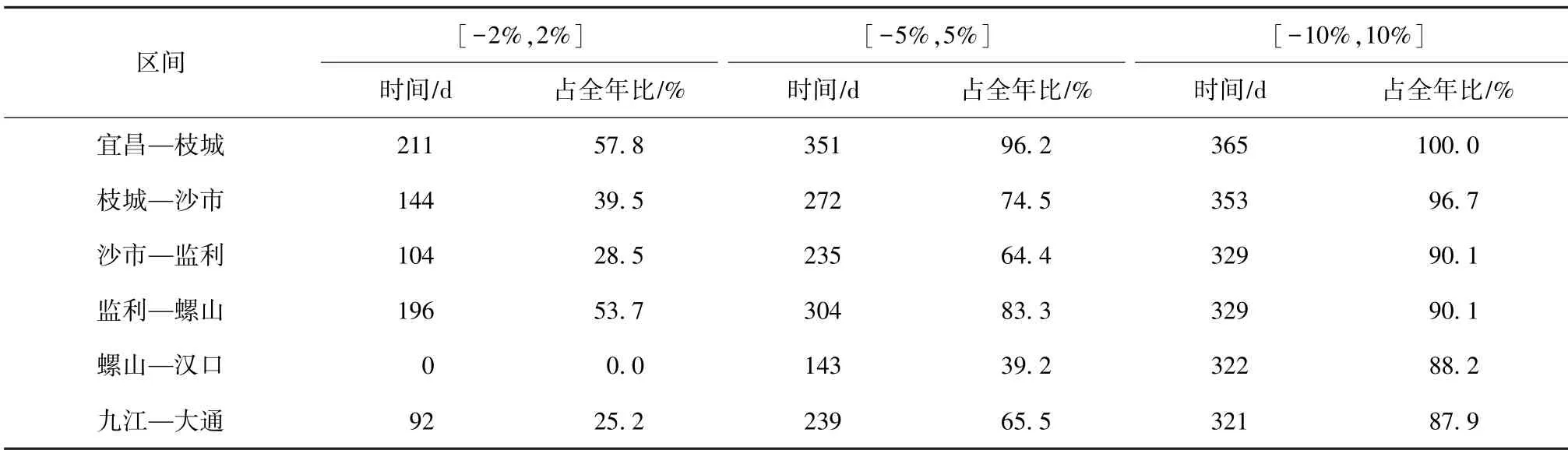
表1 日均区间流量占下游最近水文站流量比对应的时间

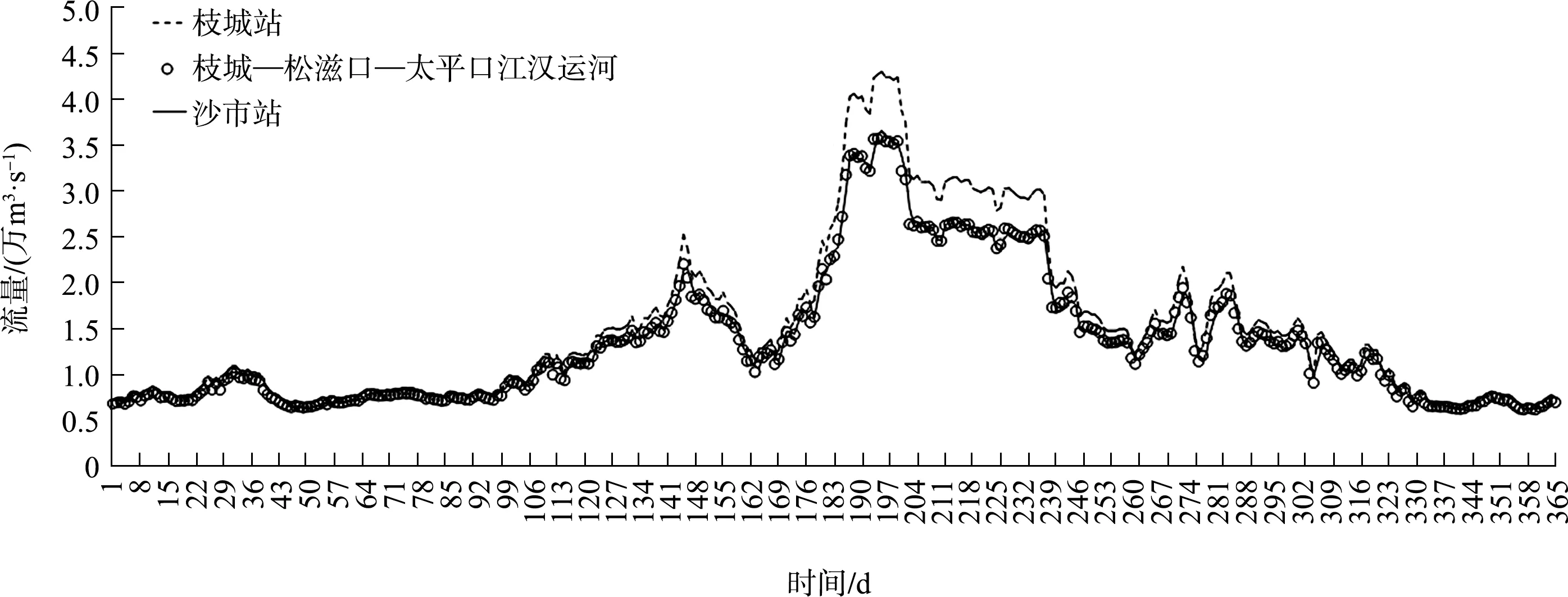
图1 2018 年枝城—沙市站日均流量过程统计

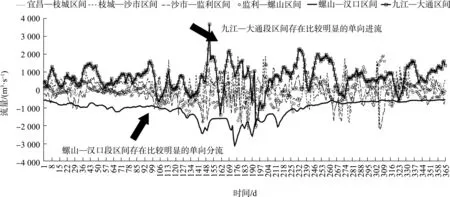
图2 2018 年各水文站点区间流量差值统计

1.2 大通—浏河口河段

大通站以下较大的入江支流，北岸主要有裕溪河、滁河、淮河等，南岸主要有青弋江、水阳江、秦淮河以及太湖水系等。近年来长江下游两岸各地在长江干流沿江修建了大量的引排水涵闸，阻断了各支流的天然通江状态。本节以大通站和徐六泾站之间的年内、年际来水量关系分析区间来流特点。大通站与徐六泾站年际年内径流量比较见图3。

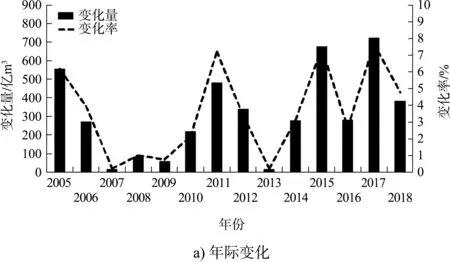
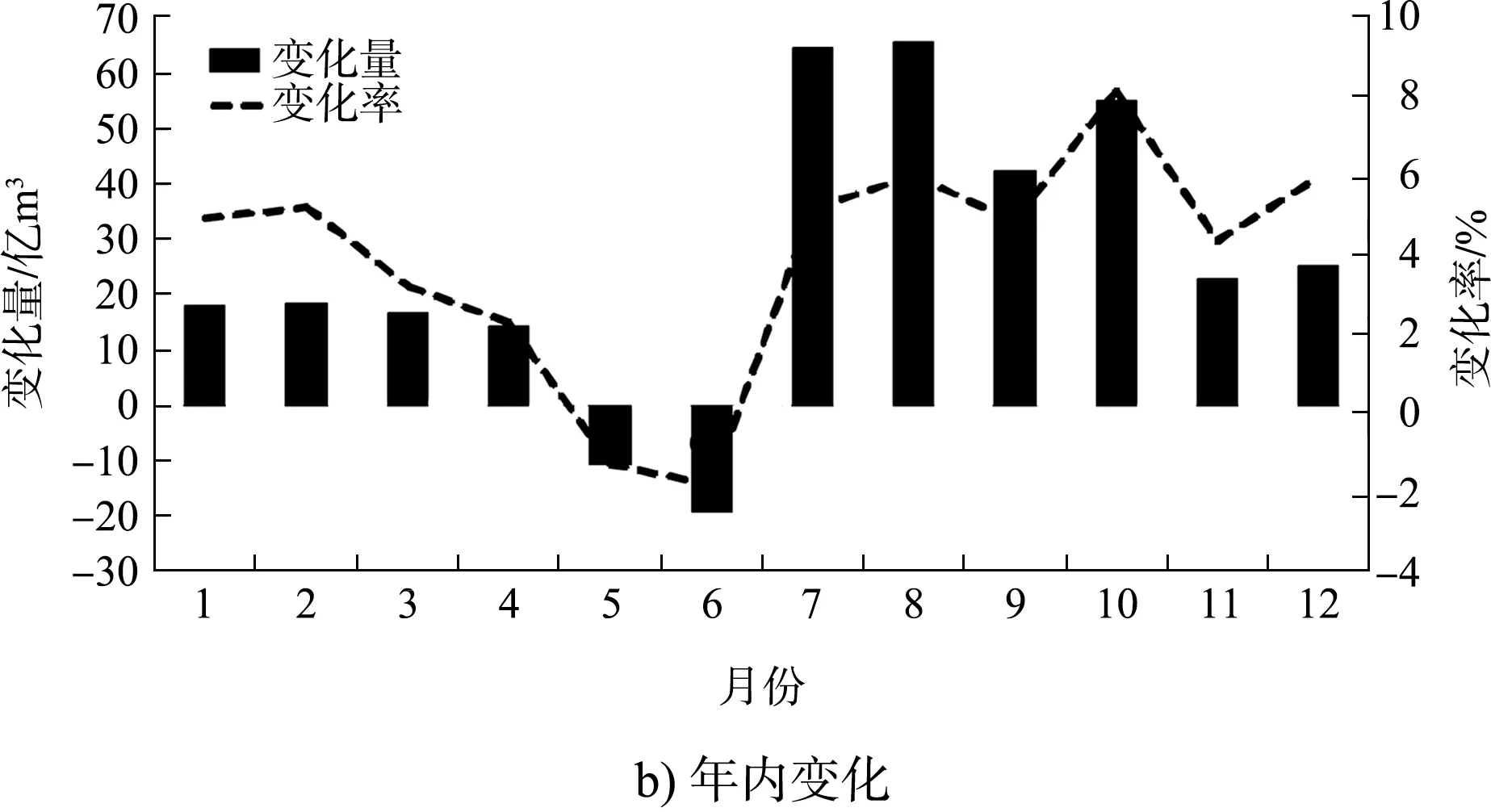
图3 2005—2018 年大通站与徐六泾站区间年际、年内水量变化量及变化率

1.2.1 年际变化

徐六泾站较大通站径流量偏大，历年平均偏大量为313.3 亿m3，平均增幅为3.64%。历年偏大变化率在0.22%～7.70%，增幅最大的为2017 年，增幅最小的为2013 年。两站之间的水量变化主要受沿江通江河流的引排水影响，两站各年的水量变化不一，其中，2005、2015 和2017 年区间水量变化比较大，分别为556 亿、676 亿、722 亿m3，水量变化在500 亿m3以上；2007、2008、2009 和2013 年变化比较小，在100 亿m3以下。

1.2.2 年内变化

历年年内各月只有5 月和6 月这两个月徐六泾站的水量小于大通站，其它各月均是徐六泾站水量大于大通站；其中，两站区间水量变化最大的是主汛期8 月，水量变化量达65.6 亿m3；各月水量变化率最大的为10 月，变化率为8.16%。

综上，宜昌—大通河段应重点考虑螺山—汉口段、九江—大通段的区间未知水源，大通—浏河口河段年内、年际间区间来水量占总量比均小于10%，不需考虑区间未知水源。

2 数学模型建立

2.1 基本控制方程

根据水流的质量和动量守恒定律，建立以面积流量为变量的圣-维南方程组:

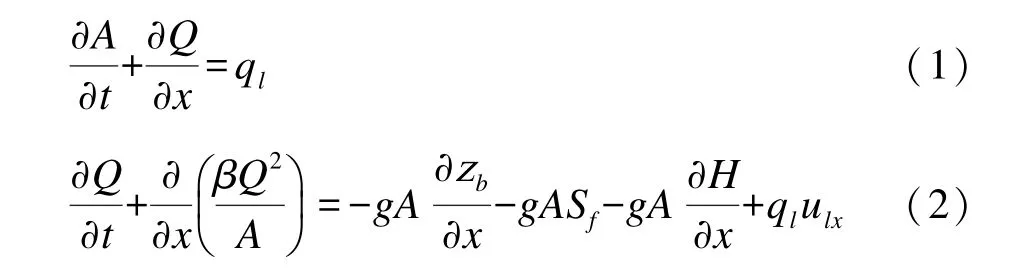
式中:t为时间；x为水流方向；g为重力加速度；A为过水断面面积；Q为流量；zb为河底高程；H为水深；β为动量修正系数；Sf为阻力坡度，为综合糙率，根据Cao 等[5]求解，R为水力半径；ql为旁侧入流的单宽流量；ulx表示单位流程上的侧向出流流速在主流方向的分量。

该方程的水动力学部分较全面地考虑了河道不规则形态、河床与岸坡组成对水流动量通量的影响，并引入动量修正系数β处理。该模型适用于非恒定流，当时间偏导项为零时，退化为恒定流，因此本模型可普遍应用于恒定、非恒定流的计算。

2.2 数值解法

2.2.1 数值离散

为求解方程(1)(2)，采用Cao 等提出的数值解法，即首先对方程进行算子分裂，再采用有限体积SLIC 数值计算格式求解双曲型方程组。方程(1)(2)可以写成矩阵形式:

式中:U为变量矩阵；F为通量矩阵；Sb为除阻力项的源项矩阵；Sd为阻力的源项矩阵。

采用算子分裂分别对方程(3)进行离散，其中除阻力项的源项矩阵Sb采用二阶龙格库塔法计算源项，阻力的源项矩阵Sd采用全隐格式求解。

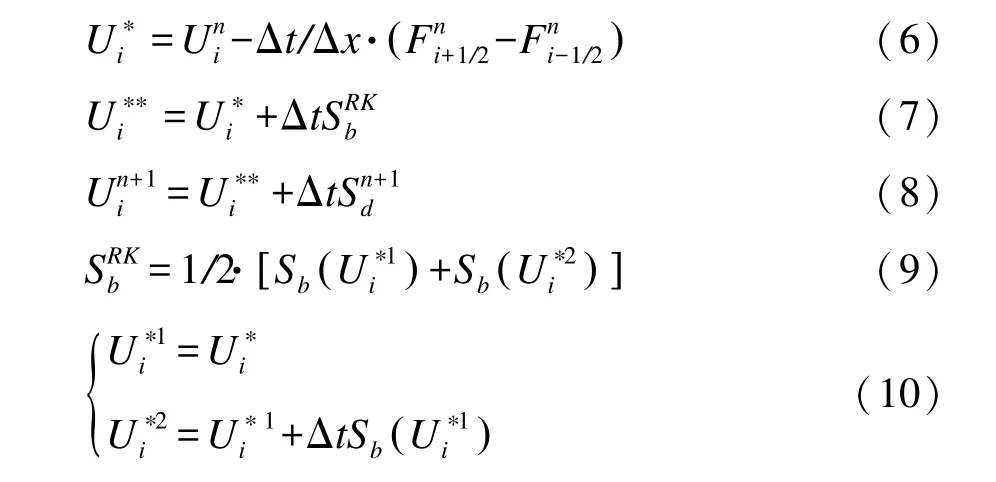
式中:Δt为时间步长；Δx为空间步长；i为空间节点；n为时间节点；Fi＋1∕2和Fi-1∕2为有限体积的SLIC数值格式求解的交界面通量；U**、U*为中间变量矩阵。对于公式(8)中的阻力源项矩阵Sd采用全隐格式[6]，该方法能够处理在小水深条件下由于阻力过大引起的数值震荡，提高计算的稳定性。

2.2.2 通量计算

在计算Fi-1∕2、Fi＋1∕2相邻单元交界面上的通量时，采用SLIC 的数值格式求解，该数值格式方法能够捕捉激波，自动处理部分河段出现急流的情况，同时亦可适用于恒定流的求解计算。该方法分为3 个步骤:

1)第一步数据重构。为避免寄生振荡，在数据重构时采用limited slopes作为约束条件。在相邻单元Ii＝[xi-1∕2，xi＋1∕2]、Ii＋1＝[xi＋1∕2，xi＋3∕2]中，已知位于时间节点n和空间节点i-1、i、i＋1 和i＋2 的变量可以得到

当系数α＝1 时模拟最小限制通量，当系数α＝2时模拟最大限制通量，本项目中取α＝1。则对空间上进行数据重构，上标R，L 分别代表i节点左右两侧:

2)第二步数据重构。在每个单元Ii上，取时间t＝1∕2·Δt，对时间上进行数据重构得

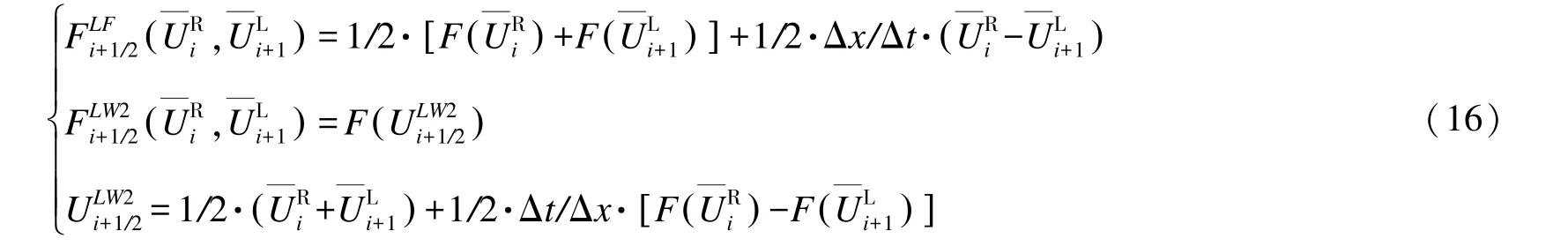
因此可求出相邻单元交界面的通量Fi＋1∕2，代入式(6)进行求解，即可求出下一步各变量的值。

为了使计算稳定，对于显格式时间步长需要满足克朗条件:

即克朗数Cr＜1，λmax为由雅格比矩阵求得的最大特征值。

2.3 河网计算

与基于三级联解算法的有限差分法不同，本文以控制体积为计算单元，实质上不需要对汊道进行额外处理，对于复杂河网也不用进行复杂系数矩阵的求解，程序即可实现自动对存在支流的河段进行水力要素的计算。

如图4，对于由abcd组成的第i点的计算控制体单元Ii＝[xi-1∕2，xi＋1∕2]，从物理上而言，控制体中i节点上n＋1 时刻过流面积等于n时刻该节点上的过流面积加上该时间段内控制体水量的变化量。此时若有支流流入或流出，则支流流量也属于控制体中流入或流出的水量，因此可得到其过流面积及水位值，这可由控制方程的连续性方程中体现出来。同理，控制体中i节点上流量的变化，也可以根据其动量守恒过程，考虑支流水流流入在水流方向上的投影对控制体动量的贡献，从而可得到n＋1 时刻i节点的流量。

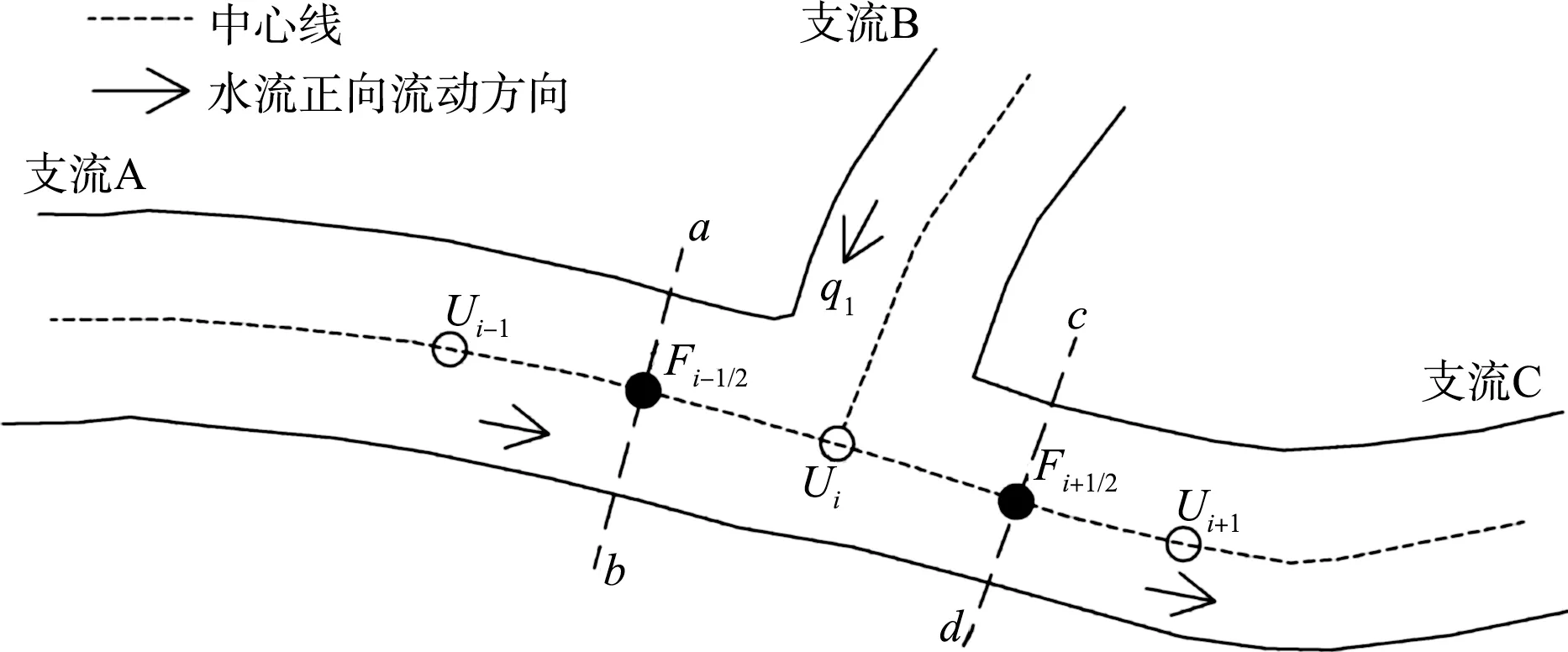
图4 河网计算单元概化

在模型计算时，只需要输入河段中支流的位置及其流入或流出的流量大小和流速方向，即可对有支流的情况进行求解，该求解过程与没有支流时一致，因此并不需要额外增加节点导致增加计算量。

3 模型应用

3.1 河道概化

本文研究的模拟河道概化范围见图5，上起宜昌水文站、下至浏河口(航道里程25.3 km)，包含汉江、北支两条主要支流。由于河段较长，以经度带为界，按石首、九江、安庆节点将长江干线划分为4 个主干河段，其余分汊、支流河道以相互连接方式并入主干河段，进而形成完整的一维河网。模型对河网的26 条水道进行间距800～3 000 m的断面剖分，共剖分出1 128 条断面。模型外部边界上游为宜昌站、仙桃站流量，下游为浏河口附近的杨林站、北支的连兴港站潮位，支流清江入汇采用高坝洲同期实测逐日流量过程，松滋口、太平口、藕池口三口分流分别采用新江口、沙道观、弥陀寺、藕池(康、管)同期实测逐日流量过程，洞庭湖、鄱阳湖入汇采用城陵矶、湖口水文站实测逐日流量过程，江汉运河分流采用引江济汉工程渠道设计流量固定值，螺山—汉口段分流、九江—大通段汇流采用前述区间水量平衡计算成果在区间水域沿线以线源方式设置相应补充水量过程，合计设置了15 处边界条件。模型验证起算地形以2018 年实测地形为主。

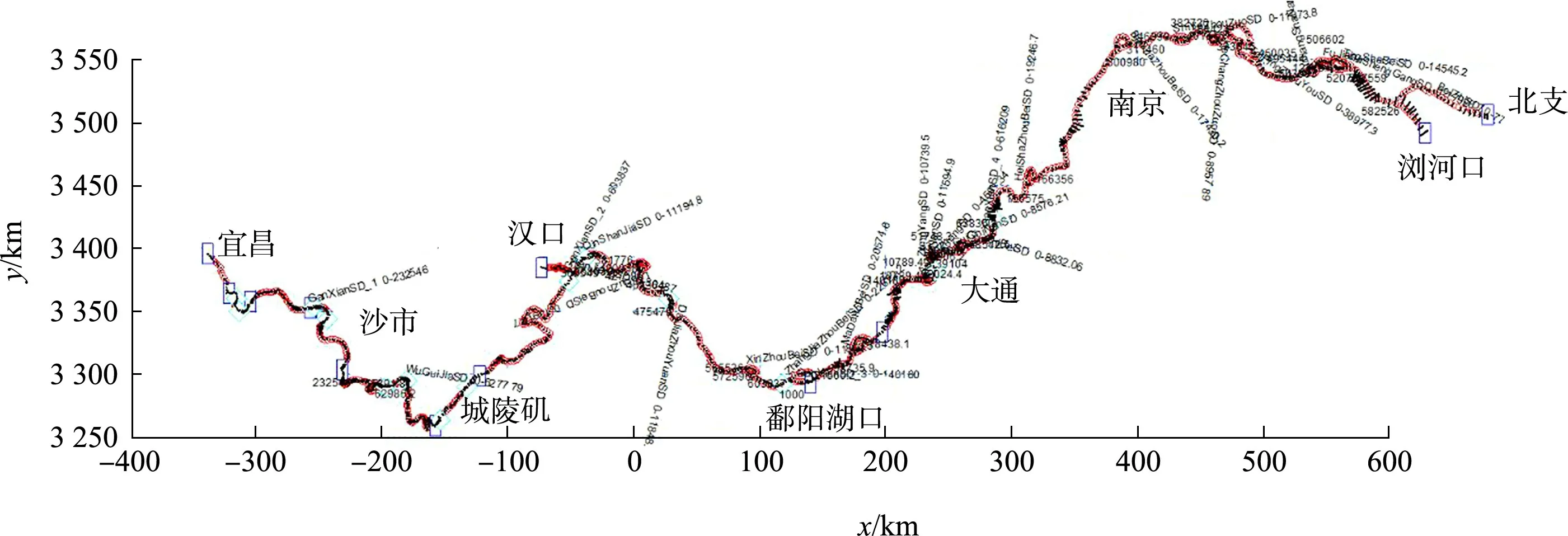
图5 长江宜昌至浏河口段一维河网全局布置

3.2 参数率定

本模型主要根据水位对模型中的综合糙率系数进行率定。根据文献资料搜集沿程河床泥沙组成特性，同时考虑到对于同一断面的非恒定流过程其糙率与水位的关系并非单一，会受到涨水和退水、人工建筑物等影响。通过与枝城、监利、螺山、汉口、黄石港、九江、彭泽和大通等站实测水位数据的对比，率定成果见表2。

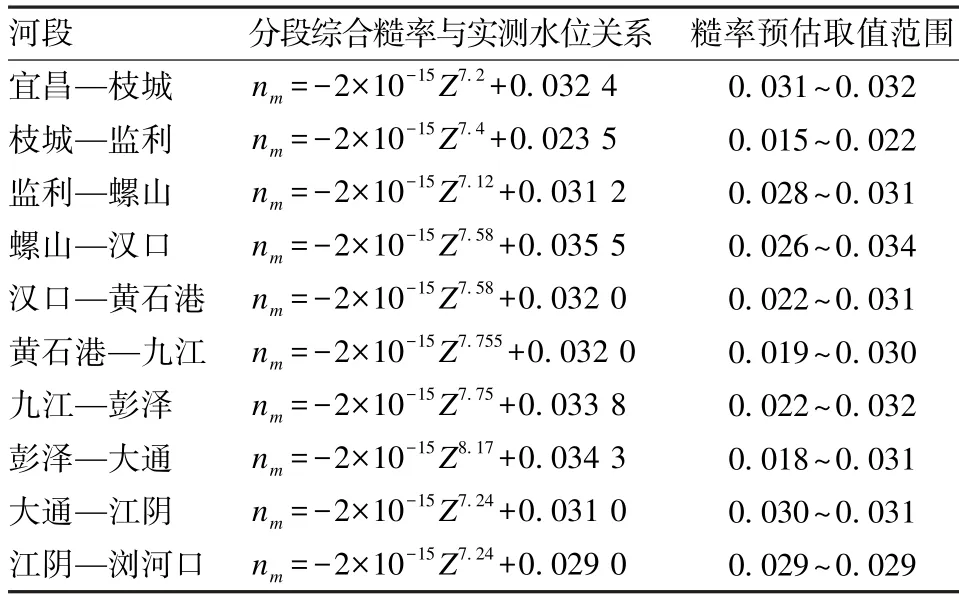
表2 宜昌—浏河口段沿程综合糙率验证取值

3.3 验证成果

长江干线为非恒定流，传统工程上应用的一维模型通常将非恒定水流过程梯级化，每个梯级用恒定流模型计算，这种方法与直接采用非恒定流模型的计算结果差异仍然不是十分清楚。本模型直接采用非恒定模型计算，无需将非恒定来流过程概化为分级恒定流，从物理上减少了模型计算误差，提高了模型精度。值得注意的是，在本模型中，当非恒定流模型的时间偏导项为零时，模型将退化为恒定流模型，同样也适用于恒定水流过程的计算，因此模型具有良好的通用性；由于模型的数值计算方法使其具备了能够自动捕捉激波和处理小水深的能力，对于长江干线局部的急流或急缓流交界的情况，能够自行进行计算并保证模型计算的稳定性。

从模型过程验证(图6)可以看出:长江干线枯、洪期分界明显，年内最高水位一般在7 月中旬，水位与流量成正比关系；大通及以上径流河段实测水位与计算水位之间误差均在10 cm 以内，误差分布较均匀，大通站计算值在枯水期偏低、洪水期偏高；大通以下潮流河段徐六泾站在枯水期2018-02-22T00∶00—2018-02-28T23∶00 时的高低潮位计算误差均在10 cm 以内、相位差为0 h，误差分布较均匀；流量实测值与计算值走势基本一致，两者相对误差在10%以内。因此，本次研究建立的新型一维河网数学模型计算稳定性强、精度较高，能较好地模拟超长网状河段的水动力情况。

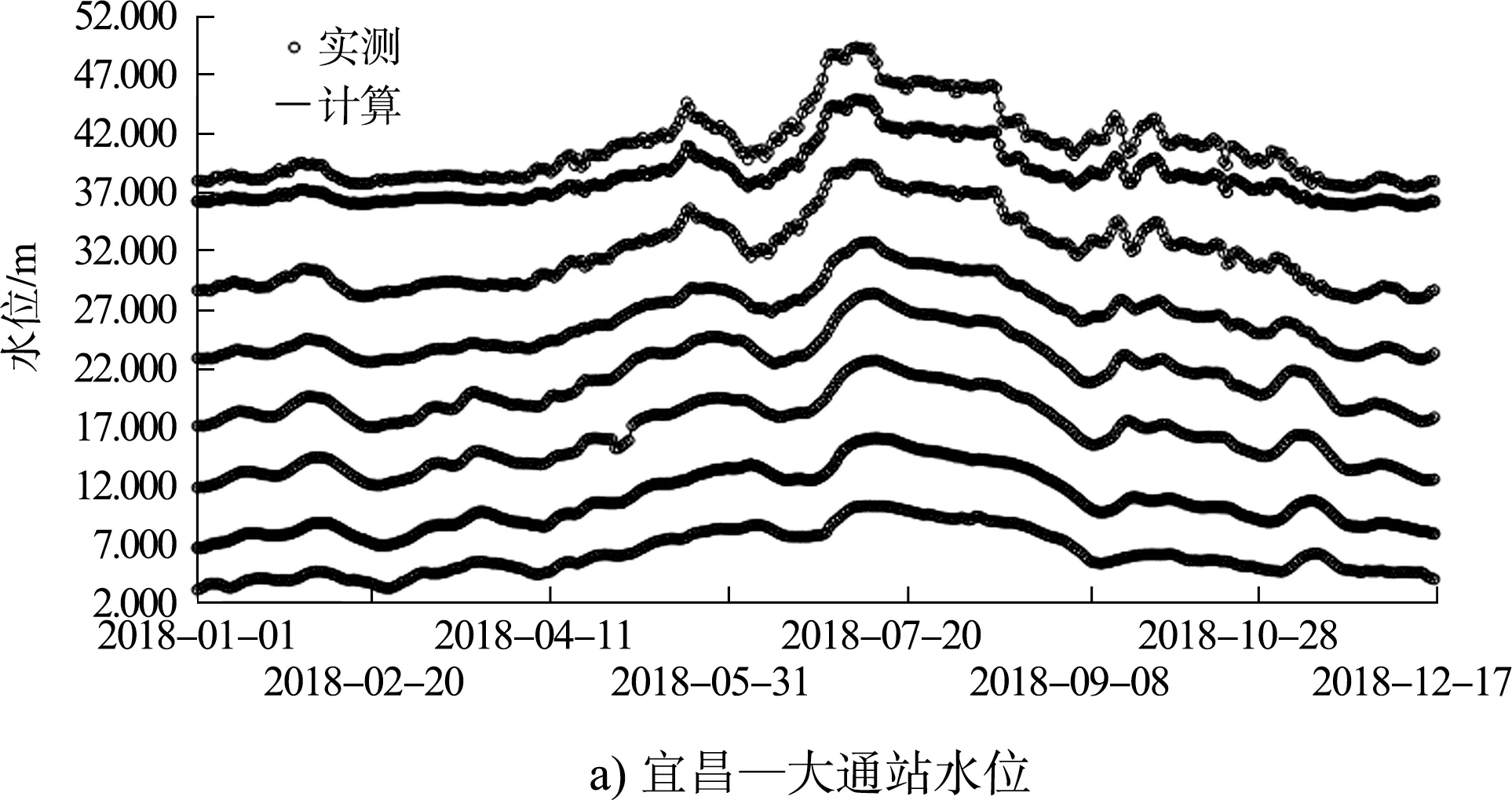
图6 2018 年主要站点水位、潮位、流量过程验证

4 结论

1)自主研发了基于有限体积法离散控制方程的一维河网水流数学模型，采用具有TVD 特性的SLIC 格式计算数值通量，在处理河网交汇方面以控制体为计算单元，可对存在支流的河段进行水力要素的自动快速计算，避免了传统河网计算中对复杂系数矩阵的求解，提高了计算精度。模型可适用于恒定和非恒定流、自动处理急缓流交界处和小水深条件下的水流计算问题，能保证模型计算稳定性，具有较为广泛的应用前景。

2)2018 年宜昌—浏河口段区间来流计算结果表明应重点考虑螺山—汉口段、九江—大通段的区间未知水源，其余区段可暂不考虑。将建立的一维河网模型应用于该河段，计算结果表明:水位流量计算值与实测值基本吻合，能较准确反映超长河网复杂非恒定河道的水动力情况，模型具有较高的模拟精度。