基于管道模型理论的长白落叶松叶生物量与径向生长关系研究

潘 磊，王轶夫，孙 钊，乔晶晶，邱思玉，孙玉军

(北京林业大学森林资源和环境管理国家林业和草原局重点开放性实验室，北京 100083)

叶生物量与光截获、蒸腾作用、光合作用直接相关，是决定树木生产力的最重要因素，为了间接估测叶生物量，Shinozaki 等提出了一种理论框架[1]：管道模型理论（pipe model theory），管道模型认为，在植物体内，单位数量的管道支持单位数量的叶子，管道不仅具有固定的横截面积，而且通过所有的胞间层从叶子通过树枝、树干伸展到根尖部位，许多这样的管道集合成束，形成一棵完整的树形[2-4]。

根据管道模型理论，给定树种的叶生物量应该与树冠基部的树干横断面积成一定比例[1,5]，一些研究已经证明日本扁柏（Chamaecyparis obtusa（Siebold &Zucc.）Endl.）[6-7]、欧洲赤松（Pinus sylvestrisLinn.）[8]、白 桦（Betula platyphyllaSukaczev）[9]的叶生物量与枝下高树干横断面积成比例。另外有研究表明，叶面积与树干边材面积成比例[10]，然而这种比例并非是通用的，也有一些树种存在例外[11-13]，管道模型理论对于长白落叶松（Larix olgensisHenry）是否适用，是一个值得研究的问题。对于单株林木而言，关于树叶在树冠内的分布，先前的一些研究一般认为树叶的分布在不同方向间没有差异[14-16]，然而在实地调查中发现，树冠半径和树叶的分布在不同方向是有差异的。一些研究表明，分支大小和光合作用特征在不同水平方位是存在差异的，这种差异可能是由光环境的差异和不同方向竞争压力大小的差异造成的[17-18]。

在树干解析的过程中，发现树干半径和径向生长量在不同方向上也存在差异，树冠偏冠与树干髓心偏心是生物量在树冠和树干上的不均匀分布，结合管道模型理论分析单木株内树冠生物量在不同方位的不均匀分布与径向生长周向变异的关系，有助于理解树干生长和树冠结构之间的功能关系，对于理解树木生长发育等生态过程具有重要的意义。

1 研究方法与材料

1.1 叶生物量测定

1.1.1 单木叶生物量测定 将解析木伐倒后，使用分层标准枝法按1 m 分层对标准木的叶生物量进行了测定。测定时，首先按1 m 对树干进行分段，使用手锯和枝剪将每段的枝条沿基部截下，现场使用电子秤称取每个枝条的带叶鲜质量，结合每段的平均枝长、平均基径和平均鲜质量，在每段选取2～3 个标准枝，称量其带叶鲜质量，然后将标准枝上的枝与叶分离，并分别称取枝和叶鲜质量，而后均匀选取50 g 左右的叶样本，记录叶样本的鲜质量，将叶样本带回至实验室，置于烘箱中在105 ℃恒温下烘干2 天左右至恒质量，称取记录每个叶样本的干质量即生物量，计算叶样本的含水量，根据现场测定的每层叶鲜质量和该层叶样本的含水率，计算每层的叶生物量，累加后即为该株解析木的叶生物量。

本研究在黑龙江省伊春市朗乡林业局东折棱河林场共调查获取了31 株不同林龄的长白落叶松解析木的叶生物量数据和径向生长量数据，其基本统计指标如表1 所示。

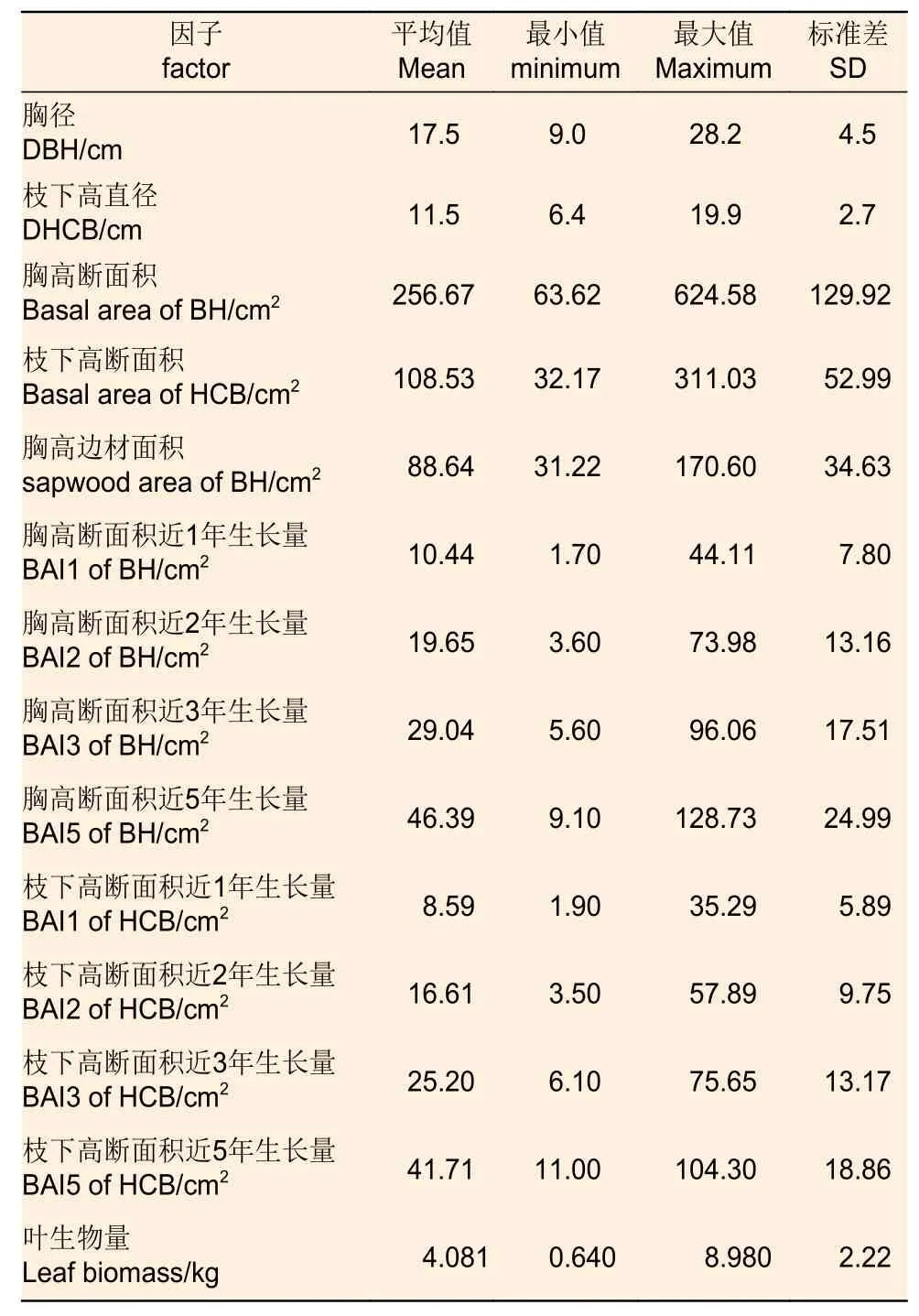
表1 建模生物量解析木的基本统计量Table 1 Descriptive statistics of sampled trees for biomass equations development

1.1.2 株内不同方位叶生物量测定 在单木株内水平上，将树冠以45°间隔分为北(337.5°,22.5°)、东 北(22.5°,67.5°)、东(67.5°,112.5°)、东南(112.5°,157.5°)、南(157.5°,202.5°)、西南(202.5°,247.5°)、西 (247.5°,292.5°)、西 北(292.5°,337.5°) 8 个水平区间。

对标准木进行叶生物量测定时，使用数显角度尺，以正北为0°，量测每个枝条的方位角，在各个区分段内，分别对8 个水平区间所有枝条进行称质量。分别选取标准枝，将标准枝上的树叶全部剥离称质量，计算标准枝上树叶的所占比例，而后收集50 g 左右的鲜叶样品，将鲜叶样本带回至实验室，置于烘箱中在105 ℃恒温下烘干2 天左右至恒质量，称取记录每个叶样本的干质量即生物量，计算叶样本的含水量。根据各个区间的树枝总质量、树叶鲜质量占树枝鲜质量比例、树叶含水率，计算标准木各个方位区间的叶生物量。因为该项工作量较大，只对10 株解析木进行了株内不同方位的叶生物量调查，基本信息如表2 所示。

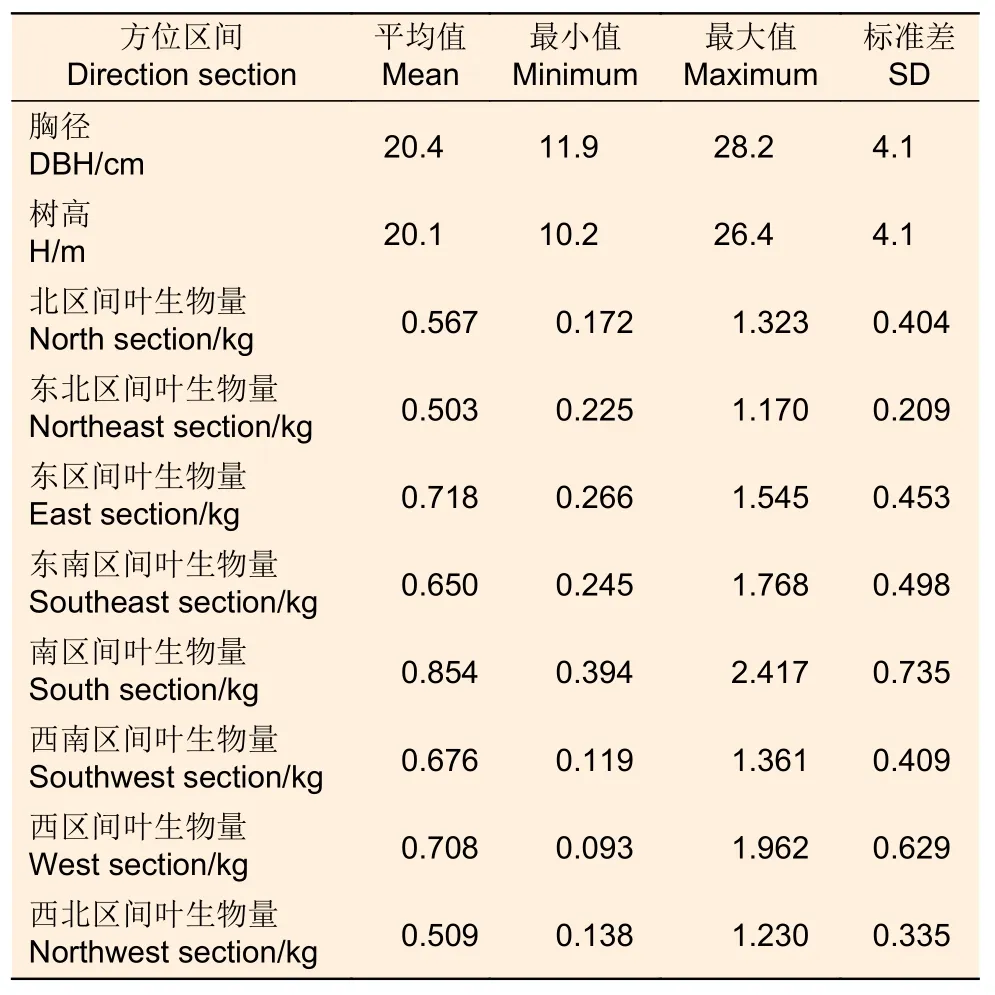
表2 株内不同方位区间的叶生物量Table 2 Descriptive statistics of sampled trees for leaf biomass in different direction

1.2 径向生长测量

将标准木伐倒后，截取胸高处和枝下高处的圆盘，并在工作面上表明正北方向，将圆盘带回实验室，使用角磨机和砂纸将圆盘工作面打磨抛光至年轮清晰可见，并在工作面上使用铅笔标明北、东北、东、东南、南、西南、西、西北8 个方向，而后将圆盘放在扫描仪上使用1200dpi 的分辨率扫描成jpg 格式的栅格图像，利用WinDENDRO 年轮分析系统测定圆盘上8 个方向树干半径上的年轮宽度，测定精度为0.01 mm，以此获得圆盘上8 个树干半径的长度和各个方向上的年轮宽度。

分别以8 个方向上的树干半径为半径计算1/8的圆面积，将8 个树干半径计算的1/8 圆面积的和视为该高度的树干断面积。与上述10 株解析木不同方位区间叶生物量对应的不同方位区间树干半径、断面积和断面积生长量的基本信息如表3 所示。

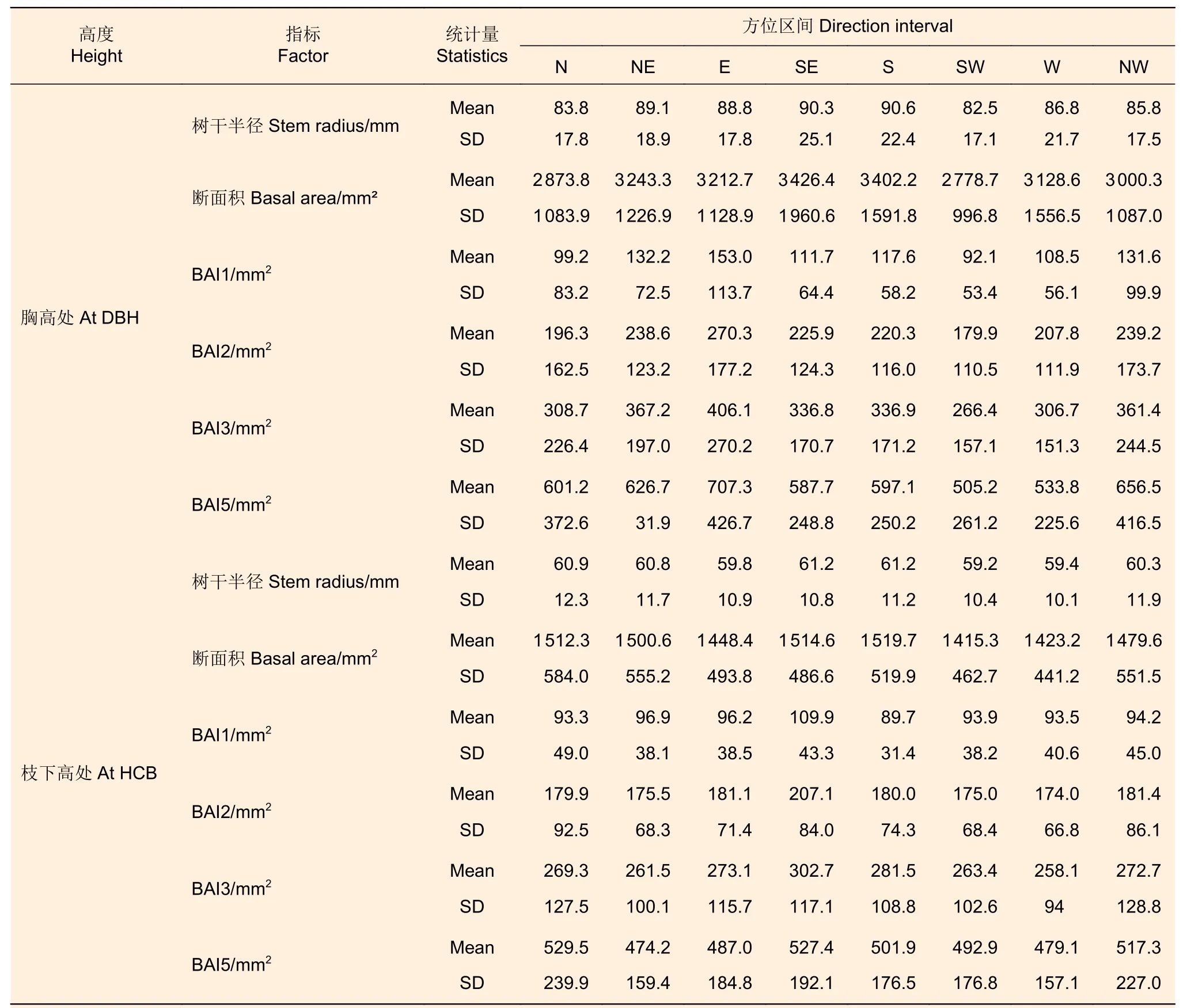
表3 株内不同方位区间的断面积及生长量Table 3 Basal area and increment of different directions within tree

在胸高处圆盘上以颜色区分出心材和边材的界限，分别量测8 个方向上的心材半径，使用上述计算树干断面积的方法，分别计算得出8 个区间的心材面积，使用各个方向上对应的树干断面积减去心材面积，即得出各个方向上的边材面积，将8 个方向上的边材面积相加即为胸高处边材面积，由于在枝下高处圆盘上心材和边材的颜色界限不明显，不能根据颜色进行辨别，故只对胸高处的边材面积进行了测量计算。

1.3 统计分析

结合管道模型理论，使用一元线性回归模型分析了胸高处和枝下高处的直径、断面积、胸高边材面积和近n年断面积生长量的关系；由于树木存在树冠偏冠和树干髓心偏心现象，为了探讨这两种现象是否存在关系，结合管道模型理论，分别以长白落叶松株内不同方位区间的叶生物量和对应方向区间的胸高处和枝下高处的树干半径、断面积和断面积近n年生长量进行相关分析。数据处理分析、图形绘制均在R 3.6.5 中进行。

调查的上海环城绿带植物群落的乔木层的 Shannon-Wiener 指数在 0～1.572之间,平均为0.750。群落的物种多样性指数整体偏小,乔灌草各层物种多样性变化没有明显规律,不同群落间的物种多样性有明显差异。该结果反映出百米林带植物群落在最初进行设计时,对群落的生态效应和稳定性未作充分考虑,从而表现出群落丰富度不够。

2 结果与分析

2.1 单木叶生物量与径向生长的关系

2.1.1 单木叶生物量与树干直径的关系 根据管道模型理论的基本原理，单株树木的叶生物量与树干断面积成一定比例关系。本研究绘制了单木叶生物量与胸径、胸高断面积、枝下高直径、枝下高断面积的散点图，并根据散点分布趋势和生物量原理建立了y=ax的线性关系（图1、图2）。

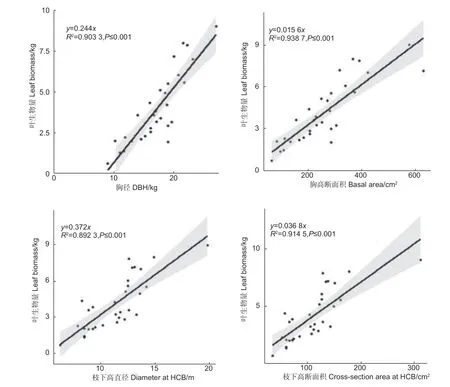
图1 单株叶生物量与直径、断面积的关系Fig.1 The relationship between leaf biomass and diameter and basal area

由图1 可知，单木胸径和胸高断面积与单木叶生物量均成明显的线性关系，两者的决定系数均达到了0.90 以上，其中胸高断面积的决定系数略高于胸径的决定系数。单木枝下高直径和枝下高断面积与单木叶生物量同样均成明显的线性关系，两者的决定系数均达到了0.89 以上，其中枝下高断面积的决定系数略高于枝下高直径的决定系数。

由图2 可知，胸高边材面积与叶生物量也呈现明显的线性关系，其决定系数达到0.863 5，说明胸高边材与叶生物量存在较好的相关性，不过略低于胸径、胸高断面积、枝下高直径、枝下高断面积的决定系数。本研究中边材是通过颜色差异和心材进行区别的，可能会存在测量误差。根据管道模型理论，树干中任何部位的边材均应与其上方的叶生物量具有良好的相关关系，该结果符合管道模型理论。

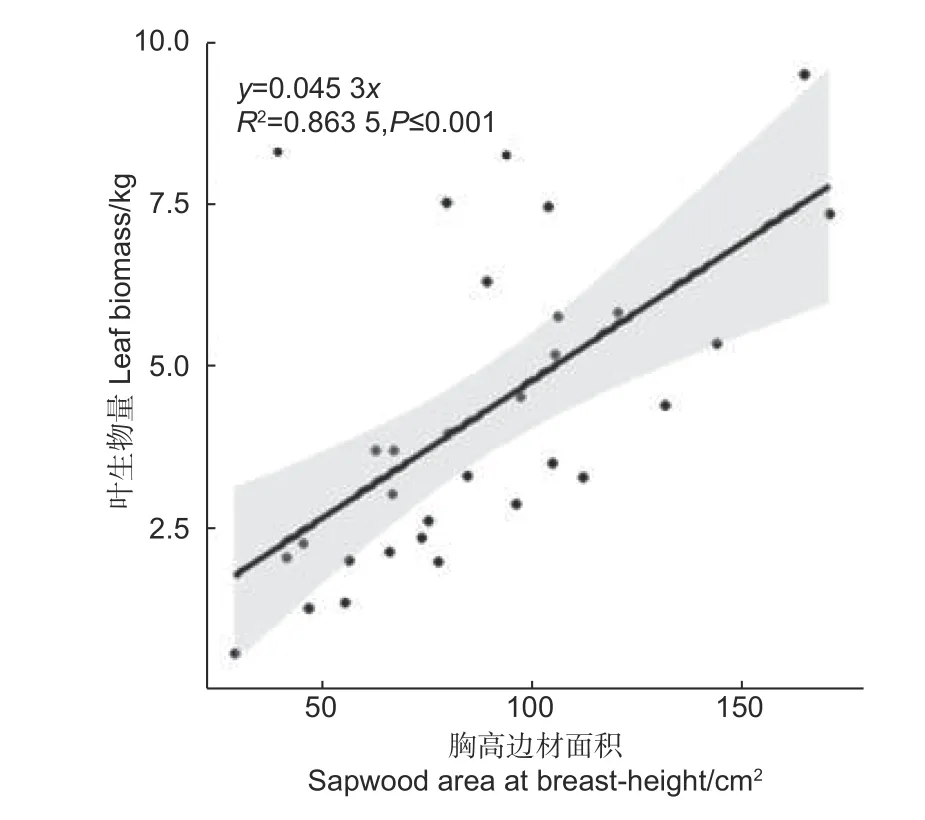
图2 单株叶生物量与胸高边材面积的关系Fig.2 The relationship between leaf biomass and sapwood basal area at breast height

2.1.2 单木叶生物量与树干断面积生长量的关系

对于单木而言，树叶与树干是相互依赖，相互制约的，叶量的多少受到树干运输水分和矿物质能力大小的制约，树干的生长快慢又受到树叶光合作用合成有机物多少的制约[19]。而在树干中，只有边材部分具有输导能力，然而边材与心材的分别一般以颜色来区分，在颜色不明显时，在边材与心材的交界处可能存在辨别误差，并且有学者表明，对于针叶树而言，边材部分靠近心材的部分年轮已不再具备输导能力，树干最外围的一两个年轮起到的输导作用最大[20]。为此，本研究建立了叶生物量与胸高处、枝下高处最近1，2，3，5 年断面积生长量之间y=a+bx的线性关系（如图3）。

由图3 可知，胸高断面积近1、2、3、5 年生长量均与叶生物量呈显著正相关，决定系数在0.64和0.79 之间，其中近5 年生长量的决定系数最大为0.786 1，然后依次是近3 年生长量（0.744 5），近2 年生长量（0.704 5），近1 年生长量（0.646 2）。枝下高断面积近1、2、3、5 年生长量也均与叶生物量呈显著正相关，决定系数在0.72 和0.78 之间，其中近5 年生长量的决定系数最大为0.784 1，然后依次是近3 年生长量（0.755 3），近2 年生长量（0.733 7），近1 年生长量（0.720 1），略高于胸高处断面积生长量的决定系数。

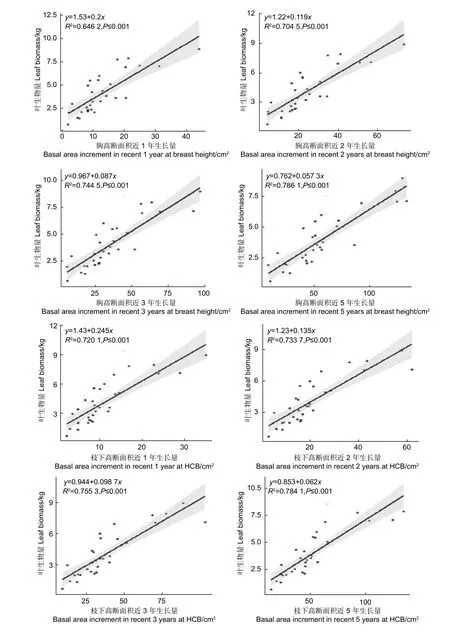
图3 单株叶生物量与胸高、枝下高断面积近1 年、2 年、3 年、5 年生长量的关系Fig.3 The relationship between leaf biomass and basal area increment in recent 1, 2, 3, 5 years at breast height and height to crown base

2.2 株内不同方位叶生物量与径向生长的关系

由表4 可知，株内不同方位叶生物量与胸高处和枝下高处的半径、断面积和近1、2、3、5 年断面积生长量均呈显著正相关。总体而言，对应方位树干半径、断面积的相关系数要高于近1、2、3、5 年断面积生长量的相关系数。枝下高处树干半径、断面积的相关系数要高于胸高处的，而对于断面积生长量而言，胸高处的相关系数均高于枝下高处的相关系数。

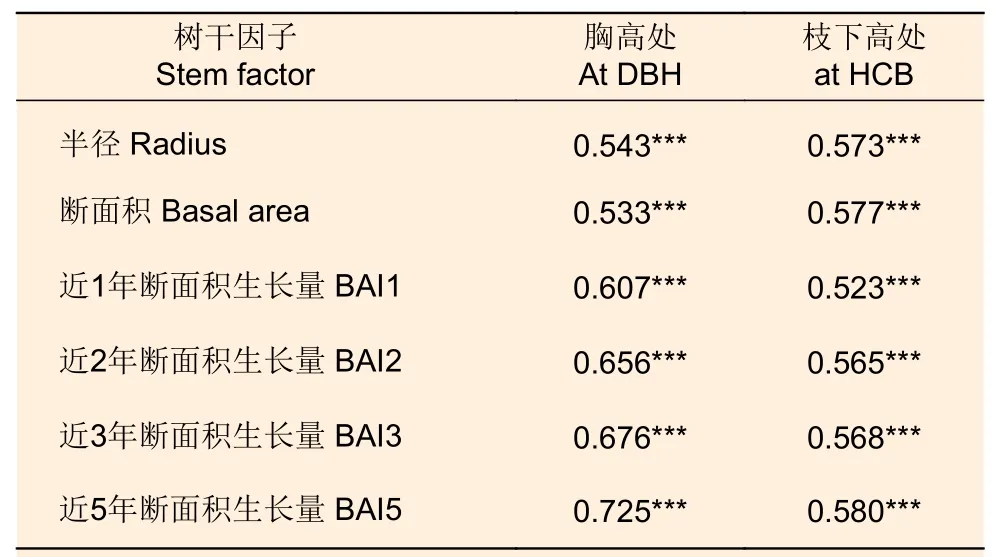
表4 株内不同方位叶生物量与对应方位树干半径、断面积和断面积生长量的相关系数Table 4 Correlation coefficients between leaf biomass in different directions and stem radius, basal area and basal area increment in corresponding directions

2.2.1 不同方位区间叶生物量与树干半径的关系

由图4 可知，不同方位区间胸高半径和胸高断面积与对应方位区间的叶生物量均成明显的线性关系，两者的决定系数均达到了0.70 左右，其中胸高断面积的决定系数略高于胸径的决定系数。不同方位区间枝下高半径径和枝下高断面积与对应方位区间叶生物量同样均成明显的线性关系，两者的决定系数均达到了0.70 以上，其中枝下高断面积的决定系数略高于枝下高半径的决定系数。

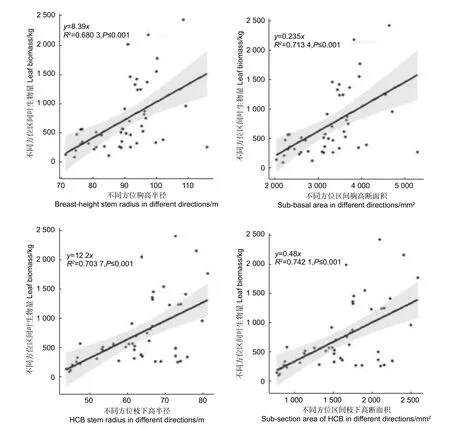
图4 株内不同方位区间叶生物量与对应区间半径、断面积的关系Fig.4 The relationship between leaf biomass and radius and basal area of different orientations

2.2.2 不同方位区间叶生物量与树干断面积生长量的关系 为了探究树冠的叶生物量分布与径向生长量的关系，建立了不同方位区间叶生物量与对应方位区间胸高处、枝下高处最近1，2，3，5 年断面积生长量之间y=a+bx的线性关系（图5）。

由图5 可知，不同方位区间胸高断面积近1、2、3、5 年生长量均与对应区间叶生物量呈显著正相关，决定系数在0.36 和0.52 之间，其中近5 年生长量的决定系数最大为0.525 5，然后依次是近3 年，近2 年，近1 年生长量。不同方位区间枝下高断面积近1、2、3、5 年生长量也均与对应方位区间叶生物量呈显著正相关，决定系数在0.27 和0.34 之间，其中近5 年生长量的决定系数最大为0.335 9，然后依次是近3 年，近2 年，近1 年生长量，低于不同方位区间胸高处断面积生长量与叶生物量的相关关系。

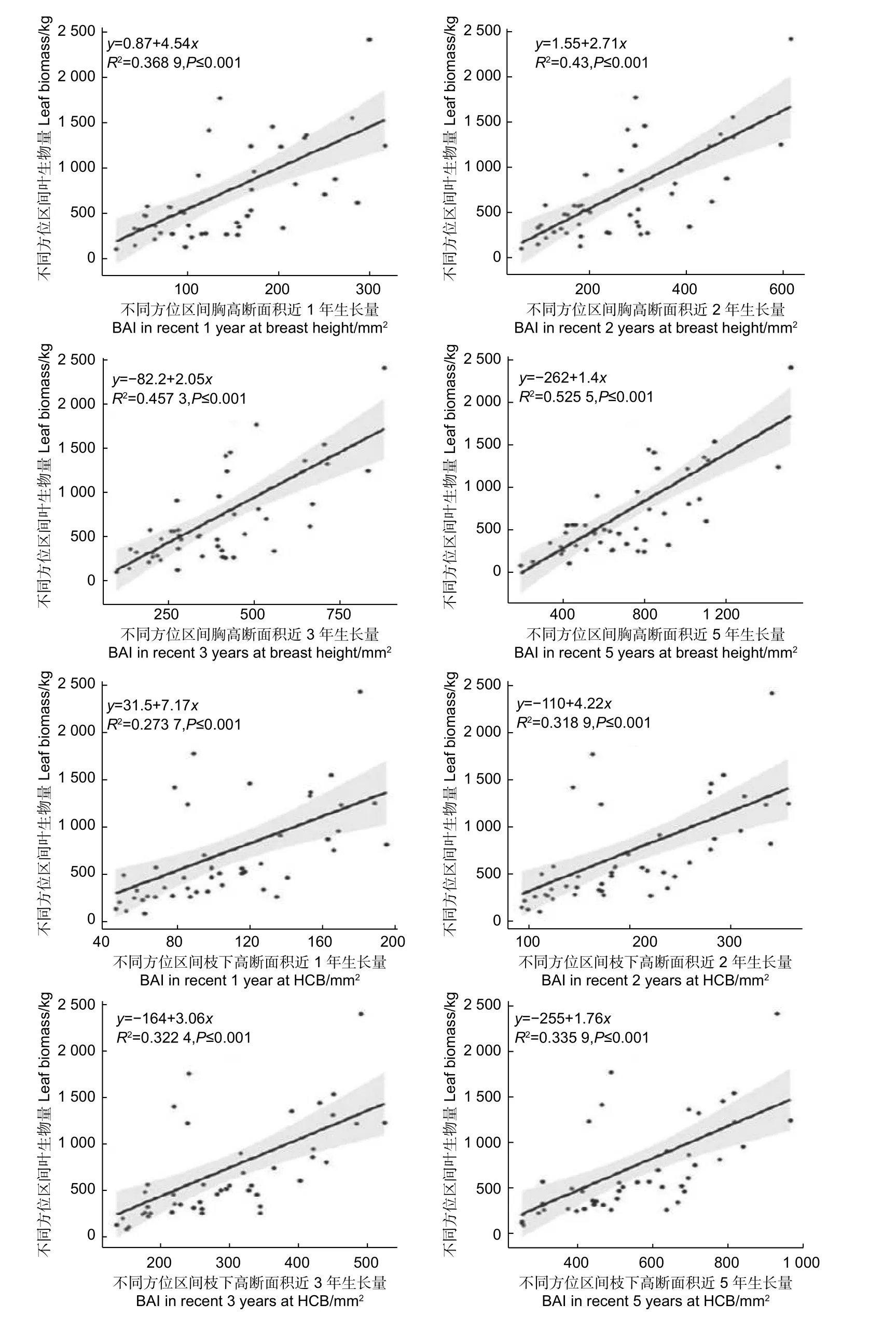
图5 不同方位叶生物量与胸高、枝下高断面积近1，2，3，5 年生长量的关系Fig.5 The relationship between leaf biomass and basal area increment in recent 1, 2, 3, 5 years at breast height and height to crown base

3 讨论

刘盛等[21]使用生物染色剂对长白落叶松的水分输导模式进行了研究，结果表明长白落叶松枝干中的水分输导模式符合管道模型理论，水分在枝干的不同年轮间没有明显的横向输导现象，在同一年轮内，水分的向上传输呈现较好的定向传输性，并不是均衡向上传输，说明某一枝条上的树叶仅与某些导管相连接，从树叶基部通过树干中的导管贯通至根系。

Shinozaki 等[22]在他们关于管道模型理论的第二篇论文中使用实验数据进一步验证了该理论，并得出结论“作为该理论在森林生态学中的应用，根据叶生物量和枝下高树干横截面积之间的比例关系，可以估算树木和林分的叶生物量，”尽管该方法比Joseph[23]提出的使用胸径的方法更精确，但是并未得到广泛使用，有以下几个原因，首先，该比例不仅取决于树种，还取决于生长条件和林木发育阶段，其次，次生生长是一个不可逆的累积过程，树干直径可以增长或停滞，但是不会减少，而树木的叶生物量或叶面积可能会增加或减少，可能会出现季节性波动[24]，或因为竞争、衰老、机械损伤而减少[25]。最后，基于管道模型理论的叶生物量估计需要测量到枝下高处，并在不同方向获取样芯，以推测计算枝下高处的边材面积，而这些测量工作都比只测量胸径要繁琐复杂。一些研究者调查了胸高处边材面积和枝下高处边材面积与胸径和枝下高直径在估测叶生物量上的相关程度，并对结果进行了对比。以胸径范围在13～43 cm，年龄在15～55 a 之间的火炬松为例，使用胸径估测叶生物量的效果等于或优于胸高处边材面积和枝下高处边材面积[26]。Snell and Brown[27]对7 个针叶树种的研究表明，对于其中3 个树种，边材面积对于叶生物量和枝生物量的估测效果要优于胸径，而对于其他4 个树种，边材面积和胸径对于叶生物量的估测效果没有显著差异。因此，可能为了便于野外测量，在大多数研究工作中，树干直径仍然是用来估计叶生物量的首选方法。

树冠形状和叶生物量分布与树干的径向生长紧密相关，并且会影响光合产物在树干中的分布[28-29]，由于叶生物量在周向上的不均匀分布，树干上常常会伴随产生与木材力学性能相关的偏心径向生长[30]。

导致树冠偏冠和叶生物量不均匀分布的一个外因是邻近竞争。在本研究中，长白落叶松不仅存在不同程度的树冠偏冠，在树干中也存在着一定程度的偏心径向生长。通过分析长白落叶松株内不同方位叶生物量与对应方位胸高处和枝下高处半径和径向生长量的关系，结果表明，株内不同方位叶生物量分布与对应方位径向生长量呈显著正相关，也就意味着上方树冠的分布越多，下方树干的径向生长也就越快。较大的冠形意味着更大的树冠生物量和叶生物量，这可能是对应径向生长相较更快的原因[31-32]。

4 结论

本研究基于管道模型理论，使用树冠的叶生物量和树干直径、断面积、断面积生长量等实测数据，在单木水平上拟合了叶生物量估测模型，对比了使用胸高处和枝下高处树干直径、断面积、边材面积和近1、2、3、5 年断面积生长量估测单木叶生物量的效果，结果表明胸高断面积作为预测因子的拟合效果最好。由于树冠偏冠现象和树干髓心偏心现象的存在，基于管道模型理论的扩展，本研究将单木根据方位分为8 个均等区域，分别调查了各区域的叶生物量和对应的胸高处和枝下高处的树干半径、断面积和近1、2、3、5 年断面积生长量，通过与叶生物量的相关分析表明，单木株内不同方位区域的叶生物量与对应的胸径处和枝下高处的树干半径、断面积和近1、2、3、5 年断面积生长量均呈显著正相关。本研究以长白落叶松叶生物量和径向生长相关因子为研究对象，结合管道模型理论，初步分析了长白落叶松偏冠现象与树干髓心偏心现象之间的关系，不过本研究只是进行了初步的统计分析，而未更深层次的结合树木生理学进行研究分析，对树冠偏冠和髓心偏心关系的确定还需今后进一步的研究。