多视角解析一道2021年高考数学文化试题

宋建辉

(福建省福州格致中学 350001)

2021年高考数学全国乙卷理科第9题源自魏晋时期我国数学家刘徽的著作《海岛算经》，试题叙述简洁，阅读顺畅，在考查学生综合运用知识解决问题能力的同时，既宣扬了我国优秀传统文化和古代数学的辉煌成就，又让学生充分感悟到我国古代数学家的聪明才智，彰显了立德树人导向.

1 试题评析

题目 魏晋时期刘徽撰写的《海岛算经》是有关测量的数学著作，其中第一题是测海岛的高.如图，点

E

,

H

,

G

在水平线

AC

上，

DE

和

FG

是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，

EG

称为“表距”，

GC

和

EH

都称为“表目距”，

GC

与

EH

的差称为“表目距的差”，则海岛的高

AB

=( ).

表高

表高

表距

表距

背景分析：《海岛算经》是中国最早的一部运用几何理论解决各种测量难题的数学专著.首题原文如下：

今有望海岛，立两表，齐高三丈，前后相去千步，令后表与前表参相直.从前表却行一百二十三步，人目著地取望岛峰，与表末参合.从后表却行一百二十七步，人目著地取望岛峰，亦与表末参合.问岛高及去表各几何？

答曰：岛高四里五十五步；去表一百二里一百五十步.

术曰：以表高乘表间为实；相多为法，除之.所得加表高，即得岛高.求前表去岛远近者：以前表却行乘表间为实；相多为法.除之，得岛去表数.

文中给出的测量算法(术曰部分)公式用白话文可表述为：

岛高表高，岛去

结合图形，上述结论“翻译”如下：

①，

②.

可以看出，原文给的是确切的已知数，高考试题把已知条件用字母表示，求的是岛高的表达式，属于客观性中等难度试题.笔者了解到大量考生对于本题的基本反应集中于：题目的文字固然简短，但对“表高”“表距”“表目距”“表目距的差”等理解不到位，又基于试题所处的特殊位置及考场的氛围而引发的应试心理状态，部分考生出现了临场思维受阻现象，一时难以将个体认知结构中储备的各种“解题工具”进行有效提取，未能找到合适的比较与化归的突破口，从而使得本题的准确解答率较低，不少考生只能依靠连猜带蒙的方式胡乱选择一个答案，从而影响了本题考查目标的落实.

2 解法探究

我们知道，数学语言可分为抽象性数学语言和直观性数学语言，又可归结为文字语言、符号语言、图形语言三类.因此，在解决问题时，应首先将题目提供的文字语言，结合题目图形转化为符号语言，符号语言指意简明，书写方便，且集中表达数学内容，有助思维，有益于问题解决.因此，应结合图形，首先将题目中的“表高”“表距”“表目距”“表目距的差”等条件转换为符号语言，其次再探究解决问题的方法.

设海岛的高

AB

=

h.

记表高

DE

=

FG

=

d

，表距

EG

=

t

，表目距

GC

=

m

，

EH

=

n

，表目距的差

s

=

m

-

n.

解法1 针对问题及选项的数学结构特征，自然想到应用平面几何有关知识加以解决.

因为

AB

∥

DE

，

AB

∥

FG

，所以即所以又

AC

-

AH

=

HC

=

HG

+

GC

=

EG

-

EH

+

GC

=

t

+

s

，

所以即所以表高，选A.

评析 我们看到，所使用的工具都是利用垂直关系所连接起来的测竿(表高)，其数据来自利用两次或多次测望所得，推算过程仅涉及到初中平面几何知识：平行线分线段成比例定理，在用符号语言表述后，试题解决流畅、自然.

基于解法1仅涉及初中平面几何知识，根据选项的结构特征，亦可考虑利用面积思想来解决问题，于是便有以下的“创新”解法.

解法2 面积思想

如下图，把原图补充成矩形，得到四块不同的区域，其面积分别记为

S

,

S

,

S

,

S

.

根据矩形的对角线平分面积，可得

所以表高，选A.

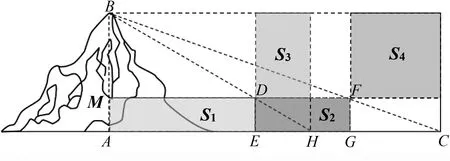
评析 虽然该解法有点“标新立异”，但是解法不落俗套，体现了思维的灵活性，展示了“数学建模”的核心素养.

我们知道，在中学数学教材中，测量不可及物高度与距离问题是解三角形的常见实际问题类型之一.本题的测海岛的高与人教A版必修第二册第50页例10源出一辙，应用三角函数及解三角形知识也能快速便捷地解决问题.

解法3 三角法

如图，连结

DF

交

AB

于

M

，则

AB

=

AM

+

BM.

记∠

BDM

=

α

,∠

BFM

=

β

，则而所以从而所以表高.

评析 三角函数是沟通边角关系的一座桥梁，解法3充分体现了测量问题中三角函数相关知识的巨大作用.刘徽时代还没有出现三角函数理论，三角学传入中国已是17世纪的事了，前后相差约1400年，因此刘徽建立不可及物高度与距离的测量算法公式，展现出他高超的数学智慧.

3 反思

刘徽及其数学著作是中国古代数学成就的杰出代表，我国著名数学家吴文俊先生在《〈九章算术〉及其刘徽注研究》序中指出：“肇始于我国的这种机械化(算法)体系，在经过明代以来近几百年的相对消沉后，由于计算机的出现，已越来越为数学家所认识与重视，势将重新登上历史舞台”.海岛高度的测量算法(术)充分体现了《九章算术》的宗旨“析理以辞，解题用图”，该宗旨促进了我国数学机械化算法体系的构建，这与当今计算数学的一个重点研究方向“找到高效算法”高度吻合，因此该题的考查意义与教育价值不言而喻，而上述3种解法就是在探索“不可及物高度的测量”算法，其中解法3更具有普适性，是一种高效算法.

近年来在高考中出现了大量关注传统文化的优秀试题，它对“数学文化融入课程内容”起到了正确导向的作用，指导着我们在教学活动中，要善于挖掘、提炼传统文化资源，“润物细无声”般地在教与学中感受传统文化的价值，唤醒隐藏心底的数学文化意识，进而增进学生学习数学的情感，促进学生数学核心素养的全面提升.