黄土地层基坑开挖对既有地铁隧道影响分析

王立新， 徐硕硕， 王俊， 施王帅胤， 余德强， 邱军领， 范飞飞

(1.中铁第一勘察设计院集团有限公司, 西安 710043; 2.西安理工大学土木建筑工程学院， 西安 710048； 3.长安大学公路学院, 西安 710064; 4.陕西省土地工程建设集团, 西安 710065)

社会经济的飞速发展推动了城市化进程不断向前，城市轨道交通网线变得更加密集，截至2020年末，中国先后有43座城市开通地铁，总里程达6 645 km，城市轨道交通在未来城市发展中占据愈加重要的地位。但由于城市地铁在规划建设初期无法充分考虑到后续城市规划建设问题，导致出现了越来越多近接既有地铁隧道的工程，地铁隧道不可避免会受到地铁车站等基坑施工建设的影响[1-3]。

中外学者对基坑开挖引起邻近隧道结构变形进行了一系列的研究并取得了丰硕的研究成果。陈郁等[4]采用弹性地基梁理论简化模型，求解出的既有隧道位移变形值与实测数据相吻合。孙雅珍等[5]结合杭州某邻近地铁隧道工程,采用软件PLAXIS进行数值模拟分析，得出地表沉降、隧道位移等规律变化。张兵兵等[6]以济南历下医养结合中心项目近接地铁R3线施工为工程背景研究了基坑开挖对临近既有地铁隧道结构的影响，得到了隧道及基坑的变化峰值。姜峥[7]从理论方面出发对基坑开挖对临近管线的影响进行了分析。丁智等[8]系统性地从理论研究、模型试验、数值模拟和实测分析等方面分别阐述了软土基坑邻近施工问题的研究现状，对后续的研究有着很好的借鉴意义。李志高等[9]以实际工程背景，采用倒指数函数对基坑开挖过程中下覆盖隧道上浮值进行预测，将基坑的宽度和开挖时间效应提出为影响因素。基于成都5号线近接下穿既有3号线为工程，周庆国等[10]提出适应于成都砂卵石地层的预埋注浆加固保护方案。陈志伟等[11]结合流固耦合理论分析基坑开挖和降水对紧邻既有地铁隧道产生的影响，得出了基坑降水造成的地下水渗流的空间差异性。姜兆华等[12]运用室内模型试验以相对位置关系为影响因素，研究基坑开挖过程对邻近隧道的影响和隧道位移规律。李占峰[13]通过离心模型试验的方法，归纳总结了基坑卸荷阶段中地铁隧道的位移、管片应力、弯矩和围岩压力的变化规律；王海涛等[14]为研究隧道开挖对邻近管线变形的影响，以某区间隧道为工程为原型工程，开展了室内相似模型试验。

鉴于黄土独特的工程特性，在该地区进行的隧道工程与基坑工程相互作用机理较为复杂，基坑开挖过程中，其与隧道的相对位置关系、卸荷平面尺寸、开挖深度、既有地铁的地层条件等因素都对隧道结构位移产生影响，然而，目前却缺乏有效的分析能够完整地展示施工过程中黄土地层基坑开挖对地铁隧道的影响。因此，现基于西安地铁八号线幸福林带近接隧道工程为依托，采用正交试验组，分析基坑与隧道相对位置等影响因素下部隧道位移的影响程度，并进一步结合室内模型试验的方法，研究开挖卸荷导致既有隧道结构的变形规律，为后期基坑近接既有隧道的工程提供借鉴和参考。

1 影响因素敏感性分析

1.1 正交试验设计

正交试验设计以正交原理为基础，采用统计学的分析方法，从全面试验中挑选一些具备显著代表性的点开展多因素、多水平试验[15]，所选取的点具有“均匀分散、齐整可比”的特点[16-18]，因而通过正交试验可以找出各个因素的主次关系和最有组合，是一种化繁为简的高效率研究方法。

在研究过程中考虑到实际工程中的地质条件难以改变，故不分析既有隧道所处的地质条件对隧道变形的影响。基坑开挖过程中，开挖卸荷的深度、支护结构体系、时空效应及基坑与隧道的水平及竖直位置关系等是影响近接运营地铁结构安全的主要因素[19-21]。不同影响因素对隧道结构变形受力的影响程度不同。从隧道的空间位置关系角度出发，选取水平净距、竖直净距、嵌入深度和地连墙厚度四因素探讨黄土地层中土体卸荷对既有地铁隧道的影响，着重分析各影响因素下隧道管片的竖向和水平位移以及受力变化特征等，各个因素的具体形式如图1所示。

结合工程实际，最终确定4因素4水平正交试验，选用L16(44)正交表，共计需要做16组试验，所有的试验因素水平及试验方案如表1所示。

图1 影响因素Fig.1 Influencing factor

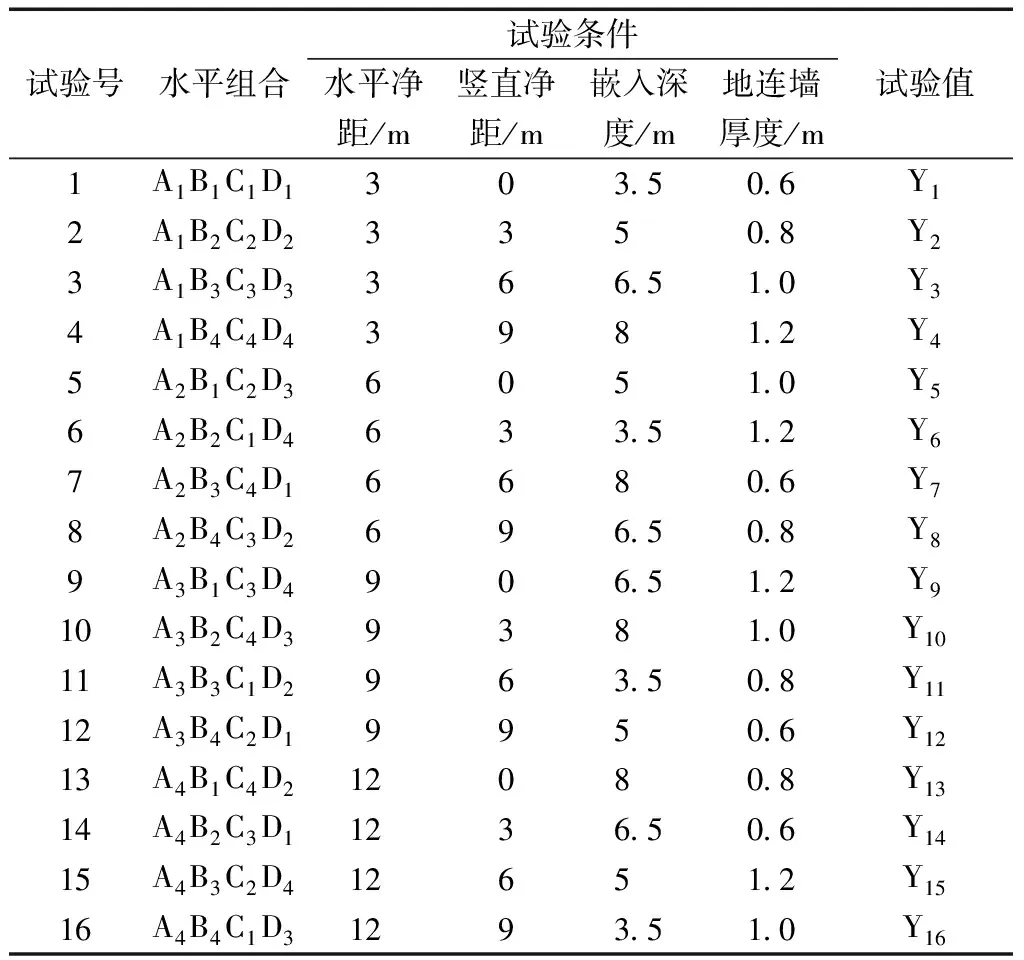
表1 正交试验因素水平及方案表Table 1 Orthogonal experiment scheme

1.2 正交数值模拟试验

1.2.1 数值模型与计算参数

根据圣维南原理，基于Midas GTS有限元软件，模型范围长×宽×深为150 m×110 m×50 m，工况1模型如图2所示，基于正交模型试验设计，通过改变相应影响因素参数大小共计建立类似16组模型。模型土体采用3D实体单元模拟，管片和基坑围护结构简化为2D板单元模拟，基坑内支撑均采用1D梁单元，整体模型施加自重和与约束。

模型土体采用修正摩尔库伦本构模型，相比于Mohr-Coulomb本构模型，模型参数能更接近实际情况，更能反映黄土的内在特性，土层参数如表2所示。基坑支护结构、隧道结构和加固结构性能参数参考相关规范和工程经验，如表3所示。基坑开挖前首先施作基坑围护结构，然后进行土体的开挖，开挖时竖向分层，每次开挖3 m，每步开挖完成后及时施作内支撑，直至开挖至基坑底部并浇筑底板。

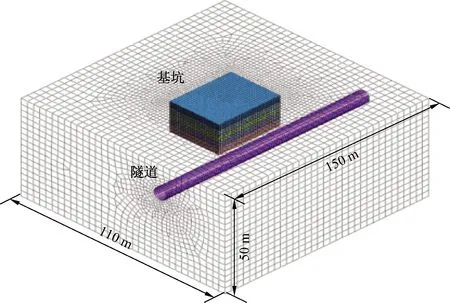
图2 工况1数值模型Fig.2 Numerical model of condition 1

表2 土层物理力学参数Table 2 Physical and mechanical parameters of soil layer

表3 结构材料力学参数Table 3 Mechanical parameters of structural materials

1.2.2 数值计算结果分析

表4为既有隧道最大竖向及水平位移值，可以看出，工况1时的最大竖向位移值较大，达到9.48 mm，工况15时的最大竖向位移值较小，仅有2.45 mm，四因素作用下竖向位移有着明显的差异性。而最大水平位移所受影响较小。各个工况最大水平位移变化范围处在0.86～2.27 mm，波动较小。

表4 既有地铁隧道正交试验最大竖向位移值Table 4 Maximum vertical displacement of existing metro tunnel in orthogonal test

1)隧道竖向位移方差分析

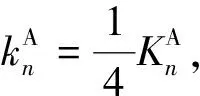
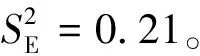
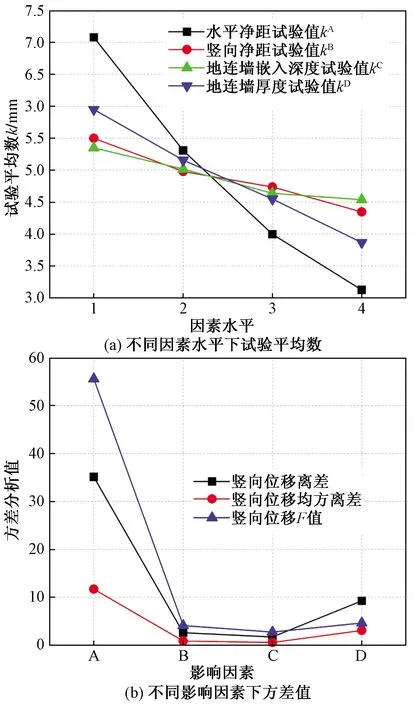
图3 既有隧道竖向位移方差分析Fig.3 Variance analysis of vertical displacement of existing tunnel

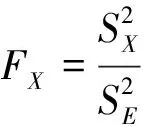
2)隧道水平位移方差分析

图4 既有隧道最大水平位移极差图Fig.4 Maximum horizontal displacement range of existing tunnel

由各因素的均方离差可知，各试验因子对隧道竖向位移的影响次序(从大到小)依次为：因子B(竖直净距)、因子D(地连墙厚度)、因子A(水平净距)、因子C(嵌入深度)。上述分析中，方差分析与极差分析的结果略有差异，在极差分析中，对隧道水平位移的影响D>B，两个因素极差试验值只差0.1。在方差分析中，则是B>D，方差试验值相差也较小且远大于F0.005(3，3)=47.47。综上，考虑试验结果的可信度，认为隧道与基坑的竖直净距对既有隧道结构水平位移的影响最大，地连墙的嵌入深度则对既有隧道结构的水平变形位移基本无影响。

2 基坑开挖近接隧道模型实验研究

通过正交试验组的分析，得知基坑与隧道的数值净距和水平净距分别对隧道的竖向位移和水平位移产生较大影响。在试验结果的基础上，基于室内模型试验，通过改变基坑与隧道的相对位置设置不同的工况，研究不同位置关系下隧道支护结构受力与变形的变化情况，分析基坑开挖对邻近隧道结构影响的基本规律。

2.1 室内试验方案设计

此次模型试验涉及的9个关键相似参数，包括几何尺寸l、容重γ、应力σ、应变ε、位移δ、弹性模量E、黏聚力c、内摩擦角φ和泊松比μ。根据试验条件和试验目的确定几何相似比Cl=1∶40，容重相似比Cγ=1∶40，根据量纲分析原理和方程可导出各物理量的相似比关系为：CE=CRc=CC=ClCγ=40。其他无量纲的物理量包括应变、泊松比、摩擦角的相似比均为1，即Cε=Cμ=Cφ=1。

图5 室内试验模型Fig.5 Indoor model test

2.2 试验模型属性

本试验模型箱如图5所示，模型尺寸设置为150 cm×150 cm×62 cm(长×高×宽)，基坑尺寸为60 cm×30 cm×25 cm(长×高×宽)。试验过程中土体采用相似材料填筑，确定石膏、膨润土、石英粉、石英砂的混合物作为围岩材料，其围岩材料[22]配合比为M粉∶M砂∶M土∶M膏∶M水=6∶7∶3∶3∶2，测得的材料参数试验结果如表5所示，基本满足试验相似比要求。

表5 模型试验土体力学参数[22]Table 5 Soil mechanical parameters of model test[22]

地铁隧道管片衬砌由钢筋混凝土制成，衬砌采用的是C50混凝土，内径540 cm，壁厚30 cm，其弹性模量约为34.5 GPa，泊松比为0.2。按照几何尺寸的相似常数为Cl=40，隧道模型内径为13.5 cm。根据三组测试结果选择最为合适的水膏比为1∶1.35，此时对应原弹模为33.8 GPa，进一步换算出模型衬砌厚度约为8 mm。模型围护结构采用聚乙烯板，弹性模量约为600 MPa，泊松比为0.2，长度为55 cm，高度为35 cm，厚度约为6 mm。聚乙烯板共计两块，设置在基坑的长边，入土深度为10 cm。

2.3 试验步骤及测量方案

2.3.1 测点布置

模型试验沿隧道纵向布置2个测量截面，分别距隧道中心截面各10 cm，在截面A处设置应变片及压力盒，在截面B处设置应变片及橡胶棒，以便测量隧道结构的横轴向变形、土压力变化及结构的竖向内径和水平向内径变化，如图6所示。

图6 管片测点布设图Fig.6 Layout of segment measuring points

2.3.2 工况设置及试验步骤图

通过改变两个主要影响因素：基坑与隧道结构之间的水平净距和竖直净距，分析基坑开挖过程对隧道结构影响的变化规律，鉴于此确定5组工况，如图7所示。具体流程如下：①调试器材；②分层填筑土层；③记录测试初始值；④基坑采用竖向分层的方式开挖，第1步开挖6 cm；第2步开挖12 cm；第3步开挖18 cm；第4步开挖至基坑底部，并记录测试数据；⑤重复步骤②～步骤⑤，进行下一组工况的实验测试，记录数据。

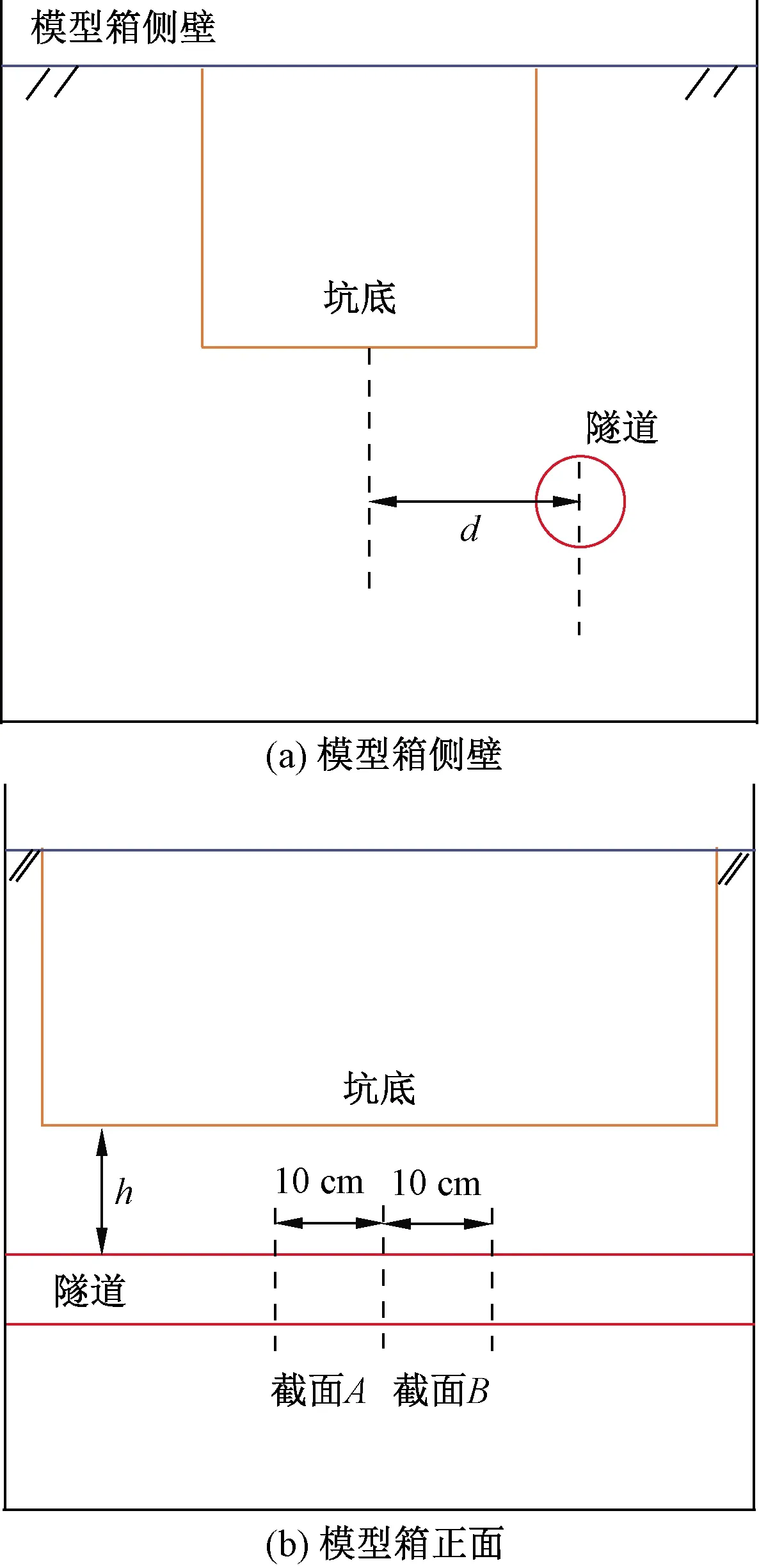
图7 试验工况Fig.7 Test conditions

2.4 试验结果分析

2.4.1 管片变形分析

图8为不同工况下管片的收敛位移变化规律，负值表示橡胶棒压缩，管片内径减小，正值表示橡胶棒拉伸，管片内径增加。由图8(a)可得，对于3个工况的竖向收敛位移，均经历了先增大后减小的过程，而水平收敛位移则经历了先减小后增大的过程，水平内径的变化规律则与竖直内径相反，并且整个开挖过程，管片的拉伸值均大于压缩值。工况1管片的竖向内径在第二步开挖时开始减小，第二步开挖完成后由拉伸变为压缩状态，此后不断被压缩。基坑开挖完成后，水平拉伸值为0.56 mm，竖向压缩值为0.43 mm。工况2管片的竖向内径在第三步开挖时开始减小，在第四步开挖阶段，由拉伸变为压缩状态，最终水平拉伸值为0.19 mm，竖向压缩值为0.12 mm。工况3管片的竖向内径在前三步一直增加，第四步开挖过程中开始减小，最终竖向拉伸值为0.38 mm，水平压缩值为0.29 mm。

由图8(b)可得，工况4管片的收敛位移变化规律与工况3基本一致，管片的竖向内径在前三步一直增加，第四步开挖过程中开始减小，最终竖向拉伸值为0.54 mm，水平压缩值为0.44 mm；工况5管片的竖向内径一直呈现压缩的状态，压缩值不断增大，水平伸长量不断增大，最终水平拉伸值为0.61 mm，竖向压缩值为0.54 mm。

对比5个工况，当水平净距保持一致，随着竖直净距的增加，管片逐渐从横向拉伸变形变为竖向拉伸变形，且竖直净距越大，每一开挖步对应竖向内径收敛值越大，水平内径收敛值越小。当竖向净距保持一致，随着水平净距的增加，管片横向拉伸的趋势越来越明显，且水平净距越大，竖向内径收敛值越小，水平内径收敛值越大。这是由于水平净距一定时，起到变形主导因素的是卸荷引起的竖向附加应力，竖直净距越大，竖向附加应力对管片作用越明显，管片竖向拉伸变形越明显。竖向净距一定时，水平净距越大，水平向附加应力的作用越明显，管片横向拉伸变形越明显。

隧道的收敛位移变化规律主要是由于基坑与既有隧道的水平净距较小，当基坑开挖深度较浅，围护结构可以抵挡基坑外侧的土体发生水平向位移，但基坑内土体的移除会引起坑底土体的隆起，这个阶段的土体主要体现为竖向变形，对于隧道而言，土体变形引起的隧道竖向变形更显著，出现竖向拉伸值增大，水平向压缩值增大的规律。随着开挖深度的增加，围护结构逐渐向坑内变形，导致土体的水平位移不断增大，隧道水平向受拉应力影响更显著，从而导致水平向拉伸的趋势越来越明显。

2.4.2 管片弯矩分析

管片两个截面的弯矩变化规律基本一致，选取截面A试验数据进行分析。管片的弯矩变化规律如图9所示。从图9(a)可以看出，3个工况管片弯矩变化规律一致，随着基坑的开挖，拱顶和右墙弯矩值不断增大，拱底和左墙弯矩值先减小后增大。3个工况拱顶弯矩值分别增加了11.13%、7.7%、4.04%；拱底弯矩值分别增加了0.84%、-1.53%、-4.08%；左墙弯矩值分别增加了1.51%、-1.63%、-5.39%；右墙弯矩值分别增加了9.61%、7.08%、4.0%。对比3个工况，随着竖直净距的增大，对应的管片弯矩也越大，管片弯矩值增量越来越小。

从图9(b)可以看出，3个工况管片弯矩变化规律基本相同。3个工况拱顶弯矩值分别增加了4.19%、7.7%、9.24%；拱底弯矩值分别增加了-6.03%、-1.53%、1.45%；左墙弯矩值分别增加了-6.0%、-1.63%、1.97%；右墙弯矩值分别增加了4.0%、7.08%、8.5%。对比三个工况，水平净距越大，管片弯矩越大，管片弯矩的增量越大。

2.4.3 管片周围土压力分析

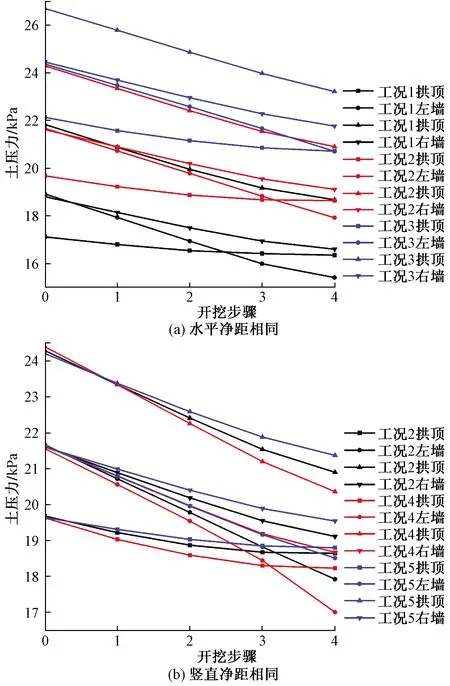
图10 对比分析水平净距及竖直净距相同时不同 工况下土压力变化Fig.10 The variation of earth pressure under different working conditions with the same horizontal clearance and vertical clearance

管片周围土压力变化规律如图10所示，由图10(a)可知，3个工况管片的周围土压力变化规律一致，随着开挖的进行，管片周围土压力逐渐减小，且竖向受到向下的土压力差不断减小，水平受到指向基坑的土压力差不断增大，从而引起隧道朝上和基坑方向移动。管片周围土压力整体呈现拱底土压力值>拱顶土压力值，右墙土压力值>左墙土压力值的规律。对比三个工况的周围土压力值，工况3>工况2>工况1，说明隧道埋深越大，管片周围土压力值越大，与管片弯矩的变化规律一致。基坑开挖完成后，3个工况拱顶土压力值分别减小了6.41%、5.26%、4.52%；拱底土压力值分别减小了14.46%、13.98%、13.04%；左墙土压力值分别减小了18.52%、17.28%、15.02%；右墙土压力值分别减小了11.69%、11.57%、11.00%，随着竖直净距的增加，管片周围土压力变化越来越小，说明卸荷对管片周围土压力影响减小，且基坑开挖对管片左墙位置处的土压力变化影响最大。

从图10(b)可以看出，三个工况周围土压力变化规律相同，且与图9(b)所示的工况规律一致。开挖过程中，对比三个工况的周围土压力值，工况5>工况2>工况4，说明水平净距越大，管片周围土压力值越大，与管片弯矩的变化规律相同。基坑开挖完成后，3个工况拱顶土压力值分别减小了6.41%、5.26%、4.31%；拱底土压力值分别减小了16.58%、13.98%、11.71%；左墙土压力值分别减小了21.13%、17.28%、14.41%；右墙土压力值分别减小了13.75%、11.57%、9.54%，基坑与既有隧道的水平净距越大，管片周围土压力变化越小。通过对比5个工况，得出隧道与基坑的相对位置越近，卸荷对隧道周围土体应力的影响越明显。

3 结论

利用正交试验和室内模型试验的研究方法，分析了基坑与隧道相对位置和基坑围护结构的影响性以及开挖过程中隧道管片收敛、弯矩和周围土压力的变化规律，得出如下结论。

(1)以既有隧道最大竖向位移值作为检验评价标准时，基坑距既有隧道的水平净距对既有地铁稳定性影响最大；以既有隧道最大水平位移值作为评价标准时，基坑底距既有隧道的竖直净距对既有地铁隧道稳定性的影响最大。

(2)基坑开挖的过程中，管片的拉伸变化始终大于压缩变化。当水平净距相同，随着竖直净距的增加，管片水平内径由拉伸变为压缩，管片竖向内径由压缩变为拉伸；当竖向净距相同，随着水平净距的增加，管片横向拉伸和竖向压缩的趋势越来越明显。

(3)管片弯矩值分布在-21～21 kN·m。基坑与隧道竖直和水平净距越大，管片弯矩越大，同时随着竖直净距的增大，管片弯矩的变化减小；随着水平净距的增大，管片弯矩的变化增大。

(4)管片周围土压力在卸荷过程中保持着一直减小的变化规律。隧道周围的土压力呈现拱底土压力>拱顶土压力，右墙土压力>左墙土压力的规律。竖直净距和水平净距越大，管片周围土压力值越大。