复杂接触下大理岩球砾碰撞破碎特征

柳镕林， 曾亚武， 叶阳， 孙翰卿， 刘洋

(武汉大学土木建筑工程学院， 武汉 430000)

落石是山区地区常见的自然灾害之一，具有突发性高、随机性强特点，极大影响山区人民生命财产安全[1-2]。对于落石灾害，防治核心工作之一是研究块石的运动轨迹，而块石沿边坡运动过程中破碎现象时常发生，块石破碎会影响块石的运动轨迹，进而影响防护结构的设计[3-4]。为准确预测块石的运动轨迹，需要深入开展块石碰撞破碎特征研究，而在复杂接触条件下进行块石撞击模拟则是准确研究撞击破碎特征的关键。

在冲击试验方面，中外学者利用大理石系统开展了岩石块体碰撞试验[5-7]，详细研究冲击角度、冲击速度、冲击力等[8-13]主要因素对块石损伤破碎的影响。大量有关落石冲击角度的研究表明，落石大多发生在坡度角50°～90°的斜坡处，而且斜坡坡度越大，越有利于形成危岩的形成[8-9]。在实际工程中落石的撞击速度通常大于7 m/s，小于25 m/s[9-12]，杨少军等[13]建议试验时将落石冲击最大速度规定为25 m/s左右。冲击力方面，许泽鹏等[14]展开室外中低速落石冲击试验研究，揭示出落石最大冲击力与速度之间符合幂函数关系。在试样破碎度分析方面，Deniz[15]的研究介绍了t10指标，即量筛筛析通过初始平均粒径十分之一的碎片百分比，在粉碎、化工和矿物工程中被广泛用于评价颗粒的破碎程度。Narayanan等[16]提出t10指标与冲击能量的关联方程，以此分析特定条件下试样冲击时的粉碎能量。

在对块石进行冲击试验探究裂纹扩展及破坏过程时，分离式霍普金森杆(split Hopkinson pressure bar，SHPB)加载试验系统被广泛使用[17-19]。范翔宇等[20]利用SHPB系统研究加载速率等因素对页岩裂纹扩展演化的影响；陈俊宇等[21]通过SHPB系统对砂岩进行动态冲击压缩试验，并观察试样在微观条件下的破坏模式。

综上所述，针对块石撞击模拟分析破碎特征的研究已经积累了一定成果，但相关研究主要局限于某种特定接触模式下落石撞击的冲击模拟，并不能全面地分析块石冲击时的各种复杂接触模式，而且选取SHPB系统进行相关研究虽有涉及，但仍显欠缺，值得开展进一步的研究和探讨。

为此，现针对如冲击角度、接触面粗糙度、冲击速度等主要影响因素，依托SHPB系统进行创新型改进，并对大理石球砾进行撞击模拟实验，详细分析相关因素对试样破碎时临界速度、破碎特征以及尺寸分布的影响，进一步探究并分析大理石球砾撞击破碎特征，以期为落石灾害防治提供思路。

1 试验与研究方法

1.1 试样及垫块制备

制备了一批直径为40 mm的大理岩岩球和13种不同角度、粗糙度的钢质垫块来开展球砾碰撞破碎试验。所有大理岩岩球均由湖南耒阳采石场中一块约1.5 m3的大理岩岩块加工而成，以保证岩球力学性能的一致性。制备岩球试样前，首先将大理岩岩块切割成边长约为50 mm的立方体。随后，利用圆柱形磨床将立方体加工成直径40 mm的大理岩岩球。最后，通过抛光机对大理岩球进行抛光处理，以提高球体的加工精度。岩球加工完成后，为了减小缺陷(如节理)对实验结果的影响，筛除了含有节理的大理岩球[22]。

图1 试验所用大理岩球Fig.1 The marblespheres used in the experimental tests

其中大理石球的球度φ[22]计算公式为

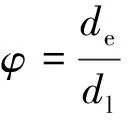
(1)

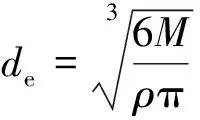
(2)

式中：de为岩球的等效直径；dl在球体三维方向中最长的直径；M为球体质量；ρ为球体密度。使用精度为±0.01 g的电子秤和精度为±0.02 mm的游标卡尺测量球体质量为(90.69±4.9) g，直径为(40.12±0.56) mm。因此，试验所制备的岩球平均球度为0.983，精度较高，可以满足试验要求。试验中垫块为Cr12MoV钢材。钢垫块与大理岩球砾的基本力学性能参数如表1所示。垫块的强度远高于大理岩球砾，因此撞击时接触区不会发生塑性变形或碎裂[5]。

试验时，通过设置不同类型的垫块来改变大理石球砾冲击时的冲击角度和接触面粗糙度。冲击角度θ为入射速度矢量与上半碰撞面之间的夹角[23]，均布尖齿角度为α，如图2所示。所有垫块表面均布尖齿，垫块的冲击角度θ及均布尖齿角度α如表2所示，其中10号垫块均布尖齿高度为2 mm，其余所有垫块均布尖齿高度均为1 mm。

表1 大理岩球砾和垫块钢基本性能力学参数[5]

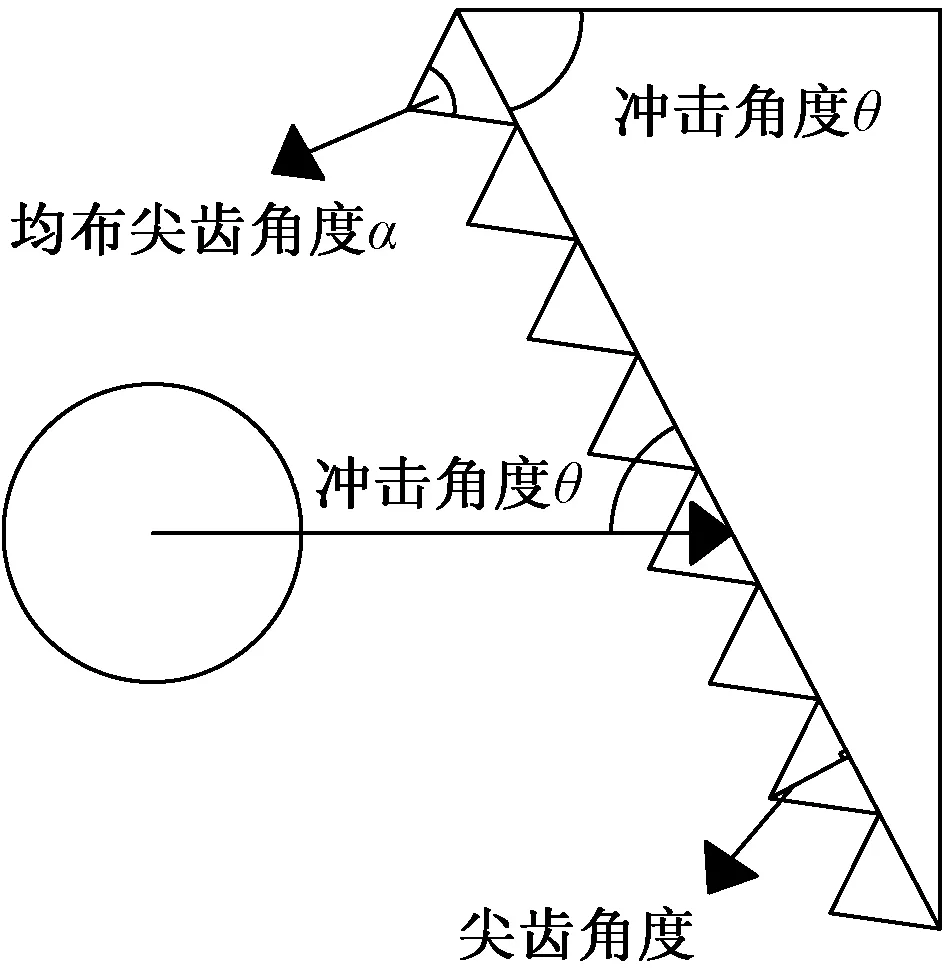
图2 冲击角度θ及均布尖齿角度α示意图Fig.2 Illustration of the impact angle θ and the serration tooth angle α

表2 各垫块冲击角度及均布尖齿角度表

1.2 试验设备

冲击试验在武汉大学岩土与结构工程安全湖北省重点实验室的分离式霍普金森杆加载试验系统(SHPB)上进行。压杆直径为50 mm，入射杆长为2 500 mm，动弹性模量为250 GPa，密度为7 784 kg/m3，弹性波速度为5 667.2 m/s。试验时，发射腔内部放入圆杯形钢套筒，钢套筒内径50.34 mm，外径62.38 mm，长度为176.92 mm。钢套筒外部涂抹碳粉，并压实置于发射腔中。试验过程种，钢套筒携带试样撞击在入射杆上。图3为试验装置示意图。试验时，在垫块与入射杆撞击面相接处适度涂抹抗磨锂基脂薄层，并用垫块环固定，放置摄影灯以及高速摄影机于距设备500～700 mm处，设置每秒传输帧数为17 500～22 500 帧[24]后进行试验。

图3 改进SHPB试验装置示意图[25]Fig.3 The advanced diagrammaticFigure of the SHPB test device[25]

2 试验结果分析

试验结束后，利用PFA软件分析高速摄影机拍摄图样，分析试样的速度以及撞击破碎模式。根据Narayanan等[16]的研究，试样破碎后通过平均尺寸的1/n的试样碎片累积分数与t10指标有关，确定试样破碎后t10指标可以确定试样破碎后的碎片的尺寸分布，而且t10指标与试样冲击时的粉碎能量有关，因此将试样碎样通过4 mm量筛进行筛分，来评估试样的破碎程度。而分析撞击破碎图样可知，随速度增加，试样撞击时变形逐渐累积[26]，会经历4种典型裂纹发育阶段，如图4所示。

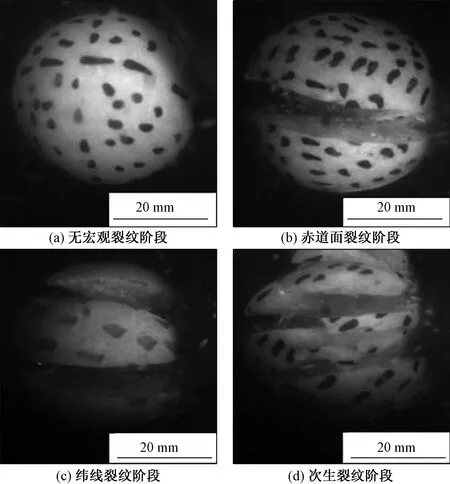
图4 4种试样撞击典型破碎阶段Fig.4 Four typical impact failure stages of specimens

如图4所示，第1阶段为无宏观裂纹阶段(non-macroscopic cracks)，试样在撞击后产生弹性形变回弹，并无宏观纵贯裂纹；第2阶段为赤道面裂纹阶段(equatorial plane cracks)，试样撞击产生弹塑性变形，在试样赤道面接触变形边界处产生拉伸应力并引发纵贯裂纹[27]，试样开始破坏；第3阶段为纬线裂纹阶段(parallel cracks)，碰撞速度的增加导致了撞击时接触圆直径的增加和锥状区域的扩大，弹塑性变形延伸到接触面产生的环拉应力发育出与赤道面平行的纬线裂纹并形成破碎细锥[27]；第4阶段为次生裂纹阶段(secondary cracks)，此时试样在撞击侧失去了圆锥形或半椭球形的形状，形成不平行于纬线裂纹，且大多垂直于纬线裂纹的次生裂纹，并沿着撞击的方向传播[27-28]，此时试样裂纹充分发育，较高的冲击速度使细锥膨胀，从而使试样的剩余部分减小。

2.1 冲击角度θ=90°、尖齿角度α=180°时球砾碰撞试验结果

2.1.1 临界速度及破坏模式

表3所示为当冲击角θ=90°，尖齿角α=180°时，试样在各冲击破坏典型阶段间临界速度及冲击力。试样冲击速度为5.76 m/s，冲击力达到31.86 kN时出现纵贯裂纹，发生弹塑性形变进而破坏；而后冲击力每增加10～15 kN则转换破坏模式。

图5为当冲击角度θ=90°、尖齿角度α=180°时，垫块传递的最大冲击力F随冲击速度v的变化曲线，由图5可知，F相对v呈幂函数正相关增大趋势，其关系大体上接近于幂函数[14]，且随着速度增大，冲击力F相比速度的变化率逐渐降低。由图5可知，曲线在速度为9 m/s处前后有较大的斜率差异，结合表3可知，原因在于此时试样裂纹变化分别处于从赤道面裂纹阶段到纬线裂纹阶段的过程中，试样破碎模式发生变化，试样内部空隙和破碎细锥数量增多，锥状区域的扩张，垫块对于最大冲击力的传递能力也因此而发生变化。

表3 θ=90°、α=180°时试样在各冲击破坏典型阶段 所需临界速度及冲击力(齿高1 mm)Table 3 The required velocityand impact force of the sample at each impact failure typical stage node when θ=90° & α=180° (The tooth height is 1 mm)

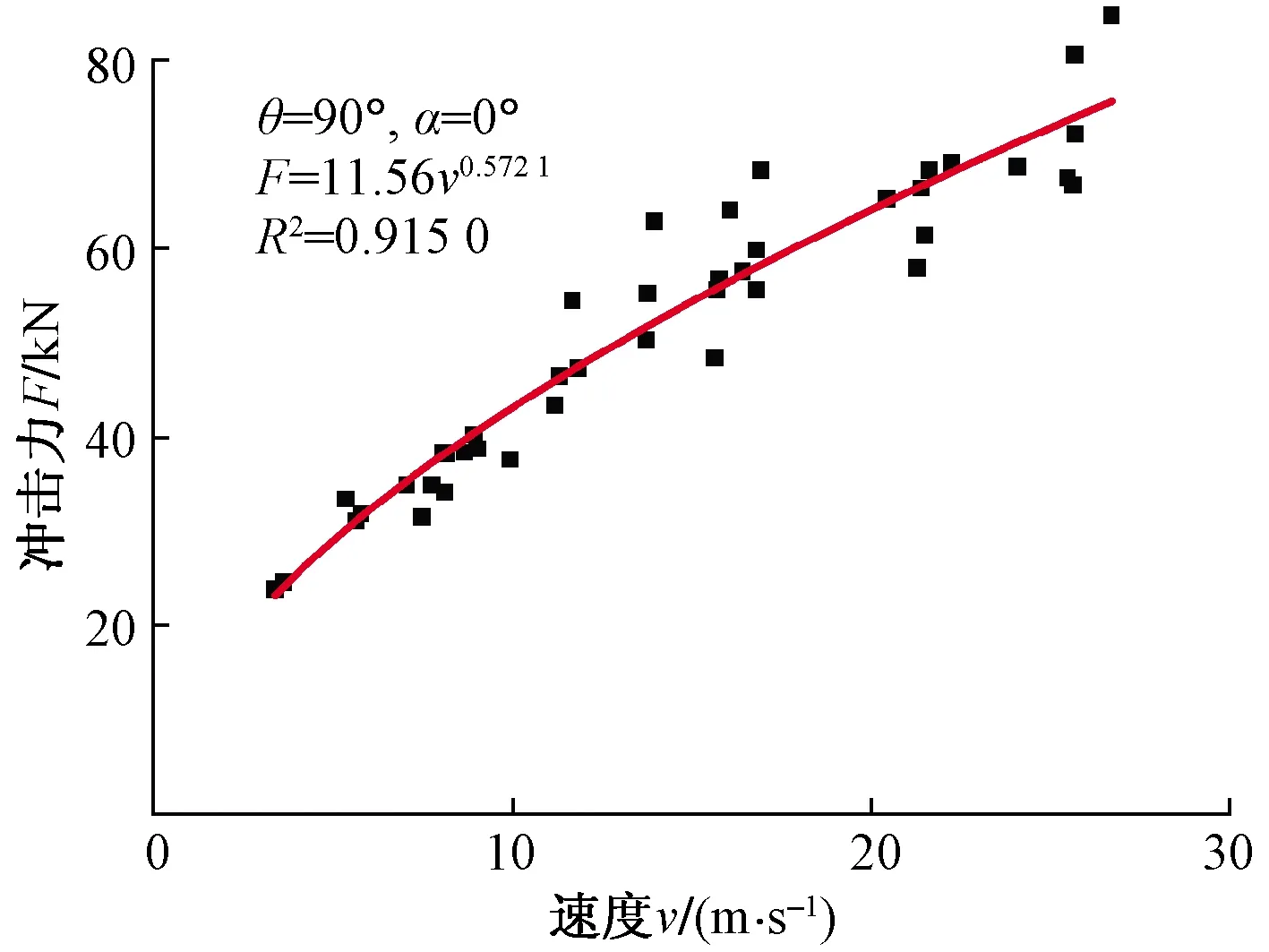
图5 θ=90°, α=180°时最大冲击力-速度变化曲线图Fig.5 The maximum-impact-force-velocity behavior when θ=90° & α=180°

2.1.2 碎片筛析结果

图6为冲击角度θ=90°、尖齿角度α=180°时，试样冲击后进行4 mm粒径筛析得出的t10指标数值随冲击速度变化的曲线。

图6 θ=90°，α=180°时t10指标数值-速度变化曲线图Fig.6 The t10-value-velocity behavior when θ=90°& α=180°

由图6可知，θ=90°、α=180°时t10数值区间为[0，0.18]，t10指标数值随着速度增加而逐渐增大。当试样处于无宏观裂纹阶段时试样破坏率较小，t10数值接近0；而处于赤道面裂纹和纬线裂纹阶段时试样开始逐步破坏，由于环向拉力导致锥状区域的扩张和破坏率增加，t10数值接近0.055；次生裂纹阶段试样开始发展出次生裂纹，结构不稳定性增加，冲击时进一步破坏，裂纹随机发育，破坏率达到最大，t10数值达到0.18，裂纹扩展随机，试样大部均破裂为8 mm左右的碎屑。

2.2 冲击角度θ变化、尖齿角度α=180°时球砾碰撞试验结果

2.2.1 临界速度及破坏模式

当冲击角度θ分别为80°、60°、45°，尖齿角度α=180°时，按照不同冲击角度进行冲击试样在各冲击破坏典型阶段间的临界速度如表4所示。

表4 冲击角θ变化、尖齿角度α=180°时试样在 各冲击破坏典型阶段所需临界速度(齿高均为1 mm)Table 4 The required velocity of the sample at each impact failure typical stage node when θ changes & α=180° (The tooth height is 1 mm)

由表4可知，冲击角度θ越大，试样在各冲击破坏典型阶段所需临界速度越小，即速度一定时，试样越容易破裂发育裂纹并进入下一个破坏阶段，但趋势不明显。而速度一定时，试样在撞击时冲击力的法向分量随着冲击角度θ的减小而减小，而结合Ye等[29]的研究，此时冲击力的法向分量主导破碎，因此冲击角度越小，试样越不易破碎发育裂纹。而由图7分析试样破坏图样可知，冲击力切向分量使得试样部分区域产生剪应力和压应力，并在特定区域内延伸弹塑性变形，而法向分量较小时，相比正碰作用试样较难发育出整体性赤道面裂纹等纵贯裂纹[1]，反而出现上半部分破碎，下半部分较完整的情况。

图7 冲击角度45°≤θ<90°时试样破坏特征示意图Fig.7 The failure characteristics of specimens when 45°≤θ<90°

而且冲击角度θ分别为80°、60°、45°时，试样在从无宏观裂纹阶段进入赤道面裂纹阶段所需速度分别为冲击角度θ=90°时所需速度的1.661倍、1.665倍、1.681倍，这说明冲击角度45°≤θ<90°时试样从无宏观裂纹阶段发育出第一条赤道面纵贯裂纹进而破坏相比θ=90°具有较大的阻碍作用，而且分析表3及表4可知阻碍作用随着冲击角度θ的减小而增大，冲击角度θ一定时随着速度的增加而减小。

2.2.2 碎片筛析结果

图8为冲击角度θ分别为80°、60°、45°，尖齿角度α=180°时，试样冲击后进行4 mm粒径筛析得出的t10指标数值随冲击速度变化的曲线，各垫块的t10随着速度增加而逐渐增大。由图8可知保持α=180°不变，θ=80°时t10区间为[0，0.157]；θ=60°时t10区间为[0，0.134]；θ=45°时t10区间为[0，0.107]，相比于θ=90°时破坏率均有所减小，说明45°≤θ≤90°时试样最终的破坏率随着冲击角度θ的减小而降低。

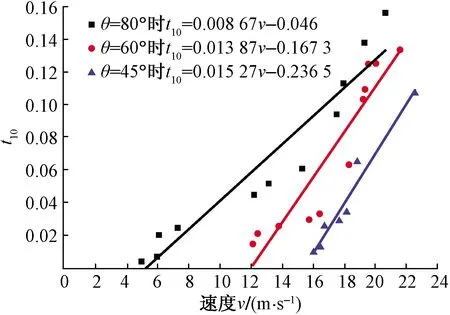
图8 冲击角度θ变化，尖齿角度α=180°时 t10-速度变化曲线图Fig.8 The t10-velocity behavior when θ changes & α=180°

由图8可知，冲击角度越大则t10相对速度的变化率越小，但一定速度下冲击角度越大，试样的破坏率越大，试样越容易破碎，与上文分析结论一致。

2.3 冲击角度θ=90°、尖齿角度α变化时球砾碰撞试验结果

2.3.1 临界速度及破坏模式

表5为冲击角度θ=90°，尖齿角度60°≤α≤120°时，试样在各冲击破坏典型阶段所需临界速度及冲击力。结合表3可知，尖齿高度固定，尖齿角度60°≤α≤120°时，尖齿角度α越小，试样在各冲击破坏典型阶段所需临界速度越小，即速度一定时，试样越容易破裂发育裂纹并进入下一个破坏阶段，但趋势不明显。尖齿角度α一定时，尖齿高度越小，试样在各冲击破坏典型阶段所需临界速度越小，即速度一定时，试样越容易破裂发育裂纹或进入下一个破坏阶段。

齿高不变时，而且尖齿角度α分别为60°、90°、120°时，试样在从无宏观裂纹阶段进入赤道面裂纹阶段所需速度分别为尖齿角度α=180°时所需速度的2.162倍、2.183倍、2.237倍，这说明尖齿角度60°≤α≤120°时试样从无宏观裂纹阶段发育出第一条赤道面纵贯裂纹进而破坏相比α=180°具有较大的阻碍作用，而且综合分析表5及表3可知阻碍作用随着尖齿角度α的增大而增大，尖齿角度α一定时随着速度的增加而减小。

由图9分析试样破坏图样可知，尖齿角度60°≤α≤120°时试样撞击到垫块时内部存在可以引发裂纹的环拉应力，但是接触面的尖齿增大表面摩擦，进而产生环箍效应，限制接触面破碎细锥膨胀扩张和裂纹发育，增强了试样的冲击刚度[30]，因此α=180°试样冲击破碎时纬线裂纹互相平行，且与接触平面垂直，而在60°≤α=≤120°试样冲击时纬线裂纹呈相交于接触面的趋势。

表5 冲击角θ=90°，尖齿角度α变化时在各冲击破坏典型阶段所需临界速度及冲击力Table 5 The required velocity & impact force of the sample at each impact failure typical stage node when θ=90° & α changes

图9 尖齿角度α=180°及60°≤α≤120°时试样 破坏特征对比图Fig.9 The comparison diagram of specimen failure characteristics when α=180° and 60°≤α≤120°

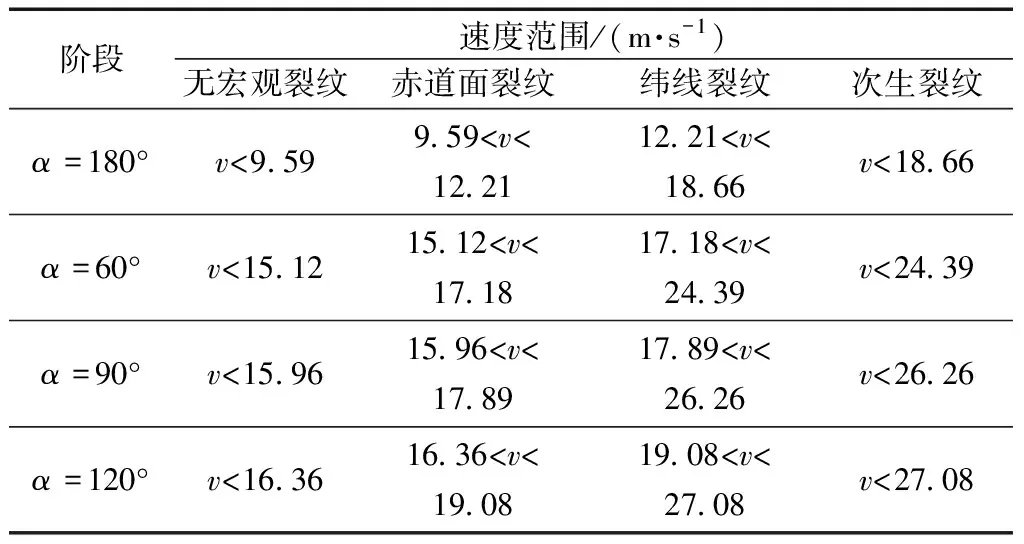
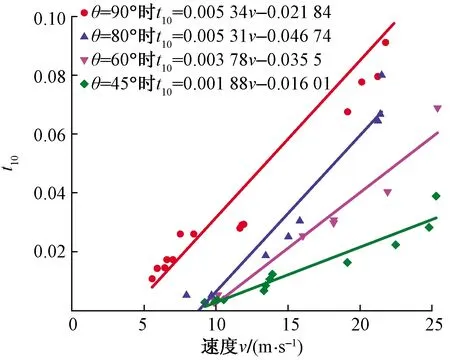
另外结合表5及表3可知，冲击角度θ=90°、尖齿角α变化、齿高为1 mm时，试样在各冲击破坏典型阶段所需的临界冲击力F满足Fα=180°

图10 θ=90°、齿高为1 mm、α变时垫块最大 冲击力-速度变化曲线图Fig.10 The maximum-impact-force-velocity behavior when θ=90°, tooth height=1 mm & α changes

图10为当冲击角度θ=90°，齿高为1 mm，尖齿角度α分别为60°、90°和120°时，垫块传递的最大冲击力F随冲击速度v的变化曲线，F与v呈幂函数正相关增大趋势，其关系大体上接近于幂函数[14]。由图10可知，垫块尖齿齿高不变时，试样能传递到垫块的冲击力相对于速度的变化率随尖齿角度增大而减小，而且速度一定时，θ=90°，60°≤α≤120°时，α越大则垫块传递的冲击力越小。另外由图10可知当齿高为1 mm，冲击速度v在7 m/s左右时，试样裂纹发育处于无宏观裂纹阶段，尖齿角度α=90°与α=120°时垫块对于冲击力的传递能力相似，冲击力均约为25 kN；当齿高为1 mm，冲击速度v在15m/s左右，试样裂纹发育处于赤道面裂纹及纬线裂纹阶段转换过程时，尖齿角度α=90°与α=60°时垫块对于冲击力的传递能力相似，冲击力均约为58 kN。

图11为当冲击角度θ=90°，尖齿角度α=90°，齿高变化时，垫块传递的最大冲击力F随冲击速度v的变化曲线，F与v呈幂函数正相关增大趋势，其关系大体上接近于幂函数[14]。由图11可知，当冲击角度和尖齿角度不变，试样能传递到垫块的冲击力相对于速度的变化率随尖齿高度增大而减小。而且速度一定、θ=90°、60°≤α≤120°时，尖齿高度越大则垫块传递的冲击力越小。

图11 θ=90°、α=90°、齿高变化时垫块最大 冲击力-速度变化曲线图Fig.11 The maximum-impact-force-velocity behavior when θ=90°, α=90° & the tooth height changes

2.3.2 碎片筛析结果

图12为冲击角度θ=90°、尖齿角度α变化时、试样冲击后进行4 mm粒径筛析得出的t10随冲击速度变化的曲线，各垫块的t10随着速度增加而逐渐增大。由图可知保持θ=90°不变，α=60°时t10区间为[0，0.14]；α=90°，齿高为1 mm时t10区间为[0，0.136]；α=90°时，齿高为2 mm时t10区间为[0，0.056]，α=120°时，t10区间为[0，0.08]，相比于α=180°时破坏率均有所减小，说明60°≤α≤120°时试样最终的破坏率随着尖齿角度α的增加而降低，随着尖齿高度的增加而降低。

图12 冲击角度θ=90°、尖齿角度α变化时 t10-速度变化曲线图Fig.12 The t10-velocity behavior when θ=90° & α changes

另外由图12可知，接触面尖齿齿高不变时，t10数值相对速度变化率绝对值随尖齿角度增大而减小；而当尖齿角度不变，t10相对速度变化率绝对值随尖齿高度增大而减小。由2.3.1节可知，当试样冲击速度为15 m/s左右时，尖齿角度α=90°与α=60°时垫块对于冲击力的传递能力相似，结合图12可知，此时t10,α=90°

2.4 冲击角度和尖齿角度的影响

2.4.1 临界速度及破坏模式

表6和表7为冲击角θ变化、尖齿角度α变化时，试样在各冲击破坏典型阶段所需临界速度。结合表3～表5可知，当尖齿高度一致，速度一定时，冲击角度θ与尖齿角度α对试样发育裂纹或进入下一个破坏阶段的影响趋势，与2.2节和2.3节结论一致，但相比2.2节及2.3节变化趋势较为明显。

由表6和表7可知，试样开始破坏发育赤道面裂纹时所需速度排序为vθ=90°,α=180°

表6 冲击角度θ=60°，尖齿角度α变化时各冲击破坏 典型阶段间临界速度(齿高均为1 mm)

表7 尖齿角度α=60°、冲击角度θ变化时各冲击 破坏典型阶段间临界速度(齿高均为1 mm)Table 7 The required velocity of the sample at each impact failure typical stage node when α=60° & θ changes (The tooth height is 1 mm)

2.4.2 碎片筛析结果

图13为冲击角度θ=60°，尖齿角度α变化时，试样冲击后进行4 mm粒径筛析得出的t10随冲击速度变化的曲线，各垫块的t10随着速度增加而逐渐增大。

图13 冲击角度θ=60°、尖齿角度α变化时t10- 速度变化曲线图Fig.13 The t10-velocity behavior when θ=60° & α changes

由图13可知，θ=60°、α=180°时t10区间为[0，0.134]；θ=60°、α=60°时t10区间为[0，0.069]；θ=60°、α=90°时t10区间为[0，0.055]；θ=60°、α=120°时t10区间为[0，0.038]，当尖齿高度一致，速度一定时，尖齿角度α对试样最终破坏率的影响与2.3节结论一致。另外当接触面尖齿齿高和冲击角度θ不变时，t10相对速度变化率绝对值随尖齿角度α的增大而越小，与2.3节结论一致。

图14 尖齿角度α=60°，冲击角度θ变化时 t10-速度变化曲线图Fig.14 The t10-velocity behavior when α=60° & θ changes

图14为尖齿角度α=60°、冲击角度θ变化时，试样冲击后进行4 mm粒径筛析得出的t10随冲击速度变化的曲线，各垫块的t10随着速度增加而逐渐增大。由图14可知，θ=90°、α=60°时t10区间为[0，0.14]；θ=80°、α=60°时t10区间为[0，0.08]；θ=60°、α=60°时t10区间为[0，0.069]；θ=45°、α=60°时t10区间为[0，0.039]，当尖齿高度一致，速度一定时，冲击角度θ对试样最终破坏率的影响与2.2节结论一致。

3 结论

采用改进的SHPB系统开展了大理岩球碰撞试验，研究了冲击角度、接触面粗糙度、冲击速度等主要影响因素对试样破碎时临界速度、冲击力、破碎特征等方面的影响，得出如下结论。

(1)当冲击角度θ=90°，尖齿角度α=180°时，试样冲击速度为5.763 m/s，冲击力达到31.86 kN时出现纵贯裂纹，发生弹塑性形变进而破坏；而后冲击力每增加10～15 kN则改变破坏模式。

(2)冲击角度45°≤θ≤90°，尖齿角度α=180°，速度一定时，冲击角度θ越大则试样越容易破裂发育裂纹或进入下一个破坏阶段，试样的破坏率随着冲击角度的增大而增大，试样越容易破碎；冲击角度45°≤θ<90°时试样从无宏观裂纹阶段发育出第一条赤道面纵贯裂纹进而破坏相比θ=90°具有较大的阻碍作用，且阻碍作用随着冲击角度θ的减小而增大，随着速度的增加而减小。

(3)冲击角度θ=90°，尖齿角度60°≤α≤120°，速度一定时，尖齿高度一定时，尖齿角度α越小，试样越容易破坏，裂纹发育更完全，试样最终的破坏率随着尖齿角度α的增加而降低。尖齿角度α一定时，尖齿高度越小，试样越容易破裂发育裂纹或进入下一个破坏阶段，试样最终的破坏率随着尖齿高度的增加而降低。尖齿高度一致时，尖齿角度60°≤α≤120°时试样从无宏观裂纹阶段发育出第一条赤道面纵贯裂纹进而破坏相比α=180°具有较大的阻碍作用，且阻碍作用随着尖齿角度α的增大而增大，随着速度的增加而减小。

(4)相同的冲击力作用下，尖齿角度α=180°时最容易破坏，尖齿角度α=120°和尖齿角度α=60°次之，尖齿角度α=90°时最不容易破坏。而当冲击角度θ=90°，尖齿角度α=90°，齿高变化时，相同的冲击力作用下，尖齿高度越高试样越容易破坏。速度一定时，θ=90°，60°≤α≤120°时，尖齿角度越大则垫块传递的冲击力越小，尖齿高度越大则垫块传递的冲击力越小。

(5)改变尖齿角度60°≤α≤120°相比改变冲击角度45°≤θ<90°更能阻碍试样发育赤道面裂纹进而破坏。