基于分布式光纤温度监测的气井产出剖面解释——以中国南海永乐区多层合采探井为例

吴木旺， 郑永建， 隆腾屹， 段永刚， 魏明强

(1.中海石油(中国)有限公司湛江分公司， 湛江 524057； 2.西南石油大学石油与天然气工程学院， 成都 610500)

随着油气资源开发领域的进一步拓展和开发技术的进步，实时反馈井下地层生产情况已经成为高效开发此类气藏的重要突破点，特别是具有高温高压带有井下复杂情况的多层合采气井井下生产剖面状态实时反馈需求更为迫切[1-4]。

图1 分布式光纤测温原理图Fig.1 Schematic diagram of DTS temperature measurement

目前各大油田常用的产出剖面监测仪有多参数测井仪[5]、流体扫描成像仪[6-7]以及阵列式成像测井仪[8]等，但这些监测技术存在着一些缺陷：成本高、监测距离受到限制、需要有特定监测井以及专门的探测井；面对复杂井下情况容易失效，施工工艺要求较高；信息滞后，解释结果不准确等。而中外光纤技术飞速发展，分布式光纤温度传感监测(distributed temperature sensing，DTS)的精度有了很大的提高，且DTS下入工艺简单，能适应复杂井下地质情况，探测范围广泛[9]。DTS技术能清晰地了解这类气井井下动态生产的温度和压力，通过对温度、压力分析解释可落实井下生产状态，对合理调整井下工作制度和提高井工作效率和经济效益具有重要意义[10]。近年来，中外学者关于DTS解释理论方面进行了相关探索研究。Ramey[11]、Wilhite[12]、Sagar等[13]提出热传导、导热系数的计算方法；Hasan等[14]、Kabir等[15]、Sui等[16]提出不同相态的传热规律。Dada等[17]提出温度变化对储层参数影响。文献[18-19]将应力敏感和体积压裂(stimulated reservoir volume，SRV)改造体积考虑在内，提出二者对油井产出剖面温度的影响。文献[20-21]基于SA、MCMC算法建立反演模型，验证裂缝半长与井筒温度剖面的关系。然而目前鲜见对多层合采非稳态气井方面的产出剖面解释研究。为此，现从低渗气藏渗流规律出发结合渗流过程发生的能量损耗、热传导、对流传热等微热因素的影响建立低渗多层合采气井产出温度剖面特征预测模型，并结合现场实际测试数据开展产出剖面应用研究，以期为DTS监测技术在多层合采气井中应用提供理论基础。

1 DTS技术原理

DTS技术是将光纤投入井下，井口发射激光，光在传播过程中产生拉曼反射(包含斯托克峰和反斯托克峰)，通过计算斯托克峰和反斯托克两部分强度比值，由此以获得精确的温度[22]，测温过程如图1所示。随着技术进步、精度提升，在油田中也出现了DTS技术的应用：如气举监测、流动剖面解释和稠油热采监测等。在油田实际应用中常规光纤安装位置为套管外壁[23]、油管外壁[24]和油管内部[25]：套管外壁和油管外壁属于永置式安装，不可回收，利于对作业施工全周期温度剖面监测；油管内部属于可回收式安装，适用于短周期温度剖面监测。

2 模型建立

现有温度解释理论多围绕直井稳态来展开的，且温度模型未将热传导、对流传热等 一些微量的热效应全部考虑在内。目前针对DTS监测多层合采气井的产出剖面解释研究鲜见报道，为此笔者建立考虑多微量热效应的多层合采气井温度剖面预测模型。模型假设条件如下：①气层为多层，各个储层的厚度、孔隙度和渗透率均不等；②储层为均质储层，每一层气体流动为单相气；③原始地层压力为Pi，原始地层温度为Ti，日产气量为qi；④流体的高压物性与压力和温度相关，且流动假设符合达西定律同时考虑焦耳汤姆逊、热辐射等诸多微热效应；⑤储层之间无窜流现象出现，气体满足径向流特征，同时不受重力的影响。

根据假设条件，首先根据质量守恒及运动方程建模，给出压力场非稳态渗流模型(双介质),连续性方程为

(1)

内边界条件为

(2)

外边界条件为

(3)

式中：p为地层压力，MPa；r为到井中心距离，m；t为生产时间，d；φ为孔隙度，%；k为渗透率，mD；ct为综合体弹性压缩系数，MPa-1；μ为黏度，mPa·s；h为储层厚度，m；q为流量，m3/d；rw为井半径，m；re为供给边界，m。

温度场渗流模型，考虑热传导、热对流等微热反应，通过能量方程将这些反应联系起来建成连续性方程为

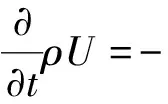
(4)

(5)

式中：t为时间，s；ρ为流体密度，kg/m3；p为压力，MPa；τ为黏滞耗散系数，W/(m·℃)；U为单位质量能量，J/kg；v为速度，m/s；t为温度，℃；H为单位质量焓，J/kg。

2.2 模型求解

将压力场方程及边界条件离散求解，编写网格并构建系数矩阵求解如下形式：

(6)

式(6)中：上标n、n+1为n、n+1时刻；下标i-1、i和i+1为i-1、i和i+1网格位置；pwf为井底流压，MPa；pe为边界压力，MPa；d和λ为常数。

将温度场渗流模型离散后与压力场耦合求解，可得

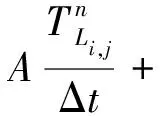
(7)

式(7)中：T为温度， ℃；下标Li为储层第Li小层；下标j-1、j和j+1为j-1、j和j+1网格位置；Δt为时间步长，d；Δx为网格步长，m。

(8)

(9)

(10)

(11)

(12)

(13)

(14)

式中:b1为坐标转换系数；kL为某一气层的渗透率，mD；KLT为某一层的导热系数，W/(m·℃);TL为某一层温度，℃；βL为某一层的热膨胀系数；cpL为流体比热，J/(kg·℃)；ρL为某一层流体密度，kg/m3。

结合上述压力场非稳态渗流模型、温度场渗流模型以及压力场温度场耦合后的模型，编程求解。求解后模拟产量、生产时间和渗透率对温度剖面的影响。

根据上述模型，将储层分为三层，设置储层相关参数(表1)，可计算获得气体产出温度剖面。

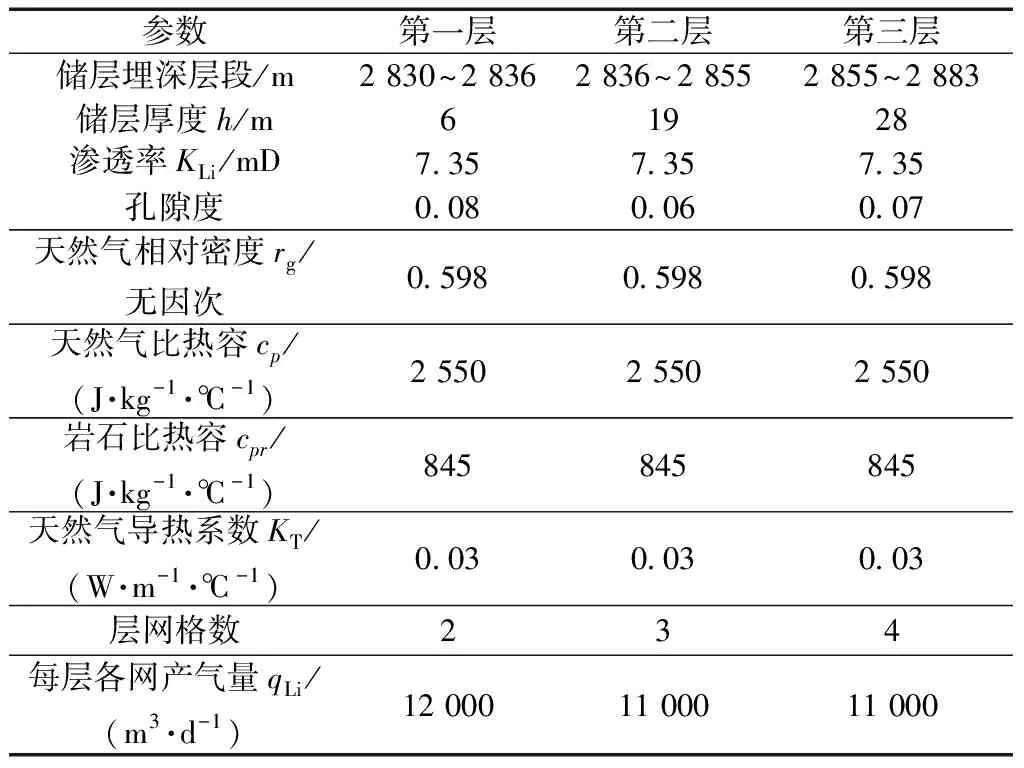
表1 计算相关基础参数表Table 1 Calculation of relevant basic parameters

图2(a)是根据上述假设，经过编程计算后模拟几个测试产量对温度的变化，Q1是每层各网格产气量，4条曲线是在Q1的基础上加减测试产量对温度的影响。从图2(a)可以看出产量对产出温度影响几乎是线性的；同一深度随着产量的增加温度减少，同时减少的幅度几乎是相等的；不同产量下，温度随深度变化导数几乎一致。

图2(b)是测试时间t对温度的影响，从图2(b)中可以看出，同一深度下随着生产时间的增加温度的增加，但是增加幅度是逐渐减少的；在生产时间大幅增加的情况下温度曲线趋势是接近重合的，由此判断在生产过程中，生产前期生产时间对温度有一定的影响，但是后期影响温度变化的主控因素不是生产时间。

图2(c)是不同渗透率下温度随深度的变化曲线。为了更加直观地观察渗透率对温度的影响，假设三个层段的渗透率相同。从图2(c)中可以看出，渗透率对产出温度影响十分显著，随着渗透率的降低产出温度增加大且增加的幅度逐渐增大，影响是非线性的；同时可以观察到，渗透率较低时，井底温度变化随着井深变化不明显，逐渐趋于平滑的直线。

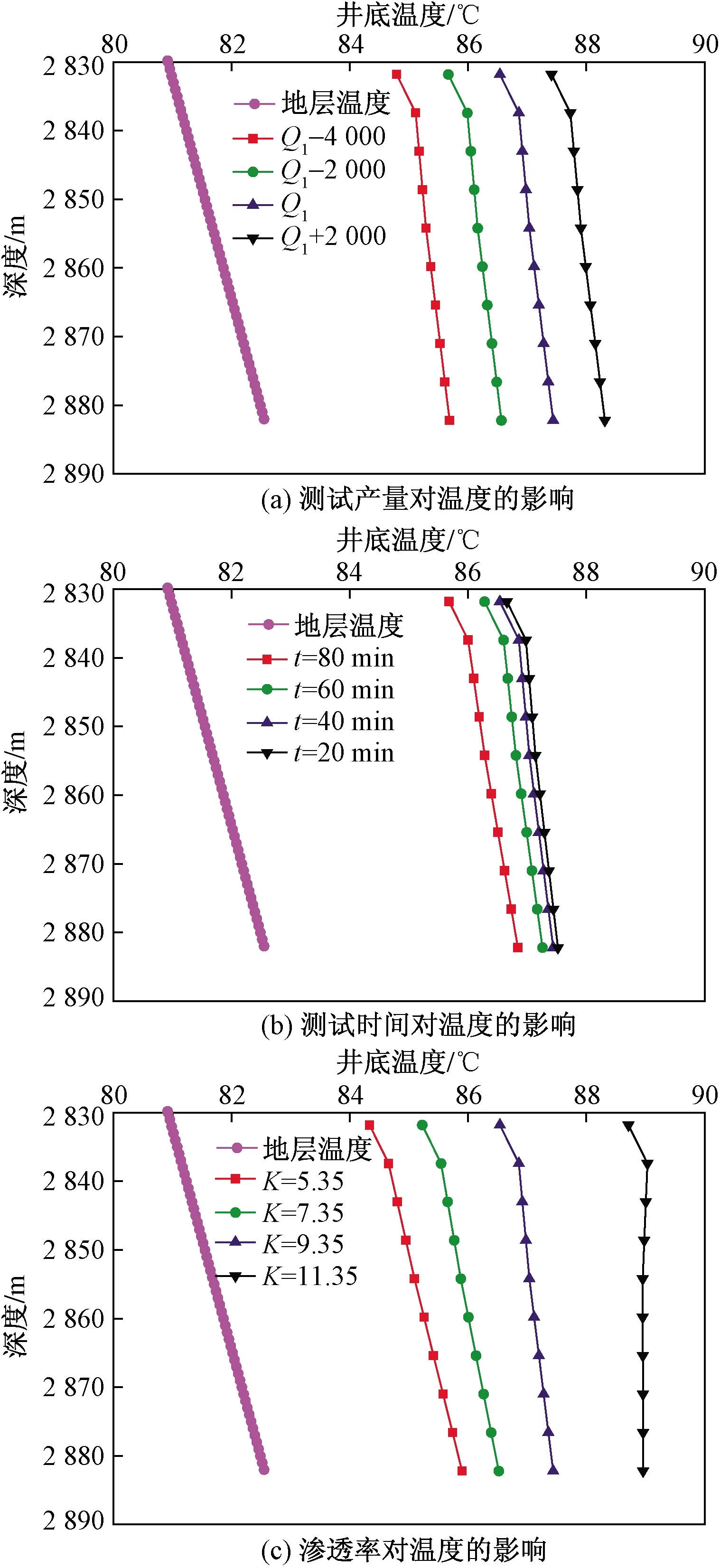
图2 不同因素对温度的影响Fig.2 Effects of different factors on temperature

3 现场实例

在机理模型计算的温度剖面结果及敏感性参数对其影响的分析基础上，结合用一口已知DTS测试曲线的实测井进行验证。

3.1 地质特征

Y井构造位于琼东南盆地松南低凸起部位，是一口探测井。该地区探测井大多出现小层或者大层段测试作业：储层呈现小层多，纵向非均质性强的特征。测试井段层位以崖城组砂砾岩和潜山风化壳为主。其中崖城组砂砾岩整体为中-高孔、中高渗-特高渗储层，测井解释以气层为主；潜山风化壳整体为中孔、中渗储层，测井解释以气层为主。测试井段测井解释结果物性参数如表2所示。

3.2 测试概况

Y井测试井井身结构如图3所示，管柱分隔器下部至133/8″，管鞋为27/8″油管，管鞋至引鞋为27/8″打油孔管。完井方式为裸眼完井，测试裸眼井段为2 793.7～2 936.0 m，测试层层位为前古近系。结合井身结构、完井方式和井下工况限制，将光纤下落到下图中2 900 m处。

在测试过程中，探井实施两开一关的施工措施，初开主要目的为清井取样；初关井是为储层压力恢复；二开井是为温度剖面解释提供测试依据，施工及测试概况如表3所示。

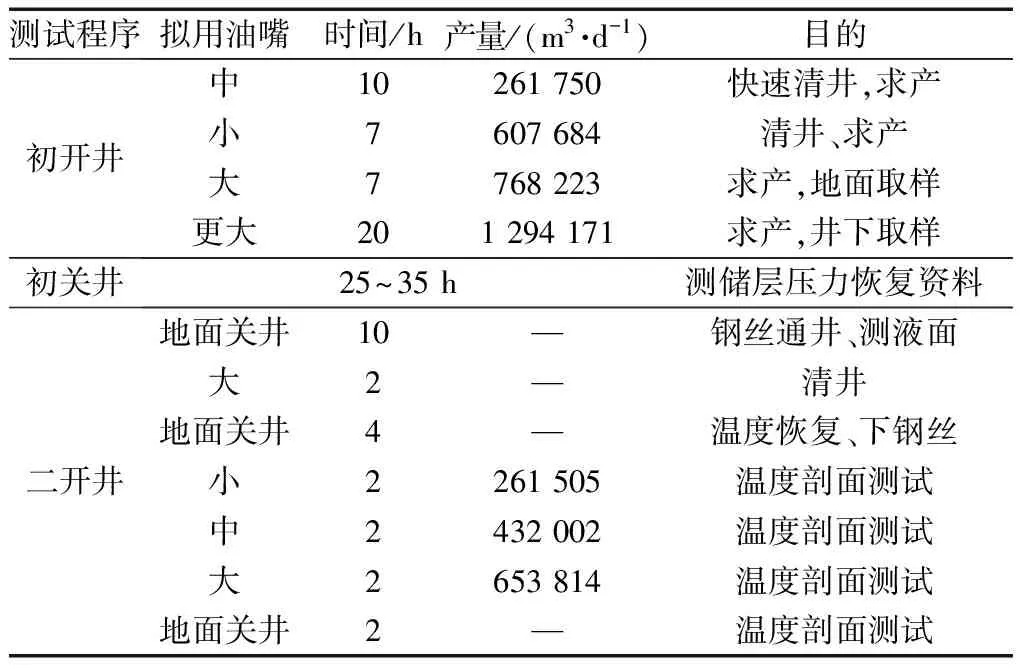
表3 施工概况Table 3 Construction survey

3.3 数据拟合及解释结果分析

在对DTS测试曲线拟合时发现：DTS数据波动较大，噪声明显，给数据的准确拟合带来较大的难度，会造成同一制度下的数据分析结果误差较大(图4)。以图4测试制度二DTS曲线为例采用全局概率法进行数据比较分析，进一步通过平滑滤波对数据进行预处理，获得了不同时刻正常趋势的数据，如图5所示。

进一步结合测井解释结果资料和测试温度随深度变化曲线特征，可将测试层段分为3段。其中第一段为2 828.8～2 886.31 m、第二段为2 886.31～2 896.26 m、第三段为2 896.26～2 900 m。

在上述测试数据处理基础上，利用建立多层合采气井温度剖面预测模型对该井三种测试制度下的三个DTS数据进行拟合比较分析(图6)，表4为实测试数据，表5是反演不同产层的贡献率。

图6(a)的结果表明，2 896.25～2 900 m产气贡献率为43.65%，2 900 m以下窜流约1.27×104m3/d。

图4 测试制度二DTS曲线Fig.4 DTS curve of test system 2

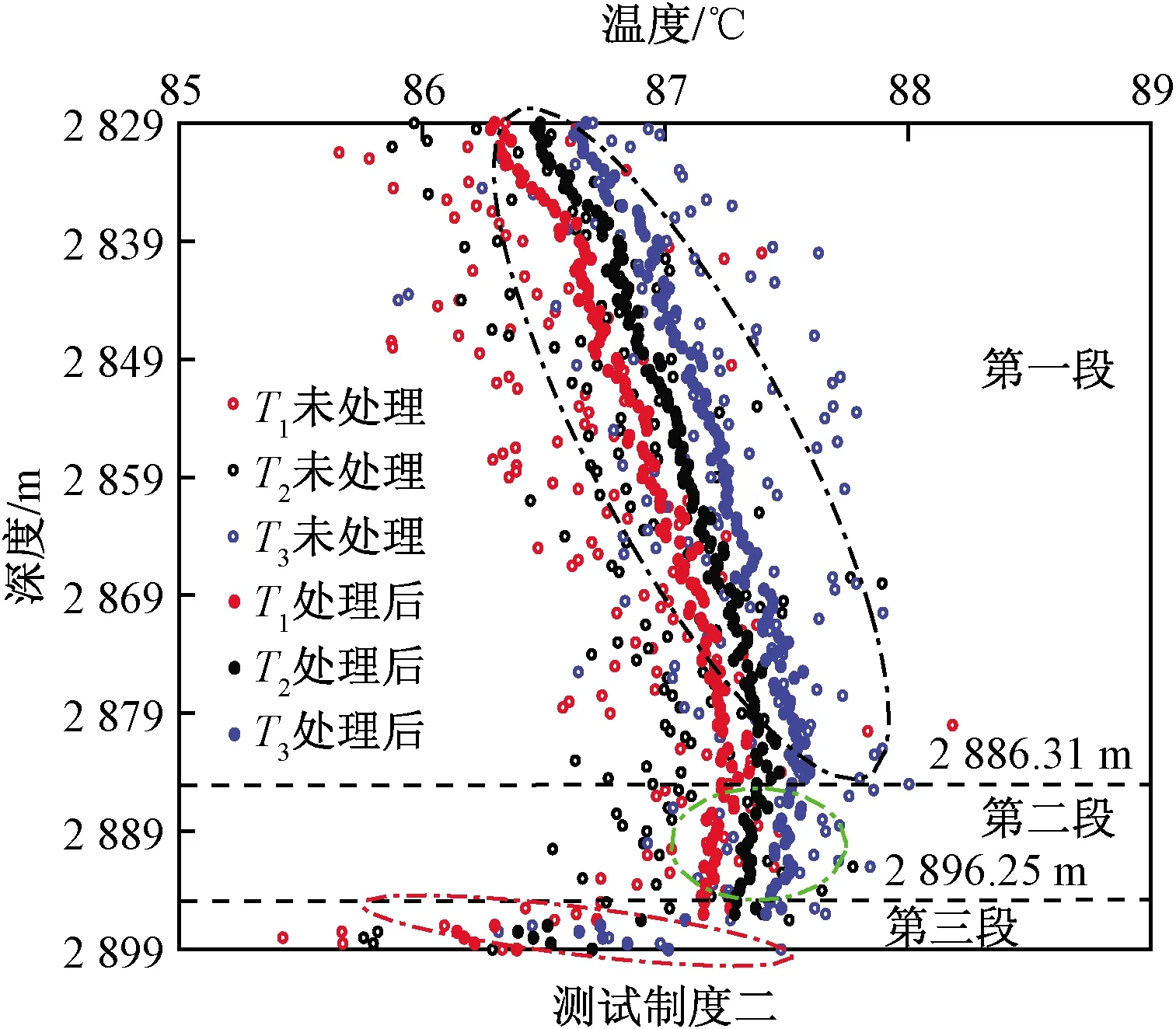
图5 全局概率法数据处理结果Fig.5 Data processing results of global probability method

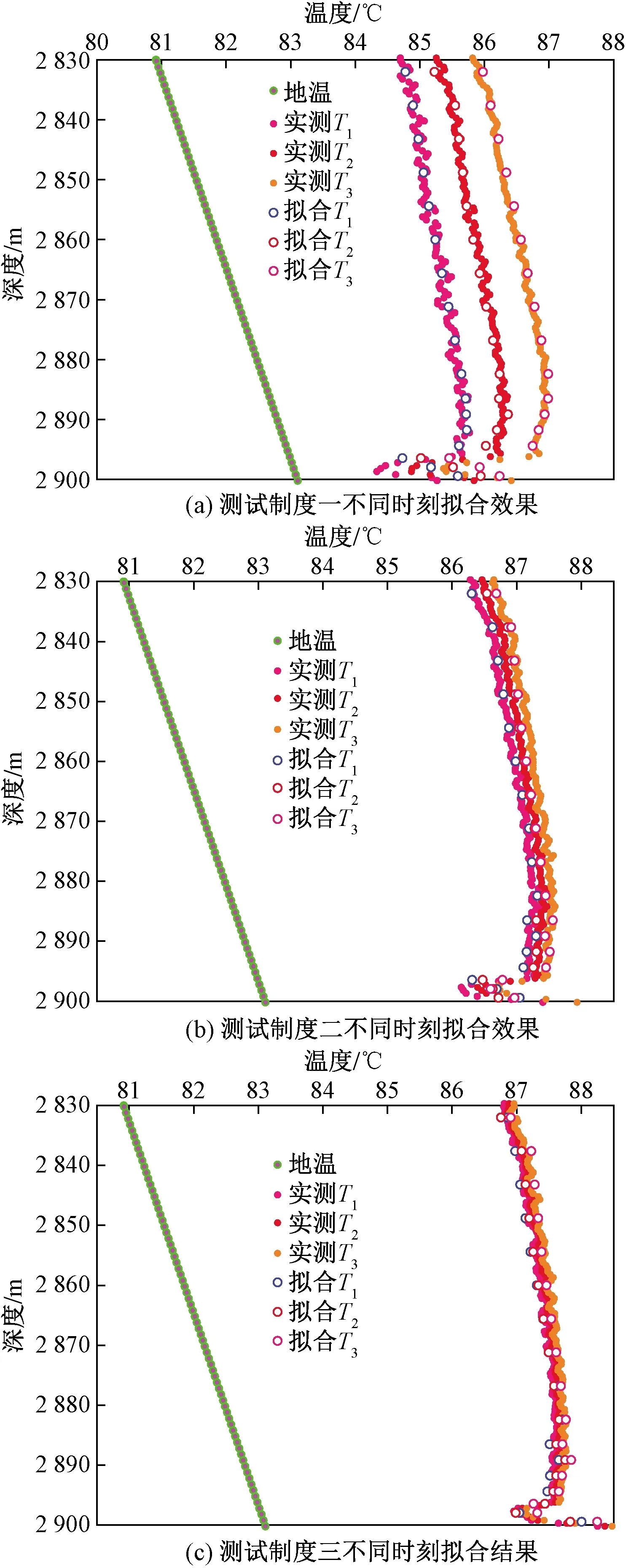
图6 三种制度下DTS数据拟合结果Fig.6 DTS data fitting results under three systems

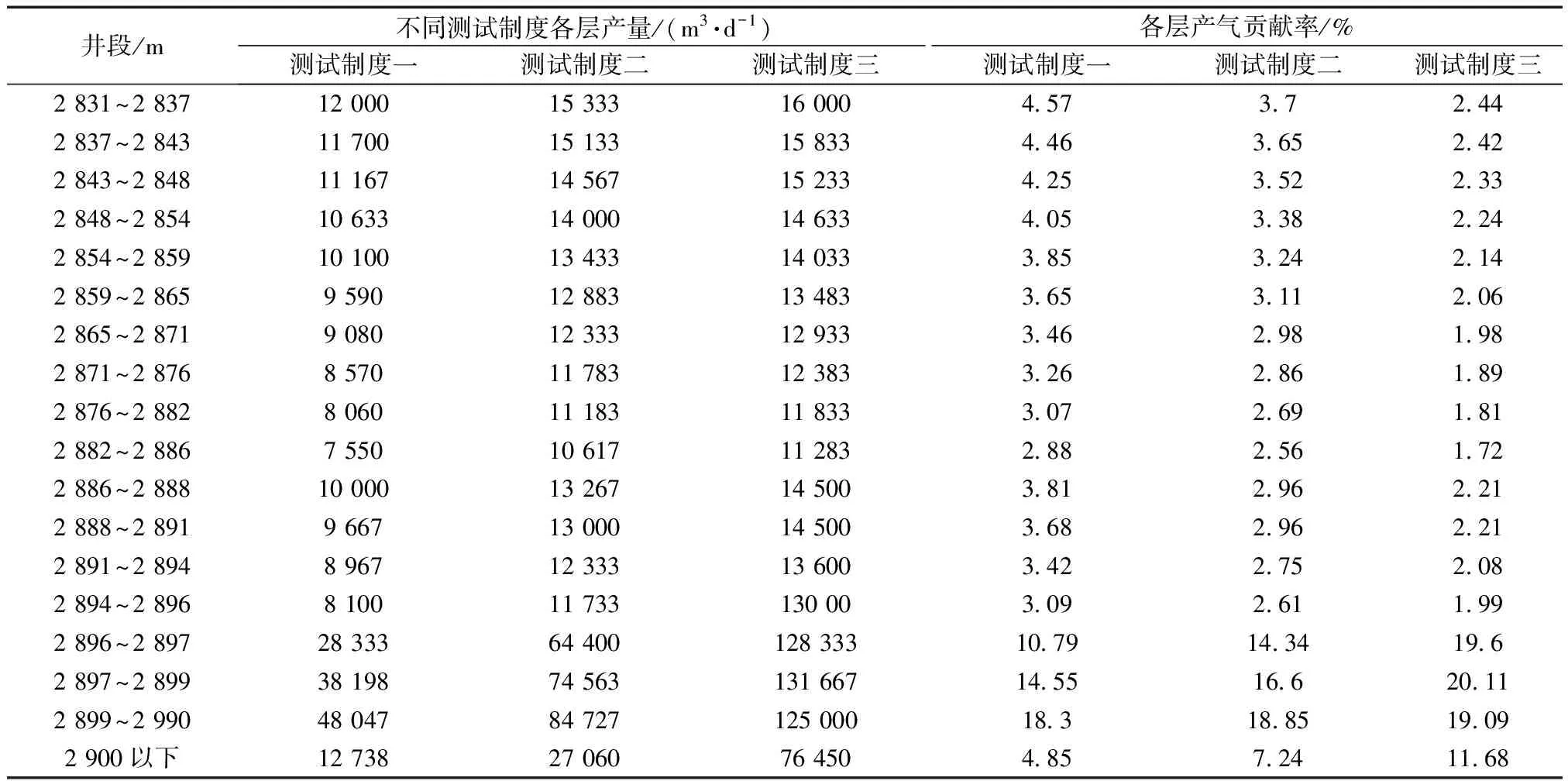
表4 三种制度下实际测试产量Table 4 Actual test output under three systems

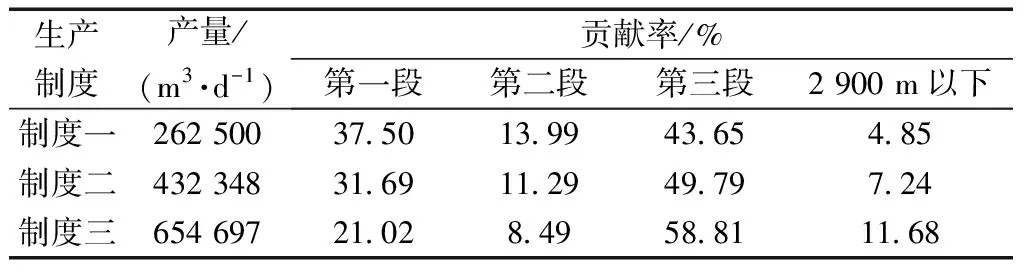
表5 反演不同生产制度下产层贡献率Table 5 Inversion of production layer contribution rate under different production systems

图6(b)的结果表明，2 896.25～2 900 m产气贡献率49.79%，2 900 m以下窜流约2.71×104m3/d。2 900 m，相比测试制度一，测试压差增大，下部主力层产量增加幅度大，且贡献率增加。

图6(c)的结果表明，2 896.25～2 900 m产气贡献率58.81%，下部气窜起量与7.645×103m3/d。相比测试制度一和制度二，下部主力产层产量增加幅度大，且贡献率增加。

结合三个测试制度下的测试结果和DTS反演的拟合结果，研究发现随着测试产量的增加，各层产量贡献均有所增加，但是第一段和第二段产层贡献率出现大幅下降，第三段的贡献率却大幅提升；增加产量的主力层仍然是下部2 896.25～2 900 m，并且2 896.25～2 900 m段温度出现显著降低，是高渗透带，为主要贡献层特征。这与实际生产测试结果解释一致也说明渗透率对高产储层影响更为明显。

4 结论

(1)根据能量守恒，热力学定律以及焦耳汤姆逊热效应等建立低渗气藏产出渗流压力-温度场耦合理论模型。

(2)计算揭示了多层合采气井产出剖面温度响应特征，计算结果表明：产量、生产时间和渗透率均对温度的变化有影响；渗透率变化，温度对其敏感程度变化最为明显，波动幅度最大，随着渗透率减少，产出剖面的温度增加，增加的幅度是非线性的。

(3)反演出Y井的产出剖面，随着测试产量的增加，各层产量均有不同幅度的增加，第三段主力层的产量增加幅度最大，对第三段的物性参数进行剖析，较于第一段和第二段的孔隙度、渗透率均有大幅度超越分，这与剖面温度响应特征对应，渗透率是主要其影响温度变化的主控因素。反演出各个层段的产量贡献也与实际生产测试解释结果一致，且产量主力层也与实际情况吻合。