电动汽车锂离子电池荷电状态估算方法综述

李军， 李虎林

(重庆交通大学机电与车辆工程学院， 重庆 400074)

当今，发展清洁能源汽车是缓和能源危机和环境危机的重要措施[1]。电动汽车(electric vehicles, EVs)是目前使用清洁能源的主要交通工具，动力电池组内的化学反应提供汽车工作所需的清洁的电能，在使用过程中具有零排放零污染等优点，但动力电池的技术当前极大地限制了EVs的发展。动力电池荷电状态(state of charge, SOC)估算可为其健康状态(state of health, SOH)、能量状态(state of energy, SOE)、功率状态(state of power, SOP)和寿命状态(state of life, SOL)等提供估计和计算基础，是一项重要的应用研究。准确的SOC估算可以从根本上将EVs动力电池过充过放情况发生的概率降到最低，从而提升动力电池的工作性能和使用寿命，增加EVs续航能力。

1 锂离子电池结构及工作原理

动力电池的相关技术指标(如能量密度、功率密度、经济性、低温-高温性能、寿命等)会直接影响EVs的续航能力、安全性、舒适性、使用年限等用户现实的情况需要。相对来说，锂离子电池(lithium-ion battery, LIB)兼备能量密度高、功率密度高、循环寿命长、环境友好等优点，具有优秀的综合性能，是当前较为理想的EVs动力电池。但目前传统的采用液态电解质的LIB现已逐渐无法满足发展需要[2]，而新型的全固态锂电池(solid-state lithium-metal-battery, SLMB)技术还不成熟无法替代传统LIB，下文讨论以传统LIB为主。

1.1 锂离子电池的基本结构

具有优秀综合性能的LIB广泛应用于航空航天、医疗、通信等领域的电子电器设备中，其基本结构如图1所示。

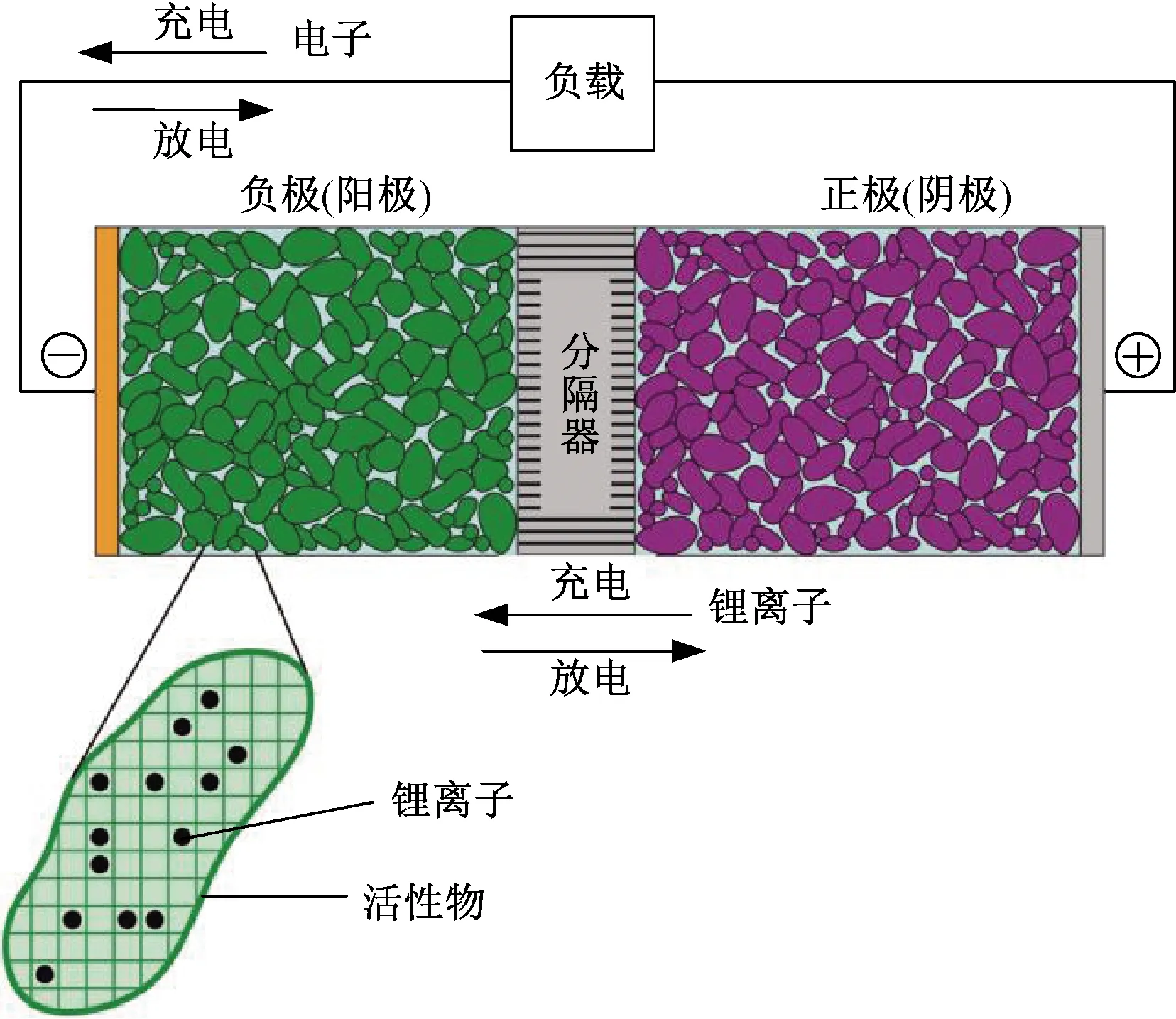
图1 LIB基本结构图[3]Fig.1 The structures of the LIB[3]

图1清晰地显示了LIB的最基本结构：LIB内的主要物质是活性物(用于储存Li)、分隔器和各类添加剂黏合剂组成的液态电解质。正负极储Li粒子由分隔器隔开避免直接接触，若正负极储Li粒子直接接触会发生剧烈的化学反应，短时间内将产生大量的热能从而导致热失控，进而可能引发火灾或爆炸，造成严重的安全事故[4]。

1.2 锂离子电池的工作原理

LIB的充放电过程是一种理想的可逆反应，这类似于一种物理性质的变化：引起层间距变化却不破坏晶体结构。以石墨为负极，LiCoO2为正极给出电极反应的示例。

正极反应：

负极反应：

总反应：

化学方程式中：LiCoO2为氧化钴锂；x为当前离子数与电池内该离子总数的比值；xLi+为单独锂离子数占电池内总锂离子数的量；Li(1-x)CoO2为氧化钴锂中锂离子数占电池内总锂离子数的量，电池内总锂离子数的量始终为1(假设无损失)；e-为电子；C和C6为石墨；C6Li为石墨层间化合物(类似于图1所示Li嵌入活性物)。

放电时，电子携带电能由外部电路通过负载，为负载供给电能，而后继续由外部负载回到正极。与此同时，失去一个电子的Li将携带正电荷，由储Li粒子内脱去并由扩散机制通过分隔器，进入正极储Li粒子与电子结合；充电过程反应与放电过程相反(可逆反应)。

Li从储Li粒子脱去时，粒子发生一定程度收缩导致活性物质之间空隙增大，Li的扩散和游离速度略微变慢(低温情况下，储Li粒子间液态化学添加剂“黏度”增大，Li的扩散和游离速度下降，但这是暂时的和可恢复的)。这会造成电池管理系统(battery management system, BMS)的电压电流检测值偏低，可能导致BMS做出错误的判断：SOC值过低，为保护电池而阻止电池继续进行放电操作，这是目前纯电动汽车在低温地区续航能力大幅下降和正常启动困难的主要原因。相反，Li由化学添加剂进入到储Li粒子时粒子发生一定程度膨胀，活性物质间的空隙会减小。高温时储Li粒子的膨胀和挤压受应力加剧，可能导致储Li粒子永久性失去一部分储Li能力(电极材料的分解：图1中活性物储存小黑点的方格“破裂”而无法再存储Li)，另外，传统LIB液态的电解质亦会有一定的“损失”，如泄漏或挥发。过充，过放以及温度对LIB的性能均有较大影响[5]，特别的是，过高的环境温度会造成LIB无法恢复的损伤[6]。

2 电池荷电状态的定义

EVs动力电池SOC通常以具有实际可行的工程定义应用为主。2009年，美国先进电池联合会(the United States Advanced Battery Consortium, USABC)定义电池SOC为：一定放电倍率下，电池剩余电量与其额定电量(相同条件下)的比值。计算公式为

(1)

式(1)中：Qresid为电池剩余电量；Q为电池额定电量。

这种简单的能量定义具有实际的应用可行性，但无法阐述清楚电池SOC的具体物理意义。在式(1)中Qresid更严谨的定义应是某电池在一确定时刻所能继续释放电能的量，这个量的值实际上并不完全等于该电池的剩余电量的值。在LIB放电过程中，Li“小黑点”不能100%从活性物质中脱去。并且，过度的放电会导致电池加速老化严重影响电池性能，对电池造成永久性损伤，这是不允许和不合理的。因此，实际Qresid的量与电池绝对剩余电量的比值小于100%；同样，Q更严谨的定义应是某电池可释放电能的总量。文献[3]详细具体地定义了电池SOC的物理意义，并将其物理意义定义和工程意义定义区分开来：由1.2节阐述的LIB工作原理可知，电池通过电子给负载输送电能，Li的带电荷数量即是电池的储电量，若能精确计算LIB一个电极内所含Li的量，则能精确得到LIB的SOC。假设θr为储Li粒子中Li的当前占有率(可近似理解为图2中黑点的量与方格的量的比值)，则LIB的剩余储电量计算公式为

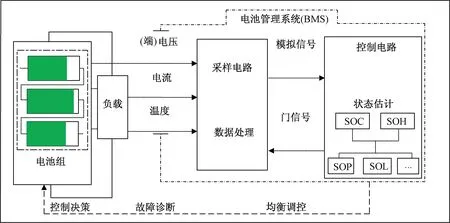
图2 EVs-BMS功能Fig.2 The structures and functions of the EVs-BMS

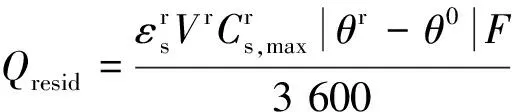
(2)

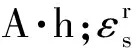
基于此，LIB的总电量计算公式为

(3)

式(3)中：Q为LIB额定(总)电量；θ100为储Li粒子中Li的最高占有率。

式(2)和式(3)中，法拉第常数F可以将代表电量的Li的量的单位由摩尔(mol)转换为安培·秒(A·s)，再转换为安培·小时(A·h)，使之成为更符合EVs动力电池的电量单位。将式(2)和式(3)代入式(1)可得

(4)

这种物理定义从根本上阐述了电池SOC的意义，是简单经典SOC能量定义的具体化。但对于实际的工程应用来说，该物理定义同样存在一个严重的应用问题：θr为储Li粒子中Li的当前占比目前无法计算也无法测量，是一个相对的绝对未知的量(若存在仅由Li组成电池一极的新型锂离子电池，这个物理量在理论上是可以精确得到的)。因此，现阶段仅能通过一些手段对电池的SOC进行“间接估算”，而非“直接计算”。在工程应用上，电池SOC的估算精度误差一般要求控制在5%以内。

3 电池荷电状态的估算方法

准确的SOC估计是BMS高效运行的基础，BMS通过状态估计以控制电池，优化和提升电池性能[7]，如图2所示。

相对早期的传统SOC估算方法一般是通过测量LIB的外部参数直接计算，这一类方法有基于开路电压法(based on open circuit voltage, OCV)、基于电流积分法(based on current-sensor integration, CSI)以及基于阻抗法(based on impedance measurement, IM)等。随着计算机算力的大幅提升，机器学习(machine learning, ML)中的神经网络方法(artificial neural networks, NNs)得以广泛应用，研究人员提出了NNs估算电池SOC的数据驱动的方法，另外还有基于电池模型使用滤波器的估计方法。现在，EVs动力电池SOC一般多采用单一算法的相互融合与改进联合估算。SOC的估计方法分类如表1所示，下面对主要的SOC估计方法进行综述。

表1 EVs动力电池SOC估计方法Table 1 The main estimation methods of the SOC

3.1 基于开路电压

由LIB工作原理可知，当LIB电化学状态平衡时，其外部端电压与LIB电压(正负极电势差)相等。通常情况下，对电池或电池组进行长时间的静置可以使LIB内部化学反应达到平衡状态(OCV的这种特性适用于估计LIB初始状态的SOC值)。LIB的SOC值较高时，放电效率高，电流值与OCV也相对较高；若SOC值较低，OCV值亦随之下降，即SOC与OCV呈正相关。通过实验测量与理论计算表明， OCV与SOC存在对应的函数关系，这种关系会受到LIB所处环境温度影响。图3为5种不同电池在25 ℃时OCV与SOC的关系曲线图，这5种电池的SOC大范围变化时，其OCV变化范围幅度较小：在SOC由10%增至90%的过程中，OCV的变化幅度最大约为0.5 V，最小不足0.1 V。

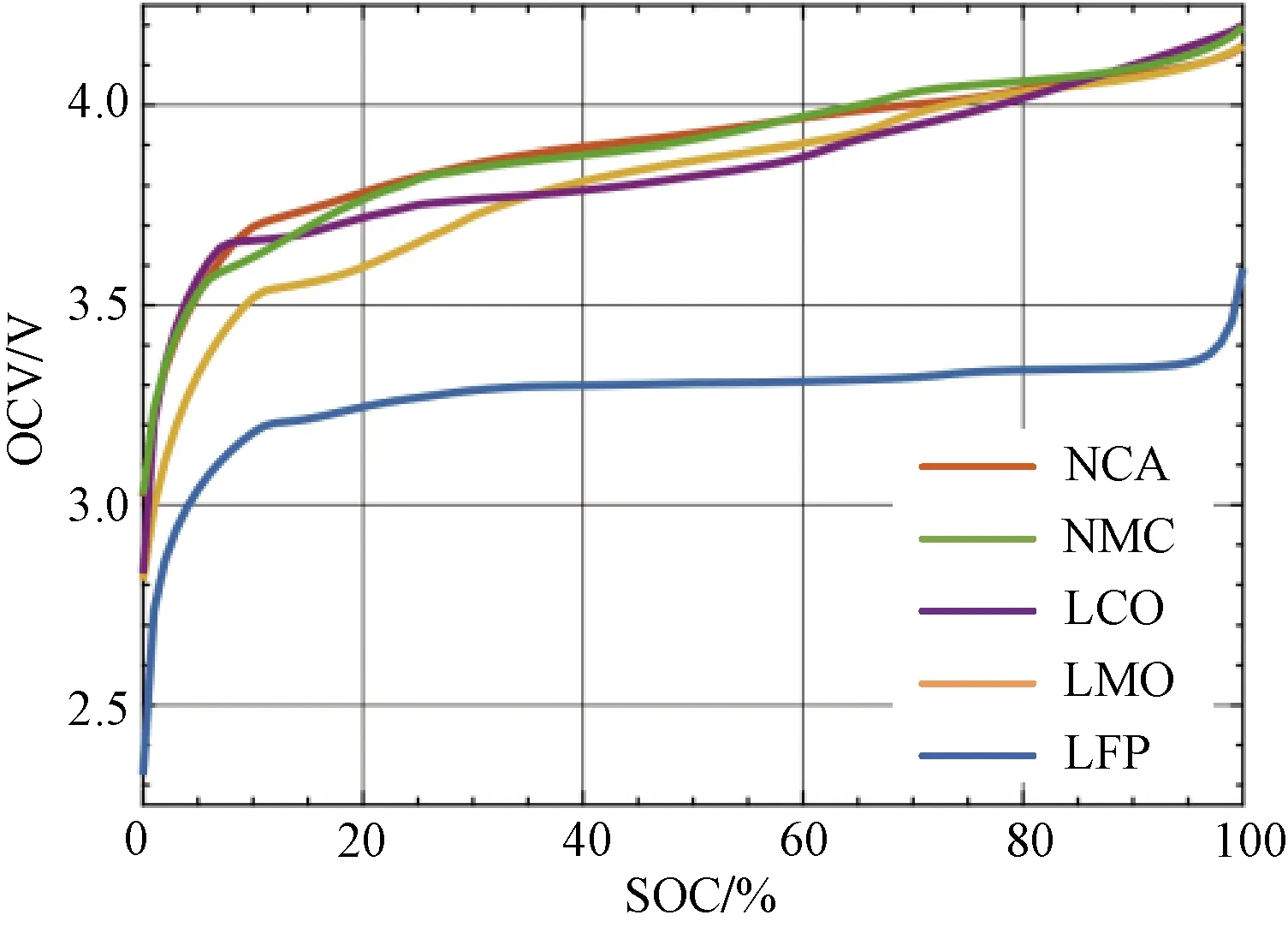
NCA为镍钴铝电池；NMC为镍锰钴电池；LCO为锂钴电池； LMO为锂锰电池；LFP为磷酸铁锂电池图3 25 ℃时5种不同电池OCV与SOC的关系曲线图[3]Fig.3 Examples of OCV versus SOC relationships for ve different lithium-ion cell designs in 25 ℃[3]

在OCV在3.3V附近时，LFP对应SOC区间为30%～90%，这表明若仅通过OCV的单一参数对SOC进行精确的估计是困难的，故OCV往往结合于其他算法共同估计电池SOC[8]。但另一方面，曲线平缓也表明了该电池放电时能给负载提供较为稳定的工作电压，有利于EVs的综合性能发挥。

Xiong等[9]利用等效电路模型建立OCV-SOC曲线关系，通过查表在线实时估计动力电池SOC。该团队建立了电池弛缓效应和动态特性的等效电路模型，并利用带最优遗忘因子的递推最小二乘法(recursive least squares, RLS)对模型参数进行在线辨识，最后通过实验构造了动力电池OCV-SOC关系曲线。在城市实车驾驶验证试验下，该SOC估计方法的最大精度误差控制到了5%以下，满足工程应用。Wang等[10]考虑了温度对OCV-SOC关系的影响，采用了自适应联合卡尔曼滤波(adaptive joint Kalman filter, AJKF)估计模型电路的状态。研究实验证实了OCV与SOC具有强的确定性相互关系(前提是LIB内部化学反应达到平衡状态)，但等效电路模型与EVs动力电池组真实状态仍存在一定偏差[11]。

3.2 基于电流积分

在LIB工作时，对其通过负载的测量电流进行关于工作时间的积分，便可得到LIB在这段时间内所消耗的电量，再用初始状态的电池SOC值减去消耗电量与LIB额定电量的比值，便可得到该电池当前的SOC，这是基于电流积分法估计电池SOC的基本原理。

(5)

im(t)=i(t)+in(t)+ib(t)+is-d(t)+il(t)…

(6)

式(6)中：i(t)为真实电流；in(t)为电流噪声；ib(t)为测量偏差；is-d(t)为自放电电流；il(t)为电流泄漏。

若仅在某瞬时，对单只电芯而言，电流偏差和库伦效率计算偏差对SOC计算结果影响是微小的，但将这些存在偏差的测量计算值对大容量电池组进行以小时为单位的积分，则会造成大量的误差积累，并且这种积累误差很难得到真实的反馈与修正。另外，电池的老化也会减小电池SOC满状态时可释放电能的总量[14]，进一步影响了该方法的计算精度。图4为LIB放电过程中基于电流积分的误差累积示例(未考虑库伦效率变化)。

绿色区域上方为i(t)随时间变化的曲线； 褐红色区域上方为im(t)曲线图4 LIB放电过程中基于电流积分的误差累积示例Fig.4 An error accumulation example based on the method CSI during LIB discharge

在0～t时间内，由于电流随电池SOC降低而相应减小，电流的绝对测量偏差的比率将不断增大，导致积分计算误差不断累积。解决基于电流积分的SOC估算方法误差累积问题的根本性措施除了提高电流测量传感器精度外，还需要考虑对误差进行实时的反馈与修正，以及对不同SOH值的电池(或电池组)应使用不同的库伦效率计算。而EVs动力电池在放电时，温度的变化、EVs的非平稳运行状态(急加速或急刹车情况)和电池的SOH变化都会导致LIB的放电电流产生较大波动(放电倍率不稳定)，同时影响库伦效率的取值。因此，在数学和物理的角度上，对测量电流的积分误差进行精确的修正非常困难。文献[15]提出了一种基于容量修正该估算方法误差的原理：

(7)

式(7)中：ηi为电流倍率修正因子；ηt为温度修正因子；ηh为循环寿命(老化)修正因子。

该方法采用OCV估计电池初始状态SOC值，而后使用CSI进行实时估计。式(7)的算法通过考虑温度、电流波动和电池老化对估计误差的影响，间接“减小”了电流的测量偏差和库伦效率数值的变化，在一定程度上提高了估计精度，但仍然回避了im(t)的根本性问题。单一的CSI方法对于准确估计EVs动力电池SOC来说非常困难[16]，但该方法可与其他算法融合以辅助估计动力电池SOC，且此类融合算法应用较多[8, 17]。

3.3 基于阻抗

电池阻抗一般适用于估计电池的内部温度，间接为BMS提供估计计算电池其他状态的数据基础[18]。使用电池阻抗估计电池SOC需要通过电化学阻抗谱(electrochemical impedance spectroscopy, EIS)实现。将角频率为ω的小振幅单一交流电信号(正弦电流信号)输入某线性或非线性系统，该系统阻抗可表示为

(8)

式(8)中：f(ω)为该单一交流电信号；g(ω)为f(ω)通过系统输出的同频率下的交流电压(电势差)信号。

描绘EIS需要监测由输入信号f(ω)导致输出信号g(ω)的变化，并建立一个相关的数学模型：

Z(ω)=h(ω)ejø(ω)

(9)

式(9)中：h(ω)为f(ω)引起的g(ω)振幅变化量；ø(ω)为f(ω)与g(ω)的相位偏移量。

显然，不同的频率ω会导致产生不同的Z(ω)。文献[19]描述了不同频率对EIS的影响，并在阻抗模型的基础上，引入了分数阶卡尔曼滤波(fractional Kalman filter, FKF)对SOC进行估计。该团队通过实验验证基于阻抗模型的估计方法优于基于RC模型的估计方法，且具有更高的SOC估计精度。文献[20]简化了电化学阻抗谱模型，利用FJKF完成了对磷酸铁锂电池的参数在线估计(通过OCV直接估计该类电池SOC很困难)，在一定程度上为估计此类电池的SOC提供了支持。虽然，基于电池模型的EIS用于估计电池SOC具有确定的可行性，但由EIS的绘制原理发现，该方法仍存在局限性。例如，在由f(ω)输入至感知测量输出信号g(ω)的时间跨度内，LIB的内部化学反应可能会对h(ω)的值产生较大干扰影响，即在监测输出信号的频率响应时，要求LIB处于电化学平衡状态(类似于采用OCV方法估计电池SOC时的要求)。另外，针对高频时建立的复杂模型不仅增加了计算量，还可能无法提高EIS拟合精度[21-22]，并且温度也会对阻抗造成较大影响[23]。

3.4 基于神经网络

人工神经网络诞生于20世纪40年代，目前该方法应用领域广泛，NNs的基本结构如图5所示，这是一种全连接网络。

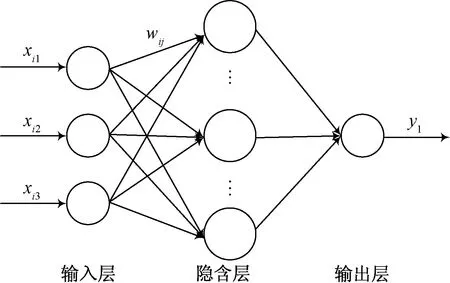
xi1、xi2、xi3分别为电池当前的温度、电压值和电流值； y1为电池SOC值，隐含层的神经元个数并不固定图5 NNs基本结构图Fig.5 The primary structures of the NNs

NNs算法通过搭建函数网络，将输入层参数x赋予不同权值wij(也可能加偏置数)传递到下一个计算层，这些数据再通过激活函数转换后向前传递，最终输出电池SOC(y)值。在NNs的训练过程中，数据有向前和向后两个传递过程，如BPNNs训练时其结果误差会进行反向传播并修正各层网络的权值和阈值，循环执行该过程完成网络的参数最优化学习。卷积神经网络(convolutional neural networks, CNNs)是包含卷积计算且具有深度结构的前馈神经网络，它可以提取输入数据的高层抽象特征，CNNs在计算机视觉领域应用非常成功，但也有学者将其应用于锂离子电池SOC估计[24-25]。

NNs是简单计算概念——复杂计算量的算法：无需大量严谨苛刻的运算规则，但需要庞大的训练数据集对网络模型进行训练，这导致训练的数据样本在很大程度上决定了算法实际应用的精度。Guo等[26]通过优化NNs参数，减小电池模型的计算量以优化NNs估算SOC，从而降低计算成本并提高了不同充放电状态下的SOC估计精度。该研究筛选减小了NNs的输入变量并优化调整了NNs隐含层参数，在一定程度上简化了计算。显而易见的是，网络轻量化操作势必会影响估算精度，但在实时性和估计精度上合理的折中考虑同等重要。Angelo[27]使用5个NNs协同计算，完成了对SOC和SOH的联合估计(对于传统估计方法来说通常是难以实现的)；实验表明，该联合估计状态控制精度误差约为3%，有希望直接运用于BMS。但Angelo[27]实验没有较全面地考虑温度变化影响，设定恒为25 ℃的理想实验温度与实际工作环境温度有较大差别，需要进一步的研究。Ephrem等[28]提出一种深度前馈神经网络(deep feedforward neural networks, DNNs)估计电池SOC的方法，训练好的DNNs可在不同环境温度下对电池SOC有较精确的估计；在-20～25 ℃的温度范围内，其估算平均绝对误差控制在3%内，Ephrem等[28]研究相对来说填补了Angelo[27]研究的不足。

LIB工作过程是高度非线性的，这些研究证实了NNs方法具有强的非线性捕捉能力，可以获得很高的估计精度，但不能忽视其庞大的计算消耗和较低的实时性。另外，NNs在训练参数过多而样本不足时可能出现过拟合的情况；在训练参数过少(模型太简单)时可能出现欠拟合情况。过拟合和欠拟合的NNs模型几乎不能部署于实际应用。

3.5 基于模型

基于电池模型的SOC估计通常采用滤波器类算法实现，滤波器类算法能很好地从一系列包含噪声的数据中估计系统的真实状态，目前用于电池SOC估计的滤波估算方法主要有基于卡尔曼滤波器(Kalman filters, KF)的改进算法和基于粒子滤波器(particle filters, PF)的改进算法。

3.5.1 基于卡尔曼滤波器算法

卡尔曼滤波器算法于1960年由Kalman[29]提出，该算法能很好地应用于线性滤波和预测。现用于电池SOC估计的自适应无迹卡尔曼滤波(adaptive unscented Kalman filter, AUKF)算法[30-31]和自适应扩展卡尔曼滤波(adaptive extended Kalman filter, AEKF)算法[17, 32]等都是基于线性卡尔曼滤波(linear Kalman filter, KF)算法改进而来的，EKF和UKF适用于非线性系统(EKF利用Taylor展开将非线性系统线性化，对于强非线性系统可能失效；UKF采用UI变换在估计值附近得到Sigma点)。式(10)可反映KF算法的基本概念：

(10)

通过前一时刻的估计值和当前观测值更新对系统状态变量的估计，通过Kg赋予预测值和观测值不同的权重，以反映现时刻系统的真实状态。即按照预测-实测-修正的循环顺序递推计算，以达到排除干扰再现系统真实情况的目的。

在式(10)概念解释的基础上，假设有一个线性离散时间系统(线性高斯系统)，该系统的状态空间方程为

xk=Axk-1+Buk+wk

(11)

yk=Cxk+Dxk+vk

(12)

式中：xk为系统当前时刻(k时刻)估计状态；xk-1为系统前一时刻(k-1时刻)估计状态；uk为系统控制因子(通常不需要)；wk为过程噪声；yk为系统观测状态；vk为观测噪声；A、B、C、D为估计和观测系统建模所需的常数或常数矩阵(可能为时变矩阵，一维线性系统时则为常数)。

基于KF算法的计算流程如图6所示。

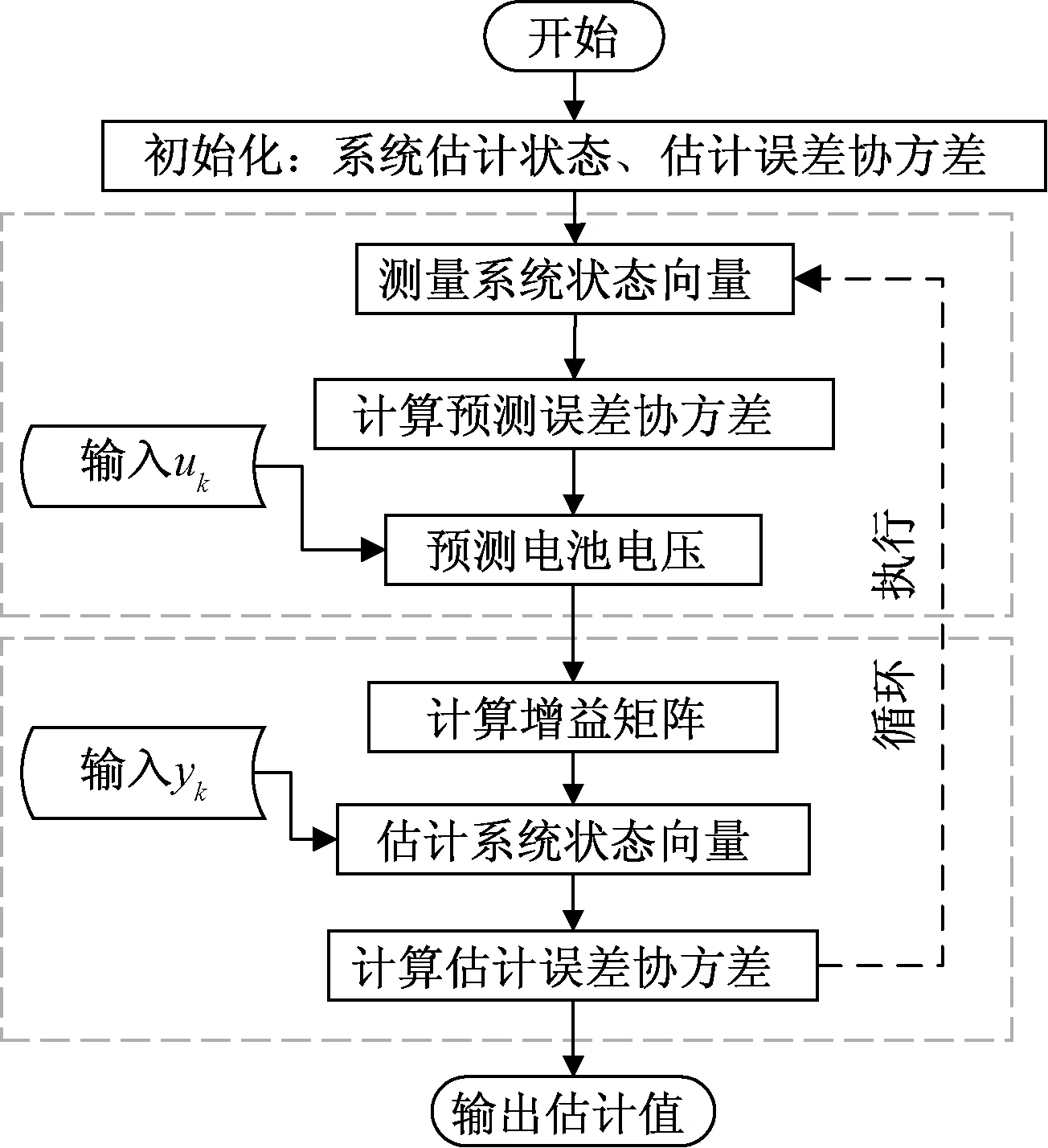
图6 KF算法一般流程Fig.6 The generic steps shared by the KFs

假设估计数据与测量数据的误差服从正态分布，且过程噪声与观测噪声无关(假设为高斯白噪声，但在电流和电压传感器的影响下，噪声可能是非高斯分布的)，并假设有一组观测数据为

Mk=[u0,u1,…,uk,y0,y1,…,yk]

(13)

基于此，对KF算法的仿真示例如图7所示。

图7 KF算法仿真示例Fig.7 An example of the KF algorithm

图7中KF算法仿真显示，通过Kg的数据融合，系统真实估计状态与观测数据和预测数据偏差较小，真实状态估计曲线基本位于xk曲线和yk曲线之间。一定程度上来说，基于KF改进的SOC估算方法解决了NNs计算量较大和可能过拟合的问题，并且同样具有较高的估计精度和鲁棒性，因此是一种现在普遍使用的SOC估计方法。Xu等[19]在阻抗模型基础上，使用分数阶卡尔曼滤波法(FKF)对电池SOC进行估计。分数阶建模方法使阻抗模型能用方程表示，更便于实现动力电池SOC估计。Nguyen等[31]将UKF算法和PF算法相结合，提出了一种UKF-PF的综合估计方法来估计LFP电池的SOC，对比于单一UKF算法，实验表明该估算方法估计精度和可靠性均有提高。文献[33]提出一种新的自适应平方根扩展卡尔曼滤波(adaptive square root extended Kalman filter, ASR-EKF)算法，该算法能消除计算机的舍入误差，较传统EKF算法有更高的SOC估计精度和更好的鲁棒性。文献[34]融合了多种基于KF和PF的算法，并将其用于SOC和SOH的联合估计，提出了一种与文献[33]略有差别的反向平滑平方根体积卡尔曼滤波算法(backward smoothing square root cubature Kalman filter, BSSRCKF)，并在此基础上提出多尺度混合卡尔曼滤波算法(multiscale hybrid Kalman filter, MHKF)，然后又将布谷鸟搜索算法改进并嵌入到粒子滤波算法中(improved cuckoo search-PF, ICS-PF)。BSSRCKF提高了估计精度和收敛速度，ICS-PF优化了规则预测。文献[35]提出一种基于分数阶的自适应扩展卡尔曼滤波(fractional-order adaptive extended Kalman filter, FO-AEKF)估计电池SOC方法，并加入遗传算法优化参数辨识，对比于传统积分阶(integral-order)自适应扩展卡尔曼滤波(IO-AEKF)，FOAEKF有更精确的估计精度。这些研究表明采用多种算法的融合确实可提高SOC估计精度和鲁棒性，但多算法的融合也同时增加了其计算概念的复杂性，不过其计算量仍小于ML类算法。在工程应用上，对于计算量复杂性的考虑通常优于对计算概念复杂性的考虑。

3.5.2 基于粒子滤波算法

PF算法利用一组样本(或称为粒子)近似表示系统的后验概率分布，然后用这种近似表示对非线性系统的状态进行估计。与基于KF算法只能对包括噪声在内的线性高斯系统进行状态估计不同(EKF、UKF等可用于非强线性系统：要求噪声服从高斯分布)，PF几乎可以处理所有形式的概率估计问题，状态方程为

xk=f(xk-1,uk,wk)

(13)

yk=h(xk,ek)

(14)

式中：f(·)为状态转移函数；xk为当前(k时刻)系统状态；xk-1为前一时刻(k-1时刻)系统状态；uk为控制因子；wk为状态噪声；h(·)为观测函数；ek为观测噪声。

PF算法执行过程与KF算法有些相似之处，PF算法为预测-修正-重采样的循环递推顺序。PF通过状态转移方程将k-1时的每个样本(粒子)进行预测，得到与之对应的k时刻的预测粒子，然后通过修正，赋予各粒子不同的权重，再由重采样根据粒子权重进行粒子过滤，以此估计系统的状态(可理解为蒙特卡罗方法附加重要性采样思想)。通过PF算法的执行过程可知，该算法会对每个样本粒子进行预测、修正、筛选和估计，故能获得非常高的精度，但同时也带来了巨大的计算量。Plett[36]采用蒙特卡罗方法(Monte-Carlo method)近似积分减少了PF算法的计算量。图8为PF算法仿真示例。

由图8可以看出，相比于图7的KF算法，PF算法估计值曲线与真实值曲线拟合度更高。PF与KF算法概念复杂性相当，但PF计算复杂性更强计算量更大，对于EVs的BMS来说，实时性是一个重要的考虑因素，故PF算法用于LIB估算时一般会被简化使用[37]。Xu等[38]采用了自适应双粒子滤波估计电池SOC的方法，基于模型，该方法能在电流和温度随时间变化的动态条件下估计电池电压和SOC。对电池SOC进行精确的动态估计是困难的，而采用粒子滤波算法使其动态估计精度达到了96.8%。不过该团队的研究忽略了多时间尺度选择的理论基础和电池的SOH模型，估算方法的精度及鲁棒性还可进一步提高。Liu等[39]基于电化学模型采用PF算法对SOC和SOH进行联合估算校准，并考虑了电池老化的影响。其实验结果表明，SOH范围在70%～100%时，SOC估计精度误差最大为2.8%，但该团队目前还未研究分析温度和电流速率对SOH校准截止电压的影响。Xia等[40]比较了扩展粒子滤波(extended particle filter, EPF)、容积粒子滤波(cubature particle filter, CPF)和无迹粒子滤波(unscented particle filter, UPF)3种估算电池SOC方法的复杂性，准确性和鲁棒性。将该团队对于EPF、CPF和UPF算法相关性质的比较实验研究发现总结为表2(性质评价比较仅相对于粒子滤波类算法)。

由表2可知，估计精度和鲁棒性与算法复杂性呈正相关，若要追求高的估计精度则必然要承受较大的计算量并花费更多的计算时间，BMS设计必须平衡考虑SOC估算方法的综合性能，以提升EVs整体的工作性能。

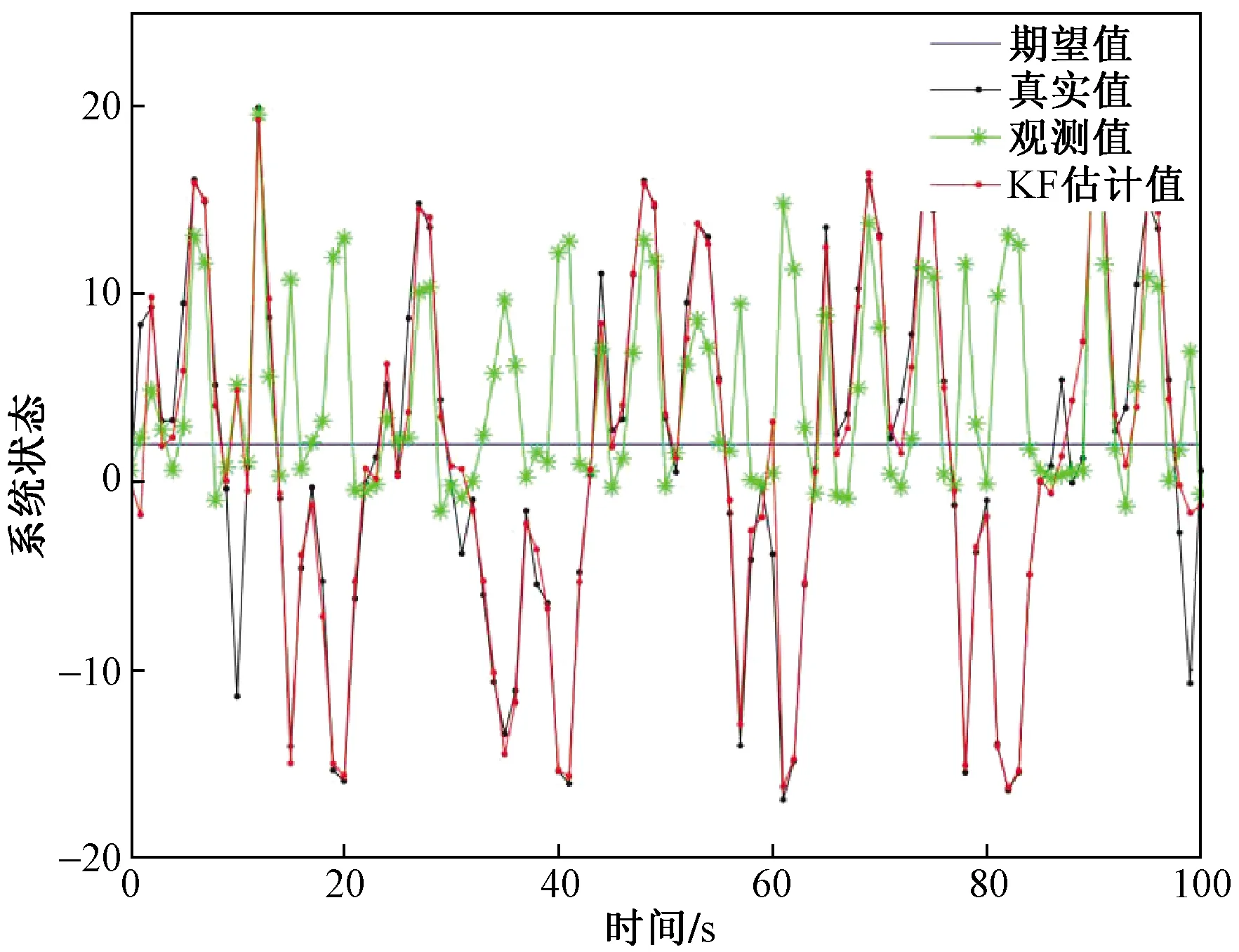
图8 PF算法仿真示例Fig.8 An example of the PF algorithm

表2 不同粒子滤波算法的相关性质比较Table 2 The contrast of different algorithms based on the PF

3.6 其他估算方法

除上述5类SOC估算方法外，还有使用ML的支持向量机算法(support-vector machines, SVMs)、基于滑模观测器方法(sliding mode observer, SMO)[41]和电化学模型或物理模型估计等其他方法以及多种方法的融合[42-46]。Copley等[47]采用了超声波响应以辅助估计电池SOC，较有新意。

SVMs属于一种分类算法，它利用内积核函数代替向高维空间的非线性映射，支持向量(该算法的训练结果)决定了SVMs的最终决策。这种算法以支持向量为基础数据，而不是样本，导致该算法对于大规模的训练样本和多种类的数据划分显得乏力[48]，相对于SVMs算法，NNs和滤波器类算法更适用于SOC估计[49]。

基于电池模型的SOC估计一般用于实验室研究估算方法及测试算法的综合性能，所建立的电池模型精度和可靠性是该类估计方法的关键。电池模型可以在相当程度上模拟电池的真实状态，但其概念和推理过程复杂，建立一个准确可靠，能反映真实电池状态的电池模型比较困难。LIB的SOC估计通用等效电路模型(equivalent circuit model, ECM)如图9所示。在图9中，电压源模拟OCV与SOC的相互关系；R0模拟LIB等效串联电阻；电容Ci与电阻Ri(理论上i的取值为1～n)并联后以子电路形式串联接入主电路，以模拟Li的扩散机制(与时间有关);V-H为一非线性元器件，以模拟电压迟滞效应，这些用于模拟的电子元器件假设为理想元件。采用基于等效电路模型对电池SOC的估计方法多是基于该ECM的不同程度简化：仅由电压源和R0组成的等效电路模型称为Rint模型；在Rint模型基础上，串联接入一个并联电容电阻子电路的模型称为Thevenin等效电路模型(或一阶RC模型)；在Thevenin模型基础上，再接入一个电容电阻子电路为二阶RC等效电路模型。模型的复杂性与模拟精确性呈正相关，复杂模型对电池动态特性模拟更为准确[50]，但其带来困难的参数识别，可能不适用于工程应用[51]。

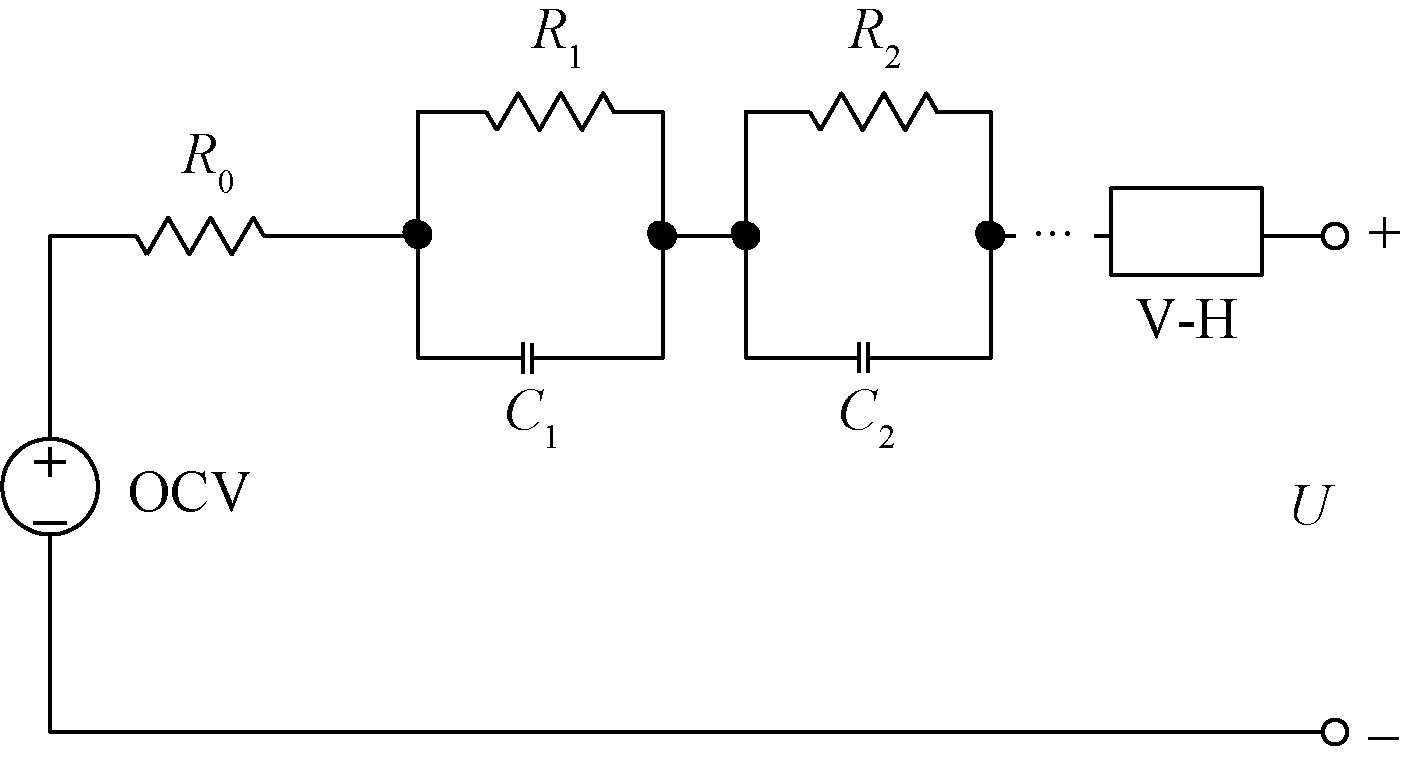
图9 LIB等效电路模型Fig.9 An equivalent-circuit model of the LIBs

大量学者使用了基于模型的电池SOC估计方法[9,17,38,52-57]，它综合了基于数据驱动法的估计精度高和基于传感器测量法计算量小的优点。但该方法仍存在一些关键性问题还有待进一步研究，如物理电池模型无法反映电池内部化学状态，而电池内部化学反应却是决定电池性能(SOH, SOL, …)最基本的因素之一。

4 讨论与展望

EVs动力电池SOC估算属于工程应用研究，其最终目的是将算法部署于实车之上。然而，当前实际应用仍以CSI和OCV等传统方法估算SOC为主，尽管这些方法存在诸多局限性，如精度低和鲁棒性差。而多数新的“优秀”算法停滞在实验室阶段[9](包括但不限于NNs和基于物理及电化学模型方法等)，由前文对各类SOC估算算法实现原理分析可知，造成这种现象的原因主要有以下几点。

(1) NNs方法。当前的人工智能研究发展属于弱人工智能(artificial narrow intelligence, ANI)阶段，这决定了该方法差的泛化性：针对不同的电池型号需要不同的训练数据集。此外，一个性能均衡的NNs模型的参数量通常以百万或千万个为单位：无论是训练阶段还是预测阶段，对算力要求都极高，耗能。而新能源智能车的车载计算平台算力往往非常有限，并且这些算力还要服务于辅助驾驶的NNs计算。

(2)基于模型的方法。LIB是一个高度复杂的非线性时变系统，建立一个能较好反映真实电池状态的模型异常困难。并且，耗费大量时间成本建立的复杂模型虽然能较好模拟LIB动态特性，但是其困难的参数识别使得SOC估算算法亦难为无米之炊。

(3) 融合类算法。多种算法的合理融合能显著提高SOC估计精度和鲁棒性，但不能忽视的是融合算法在综合了不同算法的优点的同时，亦不可避免地引入了不同算法其本身的缺陷。融合类算法的研究者们也鲜有明确地提出其算法实时性与原算法的比较，过度追求精度而损失速度不可取。考虑实际车载计算平台算力，将二者合理折中不失为一种明智之举。

(4)研究与应用对象差异。当前的SOC估算研究大多基于单体电池，而EVs工作需要的大功率和高电压使得其必须使用电池组(电压过高会直接击穿电池分隔层，单体电池串联可减小其承受电压，保证工作安全)。电池组SOC估计与单体电池SOC估计存在显著差别，在相同环境和工作条件下，电池组内各单只电芯的SOC也可能不尽相同[58]，如图2所示。电池组SOC值并不等同于单只点芯SOC值，这无疑将导致电池组内单只电芯的过充或过放情况发生，使得单只电芯过早老化从而影响整个电池组性能，见1.2节所述。此外，汽车的真实工况极不稳定。就中国地区来说，城市与农村路况、南北和东西部气候与温度等差异巨大，EVs工作范围不可能也不能仅局限于一个城市和地区，于温和环境实验室内仿真实验评估出来的SOC估算算法的实际鲁棒性和精度还有待考量。

总体而言，SOC估算研究成果应用于工程实际还存在一定困难。对于NNs类算法，参考不同领域的新的网络模型进行网络轻量化相关研究是一种好办法；基于模型类的方法相关基础研究仍处于较早阶段，它类似于数字孪生系统，是一项充满机遇与挑战的研究；融合类算法极为灵活，且当前该类研究方法的发文量最多，通过大量实验合理融合优秀算法可以获得很好的估算效果；对于电池组单内只电芯SOC值差异而造成的电池组SOC估算难题，结合电池SOC值均衡策略可有效缓解，且此类研究目前也较多。

另外，动力电池SOC估算研究与电池本身的发展密不可分。硅基阳极的LIB具有更高的能量密度，储电能力可达碳基阳极LIB的10倍，但硅基负极在充电时会出现粉化情况，循环寿命极短[59]，而且传统LIB具有液态的电解质，导致电池具有不稳定因素，在电池受到剧烈撞击和结构性破坏时可能引发严重的安全事故。SLMB比传统LIB结构更紧凑，无液态电解质，具有更高的能量密度、安全性和可靠性，是锂离子电池未来的研究趋势[60]，它甚至可仅有正极和隔离层(无储Li粒子负极，工作时阳极全由单一的纯的锂离子组成)，如图10所示。

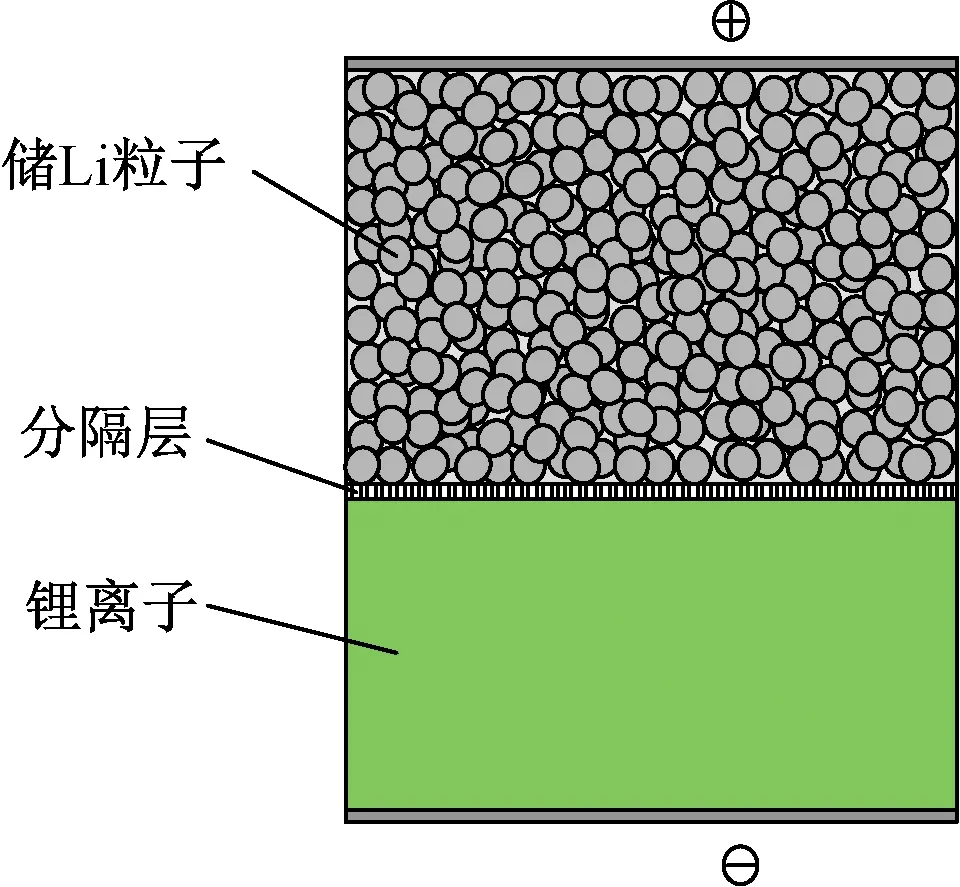
图10 无储Li粒子负极全固态锂离子电池结构Fig.10 The structures of the SLMB cathode without particles

当前对于SLMB的相关研究非常多，对于锂离子电池SOC的物理定义或许能为这种新的锂离子电池SOC精确计算提供理论支持。

5 结论

阐述了锂离子电池的物理工作原理，综述了电动汽车锂离子动力电池的荷电状态估计方法并进行了比较。分析指出，EVs动力电池SOC估算的新研究应用于工程实际仍存在一些困难。基于此，SOC估算未来研究应关注实际工程应用，并联系LIB发展触及其物理本质，以望为未来新型动力电池状态估计提供更优的解决方案。