柔性X－Y－Z－θz四自由度位移传感器的静态解耦方法研究*

祖洪飞潘 奔彭来湖

(浙江理工大学机械与自动控制学院，浙江 杭州 310018)

近年来，各国先进装备制造、智能机器人和现代化工业生产等领域正蓬勃发展，这些领域对多自由度高精度位移传感器的需求也在逐步攀升。同时，为了满足不同应用场景以及各种复杂工况下的测量要求，研究者们也在不停地对位移传感技术进行革新，不断有新材料以及新方案的应用[1－2]。多自由度位移传感器是一种可检测到多个自由度位移信息的位移传感器，在现代工业测量领域以及实际科研应用中起着至关重要的作用[3]。理想情况下，多自由度位移传感器每一通道上的输出都只由该方向的位移决定，各通道的输出互不干扰，也没有耦合。但实际上，由于结构设计、机械制造、材料加工及实验测试等过程中存在或多或少的误差使各个通道之间存在不可避免的耦合[4－6]。要提高多自由度位移传感器的测量精度，需最大限度地降低各个参数之间的耦合，并对存在的耦合进行有效解耦[7]。

常用的解耦方法有硬件解耦和软件解耦两种。硬件解耦是从测量原理出发，通过对传感器结构进行优化设计，或通过工艺改良、提高加工精度等手段来减小耦合误差。但是，在实际应用中，硬件解耦往往受到很多因素的制约，如依赖高精密加工装备、工艺流程复杂、成本较高等，因此其应用很受限。不同的是，软件解耦是通过采用一定的解耦算法对测量信号进行数据处理来降低耦合误差的。相较于硬件解耦，软件解耦既不要求精密装备，又不涉及传感器结构及工艺等方面的优化，具有更高的可操作性，从而被广泛采用[8－10]。

本文将从软件解耦的思路出发，对实验室所研究的的柔性X－Y－Z－θz四自由度位移传感器进行静态解耦方法研究及实验测试。由于该传感器所采用的材料为弹性很大的聚氨酯材料，且在测试过程中其各自由度均有较大行程，因此各方向耦合较严重，且存在较大的迟滞以及非线性。本文拟采用对传感器正反行程分别进行静态解耦的方式解决迟滞问题。另外，通过对比分析基于克拉默法则、基于求解广义逆矩阵等常用的静态线性解耦算法，并在基于耦合误差建模的静态线性解耦模型的基础上提出静态非线性解耦模型，从而得到三者之中更适用于四自由度位移传感器的解耦算法，提高传感器的测量精度。

1 传感器测量原理及耦合误差分析

本文所研究的柔性X－Y－Z－θz四自由度位移传感器的测量原理如图1所示。传感器核心部分为具有多自由度和连续大变形能力的圆柱状聚氨酯弹性体，其一端固定，另一端自由，近固定端按一定的规律排布应变片。当移动端产生X、Y、Z、θz方向的位移时，其固定端会产生相应的应变，进而可以通过固定端应变的测量来实现对移动端位移的监测[11]。

图1 柔性四自由度位移传感器测量原理简图

理想情况下，该柔性X－Y－Z－θz四自由度位移传感器每个通道的应变只由对应方向的位移决定。但由于其各自由度位移间存在无法避免的耦合，致使传感器最终输出的对应各自由度的位移是多维耦合的结果，而非与各自由度一一对应。即每个自由度的位移都或多或少会对其他维度位移的输出信号产生影响，这严重影响了传感器的测量精度[12－13]。

该传感器的多维耦合误差主要源自以下三个方面。①材料及结构方面:为增大位移测量范围，传感器采用了高弹性、非线性的聚氨酯材料，且为了满足扭转维度的测量需求，传感器采用了简单的圆柱体，结构上并未进行解耦设计；②各轴运动方面:实际上，传感器移动端由法兰盘与机械手连接，产生位移后始终与固定端平行，这与图1所示的弹性体纯弯曲变形情况存在一定的差异。产生位移X、位移Y时，机械手会给弹性体一个轴向附加力，这将对位移Z的输出产生影响。另外弹性体在产生位移Z时，会附加弯曲变形，又会对位移X、位移Y的输出产生影响；③应变片布片方面:近固定端会排布12个应变片，其粘贴位置及角度的偏差也会带来耦合误差。

图2为X、Y、Z、θz四个位移参数单独作用时四个通道的应变输出情况，(a)、(b)、(c)、(d)分别代表仅有位移X、位移Y、位移Z以及位移θz单独作用时，由应变测量得到的各位移输出结果。在无耦合情况下，当仅一个位移单独作用时，其他维度位移的应变输出应为0，即其曲线应平行于x轴且对应应变均为0。但由于多维耦合误差的存在，使其他维度位移的应变输出不为0，甚至有的偏差较大。例如，图2(a)代表仅位移X单独作用，可以看到，位移Z的输出也会随着X方向位移的增大而变大，X位移为30 mm时，Z通道的耦合输出高达577με，这给传感器带来极大的测量误差，故需使用合适的解耦算法对传感器进行解耦。

图2 位移X、Y、Z、θz单独作用时各方向的输出情况

2 传感器的静态解耦方法

传感器常用的静态线性解耦方法主要有三种，分别基于克拉默法则、求解矩阵广义逆及耦合误差建模[14－15]。这三种方法主要用于静态线性解耦，可以解决一部分线性耦合问题，但本文所研究的传感器有存在一定的非线性但不是很严重。由于在耦合建模的线性基础上更易于推导出相应的非线性模型，因此，本文在基于耦合误差建模的静态线性解耦模型的基础上提出了静态非线性解耦模型，通过理论分析以及与其余两种静态线性解耦算法的结果进行对比看是否适用于传感器。另外，传感器正反行程存在一定的滞回，故需对其正反行程分别进行解耦。

2.1 基于克拉默法则的静态线性解耦算法

设四自由度位移传感器位移输入量与应变输出量有良好的线性关系，用位移向量S＝(S XS YS Z

SθZ)T表示任意位移，ε＝(εXεYεZεθZ)T表示任意位移作用下四个位移通道输出的应变值，则输入位移S与输出应变ε满足以下关系:

式中:S为广义位移向量，C为4×4的解耦矩阵，ε为应变输出向量。

选取四个线性无关的位移向量组成标定位移矩阵B；把多次标定实验的位移数据以及对应位移通道的正反行程应变输出数据取平均值，相应位移向量构成的正反行程应变输出为矩阵A；则可通过求解线性方程组的方式求出解耦矩阵C正、C反。以正行程为例:

式中:i、j＝1、2、3、4；S i表示在第n次加载实验中第i号广义位移值的大小，εi j表示第i号广义位移在第n次加载过程中第j号电桥的应变输出量，将标定实验数据分别通过式(2)、式(3)求出矩阵B、矩阵A。则矩阵C正可由下式求得:

针对本传感器的测试及结算结果如下:

同理可求得C反:

2.2 基于求矩阵广义逆的静态线性解耦算法

同样，设四自由度位移传感器位移输入量与应变输出量呈线性关系，且X、Y、Z、θz四个位移产生的变形可叠加。向量S与向量ε与上文意义相同。以传感器正行程为例，当S X单独工作时，传感器四个通道对应的应变输出分别用εX X、εYX、εZX、εθzX，其中εYX、εZX、εθzX分别代表在仅有位移X作用时位移Y、位移Z以及角位移θz的耦合输出，其他εi j的意义可依次类推。那么，根据传感器位移输入与应变输出呈线性的假设可知:

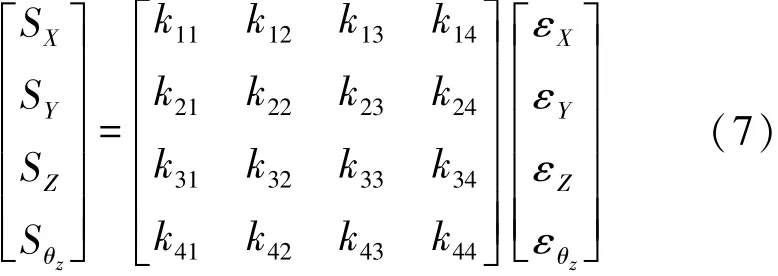
则当S X单独作用n次时可表示为:

当S Y单独作用n次时可表示为:

当S Z单独作用n次时可表示为:

当Sθz单独作用n次时可表示为:

将S X、S Y、S Z、Sθz共计实验n次的结果按式(8)至式(11)整合成如下矩阵表达式:

简记为:

式中:S为4×n的位移矩阵，ε为4×n的应变输出矩阵，K为常数矩阵，则常数矩阵K可由下式表示:

因此，由标定实验中正行程的30组数据(每组数据都为实验3次的平均值)以及相应四个通道的应变输出可构成矩阵S和矩阵ε，其中，S为4×30的位移矩阵，ε为4×30的正行程应变输出矩阵。进而将矩阵S、矩阵ε代入式(14)中求出正行程的解耦矩阵K正:

同理可得到反行程的解耦矩阵K反:

2.3 基于耦合误差建模的静态非线性解耦算法

如前文所述，在四自由度位移不存在耦合的情况下，某一通道的应变输出只由该维作用位移确定，并不受其他位移的影响。如图3所示，ε1、ε2、ε3、ε4表示位移X、Y、Z、θz的输出应变。

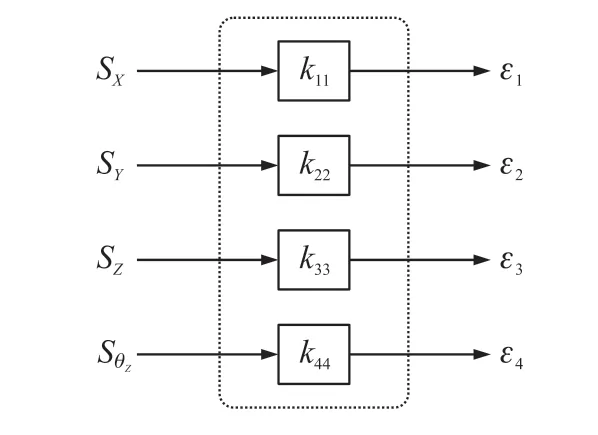
图3 无耦合时四自由度位移传感器输入输出系统

图3所示关系可用下式表达:

在存在耦合的情况下，为了描述方便，这里我们先假设各位移之间的耦合为线性关系，如图4所示，四个通道的应变输出ε1、ε2、ε3、ε4由四自由度作用位移S X、S Y、S Z、Sθz叠加而成，可用如下表达式表示:

图4 存在耦合时四自由度位移传感器输入输出系统

式中:εii代表主方向作用位移对该方向应变输出的影响，εij(i≠j)代表其他位移对该方向应变输的影响。

以S X为例，该方向位移的耦合误差为ε′X＝ε12＋ε13＋ε14，由式(17)、式(18)可知，四自由度位移输入与相应的应变输出满足下式:

令k i jk′jj＝k′i j，可得四自由度的解耦公式为:

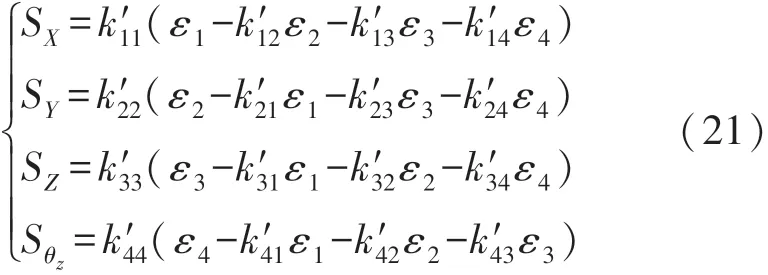
式(21)为基于耦合误差建模的静态解耦算法的基本模型，但该模型是在位移输入与应变输出呈线性这个假设下得到的。然而实际情况是它们之间的耦合并不是完全的线性关系，有的甚至非线性较强，如图5所示。

同样以正行程为例，图5中(a)、(b)、(c)、(d)为四个位移单独作用时，其他三个通道应变的耦合输出与主通道应变输出的关系。可以看出，其关系并非线性。因此，为进一步提高传感器的测量精度，需要一种非线性解耦算法。基于耦合误差建模的静态解耦方法，本文提出了改进的非线性解耦方法，并进行了实验验证，具体如下:实验测试时，分别对传感器施加位移S X、S Y、S Z、Sθz，并记录其余通道的应变输出值，多次试验取平均值，并将四个主通道的位移－应变输出拟合曲线关系用二次多项式表示:

图5 某位移单独作用时其他位移耦合输出与主位移应变关系

则可得到基于耦合误差建模的非线性解耦模型表达式:

然后，根据此基于耦合误差建模的静态非线性解耦算法，将正反行程实验数据代入式(23)、式(24)可求得解耦模型中正反行程各参数方程，见表1、表2。

表1 正行程各参数方程

表2 反行程各参数方程

3 误差对比及解耦结果

为了更加直观地看出三种解耦算法的解耦结果，本文根据三种解耦算法对所测得数据进行解耦，然后由作出相应的绝对误差对比图，如图6至图9所示。

图6 位移X正反行程三种解耦算法误差对比

图7 位移Y正反行程三种解耦算法误差对比

图6至图9分别代表位移X、位移Y、位移Z、角位移θz正反行程采用三种静态解耦算法后的绝对误差对比图，其横坐标为相应位移值，纵坐标为解耦后的绝对误差。由图6至图9可知，在采用基于耦合误

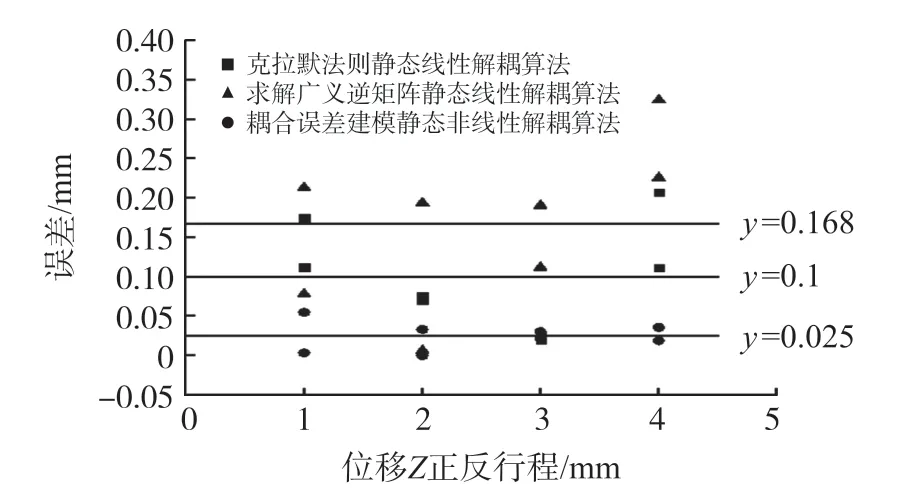
图8 位移Z正反行程三种解耦算法误差对比

图9 角位移θz正反行程三种解耦算法误差对比

差建模的静态非线性解耦算法后，位移X、Y、Z、θz的误差值均明显低于其余两种解耦算法。X、Y、Z、θz四个位移采用基于耦合误差建模的静态非线性解耦算法后的误差均值分别为0.322 mm、0.330 mm、0.025 mm、0.18°。其余两种静态解耦算法的绝对误差值都大于基于耦合误差建模的静态非线性解耦算法的绝对误差均值，这说明基于耦合误差建模的静态非线性解耦算法更适用于本文所提到的四自由度位移传感器。

为了评价四自由度位移传感器的精度，我们用Ⅰ类误差和Ⅱ类误差来表示。

式中:Y i(FS)表示i方向可施加位移的满量程值；e i(max)表示i方向施加的位移值与实际测得位移值之间的最大差值；Y ij(max)表示当j方向施加位移时且其余3个方向无位移时，i方向测得的最大位移。

根据式(25)、式(26)求得四个位移参数未采用耦合误差建模解耦前的Ⅰ类误差分别为1.79%、1.98%、1.37%、1.08%，解耦后分别为1.41%、1.85%、1.25%、1.03；Ⅱ类误差未解耦前分别为6.78%、4.01%、21.42%、3.61%，解 耦 后 分 别 为1.73%、2.05%、1.33%、1.19%。从以上数据可以看出Ⅰ类误差解耦前后变化不大，但Ⅱ类误差降了大约2～16倍。因此，基于耦合误差建模的静态非线性解耦算法显著提高了四自由度位移传感器的精度。

4 结论

本文针对柔性X－Y－Z－θz四自由度位移传感器各维位移因耦合较大而影响测量精度的问题，通过对三种常用解耦算法的分析比较，得到了适用于四自由度位移传感器的解耦算法为基于耦合误差建模的静态解耦算法，并在其线性的理论基础上推导了适合四自由度位移传感器的非线性模型。

另外，针对传感器迟滞较大的问题，本文采用了正反行程分别解耦的方式。

结果表明，在使用基于耦合误差建模的静态非线性解耦算法后Ⅰ类误差虽前后变化不大但Ⅱ类误差降低了大约2～16倍，提高了四自由度位移传感器的精度。

另外，还可通过提高耦合误差建模解耦算法中的函数阶次来进一步提高测量精度，但这是比较有限的。改进解耦算法以及数据修正等方法是今后可考虑的提高测量精度的途径。