基于PF系数的多模态EEG-FNIRS通道选择方法*

孟 明戴橹洋马玉良高云园

(杭州电子科技大学自动化学院，浙江 杭州 310018)

脑机接口(Brain-computer interface，BCI)提供了人类中枢神经系统与计算机之间的直接通信渠道。所以，在不使用肢体，声音或任何需要肌肉活动动作的情况下，BCI可以分析与预期动作相关的大脑感应信号，从而生成控制外部设备的命令[1]。

BCI系统中，常见的信号采集成像方式有脑电图(Electroencephalogram，EEG)[2]，皮层区脑电图(Electrocardiogram，ECoG)[3]，功能性近红外光谱(Functional near-infrared spectroscopy，fNIRS)[4]，功能磁共振成像(Functional magnetic resonance imaging，fMRI)[5]和脑磁图(Magnetoencephalography，MEG)[6]等。其中EEG是一种生物电成像方法，利用头皮电极来测量由大脑皮层神经元的电活动引起的电压波动。EEG具有较高的时间分辨率，频域特点突出，便捷安全等特点[7]。由于电极测量大脑表面的电活动，难以确定EEG信号是在表面附近还是在更深的区域产生的。因此导致EEG空间分辨率相对较低并且容易受到来自肌电和眼电的干扰，导致EEG获得的分类精度明显下降。fNIRS是一种光学成像方法，可评估大脑中的血液动力学活动。fNIRS可测量脱氧血红蛋白(Deoxyhemoglobin，HbR)和氧合血红蛋白(Oxyhemoglobin，HbO)的浓度变化[8]。fNIRS具有相对高的空间分辨率、便携、便宜、抗运动干扰等特点。但是由于血氧浓度反应迟缓，因此导致fNIRS的时间分辨率很低。

EEG与fNIRS都用于多种BCI系统中，以检测例如运动想象，心理算术(Mental Arithmetic，MA)和n-back任务这些源自认知和心理任务的大脑活动变化[9]。由于每种神经影像学方法都有其特定的局限性。在过去的几年中，研究人员一直在努力提高信息传输率并克服单模态系统的局限性，从而形成了多模态系统，称为多模态BCI。

Fazli等人[10]结合EEG和fNIRS对想象左右手抓握进行了实验，结果表明，相比于单模态，多模态BCI可以显著提高90%以上受试者的运动想象分类准确性。Pietro等人[11]对阿尔兹海默症的四种症状进行分类，结果表明与单模态实验相比，EEG-FNIRS通过整合其互补特性能够实现更高的准确性。有研究认为多模态BCI通过增加大脑生理信息量和维度会产生更好的鲁棒性和分类准确性[12]。许多其他研究[13－15]也已经证实EEGFNIRS组合可以增强信号强度，提高分类精度并克服大多数单模态的局限性。多模态BCI系统可以增强分类精度，但是由于系统模态的增加会导致信号维度增加，为减少多模态BCI系统计算负担，对信号进行降维十分必要，如主成分分析(Principal component analysis，PCA)和公共空间模式(Common space pattern，CSP)。除此之外，保留并突出单个模态系统的有利特征对多模态BCI系统的分类性能也有很大提升。Jing Jin等人提出了一种基于Pearson相关系数的通道选择方法，并在左右手分类实验中取得了较好的分类结果[16]；Alborz等人为了确定每个fNIRS通道在信息区分中的作用，计算每个特征的Fisher值，描述fNIRS通道区分信息的能力[17]。但是基于Pearson相关系数的通道选择方法仅考虑了数据之间的相关性，而基于Fisher值的通道选择方法仅考虑了不同任务特征的可分性。这两种通道选择方法并未同时考虑信号相关性和特征可分性。

针对于上述问题，本文提出了一种基于PF(Pearson-Fisher)系数的通道选择方法。将表征信号间相关性的Pearson系数与表征特征间可分性的Fisher值相结合，构建一种兼顾信号相关性和特征可分性的PF系数。此外，为了验证PF系数的优势，本文分别使用基于Fisher、基于Pearson和基于PF系数这三种通道选择方法对MA数据集进行分类对比实验。

1 方法

本文首先选取合理的时间窗数据进行通道选择；然后对已经通道选择的时间窗数据进行特征提取，其中EEG提取CSP特征，fNIRS提取平均值和峰值这两类统计特征；最后通过SLDA进行分类。具体系统框图如图1所示。

图1 基于PF系数通道选择的多模态BCI系统框图

1.1 基于PF系数的通道选择

1.1.1 通道选择的特征

EEG数据的特征主要有三种:时域特征、频域特征与空域特征。小波分析[18]可以提取EEG的时频特征，熵能对系统的状态进行表征。小波熵则结合了小波理论与熵原理的特点，考虑了各尺度能量的分布差异，通过各尺度的信息来反映信号的特征。设信号x(n)经过小波变换，在第j分量尺度下k时刻的高频分量系数为D j(k)，低频分量系数A j(k)，信号x(n)可表示高频分量与低频分量之和，即:

设E＝E1，E2，…，E m，为信号x(t)在m个尺度上的小波能谱。则在尺度域上E可以形成对信号能量的一种划分。由正交小波变化的特性可知，在某一时间窗内的信号总功率因此第j个尺度上的能量概率p j为:

式中:E j为第j个尺度上的能量，于是定义相应的小波能量熵W EE为:

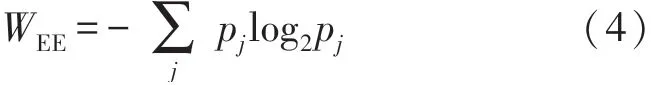
fNIRS的特征提取[19]通常采用信号斜率(signal slope)，信号均值(signal mean)，信号方差(signal variance)，信号峰值(signal peak)，信号峰度(signal kurtosis)和信号偏斜(signal skewness)。

本文采用数据段上每个通道HbR和HbO浓度的平均值(mean)和峰值(peak)来建立特征向量。

①信号平均值(M)

HbO和HbR的浓度平均值计算如式(5):

式中:N是采样点数，X i表示HbO或HbR数据。

②信号峰值(P)

信号峰值是时间窗口中信号的最大值。

式中:X i为采样点i对应的信号电压值。

1.1.2 基于PF系数的通道选择步骤

在多模态BCI研究中，通道选择被视为直接影响系统性能的关键因素。因此，本文提出了一种新颖的方法，通过使用PF系数选取最优的通道来确保实现最佳性能。

Pearson相关系数基于统计分析，其可以分析量化两个通道之间的线性关联的强度，Pearson正值越大表示正相关越强，Pearson负值越大则表示负相关越强[20]。第三种可能性是变量之间不相关，即ρ＝0。给定两个通道[i，j]，相关系数定义如下:

式中:μ代表平均值，σ代表标准偏差，E代表期望算子。

Fisher准则是一种将高维参数投影成一维来测量类判别属性的统计量参数[21]，Fisher值代表了两类样本的可分程度，Fisher值越大表示可分性越强，Fisher值越小表示可分性越弱。给定两个类别样本X－和X＋，相关系数定义如下:

式中:mean(·)为均值，var(·)为方差。

根据PF相关系数代表通道与任务之间关联强度的算法流程图如图2所示。

图2 PF算法流程图

首先分别对EEG与fNIRS构建用于通道选择的PF系数，并根据PF系数设置合理阈值m来确定通道数目，m值越大选择得到的通道数目越少。

(1)Fisher通道选择:

①提取EEG信号小波熵WEE(Wavelet Energy Entropy)特征；提取mean和peak作为fNIRS特征。

②计算EEG与fNIRS每个通道的Fisher值，由通道Fisher值构建列向量，分别记为:EFisher，FFisher。

③对列向量EFisher与FFisher进行归一化，分别记为:IFisher，JFisher。

(2)Pearson通道选择:

①分别构建EEG与fNIRS通道之间的相关系数矩阵。

②选择相关系数最大的EEG与fNIRS通道。

③统计所有试验EEG与fNIRS每个通道的投票数，由通道投票数构建列向量分别记为:EPearson，FPearson。

④对列向量EPearson与FPearson进行归一化，分别记为:IPearson，JPearson。

(3)PF通道选择:

①EEG与fNIRS的PF系数分别为

式中:c为PF通道的权重系数。

②将IPF与JPF中的通道系数阈值设置为mi和m j，根据阈值选择EEG和fNIRS通道。

1.2 特征提取

对通道选择后信号进行特征提取，其中EEG信号提取CSP空域特征，fNIRS信号提取平均值和峰值两种统计特征。

CSP[22]是一种对二分类任务下的空域滤波特征提取算法，能够从多通道的EEG数据里面提取出每一类的空间分布成分。记X1和X2为两类任务下的信号矩阵，构造空间滤波器；首先求信号矩阵协方差，并归一化，得到:

式中:trace(·)为矩阵的迹，然后求出混合空间的协方差矩阵R，并进行特征值分解:

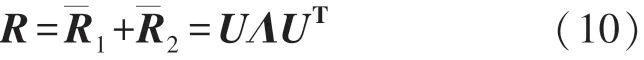
式中:¯R i为两类任务实验的协方差矩阵，i＝1，2，U为矩阵R的特征向量，Λ为对应的特征值矩阵；可以求出白化矩阵P:

接着对R1与R2做白化处理以及主成分分解:

则矩阵S1与矩阵S2的特征向量相等，即B1＝B2，且Λ1＋Λ2＝I，其中，I为单位矩阵。两类矩阵的特征值之和为1，因此当一类的特征值最大时另一类最小，从而可以实现区分的作用。构造空间滤波器W:

将上述原始运动想象信号矩阵X经W滤波，得到Z:

接着取其前m个和后m个特征值构成空间滤波信号Z p，P＝1，…，2m，求取特征向量:

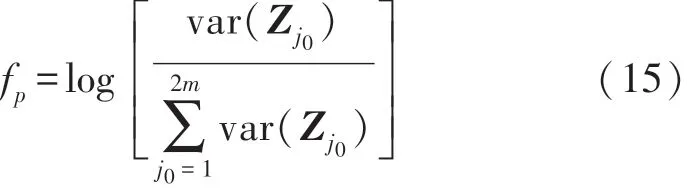
式中:Z j0为空间滤波信号Z p的第j0行信号。

将EEG和fNIRS提取的所有特征分别在0和1之间缩放，x′为重新缩放特征值:

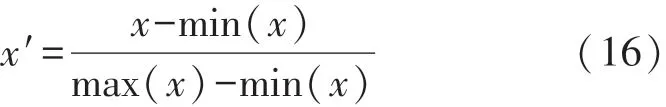
式中:x∈R n表示原始特征值，x′表示介于0和1之间。

1.3 分类

使用收缩线性判别分析(Shrinking linear discriminant analysis，SLDA)方法进行心算任务与静息状态二分类。在训练样本数量比特征数量少的情况下，收缩(Shrinking)是改进协方差矩阵估计的一种方式。通过采用基于Ledoit-Wolf引理的收缩参数，该方法可缓解由于使用高维特征向量而导致的分类精度损失[23]。

2 实验

2.1 数据描述

本文使用由柏林工业大学Shin等人所建立的公开数据集[24]，验证所提出的方法。数据集包含从29位健康受试者(14位男性和15位女性，平均年龄28.5±3.7)收集的EEG和fNIRS信号。EEG系统的采样率为1 000 Hz。EEG采集电极位置由AFp1，AFp2，AFF1h，AFF2h，AFF5h，AFF6h，F3，F4，F7，F8，FCC3h，FCC4h，FCC5h，FCC6h，T7，T8，CCz，CCP3h，CCP4h，CCP6h，Pz，P3，P4，P7，P8，PPO1h，PPO2h，POO1，POO2和Fz三十个通道组成。fNIRS系统的采样率为12.5 Hz。在额叶，运动和视觉区域放置了十四个光源和十六个检测器，形成了36条通道。光电二极管之间的距离为30 mm。EEG电极位置与fNIRS光电二极管位置如图3所示(浅色圆圈为EEG电极位置，浅色方块为NIRS光源位置，深色方块为NIRS探测器位置)。

图3 EEG电极与fNIRS光电二极管位置分布图

数据集包含心理算数MA数据集。数据集将EEG原信号下采样至200 Hz，fNIRS原信号下采样至10 Hz。MA数据集有心算和基线任务，且每个受试者进行60次试验。图4为一次实验的具体流程，包括2 s的视觉介绍，10 s的任务时间段和14 s～16 s的休息时间。在MA任务的过程中，要求受试者从“三位数”中减去一位数字(例如123－9)，并从先前的减法结果中重复减去一位数字，直到任务完成。在MA任务中，通过休息来执行基线任务。

图4 试验任务时间轴

2.2 数据预处理

对EEG信号使用六阶巴特沃斯零相位滤波器进行4 Hz～35 Hz带通滤波，目的是消除干扰和噪声。HbO和HbR的数据首先下采样到10 Hz。fNIRS由多个发射近红外光的光源和接收反射光的检测器组成。为了到达大脑，光线沿着头皮，组织和头骨穿过。在fNIRS系统中，修正的Beer-Lambert定律用于将光强度测量值转换为HbO和HbR的血液动力学变化[25]。将fNIRS信号通过0.01 Hz～0.1 Hz的六阶零相位巴特沃斯滤波器。采用实验前5 s的HbR和HbO浓度数据的均值进行基线校正。文献[24]中，对MA任务实验得出选取7 s～10 s的时间窗数据具有最好的分类结果，因此本文对EEG和fNIRS选取7 s～10 s的时间窗数据。

2.3 整体框架

实验中，采用10×5折交叉验证方法，即将原始数据集按照4∶1划分为训练集和测试集，并重复10次实验，增加分类结果的可靠性。其中通过训练集数据计算通道的PF系数，并设置合理PF权重系数与阈值从而对通道进行选择。权重系数与阈值是通过交叉验证确定的。测试集则使用交叉验证确定的PF权重系数与阈值，对已选择的合理时间窗数据和通道进行特征提取与SLDA分类。整体框架如图5所示。

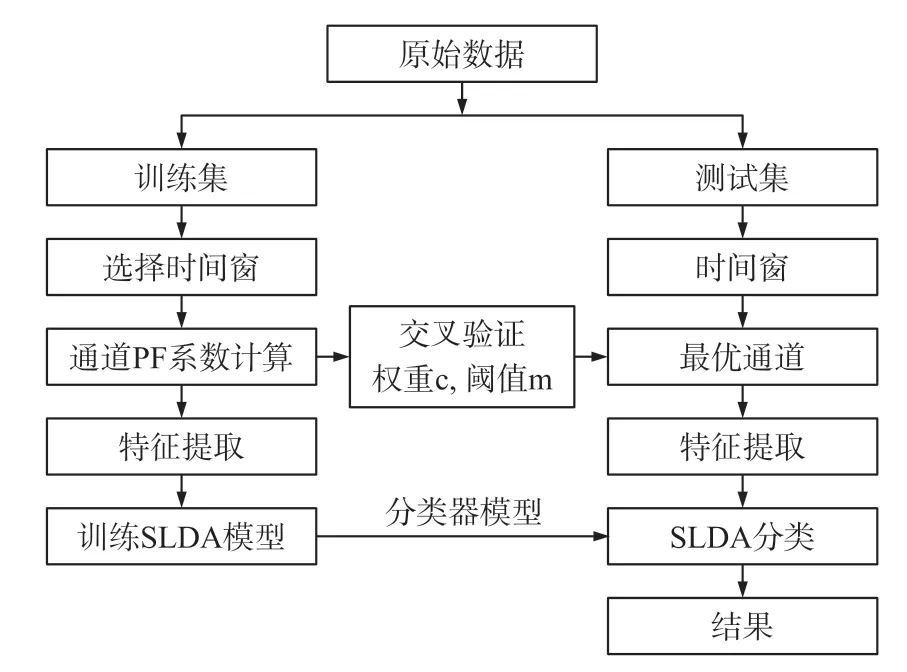
图5 整体框架图

3 结果与讨论

3.1 PF权重系数c和阈值m的设置

根据2.1.2节所述的基于PF系数的通道选择方法，通过改变m与c可以确定EEG、fNIRS和Hybird三种模态下准确率与通道数目的关系。阈值m设置与通道数目设置本质上是一致的，因为当阈值m变大时，意味着通道对应的PF值需要大于m，即通道数目变少。为了更清晰地表明通道选择结果，本文使用通道数目进行分析。如图6所示，其中色度栏为准确率大小，准确率越大，颜色趋于浅色；准确率越小，颜色趋于深色。以受试者2为例，图6(a)、(b)色度图分别表示EEG、fNIRS通道数目与权重c对任务分类精度的影响，根据验证集分类准确率，从而选择最优的权重系数c与阈值m用于后期的测试集，最终对系统性能进行评估。其中，在EEG与fNIRS单模态情况下，通道数目与权重的设置分别为6(neeg)，0.9(ceeg)与24(nfNIRS)，0.9(cfNIRS)时，MA任务的分类准确率最高。图6(c)色度图表示在Hybird情况下，chybird＝0.8，EEG与fNIRS通道数目为9(neeg)和21(nfNIRS)时MA任务的分类准确率最高。图6显示了三种模态下不同参数设置时分类任务准确率波动较大，相比于主观选择权重和阈值这也说明了交叉验证的必要性。

图6 EEG，fNIRS通道数目与权重对任务分类精度的影响

3.2 通道选择的结果

采用基于PF系数的通道选择方法，选择最相关心算任务同时可以提高分类性能的通道。以受试者2为例，根据PF系数值与通道分布的关系可以表示出地形图，如图7所示。其中色度栏为PF值的大小，PF值越大，颜色趋于浅色；PF值越小，颜色趋于深色。PF系数用于表征通道的重要性。图7可以说明EEG与HBO通道分布分别在运动感知区和前额叶皮层区域更为重要；HBR通道分布在运动感知区与前额叶皮层区域更为重要。这与之前的研究相一致[24，26]，也在一定程度上验证了该方法的合理性。

图7 受试者2的PF系数通道分布地形图

3.3 分类性能的比较

本文基于PF系数所选的通道分别提取了EEG，fNIRS和Hybird的三组特征集，并对29个心算任务受试者进行12次分类实验。分类精度为100%表示性能很好可以准确区分心算任务，而50%表示性能较差。图8(a)和(b)分别显示了EEG和fNIRS与Hybird分类精度相比，不同受试者分类精度散点图。圆点代表不同的受试者，横坐标为单模态的分类准确率，纵坐标为多模态的分类准确率。虚线对角线上方的圆圈表示通过Hybird组合分类性能优于EEG/fNIRS的受试者。超过90%和82.8%的受试者分别通过Hybird模态得到了更好的分类准确率。相比EEG和fNIRS分类准确率，Hybird测量的平均性能提高了10.6%和2.4%。实验结果表明，采用基于PF系数进行通道选择的多模态BCI可以十分有效的提高系统性能。

图8 EEG(a)/fNIRS(b)分类精度与Hybird分类精度散点图

本文比较了没有进行通道选择(All Channel)、仅基于Pearson相关系数的通道选择方法、仅基于Fisher值的通道选择方法和基于PF系数的通道选择方法。表1显示了29个受试者在四种方法下，EEG，fNIRS和Hybird这三种模态下的平均MA任务分类准确率。在MA任务中，fNIRS比EEG的有更好的分类性能。四种方法中，对Hybird采用PF方法可以取得最好的分类准确率，达到90.8%。而对Hybird分别采用Pearson方法和Fisher方法的分类准确率为87.3%与88.6%。在四种方法中的不同模态组合下，进一步验证了多模态系统的优势，提升了分类准确率。不仅如此，在四种方法中的不同模态下，采用PF方法均比其他方法有更好的分类性能，表明该方法能够更有效地去除冗余信息，不仅提升了数据相关性，还提升了两类任务特征的可分性，从而选出最佳的通道组合。

表1 不同通道选择方法在不同模态组合下的分类精度表

针对本文所使用的数据集，其他研究者也提出了许多方法，具体结果如表2所示。从表2可知，同样针对心算任务分类，使用多通道张量子空间学习和回归方法[27]得到的EEG准确率为77.0%；在方法[28]中，使用基于希尔伯特变换和导数求和的方法提取fNIRS特征，采用KNN进行分类，得到fNIRS的准确率为84.9%；在方法[24]中，采用CSP提取EEG特征，均值，平均斜率提取fNIRS特征，最后采用SLDA分类，得到Hybird的准确率为88.1%。对比于上述其他方法，本文提出的方法对EEG，fNIRS和Hybird的分类性能均得到了提升。

表2 使用相同数据集的研究比较

4 结论

本文提出了一种基于PF系数的EEG-FNIRS通道选择方法，用于基于心算任务的BCI系统的任务分类。分别计算通道的Pearson相关系数以及特征的Fisher值。由于Pearson相关系数代表了信号之间的相关性，Fisher值代表了两类任务的特征之间可分性。通过调节权重系数c来调整最优通道组合，同时兼顾了信号的相关性以及特征的可分性，减少通道之间的冗余信息。然后用CSP和SLDA对最优的通道组合进行特征提取和分类。对MA数据集的分类实验结果表明PF方法所选出的通道组合能有效的避免个体性差异以及不同通道之间的差异，并且通道分布合理，提高了分类的准确率。值得注意的是，本文算法虽然提升了分类准确率，但进行PF通道选择的过程时间较长，需要在进行特征提取后，根据分类结果确定最优的参数，此过程较为繁琐。在以后的工作中，会考虑提升算法效率从而减少算法时间。