修正摆线钟表齿轮的参数化设计

赵战峰，余尚行，潘朝

（广东轻工职业技术学院，广州 510300）

0 引言

钟表齿轮是修正摆线齿廓齿轮，主要用于仪器仪表、钟表、计时器。钟表齿轮有其不可替代的优点，但是由于刀具规格无法标准化，制造难度大，本文研究整理了一套设计钟表齿轮的方法，为其数控加工打下了基础。

1 摆线齿轮的齿廓曲线及特点

摆线齿轮的齿廓曲线由内、外摆线组成的，齿根部分为内摆线，齿顶部分为外摆线[1]（如图1）。当生成圆直径等于基圆半径时，生成的内摆线为一条径向直线，故齿廓的内摆线也可以是一条直线。基圆是摆线齿轮的节圆，也是其分度圆[2]。

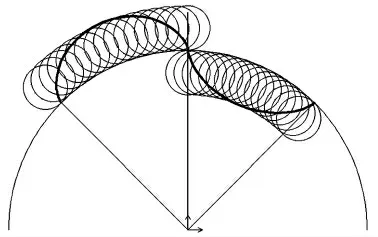
图1 理论摆线

摆线齿轮传动的特点如下：

1）摆线齿轮的模数小，模数可以小至0.1 mm。

2）摆线齿轮的最少齿数可达6齿，单级传动即可实现较大传动比。

3）啮合齿廓为内外摆线凸凹接触，故接触面积大，接触应力小。

4）摆线齿轮啮合线长，磨损小且均匀，润滑良好。5）摆线齿轮啮合时无滑动，传动效率较高。

6）摆线齿轮在节点处正常啮合时，径向分压力极小，即使采用滑动轴承摩擦力也很小，对轴承的磨损作用小。

7）传动中啮合角不恒定，受力不够平稳。

8）摆线齿轮传动节圆必须等于分度圆，不具可分性，否则将导致传动比改变，传动不良。

9）摆线齿轮的齿数、模数相同才可以共用刀具，制造困难。

10）互换性差，模数相等、生成圆半径相等的齿轮才可以互换。

2 修正摆线齿轮的分类及用途

摆线齿轮具有许多优点，在钟表计时机构、时控机构、压力表、油泵、液压马达中应用广泛。流量计、真空泵、风机中用的罗茨齿轮也是一种摆线齿轮。摆线针轮常用于行星齿轮减速机中。

在实际应用中，根据实际情况经常采用修正摆线齿轮，以简化齿形，降低制造难度，满足具体需求[3]。在钟表传动和仪器仪表中普遍采用圆弧直线修正摆线齿轮、双圆弧修正摆线齿轮和摆线销轮[1]。

3 钟表齿轮的特点

1）钟表传动的特点。增速传动（即大齿轮带小齿轮）；单向传动；以尽可能短的传动链获得大传动比；动力储备有限，对能量损耗敏感；为了减小摩擦阻力，支承轴径细小，齿轮传动的径向力要尽可能小[3]。

基于上述特点，钟表齿轮的齿廓曲线常用圆弧直线修正摆线和双圆弧修正摆线。

2）圆弧直线修正摆线齿廓如图2所示，齿根部分是一条径向直线（生成圆直径等于基圆半径的特殊内摆线），齿顶部分是一条近似外摆线的圆弧。加工这种齿轮时，相同模数、不同齿数的齿轮刀具不同，因此所需的刀具规格繁多[1]。圆弧直线修正摆线齿轮传动的特点如下：

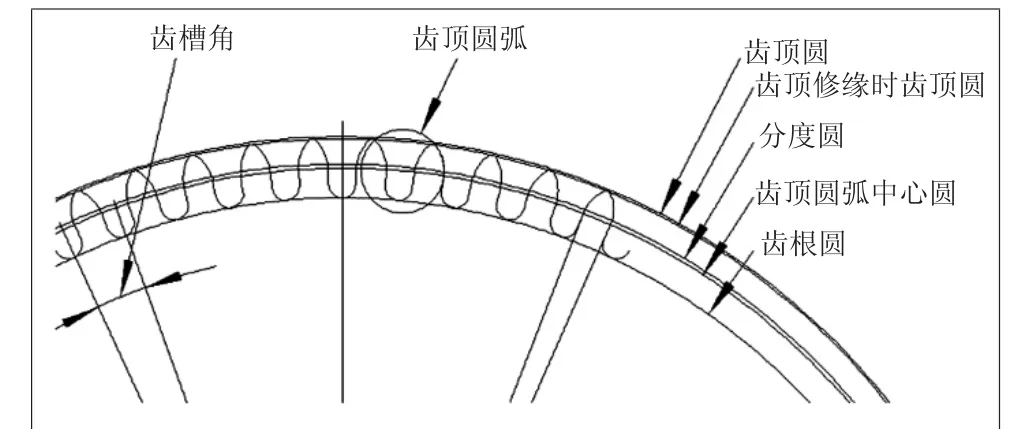
图2 圆弧直线修正摆线齿廓

a.侧隙、顶隙较大，阻力小，传动灵活顺畅；

b.重合度只能为1，即传动中只能一对齿啮合；

c.进啮角小，传动力矩平稳，传动效率高；

d.瞬时传动比不为常数。

3）双圆弧修正摆线齿廓是由2个半径相等的圆弧近似地代替摆线齿轮齿顶和齿根的内外摆线。加工这种齿轮时，对相同圆弧半径、相同模数、不同齿数的齿轮刀具选择相同，所需的刀具规格少。

4 圆弧直线修正摆线钟表齿轮几何尺寸计算

其几何尺寸计算公式列于表1，计算中的系数如表2～表8[1]所示，各部分尺寸的意义如图3所示。

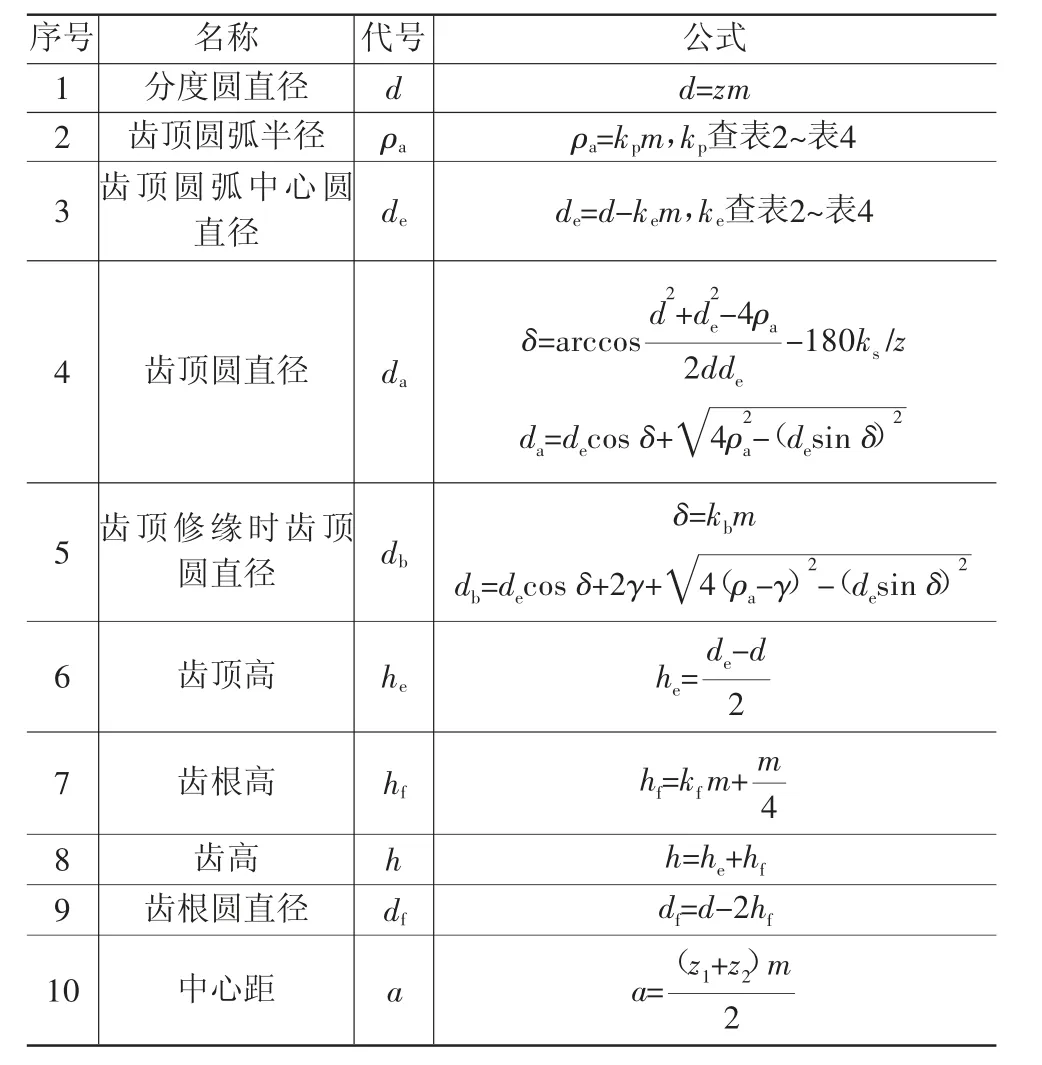
表1 钟表齿轮的几何尺寸计算公式

表2 升速传动时小齿轮的系数ke、kp

表8 齿厚系数ks

小齿轮模数第一系列：0.1、0.12、0.14、0.2、0.25、0.3、0.4、0.5、0.6、0.8、1。

5 钟表齿轮参数化设计

在Creo中创建钟表齿轮的参数化模型，方法如下。

1）以齿顶修缘时齿顶圆直径创建圆柱体，作为齿轮坯料。

2）绘制图4所示截面，拉伸切出一个齿槽。

3）按齿数阵列齿槽。

4）设置表9所示参数。

5）定义表10所示关系式。将表10的关系式变量赋值给相应的尺寸。

此全参数化模型，修改参数（例如：齿数、模数、计算系数等），关系式重新计算时，模型立即改变。为设计带来极大的便利，所得的模型可以直接用于数控编程。

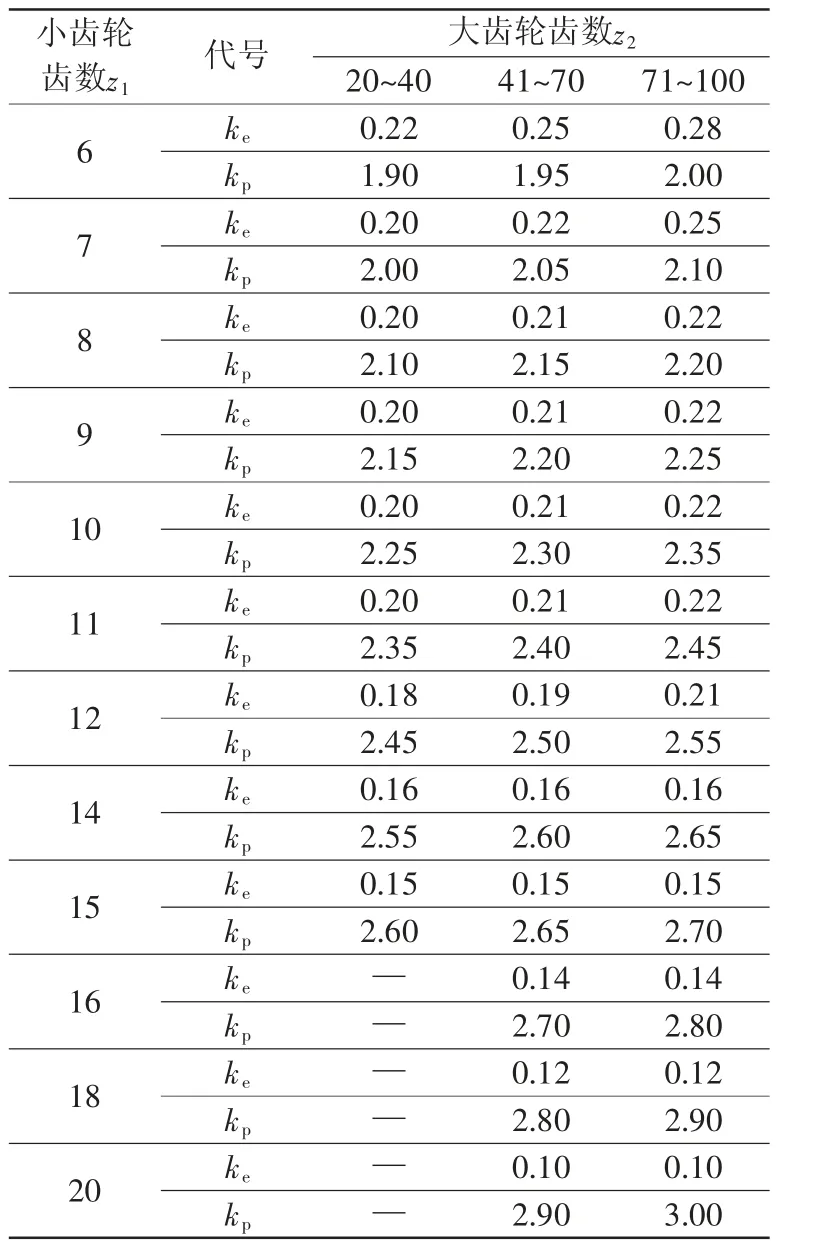
表3 升速传动时大齿轮的系数ke、kp

6 结论

用以上方法创建的Creo参数化模型，可以方便地创建不同模数、不同齿数的钟表齿轮三维模型，可以直接用于数控铣床、电火花线切割机床、激光加工机床等设备的数控编程及加工。使钟表片齿轮的加工效率大大提高，不再受制于规格繁多的钟表齿轮滚刀和成型刀。

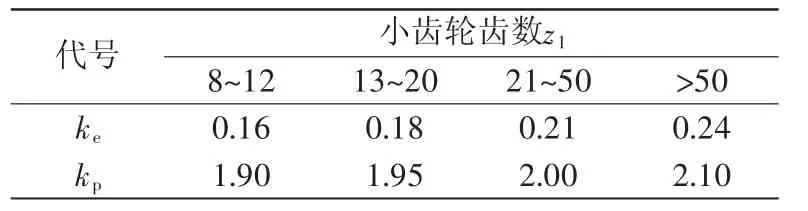
表4 升速或减速传动时钟表齿轮的系数ke、kp

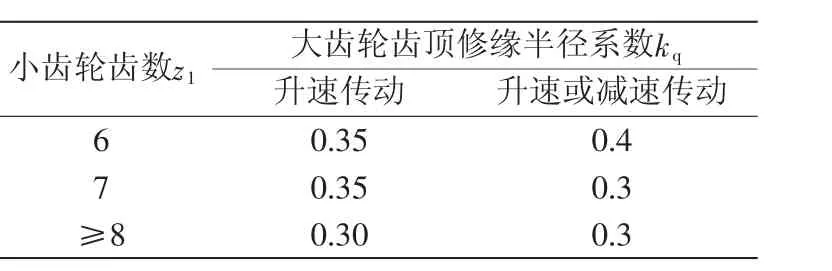
表5 大齿轮齿顶修缘半径系数kd（注：小齿轮齿顶一半不修缘）

表6 齿轮齿根高系数kf

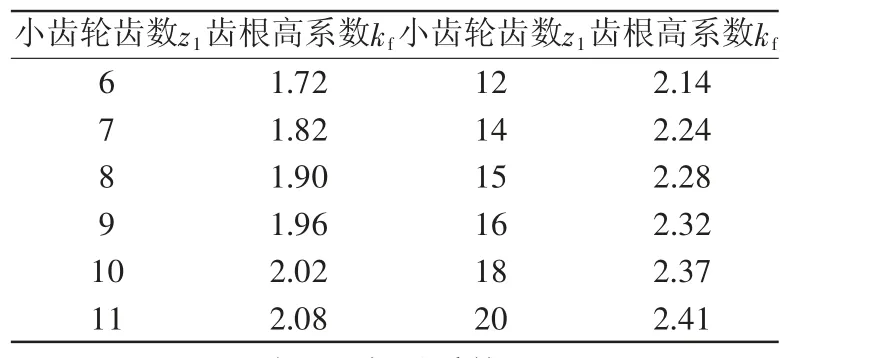
表7 升速传动时小齿轮齿根高系数kf

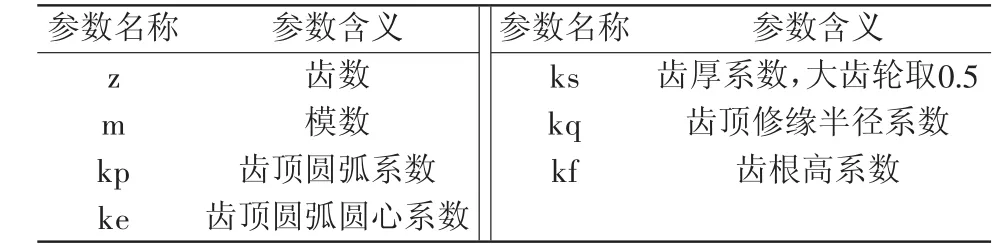
表9 Creo模型参数

表10 Creo关系式

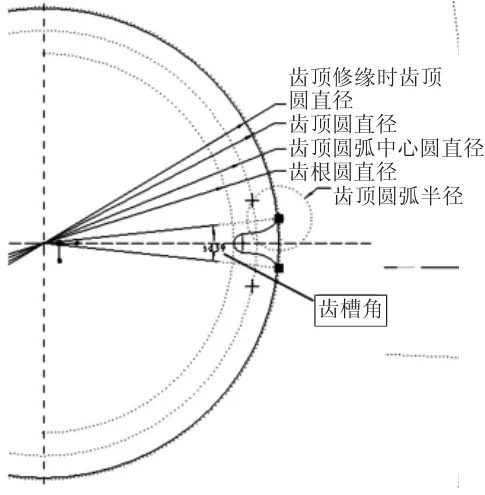
图3 各部分尺寸的意义

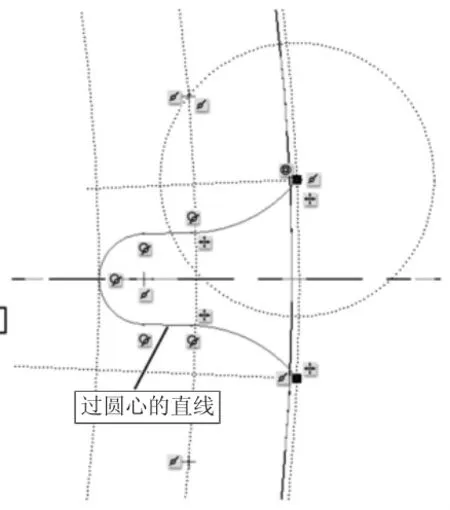
图4 Creo绘制的钟表齿轮齿槽