LRB基础隔震结构在极罕遇地震作用下的碰撞响应研究

许立英，林友勤，吴应雄，胡广杰，苏福庆，章永伟

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621010;2.福州大学 土木工程学院，福建 福州 350108；3.华中科技大学 土木与水利工程学院，湖北 武汉 430074;4.福建梓诺建筑工程有限公司，福建 厦门 361000;5.龙岩市西安建筑工程有限公司，福建 龙岩 364000)

目前基础隔震技术被广泛应用于医院、火车站等建筑。而大量的震害研究表明，建筑结构在地震中发生碰撞是建筑物破坏甚至倒塌的重要原因之一。国内外学者对建筑结构碰撞问题展开研究。TSAI[1]发现碰撞会导致弹性剪切梁产生极高的加速度响应，非线弹性的碰撞模型可以减小加速度响应。Matsagar等[2]发现碰撞会导致上部结构加速度增加，但发生碰撞的隔震结构仍然比非隔震结构的抗震性能好。Muthukumar等[3]发现不同模型的位移响应很接近，地震动峰值加速度越大，碰撞过程中的能量损失越大。沈麒等[4]基于弹性和黏弹性碰撞模型，提出了弹塑性碰撞模型，并给出了等效碰撞周期和等效碰撞阻尼的计算公式。朱宏平，叶昆等[5]发现降低设防烈度设计隔震后的上部结构不利于建筑抵抗极罕遇地震，使用大直径和低橡胶剪切模量的铅芯橡胶隔震支座有利于提高结构的抗震性能。彭刚辉等[6]发现碰撞刚度、恢复系数和间隙大小对隔震桥梁结构在地震作用下发生碰撞时的峰值碰撞力、墩顶峰值位移以及隔震支座最大水平剪力均有较大影响。

按照目前我国规范要求设置隔离缝可以保证隔震层在罕遇地震下的变形需求，但我国实际发生的大地震的震中烈度比当地的设防烈度大得多，这就意味着可能发生比罕遇地震更为强烈的地震动。

并且在最新的《中国地震动参数区划图》[7](GB 18036—2015)在传统“三级地震作用”基础上增加了极罕遇地震作用，修改为“四级地震作用”。在极罕遇地震作用下基础隔震结构是否会出现隔震层水平变形超过隔震缝宽度而与周围挡土墙碰撞的情况等均需要进一步研究。

吴应雄等[8]发现远场长周期地震动下的隔震结构的放大效应较普通地震动下的明显，并对隔震层位移反应的影响较大。陈启冬等[9]研究发现隔震结构在硬土地基上能发挥较好的减震效果，而软土地基上减震效果明显减弱，其抗震设计应重点关注。王林建等[10]发现长周期作用下基础隔震结构减震效果比普通地震动差;大底盘楼层的减震效果在长周期地震动下，较塔楼明显降低。吴应雄等[11]通过国内现有的隔震建筑构造相关设计成果及存在问题的阐述，讨论了我国隔震构造技术研究的下一步发展方向。

本文的研究内容主要涉及以下三个方面：

(1)介绍建筑结构碰撞研究常用的碰撞分析方法以及各种碰撞模型的特点，并选用改进的Kelvin模型进行本文的研究。将上部结构简化为单自由度非线性体系，建立LRB基础隔震结构的碰撞分析模型以及LRB基础隔震结构发生碰撞时的运动方程。

(2)采用叠加小波函数的方法对选取的22条地震动记录进行调整，使调整后的地震动平均加速度反应谱与极罕遇地震加速度反应谱相拟合。用MATLAB进行非线性时程分析。基于非线性时程分析的结果，比较碰撞和不碰撞两种情况下，基础隔震结构在极罕遇地震作用下的动力响应，研究隔震层与周围挡土墙的碰撞对基础隔震结构动力响应的影响。

(3)比较不同碰撞参数下，基础隔震结构在极罕遇地震作用下的碰撞响应随隔震系统力学性能参数和上部结构屈服承载力的变化曲线，分析隔震系统力学性能参数、上部结构屈服承载力以及碰撞模型参数对LRB基础隔震结构在极罕遇地震作用下的碰撞响应的影响。

1 基础隔震结构碰撞的基本理论及方法

1.1 改进的Kelvin模型

Jankowski[12]将碰撞过程分为碰撞开始阶段和碰撞恢复阶段，发现碰撞过程中的能量损失主要发生在碰撞开始到碰撞力达到峰值的阶段，碰撞力达到峰值后的碰撞恢复阶段的能量损失很小。Kelvin模型在碰撞过程的两个阶段能量损失相等，而且在碰撞恢复过程中会产生负拉力，与实际情况不符。为了弥补Kelvin模型的不足，叶昆等[13]提出了改进的Kelvin模型，并验证了该模型对建筑结构碰撞研究的适用性。改进的Kelvin模型的碰撞力表达式如下：

(1)

c=ξδ

(2)

式中：ξ为阻尼常数，与回弹系数e有关，表达式如下：

(3)

非线性弹性分析模型的弹簧刚度与碰撞物体的材料属性和形状相关，在实际研究中很难确定，而Kelvin模型的弹簧刚度可以根据碰撞结构的轴向刚度简单而且合理的确定，在结构碰撞研究中的应用更为广泛。Mahmoud等[14]对不同的接触单元模型进行了比较分析，发现不同模型的计算结果相差不大，但激烈碰撞时非线性模型的偏差更大。樊剑等[15]用不同碰撞分析模型研究摩擦型隔震结构的碰撞响应时，发现基于接触单元法的不同碰撞模型间的计算结果相差不大，但线性碰撞模型的计算时间比非线性碰撞模型的要短。因此，本文将采用改进的Kelvin模型模拟碰撞过程，研究基础隔震结构在极罕遇地震作用下与周围挡土墙的碰撞响应。

1.2 基础隔震结构碰撞的分析模型

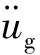
图1 LRB基础隔震结构与周围挡土墙碰撞的分析模型

(4)

(5)

式中:FI、FS分别为隔震层和上部结构的恢复力;FP为隔震层与周围挡土墙碰撞的产生碰撞力。

考虑到基础隔震结构的上部结构在极罕遇地震作用下可能发生弹塑性变形，上部结构的恢复力模型采用双线性模型，隔震层的恢复力模型也采用双线性模型，如图2所示。其中kE、kI分别为LRB隔震支座的屈服前和屈服后刚度；uYD、uYS分别为LRB隔震支座和上部结构的屈服位移；QD、FY分别为LRB隔震支座和上部结构的屈服剪力；kS为上部结构的刚度；α为硬化系数。隔震层和上部结构的恢复力表达式如下所示：

图2 LRB隔震支座和上部结构的恢复力模型

FI=kIuI+QD·zI(uI)

(6)

FS=αkSuS+(1-α)FY·zS(uS)

(7)

式中:zI(uI)、zS(uS)分别为隔震层和上部结构的屈服函数。

基础隔震结构与周围挡土墙的碰撞采用改进的Kelvin模型进行模拟，由改进的Kelvin模型的碰撞力公式，隔震层碰撞产生的碰撞力表达式如下：

(8)

式中，阻尼系数c的表达式如下：

(9)

式中:k为碰撞刚度，e为回弹系数。

为了反映LRB基础隔震结构的动力特性，定义以下参数：上部结构和整个LRB基础隔震结构的自振圆频率，表达式如下：

(10)

上部结构和整个LRB基础隔震结构的阻尼比，表达式如下：

(11)

上部结构和整个LRB基础隔震结构的屈服强度比，表达式如下：

(12)

上部结构和整个LRB基础隔震结构的质量比，表达式如下：

(13)

以及碰撞力和整个LRB基础隔震结构重量的比值，表达式如下：

(14)

将参数代入基础隔震结构碰撞的运动方程，得到：

(15)

(16)

2 碰撞对基础隔震结构动力响应的影响

2.1 加速度反应谱及地震动的选择与调整

假设所在地区的设防烈度为8度，设计基本加速度0.3g，II类场地，设计地震分组为第二组，《中国地震动参数区划图》[7](GB 18036—2015)规定的极罕遇地震的峰值加速度αmax=0.870g，特征周期Tg=0.45 s，放大系数反应谱平台值场地βm=2.5。基于场地地震动的表征参数，《建筑抗震设计规范》[16](GB 50011—2010)确定的第一拐点周期T0和周期范围上限值Tm分别为0.1 s和6.0 s，下降速度控制系数γ为0.9。依据规范确定的相关参数，极罕遇地震作用的加速度反应谱见图3。

选用ACT-63推荐的22条地震动研究基础隔震结构在极罕遇地震作用下的动力响应，详细的地震动信息如表1所示。为了进行时程分析，需要对选取的地震动进行调整，使调整后的地震动平均加速度反应谱与极罕遇地震加速度反应谱相拟合。本文采用SeismoMatch软件通过叠加小波函数的方法调整选用的22条地震动，调整后的地震动平均加速度反应谱与极罕遇地震加速度反应谱拟合情况如图3所示，从图3中可以看出，调整后的平均加速度反应谱与极罕遇地震加速度反应谱基本重合。

表1 地震动基本信息

图3 调整后反应谱与极罕遇地震作用反应谱的拟合情况

2.2 LRB基础隔震结构动力响应的参数研究

2.2.1 上部结构屈强比对基础隔震结构动力响应影响

本文研究假定结构的超强系数ΩS=2.5，通过计算可以得到基底固定的上部结构的屈服强度比qS,Fix=0.417。现行的建筑抗震设计规范规定，根据计算出的水平方向减震系数，可以在设防烈度的基础上降半度、一度或者一度半对隔震后的上部结构进行抗震设计，这种方法使得上部结构的屈服承载力下降。为了研究上部结构屈服强度比对基础隔震结构碰撞响应的影响，定义上部结构屈服折减系数R，表达式如下：

(17)

R=1.0、1.5、2.0和3.0分别表示按照设防烈度、降半度、降一度和降一度半对隔震后的上部结构进行抗震设计。

隔震周期TI=3.464 s和隔震层的屈服强度比qD=0.06保持不变，通过改变上部结构屈服折减系数R改变上部结构的屈服强度比qS。图4比较了考虑碰撞和不考虑碰撞两种情况下上部结构平均延性系数μm随上部结构屈服折减系数R的变化曲线。图5给出了考虑碰撞和不考虑碰撞两种情况下隔震体系平均最大剪应变γm随上部结构屈服折减系数R的变化曲线，表2比较了在考虑碰撞作用和不考虑碰撞两种情况下，基础固定结构和按照不同设防烈度设计的基础隔震结构在极罕遇地震作用下上部结构平均延性系数的值。

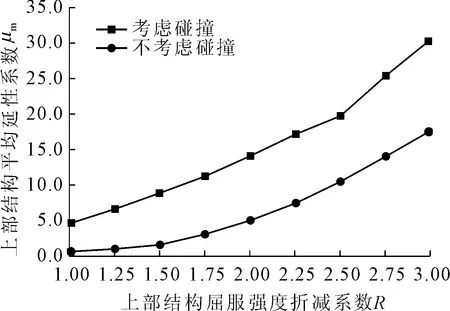
图4 上部结构平均延性系数变化曲线

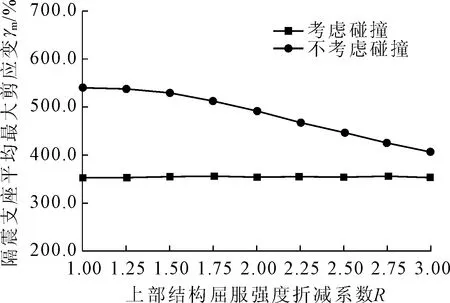
图5 隔震支座平均最大剪应变变化曲线

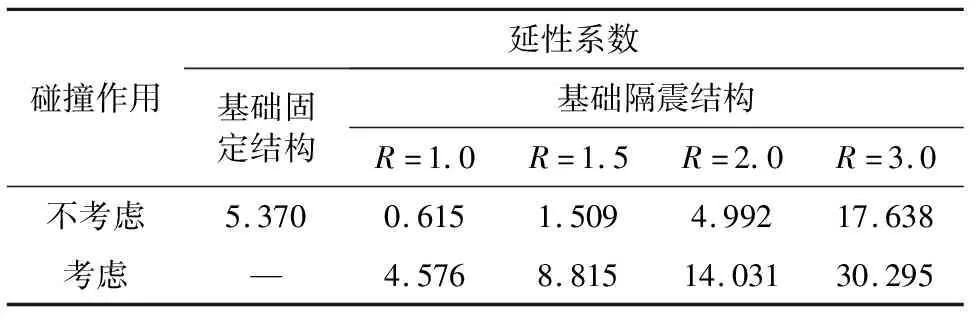
表2 上部结构平均延性系数

综合图4、图5、表2可以得出：

(1)不考虑隔震层在极罕遇地震作用下与周围挡土墙碰撞时，不降设防烈度设计的上部结构的平均延性系数远小于基础固定结构的，降一度设计的上部结构与基础固定结构的平均延性系数差不多；考虑碰撞时，在极罕遇地震作用下按照设防烈度设计的上部结构与基础固定结构的平均延性系数差不多。说明按照设防烈度设计的基础隔震结构不发生碰撞时仍然有很好的抵抗极罕遇地震作用的能力，发生碰撞时的抗震性能降低，但仍然比基础固定结构的抗震性能要好。

(2)不考虑隔震层的碰撞时，在极罕遇地震作用下按照设防烈度设计的上部结构的平均延性系数接近1，上部结构即将出现弹塑性变形；考虑隔震层的碰撞时，在极罕遇地震作用下按照设防烈度设计的上部结构平均延性系数远超过1，上部结构已经出现了弹塑性变形，说明基础隔震结构的上部结构在极罕遇地震作用下很难保持弹性状态。这种现象是因为极罕遇地震的能量很高，而隔震体系的耗能能力有限，上部结构需要通过弹塑性变形耗散地震能量。而且碰撞作用限制了隔震层的水平变形，降低了隔震层消耗地震能量的能力，隔震体系发生碰撞后上部结构需要通过弹塑性变形耗散更多的地震能量，从而产生的弹塑性变形更大。

(3)考虑碰撞和不考虑碰撞两种情况下，随着上部结构屈服强度折减系数增加，上部结构结构屈服承载力降低，上部结构平均延性系数都会加速增大。不考虑碰撞作用时，降一度设计的上部结构在极罕遇地震作用下的平均延性系数大约是极限倒塌状态的一半，降一度半设计的上部结构在极罕遇地震作用下的平均延性系数已经远超过极限倒塌状态的平均延性系数；考虑碰撞作用时，降半度设计的上部结构在极罕遇地震作用下的平均延性系数已经接近极限倒塌状态的平均延性系数。降低上部结构屈服承载力对上部结构动力响应的影响很大，降低设防烈度设计的上部结构在极罕遇地震作用下很有可能会发生倒塌，因此，采用降低设防烈度设计隔震后的上部结构的方法不可取。

2.2.2 隔震体系屈强比对基础隔震结构动力响应影响

隔震周期TI=3.464 s保持不变，隔震体系的屈服强度比qD在0.01～0.15范围内变化。图6给出了考虑碰撞和不考虑碰撞两种情况下上部结构平均延性系数μm随隔震体系的屈服强度比qD的变化曲线。图7给出了考虑碰撞和不考虑碰撞两种情况下隔震体系平均最大剪应变γm随隔震体系的屈服强度比qD的变化曲线。

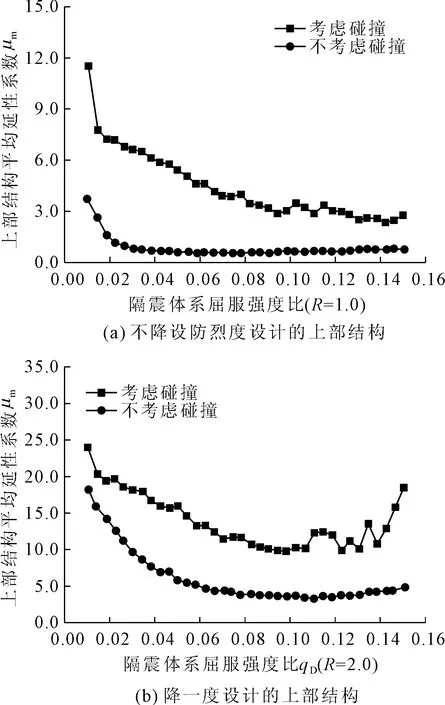
图6 上部结构平均延性系数随隔震体系屈服强度比的变化曲线

图7 隔震支座平均最大剪应变随隔震体系屈服强度比的变化曲线

结合图6、图7可以看出：

(1)不考虑隔震层和周围挡土墙的碰撞时，上部结构平均延性系数随着隔震体系屈服强度比的增大呈现先减小后增大的趋势，说明存在临界的隔震体系屈服强度比使上部结构平均延性系数最小。隔震体系屈服强度比的临界值与上部结构屈服强度比有关，当隔震体系屈服强度比超过临界值时，上部结构平均延性系数在极罕遇地震作用下增加的幅度很小；考虑碰撞作用时，随着隔震体系屈服强度比的增大，上部结构平均延性系数整体呈现减小的趋势，但变化的速度减慢。因此，增大隔震体系的屈服承载力，既可以降低隔震结构发生碰撞时上部结构的动力响应，又可以保证隔震结构不发生碰撞时的抗震性能。

(2)不降设防烈度设计的上部结构在极罕遇地震作用下平均延性系数明显小于降一度设计的上部结构。不考虑碰撞作用时，上部结构平均延性系数最小值都小于极限倒塌状态的平均延性系数；考虑碰撞作用时，不降设防烈度设计的上部结构平均延性系数最小值不到限倒塌状态平均延性系数的1/3，而降一度设计的上部结构平均延性系数最小值接近极限倒塌状态的平均延性系数。降一度设计的隔震结构不考虑碰撞时上部结构的平均延性系数高于按照设防烈度设计的隔震结构碰撞时上部结构的平均延性系数。说明极罕遇地震作用下，降低设防烈度对上部结构动力响应的影响超过了碰撞的影响。

3 碰撞参数对LRB基础隔震结构碰撞响应的影响

3.1 恢复系数对碰撞响应的影响

恢复系数是碰撞分析模型的重要参数，表示碰撞过程中的能量损失，研究表明钢筋混凝土结构碰撞时恢复系数一般在0.4～0.7范围内变化。为了研究恢复系数对LRB基础隔震结构在极罕遇地震作用下碰撞响应的影响，碰撞刚度2.25×109N/m，隔离缝宽度3.5TR保持不变，恢复系数在0.4～0.7范围内变化。图8、图9分别给出了不同恢复系数下，上部结构平均延性系数和平均最大碰撞力随隔震结构力学性能参数(上部结构屈服折减系数、隔震体系屈服强度比和隔震周期)的变化曲线。

图8给出上部结构平均延性系数随隔震结构力学性能参数的变化曲线。从图8中可以看出，不同恢复系数下，上部结构平均延性系数随上部结构屈服折减系数、隔震体系屈服强度比和隔震周期的变化曲线基本重合，说明恢复系数对LRB基础隔震结构上部结构在极罕遇地震作用下的碰撞响应影响不大。

图8 上部结构平均延性系数随隔震结构力学性能参数的变化曲线(不同恢复系数)

图9给出了不同恢复系数下，平均最大碰撞力随隔震结构力学性能参数(上部结构屈服折减系数、隔震体系屈服强度比和隔震周期)的变化曲线。可以看出，不同恢复系数下，平均最大碰撞力随上部结构屈服折减系数、隔震体系屈服强度比和隔震周期的变化曲线之间有差异但差别不大，说明增大恢复系数可以降低LRB基础隔震结构碰撞时的碰撞力峰值，但影响的程度有限。

图9 平均最大碰撞力随隔震结构力学性能参数的变化曲线(不同恢复系数)

3.2 碰撞刚度对碰撞响应的影响

采用线性碰撞模型研究建筑结构碰撞响应时碰撞刚度的取值范围一般为1.0×109N/m～1.0×1010N/m,为了研究碰撞刚度对LRB基础隔震结构碰撞响应的影响，恢复系数取0.5，隔离缝宽度取3.5TR。图10、图11分别给出了不同碰撞刚度下，上部结构平均延性系数和平均最大碰撞力随上部结构屈服折减系数、隔震体系屈服强度比和隔震周期的变化曲线。

图10 上部结构平均延性系数随隔震结构力学性能参数的变化曲线(不同碰撞刚度)

图11 平均最大碰撞力随隔震结构力学性能参数的变化曲线(不同碰撞刚度)

可看出：碰撞刚度为1.00×109N/m和2.25×109N/m时，平均最大碰撞力随隔震结构力学性能参数的变化曲线比较平滑，上部结构平均延性系数随隔震结构力学性能参数的变化曲线也比较平滑。碰撞刚度为5.00×109N/m时，平均最大碰撞力和上部结构平均延性系数随上部结构屈服折减系数和隔震周期的变化曲线比较平稳，随隔震体系屈服强度比的变化曲线波动较大。碰撞刚度为1.00×1010N/m时，平均最大碰撞力和上部结构平均延性系数随上部结构屈服折减系数和隔震周期的变化曲线波动较小，随隔震体系屈服强度比的变化曲线波动较大。不同碰撞刚度下，上部结构平均延性系数随隔震体系力学性能参数的变化曲线基本重合。不同碰撞刚度下，平均碰撞力随隔震结构力学性能参数变化曲线差别较大，碰撞刚度对平均碰撞力的影响较大，减小碰撞刚度可以降低碰撞力峰值。

4 结 论

(1)LRB基础隔震结构在极罕遇地震作用下隔震支座水平变形极有可能会超过隔震缝的宽度，甚至会超过极限破坏状态的变形，隔震层与周围挡土墙的碰撞有效限制了隔震支座的水平变形。根据隔震支座的极限剪应变设置适当隔震缝的宽度，可以保障隔震支座在极罕遇地震下的安全。

(2)按照设防烈度设计的基础隔震结构在极罕遇地震作用下的抗震性能仍然优于基础固定结构，而降低设防烈度设计的基础隔震结构抵抗极罕遇地震的能力不足，在极罕遇地震作用下可能会倒塌，因此降低设防烈度设计隔震后的上部结构的方法不可取。

(3)基础隔震结构在极罕遇地震作用下与周围挡土墙的碰撞能有效限制隔震支座的水平变形，但会显著加剧上部结构的动力响应，使上部结构进入弹塑性变形阶段。在保障隔震支座安全的情况下，应尽量降低基础隔震结构发生碰撞的概率。

(4)不同碰撞参数下，上部结构平均延性系数随上部结构屈服折减系数、隔震体系力学性能参数的变化曲线基本重合，上部结构碰撞响应对碰撞模型参数的变化不敏感。但碰撞刚度较大，而隔震体系屈服强度很小时，上部结构平均延性系数随隔震体系屈服强度比增加有较大波动。

(5)提高上部结构或隔震体系的屈服承载力可以降低上部结构的碰撞响应，上部结构碰撞响应对隔震周期的变化不敏感。