重载铁路货车车轮踏面磨耗表征方法及其规律分析*

杜 彬，胡军海，宋冬利

（1 国家能源投资集团有限责任公司，北京100120；2 西南交通大学 牵引动力国家重点实验室，成都610031）

我国重载铁路的需求在不断地增长，调整运输结构、增加铁路运输量的决策部署，进一步提升运输能力，降低物流成本，优化产品供给。随着大载重高负荷运行的铁路货车越来越成为常态，货车车轮的磨耗情况必定较之前严重，研究发现车轮磨耗受左右车轮轮径差的影响较大［1-2］。基于此，研究轮径差对重载铁路货车轮对的磨耗显得至关重要［3］，相关研究人员充分利用现有的科学技术手段，并从数据和理论的角度大量研究轮径差对轨道车辆车轮的磨耗影响过程［4-5］。文中从多个角度分析重载铁路货车车轮磨耗的影响，结合数据对磨耗的影响，得到不同情况下踏面磨耗量和磨耗位置的变化规律。以往针对踏面磨耗的研究主要集中于名义滚动圆处磨耗量的分析，而很少关注对车轮磨耗位置的分析［1-7］。

1 车轮踏面全廓形磨耗测试

在开行58 辆编组的某型铁路货车试验列车中，试验列车选取的扣车标准为段修后12 个月的正常营运列车，并投入大量工作人员对列车各部分进行分解检测，其中按照要求对整列58 辆车的所有车轮廓形进行检测并记录相关数据。铁路货车车轮廓形为中华人民共和国铁道行业标准的LM 廓形，标准踏面轮缘高为固定值，因此实际工程中磨耗量主要是检测名义滚动圆处至轮缘最高处垂直距离与标准LM 踏面廓形轮缘高的差值。通过这种方法检测出的磨耗只能是踏面上名义滚动圆位置的磨耗，无法描述整个踏面磨耗情况，建立一种能够计算和评价整个廓形磨耗情况的数学模型显得尤为重要。

1.1 全廓形匹配分析基础

铁路货车检修公司在列车段修期结束后对其进行一次段修，段修中将对超限车轮进行旋修或更换新轮，未超限车轮则予以放行，不扣押旋修或更换新轮，段修结束后不记录旋修后车轮标准，因此很难追踪上一个段修后支出车轮对应的标准踏面，给全廓形磨耗分析带来一定困难。调研铁路货车检修公司实际旋修标准，对某一实测廓形数据进行匹配分析，寻找上一次段修期旋修后的标准踏面廓形，匹配分析流程如图1 所示，经过匹配分析后得到最接近于甚至找出上次段修后的标准LM 踏面；最终分析结果如图2 所示。

图1 车轮踏面廓形磨耗计算

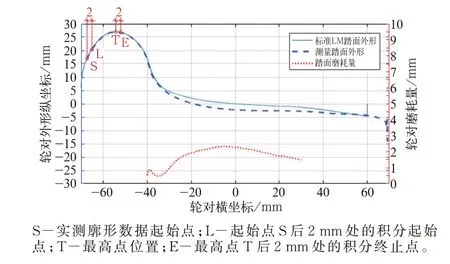
图2 车轮踏面廓形磨耗计算

通过大量调研发现，以图2 所示轮缘最高点对轮缘分左右侧，货车轮对的轮缘左侧（轮对内侧）区域处于不接触磨耗的状态且车轮轮缘右侧靠近最高点部分区域几乎不发生接触磨耗，能保持磨耗后车轮轮缘的大部分区域廓形与上次段修后的标准车轮一致。

1.2 全廓形匹配分析原理及磨耗计算

首先确定实测廓形（A）与标准廓形（B）轮缘最高点，将其廓形数据分别储存在A、B中，轮缘最高点位置TA、TB为式（1）：

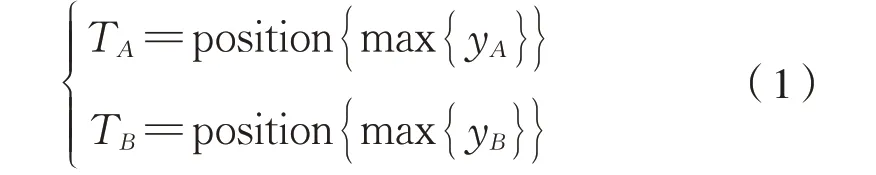
确定轮缘最高点后计算最高点的横纵坐标差Δx和Δy，将 实 测 廓 形 沿x、y方 向 分 别 移 动Δx和Δy距离，得到实测廓形轮缘最高点与标准廓形轮缘最高点重合后的实测廓形数据A1；廓形曲线SLTE 即为上文提到轮缘不接触磨耗部分，列车运行中该部分廓形可确定原则上不发生变化，作为匹配标准廓形依据，并作如下匹配分析：

实践中发现，实测廓形数据中T点的确会受人工测量质量的影响，继而影响匹配标准廓形的准确性，需要将最高点重合后对实测廓形上下左右微调来减少这种测量误差，并对实测廓形与标准廓形所围成区域从L至E面积积分，其面积积分为式（2），最小面积积分为式（3）：

式中：SDij为上下横移第i次且左右横移第j次的面积积分；Dm为轮缘厚m的标准廓形与实测廓形的最小积分面积，根据车轮旋修标准更换不同轮缘厚m再次计算分析得到新的Dm。

由以下表达式匹配得到实测廓形对应的标准车轮廓形，轮缘厚为m，分析区域围成面积为D，围成面积的最小值dm，并计算踏面位置k处磨耗量Wk，分别为式（4）、式（5）：

图2 所示为标准LM 踏面与实测踏面匹配并计算轮对坐标系横坐标［-40，30］区间内的磨耗情况。

根据以上分析方法计算某实测轮对左右轮廓形磨耗如图3 所示，其中左侧车轮轮径值为823 mm，右侧车轮轮径值为820 mm。分析发现同一条轮对存在轮径差的时候，有如下的情况：轮径大的一侧踏面磨耗量相比轮径小的一侧踏面磨耗量少；轮径大的车轮踏面磨耗区域朝着远离轮缘方向，轮径小的车轮踏面磨耗区域朝着靠近轮缘方向。

图3 车轮廓形磨耗特征值确定

2 车轮踏面全廓形磨耗的量化指标

实测轮对匹配后的全廓形分析每次只针对单条轮对，实际情况需要对整列车的大量轮对数据分析处理，找出轮对磨耗的普遍规律。根据实测廓形匹配标准廓形并分析计算磨耗，在此基础上对分析的磨耗量提取特征值，以便对大量磨耗数据批量分析，而不仅局限于每次最多只分析一条轮对，最大化利用数据的同时避免偶然现象影响磨耗规律的分析，提高磨耗规律分析结果的可靠性和通用性。

如图3 所示对廓形磨耗数据进行指标化，确定磨耗量最大值点P的磨耗量及其所在位置，以P点磨耗量值的R（0.5＜R＜1）倍作为一个磨耗基准点寻找左右分位点RL和RR的磨耗位置。其中R作为一个待确定的分位系数，左右分位点为式（6）：

式中：xP、xL、xR分别为车轮磨耗最大值、左分位点RL、右分位点RR的横向位置。其中靠近轮缘的左分位点最为关键，其位置可分析偏磨现象，效果主要取决于R值的确定，通过不同的分位系数R值分析相关规律并确定效果最佳R值。

2.1 踏面全廓形磨耗量分析

工程检修中磨耗量测量以踏面名义滚动圆位置的磨耗情况作为车轮磨耗的表征值，实际车轮磨耗最大值绝大部分集中于名义滚动圆靠轮缘一侧（轮对内侧），因此单纯地以名义滚动圆处磨耗值表征车轮磨耗情况过于片面且效果不算很理想。在获得廓形磨耗的基础上，车轮磨耗量指标将用最大磨耗量来表征，并且最大磨耗量的位置不固定。车轮磨耗量最大值的分布情况如图4 所示。图中轮径差表示在同一轮对中当前车轮直径与另一车轮直径之差，轮径差为正数代表当前车轮在轮对中为大轮径，反之则为小轮径。

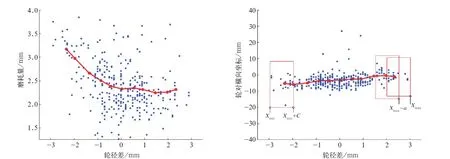
图4 车轮磨耗量最大值的分布情况

图4 中蓝色点为车轮磨耗最大值及其在车轮中的位置分布情况，图4 中右图明显看出磨耗最大值点几乎都处于轮对内侧。为直观地看出磨耗的变化规律，对磨耗点的磨耗值及其对应的轮径差和相对车轮坐标系的位置分段求平均值，并将各 点连线分析如图4 所示，计算公式为式（7）、式（8）：

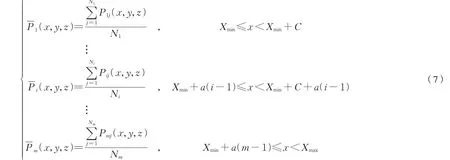
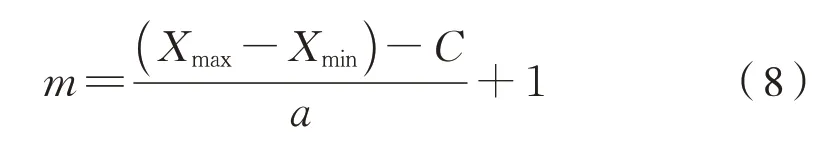
式中：Pij（x，y，z）表示磨耗最大值点P在第i个分段区间内的第j个数，x，y，z分别表示P点对应的轮径差、车轮横坐标和磨耗量；Ni和C分别表示第i个分段区间内的P点数量和区间长度；［Xmin，Xmax］是所有分析数据所在的区间；a为区间移动的步长，且Xmin+a（m-1）=Xmax-C；m为分段求平均的区间移动次数。

为保证最大化地利用数据，通常选择区间移动的步长a小于分段区间长度C，在分段求平均值时相邻区间段有重叠部分，其中a值越小重叠部分越多，数据利用越充分。实践发现数据集中在小轮径差附近，因此a值需要合理选择以避免在轮径差大且数据稀疏的情况下引起分析误差。

2.2 踏面全廓形磨耗位置分析

以上确定磨耗最大值点的任一车轮，根据式（6）分别计算左右分位点，暂取分位系数R=0.9，同理根据式（7）和式（8）对大量磨耗数据分段求平均值，得到磨耗分布图，如图5 所示。图中变化曲线表示磨耗随轮径差在车轮踏面坐标系上的位置变化。

图5 中左分位点曲线靠近轮缘，曲线变化趋势能很好地反应轮缘磨耗趋势，当曲线变化朝车轮坐标系负方向发展时表示磨耗位置朝轮缘磨耗发展，同时左右分位曲线之间的距离能很好地描述磨耗宽度的变化趋势。

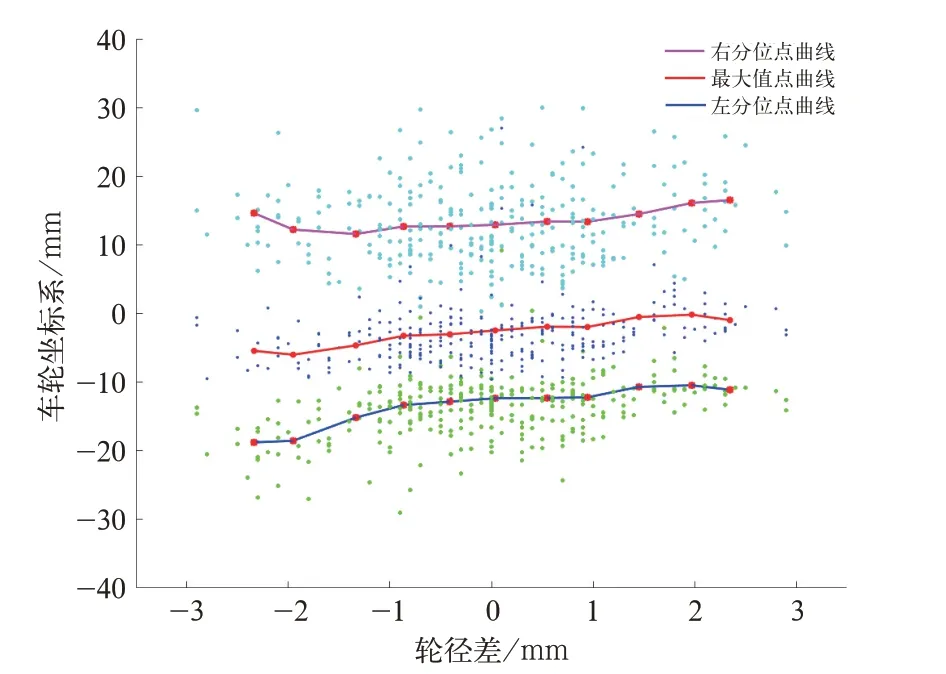
图5 轮径差对车轮磨耗位置变化规律

2.3 全廓形磨耗分位点的确定

在磨耗数据中很容易确定磨耗量最大值的相关信息，可以分析磨耗量变化规律，进一步确定磨耗宽度以及磨耗在车轮坐标系中的变化规律需分析确定分位系数R值。选取不同R值下的各分位点的分布情况，如图6 所示。

通过比较分析发现图6 中（a）和（b）中右分位点都存在不少超过分析区间［-40，30］的情况，因此R=0.75 和R=0.8 数 值 都 相 对 较 小，（c）和（d）都极少数点超过区间，R=0.85 和R=0.9 在分位点分布上分析相对R=0.75 和R=0.8 更加合理。初步分析后需最终确定效果相对最佳的R值，将不同R值得到的分位点曲线置于同一个图中比较得到，如图7 所示。

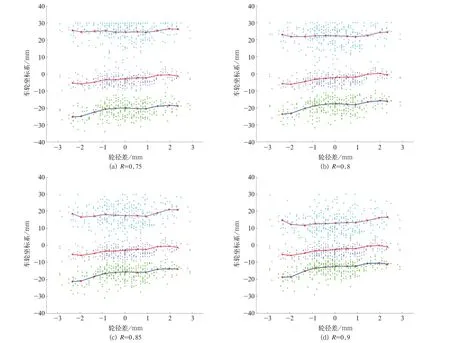
图6 不同R 值分位点分布图

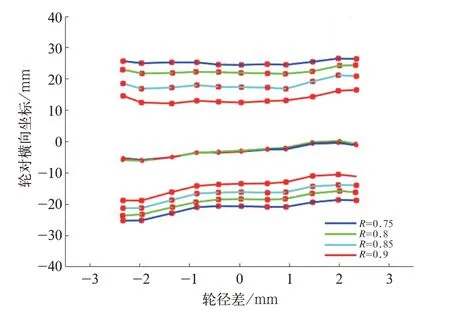
图7 不同R 值的分位曲线分析

随着R值的变化，左分位曲线几乎是等间距变化，R值的变化对左分位曲线的规律分析影响不大；可以明显看出右分位曲线变化明显，R=0.9 时考虑到右分位曲线靠近最大值曲线且容易造成其变化规律不明显，不便于观察磨耗宽度变化规律等问题。综合以上问题选择磨耗系数R=0.85。

3 不同因素对踏面磨耗的影响

在车轮材质确定的情况下，基于以上分析方法，分析轮对在不同轮径差以及不同轮位等条件下车轮的磨耗情况。

3.1 轮径差对踏面磨耗的影响

根据轮轨接触关系和磨耗理论分析得出：非独立传统轮对存在轮径差的情况下，运动状态下蠕滑力使轮对总是朝轮径值小的一侧横移以使左右车轮滚动圆直径DL=DR，磨耗区域总是朝着轮径值小的车轮轮缘部位移动，小轮径车轮踏面与轮缘磨耗呈增大趋势。

不同轮径差轮对磨耗规律如图8 所示，坐标轮径差为在同一轮对中当前车轮直径与另一车轮直径之差，轮径差为正数代表当前车轮在轮对中为大轮径，反之则为小轮径。分析图8 中不同轮径差对磨耗量和磨耗位置的影响：观察到在轮径差在1 mm 内磨耗量随轮径差变化影响不大，当轮径差大于特定值时，发现小轮径（轮径差为负值）车轮磨耗量随轮径差的变化呈现快速变化趋势，因此分析认为随着轮径差的增大，小轮径车轮磨耗会逐步增大，且轮径差越大这种现象就越明显。

图8 不同轮径差轮对磨耗规律

分析得到轮径差对轮对磨耗的影响主要是影响磨耗位置以及磨耗量：随着轮径差的增大，小轮径一侧车轮磨耗位置朝着靠近轮缘方向发展，同时对应的大轮径车轮磨耗位置朝着远离轮缘方向发展。针对上述分析中分段求平均值时包含一些极端数值点，需对数据进行一定的筛选排除并对拟合曲线进行平滑处理以避免过拟合现象。

最大磨耗值在轮对坐标系发生位置随轮径差的变化趋势进一步分析，包括：对轮径差分段正态拟合，光滑拟合正态均值点并平滑处理，分析平滑曲线变化趋势，如图9 所示。

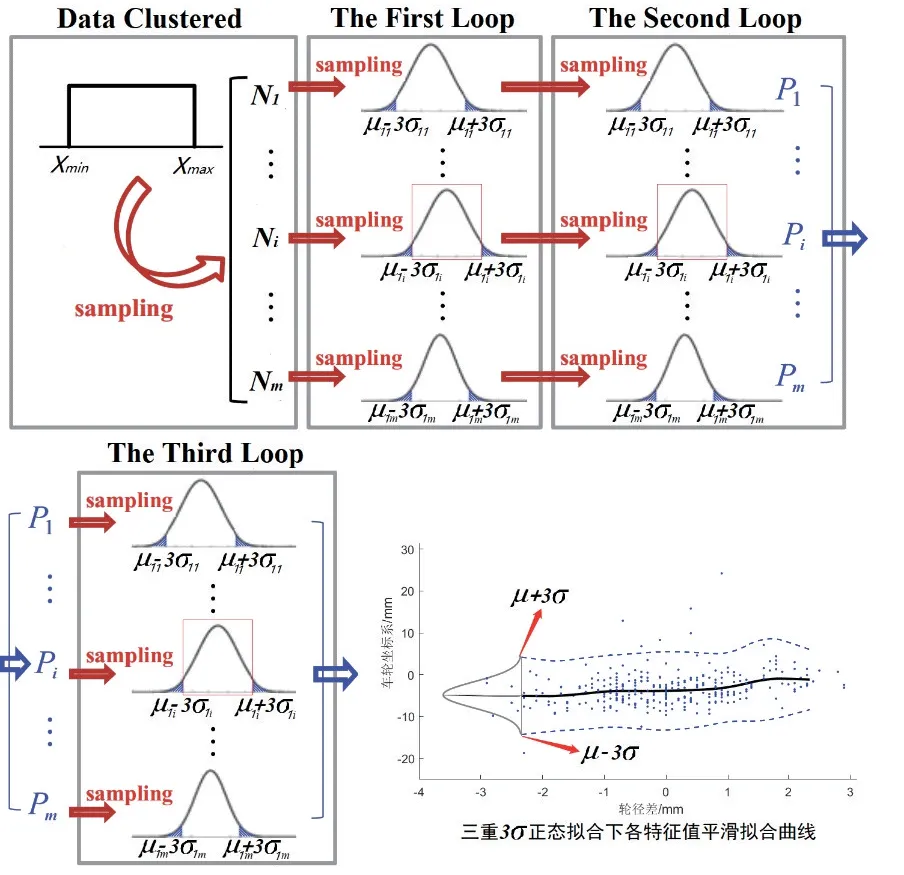
图9 三重3σ 正态拟合筛选下特征值平滑曲线

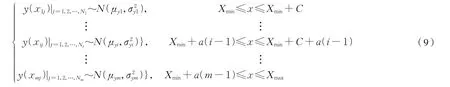
式中：y（xij）表示第i个分段区间内的第j个轮径差xij对应磨耗点的轮对横坐标位置。

通常有少部分数据点严重偏离，应对数据筛选剔除部分不合理数据点：首先对第i个分段区间内Ni个数据点正态分布拟合得到正态拟合均值μ1和正态拟合方差σ1，筛选数据满足式（10）条件的正态分布概率为99.74%，剔除小概率数据。

进行正态拟合3 次得到三重3σ（sigma）下正态拟合均值μ3和正态拟合方差σ3，将三重正态拟合均值μ3在坐标中光滑连接并作一次平滑处理后得到最大磨耗量发生位置随轮径差变化曲线，如图10 所示；同时，为了直观看出正态拟合下均值随轮径差变化的分布规律以及变化趋势快慢的分布情况，分析平滑后均值曲线得到图10 左上方正态拟合均值变化的斜率随轮径差的规律图。

从图10 中观察到均值变化的斜率在轮径差为0 附近时偏小且接近于0，可见磨耗位置变化不大；当轮径差大于1 mm 后能看到明显的最大磨耗位置发生移动，小轮径车轮一侧在轮径差1～2 mm范围内磨耗朝轮缘移动速度加快，而轮径差大于2 mm 后数据点较少且无3 mm 轮径差之后的数据，因此需要更多数据支撑后续规律研究；大轮径车轮磨耗随轮径差的变化朝远离轮缘位置的变化速率大于小轮径。

图10 最大磨耗量发生位置随轮径差变化规律分析

由以上分析，左分位点位置主要体现磨耗朝轮缘发展甚至磨轮缘的情况。正态均值斜率曲线表明轮径差为1.5 mm 左右时小轮径车轮的左分位点位置朝轮缘方向移动速度明显增大；轮径差在1 mm 内磨耗位置几乎影响不大，如图11 所示。由于缺少轮径差为3 mm 以上数据的支撑，目前无法通过数据分析得出更大轮径差的磨耗规律；且轮径差2 ～3 mm 之间数据量较少，相应的规律分析准确度有待后续大轮径差数据支持。

图11 左分位点位置随轮径差变化规律

此外，左右分位点间距在一定程度上可反映车轮踏面磨耗区域的宽度，间距越大则代表踏面磨耗宽度也就越大，反之踏面磨耗宽度就越小。拟合后车轮左右磨耗分位点间距随轮径差的变化规律，如图12 所示。可以发现，随着轮径差逐渐增大，小轮径一侧踏面磨耗宽度逐渐增大且变化速度明显大于同轮径差的大轮径车轮。

图12 拟合后左、右分位点间距随轮径差的分布规律

在轮对服役过程中，轮径差是车轮检修和旋修的一个重要指标。通过上述分析揭示轮对轮径差对车轮磨耗量和磨耗位置的影响规律，能够为轮对检修标准的制定提供参考指导。通过优化轮对轮径差检修限值，能够降低维修率、节约成本、提高轮对服役里程。需要指出的是，目前试验列车轮廓形数据量有限，在后续获得更为丰富的廓形数据后可以得到更为精确的磨耗量和磨耗位置随轮径差的演变规律，进一步为轮对轮径差检修限值制定提供参考和指导。

3.2 轮位对踏面磨耗的影响

在同一转向架中，前轮对由1、2 位车轮和车轴组成，后轮对由3、4 位车轮和车轴组成。若能揭示轮位对踏面磨耗的影响，可指导轮对的优化布置，降低车轮磨耗量，提高轮对服役里程。由于整列车中的车轮数据分析无法控制在同一个转向架跟踪分析，只能通过分析不同轮位在不同轮径差的条件下磨耗量以及磨耗位置的相关关系，对转向架的轮位进行分析，如图13 所示。

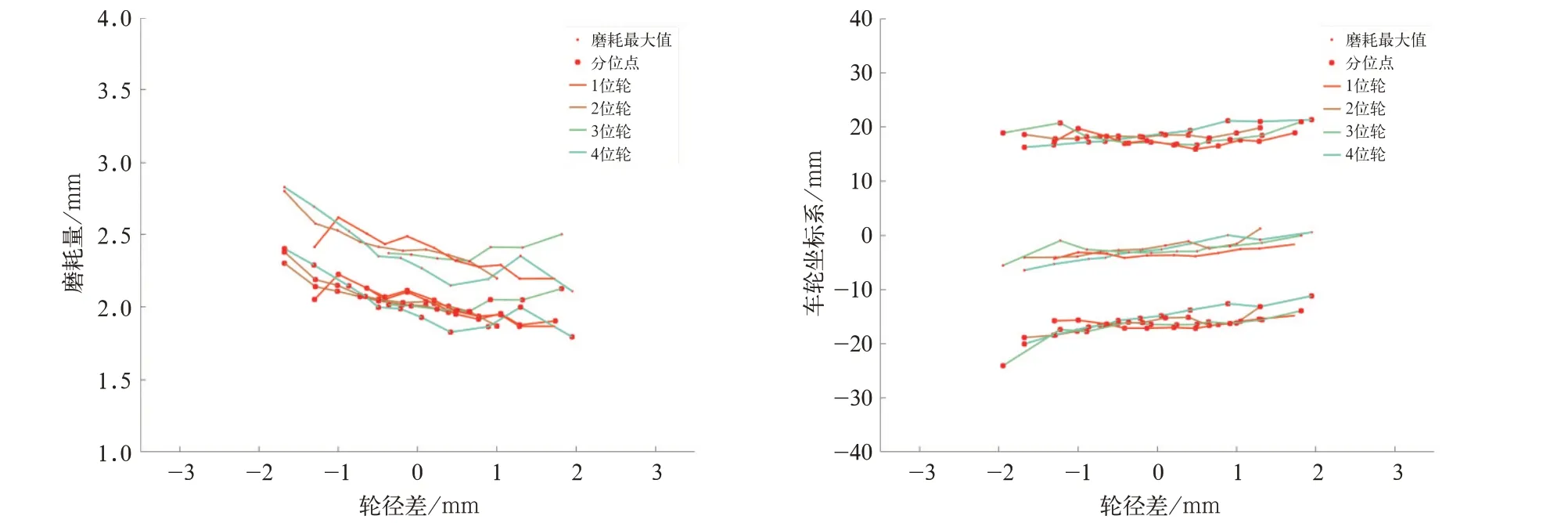
图13 轮径差下不同轮位的磨耗相关关系

通过分析图13 中不同轮位的磨耗量和磨耗位置随轮径差的变化趋势发现，车轮在转向架中所处的位置对车轮磨耗量以及磨耗位置未发现较强的影响关系。相比之下随着轮径差的变化，磨耗量及磨耗在车轮坐标系中发生位置有较强规律；按轮位分析得到各轮位随轮径差的磨耗规律与3.1 节中基本相似，各轮位之间无规律性差异。轮位对磨耗无较强的影响规律，文中对此暂不展开详细的分析，可通过后期对车轮磨耗的跟踪测试进一步确定其影响关系。

4 结 论

通过对测量的车轮廓形进行匹配分析，计算踏面磨耗量得到磨耗量曲线，进一步分析提取相关指标分析，可以得到以下结论：

（1）在铁路货车轮对存在轮径差的情况下，同一轮对中车轮磨耗主要表现在以下3 个方面：

（a）大轮径侧车轮踏面磨耗量相比小轮径侧车轮踏面磨耗量小，且随着轮径差的增大，大轮径车轮磨耗量变化不明显，小轮径车轮磨耗量在轮径差超过一定限值后增长明显。

（b）对于磨耗位置，随着轮径差增大，小轮径车轮踏面磨耗朝着靠近轮缘方向发展，轮径差超过一定限值后现象明显且有磨轮缘的趋势。

（c）左右磨耗分位曲线表明大小轮径车轮均随着轮径差增大而磨耗宽度增加，且小轮径车轮磨耗现象更严重。

（2）通过提出货车廓形匹配及其磨耗表征方法揭示车轮磨耗量和磨耗位置随轮径差的演变规律，综合考虑磨耗量和磨耗区域，得到分析结果能够为轮对检修限值的制定和优化提供参考和指导，通过控制轮径差来达到降低磨耗的目的，以此降低轮对耗材，从而实现一定的经济效益。

（3）分析不同轮位的磨耗量和磨耗位置随轮径差的变化规律发现，轮位对磨耗的影响不大，对不同的轮位数据分析未发现较强的相关性规律。若后续跟进分析重载货车中轮位对磨耗确无影响，在工程中轮位的搭配安装则不再需要考虑安装位置对磨耗的影响。

由于目前车轮廓形数据量有限，同时已获取数据轮径差局限在较小范围，且轮径差越大处在该状态的数据量急剧减少，影响车轮磨耗量和磨耗位置随轮径差的演变规律精确程度，后期将通过对车轮磨耗的进一步跟踪测试来确定其影响关系，并为轮对检修提供更为明确的参考和指导。