不可逆往复式Brayton循环性能分析与优化:(1)功率密度分析
施双双,戈延林,陈林根
(1.武汉工程大学 热科学与动力工程研究所,武汉 430205;2.湖北省绿色化工装备工程技术研究中心,武汉430205;3.武汉工程大学 机电工程学院,武汉 430205)
在有限时间、有限速率和有限尺寸约束下,对热力过程和循环进行分析和优化一直是现代热力学理论的研究重点领域之一,其代表性的理论为有限时间热力学理论[1-6]。近年来,有限时间热力学理论已经被广泛应用于定常流[7-11]和往复式[12-15]Brayton循环的性能分析和优化中,众多学者对循环功率[8,12-15]、效率[7,12-15]、生态学函数[9]和利润率密度[10]等目标函数的最优性能进行了研究。
除以上目标函数外,郑军林等[16-17]和陈林根等[18-19]将功率密度这一目标函数(功率与最大质量体积之比)引入到内可逆[16-17]和不可逆[18-19]定常流Brayton循环中,分析了高、低温侧换热器的最佳热导率分配和工质热容率对循环功率密度最优性能的影响,并将循环在最大功率密度时得到的最大质量体积比、最大压比和热效率与循环在最大功率时得到的结果相比较,结果表明定常流Brayton循环在以最大功率密度为设计准则时,具有效率更高、尺寸更小的特点。
文献[14]建立了一类考虑传热和摩擦损失的不可逆往复式Brayton循环模型,研究了其功率和效率的最优性能。本文在文献[14]建立的循环模型基础上,进一步考虑循环中存在的内不可逆性损失,引入目标函数——功率密度,研究循环的功率密度最优性能,分析循环最大温比和3种损失对循环功率密度最优性能的影响,并比较循环在最大功率和最大功率密度条件下相应的最大质量体积比、最大压比和热效率,旨在对实际热机的设计提供参考。
1 循环模型和主要性能解析式
图1为不可逆往复式Brayton循环模型的T-s图和P-v图,1→2为不可逆压缩过程,2→3为定压吸热过程,3→4为不可逆膨胀过程,4→1为定压放热过程,1→2s为等熵压缩过程,3→4s为等熵膨胀过程。
循环中工质的吸热率为:
(1)
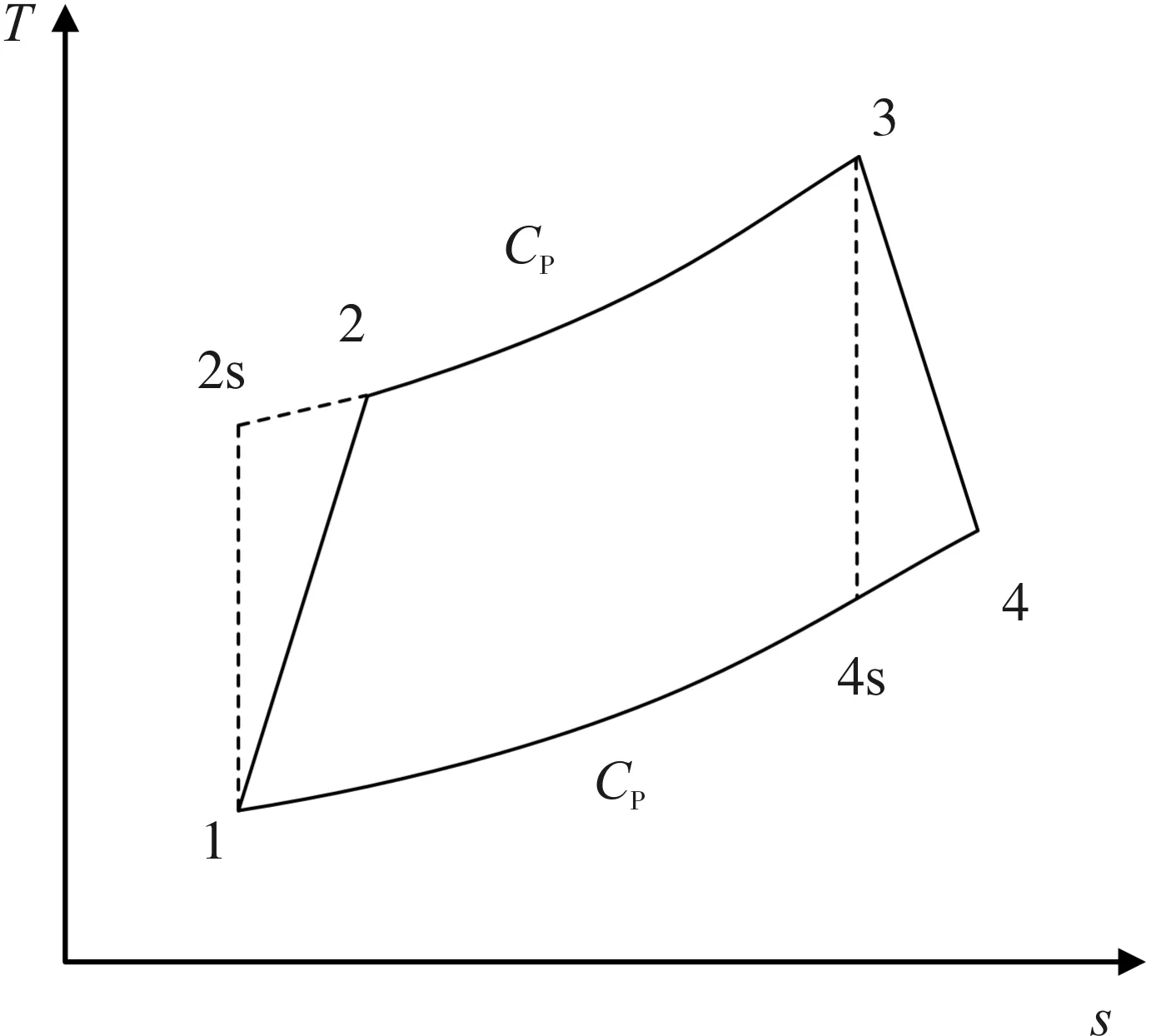
(a)T-s图
循环中工质的放热率为:
(2)
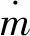
对于2个不可逆绝热过程1→2和3→4,由不可逆压缩和膨胀效率表示过程中存在的内不可逆性损失:
ηc=(T2s-T1)/(T2-T1)
(3)
ηe=(T4-T3)/(T4s-T3)
(4)
定义循环压缩比γ和最大温比τ分别为:
γ=V1/V2
(5)
τ=T3/T1
(6)
对于循环的不可逆绝热过程1→2和3→4有:
[ηc(T2-T1)+T1]k-T1(γT2)k-1=0
(7)
(8)
实际循环中,工质燃烧时与气缸之间产生传热损失,活塞在气缸壁内运动时与气缸壁之间产生摩擦损失。根据文献[14]对Brayton循环传热损失和摩擦损失的处理方式,传热损失率和摩擦损失消耗的功率可分别表示为:
(9)
Pμ=4μ(4Ln)2=64μ(Ln)2
(10)
式中:B为传热损失系数;μ为摩擦损失系数;T0为环境温度;L为活塞长度;n为转速。
循环的输出功率为:
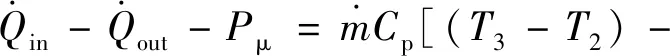
(T4-T1)]-64μ(Ln)2
(11)
循环的热效率为:
(12)
定义循环的总体积vt、冲程体积vs和间隙体积vc分别为:
vt=vs+vc
(13)
vs=πd2L/4
(14)
vc=πd2L/4(γ-1)
(15)
对于往复式Brayton循环,vt=vmax=v4,由式(5)和式(13)至(15)可以得到循环功率密度,为:

(T4-T1)]-64μ(Ln)2}/(πd2Lγ)
(16)
不可逆往复式Brayton循环中存在的传热、摩擦、内不可逆性损失和排气冲程排往环境产生的熵产率分别表示为:
σq=B(T2+T3-2T0)[1/T0-2/(T2+T3)](17)
σμ=Pμ/T0=64μ(Ln)2/T0
(18)
(19)
(20)
(21)
因此整个循环的熵产率为:
σ=σq+σμ+σ2s→2+σ4s→4+σpq=B(T2+
T3-2T0)[1/T0-2/(T2+T3)]+
循环的生态学函数为:
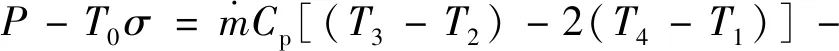
B(T2+T3-2T0)[1-2T0/(T2+T3)]-
(23)
定义无因次功率、无因次功率密度和无因次生态学函数分别为:
(24)
(25)
(26)
当循环初始温度T1、循环温比τ、压缩比γ、不可逆压缩和膨胀效率ηc和ηe给定时,可以由式(7)解出T2,由式(6)解出T3,最后再由式(8)解出T4,将解出的T2、T3和T4代入式(11)、(12)、(16)和(23)得到相应的功率、效率、功率密度和生态学函数。
2 功率密度性能分析



图2 τ对性能的影响
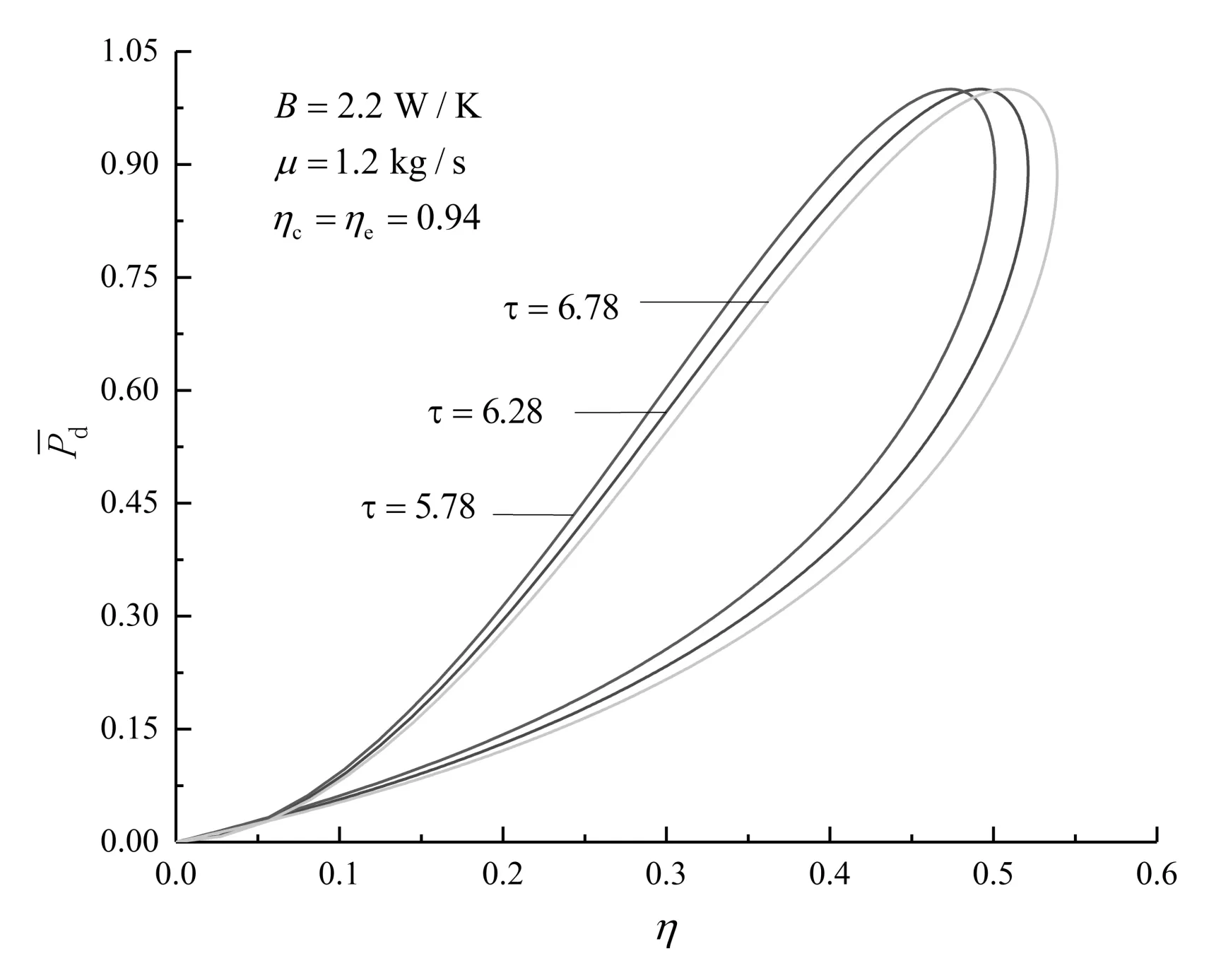
图3 τ对性能的影响

图4 μ、ηe和ηc对性能的影响

图5 μ、ηe、ηc和B对性能的影响
3 最大功率和最大功率密度准则下的性能比较
图6至图8给出了不可逆往复式Brayton循环在最大功率和最大功率密度准则下的最大质量体积比、最大压比和热效率随循环最大温比的变化关系。从图6和图7可以看出,与最大功率准则下对应的结果相比,最大功率密度准则下对应的最大质量体积比更小,最大压比更大,说明以最大功率密度为基准设计的发动机的设计尺寸更小。

图6 v4/vs 与τ的曲线

图7 p3/p1 与τ的曲线
从图8可以看出,最大功率密度准则下循环的热效率更高,当τ=6.28时,最大功率对应的效率为46.82%,最大功率密度对应的效率为49.17%,后者比前者增加了5.02%。由此可知,与最大功率准则相比,在最大功率密度准则下设计的发动机拥有更小的尺寸和更高的热效率。

图8 η与τ的曲线
4 结 论
本文在文献[14]建立的不可逆往复式Brayton循环模型基础上,引入功率密度目标函数,研究了不可逆往复式Brayton循环的功率密度最优性能,分析了循环温比、传热损失、摩擦损失和内不可逆性损失对该循环功率密度与压缩比和功率密度与效率特性的影响,比较了该循环在最大功率与最大功率密度准则下对应的最大质量体积比、最大压比和热效率。结果表明:

2)基于最大功率密度准则设计的发动机比基于最大功率准则设计的发动机尺寸更小,效率更高。

