方形巷道围岩拉剪破裂网络发育及演化规律

郭钇君，洛 锋,2,3，李 盟,2,3，孙 赓，刁杨龙，续培东

( 1. 河北工程大学 矿业与测绘工程学院，河北 邯郸 056038；2. 河北省煤炭矿井建设技术创新中心，河北 邯郸 056038；3. 邯郸市深部巷道围岩控制及灾害防治重点实验室，河北 邯郸 056038 )

随着矿产资源的开发利用逐渐向深部转移以及掘支一体机的广泛使用，大断面矩形巷道在煤矿安全高效生产中得到了广泛应用。深部矩形巷道开挖后，在高地应力的影响下，多数煤层巷道围岩会出现严重的变形与破坏。为了对矩形巷道围岩变形与破坏进行精准靶向支护，需准确掌握矩形巷道围岩松动破坏圈内的拉剪破裂机制及发育规律。靶向支护不同于以往经验化及均一化的锚固支护方法，其为充分考虑岩体破裂方向、形态以及破裂性质的一种深部软岩巷道精准靶向锚注控制方法。在高地应力条件下，巷道围岩呈现显著方向性的张拉、剪切破断和持续变形等特性，通过理论和试验研究可以获得并掌握巷道围岩拉伸-剪切裂隙的空间展布特征，采用具有一定目标性、方向性的锚网索支护和注浆加固技术，能够高效地实现巷道支护“对定向破裂的定向控制”，从而实现精准靶向支护。因此，深入研究方形巷道围岩拉剪裂纹萌生和演化规律对实现巷道围岩精准靶向控制具有重要意义。

对于巷道围岩破坏的研究，国内许多学者对圆形巷道围岩应力及塑性区分布进行了大量的研究[1-5]。GE Decheng[6]等分析了方形巷道围岩应力分布、塑性区发育、弹性能量密度、局部能量释放率( LERR )等规律和总能量释放规律；侯公羽[7]等使用水泥砂浆浇筑胚体并加工成矩形巷道围岩试件，进行开挖卸荷模型试验，得到了顶板、隅角和帮部围岩的变形破坏特征以及 AE 撞击计数、损伤变量、频谱的演化特点；于远祥[8]等运用深基点多点位移和钻孔窥视相结合的方法，得到了不同岩性条件下矩形巷道围岩松动范围与巷道埋深、断面尺寸、围岩强度及考虑各影响因素的不同预测公式；李廷春[9]等通过数值模拟研究，得出受断面及岩性影响，矩形巷道会提前进入塑性范围；宫凤强[10]等采用TRW-3000 岩石真三轴电液伺服诱变试验机对花岗岩材料加工的含预制矩形孔洞的立方体试样进行模拟试验，得出了深部硬岩矩形隧洞围岩板裂破坏的发生机制；刘迅[11]等分析了不同埋深、巷道高宽比、侧压系数对围岩塑性区的影响。对于巷道围岩应力的研究，王宏伟[12]等建立了非静水压力条件下巷道围岩应力状态分析的力学模型，得出了非静水压力条件下圆形巷道围岩破碎区及塑性区的应力与位移的解析解。国内外学者经常采用复变函数的方法构建矩形巷道的复应力函数以得出矩形巷道围岩应力理论解[13-18]。对于相似材料模拟试验方面的研究，段昌瑞[19]等开展了4种工况下硐室的模拟试验，揭示了巷道发生分区破坏的条件；靖洪文[20]等通过相似材料模拟试验，探讨分析了围岩松动圈测试与深部巷道大松动圈围岩支护中存在的技术难题及应对措施。

目前，对于方形巷道围岩变形破坏规律的研究已有较为成熟的结论，但大多停留在对围岩塑性区范围的研究方面。笔者在前人研究的基础上，采用有限元数值模拟试验以及相似材料模拟试验，建立静水压力下平面应变方形巷道，对不同埋深条件下方形巷道围岩塑性区内拉剪破裂初始位置、剪切破裂长度、方向变化及拉剪破裂网络进行深入研究，研究成果可为实际工程中巷道围岩靶向支护提供理论基础。

1 问题的提出

在现场观测和理论研究中，圆形硐室围岩产生塑性剪切破坏已经被证明，巷道在开挖后围岩应力重新分布，径向应力迅速降低，切向应力迅速增大，当应力达到围岩强度时，围岩中形成了拉剪破裂区域，圆形巷道围岩拉剪破裂示意如图1所示。

图1 圆形巷道拉剪破裂Fig. 1 Tension-shear failure of circular roadway

在侧压系数为1时，最大主应力迹线呈环状分布，围岩剪切破裂呈滑移线分布，并与最大主平面成45°+φ2的角度逐渐向深部扩展发育，拉破裂主要沿最大主应力迹线发育。为了阐述方形巷道围岩拉剪破裂形成及发育规律，笔者以侧压系数λ=1时对方形巷道进行数值模拟试验以及相似材料模拟试验，并与圆形巷道围岩破裂进行对比，以便更好地说明方形巷道围岩拉剪破裂发育趋势及演化规律。

2 模型的建立及变量的选择

2.1 模型设定

通过FLAC3D数值模拟软件建立长×高×宽为30 m×30 m×1 m的以平面应变为模型的方形巷道，巷道断面为4 m×4 m，根据矿山压力重分布规律，巷道开挖后应力最大影响半径为13 m，模型半径设置为15 m，以消除边界对巷道围岩应力重分布的影响。为了监测围岩应力变化分布情况，分别在巷道右帮和右顶角围岩7 m范围内设立14个应力监测点，巷道数值模型尺寸及应力监测点位置如图2所示。

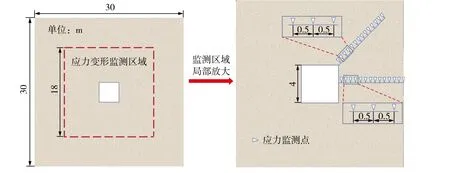
图2 方形巷道建模Fig. 2 Modeling of square roadway

2.2 参数设定

巷道所在岩层为砂岩，其参数见表1[21]。为获得围岩峰后破坏特征，在FLAC3D数值模拟软件中采用应变软化本构模型。应变软化是材料塑性屈服后的非静态过程，塑性屈服后的材料峰后力学性质对岩体的力学行为影响很大。在FLAC3D数值模拟中，随着黏聚力和内摩擦角的逐渐减小，材料的承载能力逐渐减弱。对于地下工程，岩体达到峰值强度时并不完全失去承载能力，其承载能力随着变形的增加而逐渐降低，表现为强度参数的弱化。

表1 岩体力学参数[21]Table 1 Mechanical parameters of rock mass[21]

砂岩应变软化相关参数及其参数弱化规律见表2。

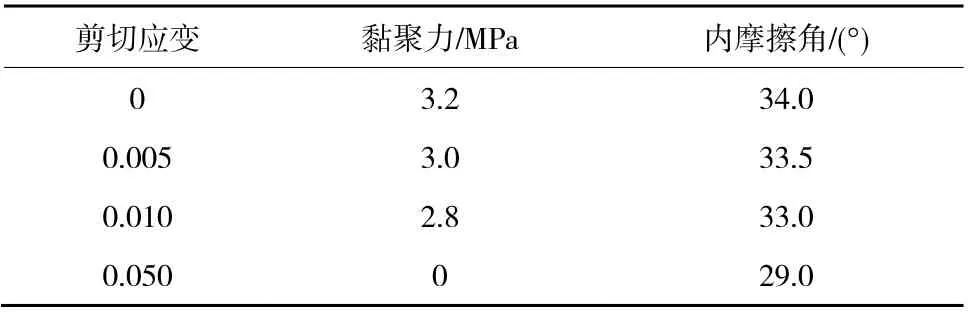
表2 应变软化参数及其弱化规律Table 2 Strain softening parameters and weakening law of sandstone

2.3 加载方案设定

为获得不同埋深条件下方形巷道围岩拉剪破裂网络的形成及发育过程，在巷道处于埋深分别为400，600，800，1 000，1 100，1 200 m时，研究巷道围岩破裂网络的形成及发育规律，其所对应的垂直应力 Vσ和水平应力 Hσ见表3。

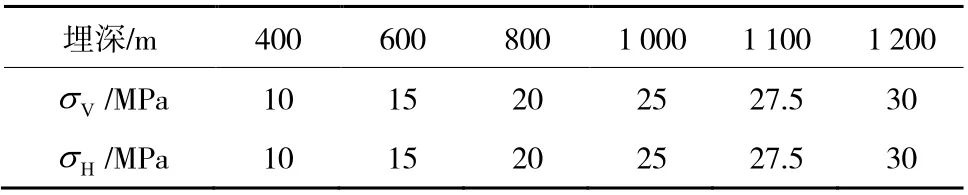
表3 围岩应力条件Table 3 Stress conditions of surrounding rock

3 方形巷道围岩破裂网络演化规律

3.1 巷道围岩拉剪破裂网络演化规律

当埋深为400 m时，由于方形巷道孔边围岩发生应力重新分布，在巷道4个角点产生集中应力，如图3( a )所示；当集中应力超过岩体强度时，方形巷道4个角点形成了剪切破裂，即剪切带发育起点Ⅰ，如图4( a )所示。随着埋深增加至600 m，4个角点形成的剪切破裂相互贯通发育，绕轴旋转方形剪切破裂网络在巷道围岩形成并在埋深800 m时充分发育，如图4( b )～( c )所示。

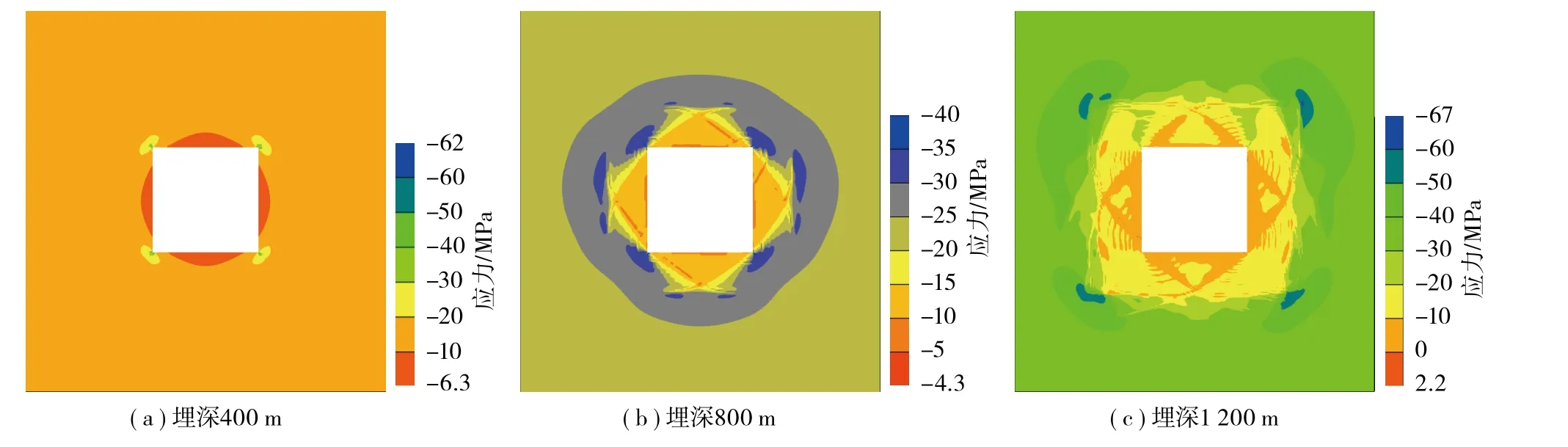
图3 方形巷道围岩最大主应力分布Fig. 3 Distribution of maximum principal stress in surrounding rock of square roadway

图4 方形巷道围岩松动圈内拉剪破裂分布Fig. 4 Distribution of tension-shear failure in loose circle of surrounding rock in square roadway

由图3～4可知，当埋深800 m时，在方形剪切破裂网络Ⅰ的4个角点出现集中应力并形成明显的方形最大主应力( 图3( b ) )，同时在方形剪切破裂网络Ⅰ的4个角点产生与最大主平面成45°+φ2角度的剪切破裂，即剪切带发育起点Ⅱ；当埋深为1 000 m时，在方形剪切破裂网络Ⅰ的边界处产生了明显的拉破坏；当埋深增加至1 100 m时，剪切破裂相互贯通并充分发育，继续以方形绕轴旋转方式向深部围岩扩展，形成方形剪切破裂网络Ⅱ，如图4( e )所示；当埋深1 200 m时，巷道方形剪切破裂网络Ⅱ4个角点产生高集中应力( 图3( c ) )，此时剪切破裂继续在方形剪切破裂网络Ⅱ的4个角点形成，即剪切带发育起点Ⅲ，如图4( f )所示。拉破裂在方形剪切破裂网络Ⅰ边界处充分发育，并随着埋深的增加逐渐向围岩深部扩展。

3.2 巷道围岩应力演化规律

图5为巷道切应力曲线分布。由图5( a )可知，当巷道埋深为400 m时，巷道开挖使得围岩应力重新分布，应力向4个角点转移，并在4个角点处产生集中应力，因此在巷帮并未出现明显的应力峰值和应力卸压；当巷道埋深为600 m时，由于方形剪切破裂网络的形成，应力向新产生的方形剪切破裂网络的4个角点转移，因此巷帮围岩出现明显的应力集中现象；当巷道埋深为800 m时，峰值应力进一步增大并出现在方形剪切破裂网络Ⅰ的4个角点处；当巷道埋深为1 000 m时，巷道浅部围岩卸压相对严重，并随着埋深的增加，浅部围岩卸压更加充分；当巷道埋深为1 100，1 200 m时，由于围岩卸荷，巷道集中应力向方形剪切破裂网络Ⅱ的4个角点转移，因此巷帮峰值应力并无明显变化。

图5 方形巷道围岩应力曲线分布Fig. 5 Stress curves distribution of surrounding rock in square roadway

由图5( b )可知，当巷道埋深为400 m时，巷道右上角由于出现集中应力，围岩发生破坏造成卸压；当巷道埋深为1 200 m时，方形剪切破裂网络Ⅱ的4个角点产生明显的集中应力；通过应力曲线发现，随着埋深的增加，集中应力由方形巷道4个角点产生，向方形剪切破裂网络的4个角点转移，从应力方面解释了方形剪切破裂网络的形成及发育过程。

4 方形巷道围岩破裂相似模拟试验

4.1 试验原理

4.1.1 相似材料模拟试验台

在物理模型建模时，首先根据平面应变问题限制模型边界变形；其次要实现物理模型的双向加载。根据上述条件，自行研制了双向加载试验台，试验台模型如图6所示，试验设备分为框架系统和加载系统。框架系统主要由主体钢架、前后挡板、上加载板、侧加载板以及支撑木架等组成。前挡板采用有机玻璃板以便观察巷道围岩变形；后挡板采用槽钢，因为模型巷道从后向前开挖，因此在开挖处的槽钢预留开挖孔；支撑木架用来装填相似材料时支撑侧压板。加载系统包括液压泵和千斤顶，分别对模型的水平和垂直方向进行加载。通过“先加载后开挖”的试验方法，在不同的埋深条件下，对方形巷道围岩破裂特征演化规律进行研究，试验的水平应力值与垂直应力值见表3。通过加载系统对相似材料模型施加对应的水平和垂直载荷，观察试验前对相似材料打出的墨线网格变化，获得方形巷道围岩的变形破坏特征。

图6 相似模拟试验台Fig. 6 Similar material simulation experiment bench

4.1.2 相似模拟判据

相似材料的配比应尽量符合相似模拟方法的相似判据，物理模型边界施加载荷应符合相似模拟方法中单质条件里的初始条件，因此，根据试验台尺寸特点，设计尺寸相似比为1∶50，原方形巷道尺寸为4 m×4 m，巷道模型尺寸为80 mm×80 mm；容重相似比为1.5；应力相似比为75。

4.2 相似材料配比试验

正确选择相似材料并确定相似配比是相似模型是否能准确反映工程原型客观规律的关键因素之一。笔者通过查阅资料，最终确定采用沙子、石膏、石灰、水泥等材料进行相似配比试验。为了获得砂岩的相似材料力学参数，对多种不同配比材料进行对比试验。通过单轴伺服试验台进行单轴压缩，获得不同配比材料的单轴抗压强度、弹性模量等参数，根据上述相似模拟判据，选择最佳相似材料配比。通过对不同配比号的细沙、石膏及水泥材料试件和细沙、石膏及石灰材料试件进行大量力学性能测试，最终确定以细沙、石膏和石灰作为主要材料进行相似材料模拟试验，具体参数见表4。

表4 相似材料力学参数Table 4 Mechanical parameters of similar materials

4.3 方形巷道围岩破裂网络特征分析

方形巷道围岩破裂相似材料模拟试验结果如图7所示。

当埋深为400 m时，首先在顶底板的4个角点发生较为明显的剪切破裂，顶底板呈现显著的锥形剪切破裂( 图7( a ) )；当埋深为600 m时，顶板和左帮均出现新的剪切破裂，并发现两者相互贯通，通过墨线网格的变化以及剪切破裂出现的位置可以判断巷道围岩塑性区近似呈方形，巷道内部分别出现片帮和顶板冒落的现象( 图7( b ) )；当埋深为800 m时，顶底板出现新的剪切破裂，两帮的剪切滑移破裂愈加明显，巷道片帮现象严重，底板出现突出现象( 图7( c ) )；当埋深为1 000 m时，巷道顶板和帮部剪切裂隙进一步发育贯通( 图7( d ) )，巷道片帮和顶板冒落严重；当埋深为1 100 m时，巷道帮部围岩及底板均出现新的剪切破裂( 图7( e ) )，且破裂贯通现象更为明显，根据墨线网格线的变化可知，巷道围岩帮部及顶底板围岩出现向巷道内部挤压的严重变形，巷道严重破坏；当埋深为1 200 m时，围岩变形加剧，围岩破裂愈加明显，巷道接近闭合，根据剪切破裂的位置以及巷道围岩的变形可以准确判断巷道围岩塑性区近似呈方形( 图7( f ) )。

图7 不同埋深下方形巷道相似材料模拟试验结果Fig. 7 Similar material simulation experiment results of square roadway under different depth

在相似材料模拟试验中，因为模型单向加载导致模型加载端一侧与固定端一侧受力存在误差，所以巷道左帮与右帮裂隙发育不对称。根据相似材料模拟试验结果，巷道围岩破裂扩展发育规律与数值模拟试验基本一致，一方面验证了数值模拟的正确性；另一方面为地下空间方形巷道采掘活动提供了理论与试验支撑。

5 讨 论

( 1 ) 地下岩体在开挖前处于原岩应力状态，巷道开挖使得原有的应力平衡被打破，巷道围岩出现增压与卸荷，对于方形巷道更为明显。在数值模拟与相似材料模拟试验的基础上，获得了方形巷道围岩拉剪破裂形成及演化规律。

( 2 ) 方形巷道开挖卸荷后，塑性区Ⅰ首先在围岩中形成，随着埋深的增加，塑性区Ⅱ逐渐在围岩中形成，如图8所示，方形巷道开挖是塑性区Ⅰ形成的基础，塑性区Ⅰ的破坏形态相当于形成了更大的方形巷道，是塑性区Ⅱ形成的基础。

图8 方形巷道剪切破裂概念化模型Fig. 8 Conceptual model of shear failure in square roadway

( 3 ) 方形巷道开挖造成4个角点发生应力集中，使得主剪切破裂Ⅰ在4个角点形成并发育，随着主剪切破裂Ⅰ的发育贯通，次生剪切破裂Ⅰ开始在巷帮及顶底板发育，形成剪切破裂网络Ⅰ，即塑性区Ⅰ。埋深增加使得剪切破裂网络Ⅰ的4个角点的主剪切破裂Ⅱ扩展发育，随着主剪切破裂Ⅱ的发育贯通，次生剪切破裂Ⅱ逐渐发育，形成剪切破裂网络Ⅱ，即塑性区Ⅱ。

( 4 ) 根据数值模拟试验及相似材料试验发现，主剪切破裂Ⅰ和Ⅱ的发育贯通是塑性区Ⅰ和Ⅱ边界形成的重要条件，在不同的主应力方向以及不同的岩性条件下，主剪切破裂和次生剪切破裂的发育也会呈现出不同的形态，但随着最大主应力方向的变化，剪切破裂发育方向与最大主应力平面夹角均呈45°+φ2。

6 结 论

( 1 ) 方形巷道围岩拉剪破裂演化是一个渐进的过程，随着埋深的增加，拉破裂与剪破裂网络呈绕轴旋转方形的方式向深部巷道围岩扩展演化，剪破裂由巷道4个角点形成并呈剪切滑移方式发育扩展，拉破裂主要沿方形巷道围岩主应力迹线扩展发育。

( 2 ) 随着埋深的增加，巷帮切向应力曲线的应力卸压区逐渐增大，当埋深为1 000 m时，巷道围岩卸压充分，集中应力逐渐增大并向深部围岩转移，集中应力在方形巷道4个角点产生并向方形剪切破裂网络的4个角点转移，获得了方形巷道围岩应力的演化规律。

( 3 ) 通过自行研制的双轴加载试验台对方形巷道进行相似材料模拟试验，发现在埋深400 m时，剪切破裂首先出现在方形巷道的4个角点，随着埋深的增加，顶底板和两帮浅部围岩由于位于受拉区域，因此出现愈加严重的顶板冒落、底臌、片帮等现象，深部围岩出现剪切破裂并逐渐发育贯通。

( 4 ) 通过相似材料模拟试验与数值模拟试验的对比，发现两者围岩破裂形态基本一致，验证了数值模拟试验的正确性与科学性，据此提出方形巷道围岩拉剪破裂网络及塑性区形态发育规律的概念化模型，为实现方形巷道的靶向支护方法提供理论参考。

参考文献( References )：

[1] 马念杰，马骥，赵志强，等. X型共轭剪切破裂-地震产生的力学机理及其演化规律[J]. 煤炭学报，2019，44( 6 )：1647-1653.MA Nianjie，MA Ji，ZHAO Zhiqiang，et al. Mechanical mechanism and evolution of X-shaped conjugate shear fractures-seism[J]. Journal of China Coal Society，2019，44( 6 )：1647-1653.

[2] 白雪元，王学滨，马冰，等.不同围压时含孔洞模型裂缝扩展的连续-非连续数值模拟[J].地质力学学报，2019，25( 2 )：240-248.BAI Xueyuan，WANG Xuebin，MA Bing，et al. Simulation of the crack propagation for the model with a hole under different confining pressures based on a continuum-discontinuum method[J]. Journal of Geomechanics，2019，25( 2 )：240-248.

[3] 王卫军，董恩远，袁超.非等压圆形巷道围岩塑性区边界方程及应用[J].煤炭学报，2019，44( 1 )：105-114.WANG Weijun，DONG Enyuan，YUAN Chao. Boundary equation of plastic zone of circular roadway in non-axisymmetric stress and its application[J]. Journal of China Coal Society，2019，44( 1 )：105-114.

[4] 洛锋，杨本生，孙利辉，等.高垂直应力状态下巷道围岩分区破坏特征试验研究[J].采矿与安全工程学报，2012，29( 4 )：497-504.LUO Feng，YANG Bensheng，SUN Lihui，et al. Experimental research on the failure characteristics of surrounding rock under high vertical ground stress[J]. Journal of Mining & Safety Engineering，2012，29( 4 )：497-504.

[5] 董海龙，高全臣，张赵，等. 两向不等压巷道围岩塑性区近似解及数值模拟[J].煤炭学报，2019，44( 11 )：3360-3368.DONG Hailong，GAO Quanchen，ZHANG Zhao，et al. Approximate solution and numerical simulation for plastic zone of roadway surrounding rock under unequal compression in two directions[J].Journal of China Coal Society，2019，44( 11 )：3360-3368.

[6] GE Decheng，JIANG Fuxing，WANG Cunwen，et al. Sliding impact mechanism of square roadway based on complex function theory[J].Shock and Vibration，2021，2：1-12.

[7] 侯公羽，荆浩勇，梁金平，等.不同荷载下矩形巷道围岩变形及声发射特性试验研究[J].岩土力学，2020，41( 6 )：1818-1828.HOU Gongyu，JING Haoyong，LIANG Jinping，et al. Experimental study on surrounding rock deformation and acoustic emission characteristics of rectangular roadway under different loads[J]. Rock and Soil Mechanics，2020，41( 6 )：1818-1828.

[8] 于远祥，谷拴成.矩形巷道围岩松动范围实测及控制技术研究[J].采矿与安全工程学报，2013，30( 6 )：828-835.YU Yuanxiang ，GU Shuancheng. Measurement of loosened surrounding rock scope in the rectangular roadway and its control techniques research[J]. Journal of Mining & Safety Engineering，2013，30( 6 )：828-835.

[9] 李廷春，卢振，刘建章，等.泥化弱胶结软岩地层中矩形巷道的变形破坏过程分析[J].岩土力学，2014，35( 4 )：1077-1083.LI Tingchun，LU Zhen，LIU Jianzhang，et al. Deformation and failure process analysis of rectangular roadway in muddy weakly cemented soft rock strata[J]. Rock and Soil Mechanics，2014，35( 4 )：1077-1083.

[10] 宫凤强，伍武星，李天斌，等.深部硬岩矩形隧洞围岩板裂破坏的试验模拟研究[J].岩土力学，2019，40( 6 )：2085-2098.GONG Fengqiang，WU Wuxing，LI Tianbin，et al. Simulation experimental study of spalling failure of surrounding rock of rectangular tunnel of deep hard rock[J]. Rock and Soil Mechanics，2019，40( 6 )：2085-2098.

[11] 刘迅，王卫军，吴海，等.矩形巷道围岩塑性区扩展规律分析[J].矿业工程研究，2017，32( 1 )：14-18.LIU Xun，WANG Weijun，WU Hai，et al. On expansion regularity of plastic zone of surrounding rock in rectangular tunnel[J]. Mineral Engineering Research，2017，32( 1 )：14-18.

[12] 王宏伟，张登强，邓代新，等.非静水压力条件下巷道围岩破碎区应力分布特征[J].煤炭学报，2020，45( 11 )：3717-3725.WANG Hongwei，ZHANG Dengqiang，DENG Daixin，et al. Stress distribution characteristics of roadway surrounding rock damaged zone under non-hydrostatic pressure[J]. Journal of China Coal Society，2020，45( 11 )：3717-3725.

[13] 廖向阳，谭小华，李青锋.厚煤层矩形巷道应力分布及支护对策研究[J].矿业工程研究，2011，26( 1 )：1-6.LIAO Xiangyang，TAN Xiaohua，LI Qingfeng. Research on stress distribution and supporting countermeasures of rectangular roadway in thick coal seam[J]. Mineral Engineering Research，2011，26( 1 )：1-6.

[14] 吴帅，刘淑红，段思阳.矩形巷道围岩应力分布的复变函数解[J].煤矿安全，2019，50( 1 )：219-221，225.WU Shuai，LIU Shuhong，DUAN Siyang. Complex function solution of stress distribution in surrounding rock of rectangular roadway[J].Safety in Coal Mines，2019，50( 1 )：219-221，225.

[15] 茹锐锋，于雁武，贾康辉，等.矩形巷道岩爆危险性受侧压系数的影响研究[J].中北大学学报( 自然科学版 )，2021，42( 2 )：117-122.RU Ruifeng，YU Yanwu，JIA Kanghui，et al. Research on the influence of lateral pressure coefficient on the rockburst hazard of rectangular roadway[J]. Journal of North University of China ( Natural Science Edition )，2021，42( 2 )：117-122.

[16] 刘灯凯，饶军应，聂崇欣，等.深埋矩形巷道围岩压力拱变化规律研究[J].矿业研究与开发，2020，40( 5 )：108-112.LIU Dengkai，RAO Junying，NIE Chongxin，et al. Study on variation law of surrounding rock pressure arch in deep rectangular roadway[J].Mining Research and Development，2020，40( 5 )：108-112.

[17] 王志强，武超，石磊，等.基于复变理论的双向不等压圆形巷道围岩应力及塑性区分析[J].煤炭学报，2019，44( S2 )：419-429.WANG Zhiqiang，WU Chao，SHI Lei，et al. Analysis of surrounding rock stress and plastic zone of two-way unequal pressure circular roadway based on complex variable theory[J]. Journal of China Coal Society，2019，44( S2 )：419-429.

[18] ZHAO Guangpu，YANG Shengli. Analytical solutions for rock stress around square tunnels using complex variable theory[J]. International Journal of Rock Mechanics & Mining Sciences，2015，80( 14 )：302-307.

[19] 段昌瑞，郑群，薛俊华，等.不同工况下深部围岩分区破坏非连续变形试验研究[J].采矿与岩层控制工程学报，2021，3( 4 )：043038.DUAN Changrui，ZHENG Qun，XUE Junhua，et al. Experimental study on zonal failure discontinuous deformation of deep surrounding rock under different working conditions[J]. Journal of Mining and Strata Control Engineering，2021，3( 4 )：043038.

[20] 靖洪文，孟庆彬，朱俊福，等.深部巷道围岩松动圈稳定控制理论与技术进展[J].采矿与安全工程学报，2020，37( 3 )：429-442.JING Hongwen，MENG Qingbin，ZHU Junfu，et al. Theoretical and technical progress of stability control of broken rock zone of deep roadway surrounding rock[J]. Journal of Mining & Safety Engineering，2020，37( 3 )：429-442.

[21] PORATHUR John Loui，ROY Pijush Pal，SHEN Baotang，et al.Highwall mining：Applicability，design & safety[M]. Britain：CRC Press，65-66.