类水滴型扰流元顺排式矩形微通道的流动换热性能研究*
侯娜娜,张 东,李树谦,张 猛
(1.河北水利电力学院土木工程系,河北 沧州 061001;2.河北科技大学建筑工程学院,河北 石家庄 050018;3.河北省数据中心相变热管理技术创新中心,河北 沧州 061001;4.沧州市储热及低品位余热利用型电磁供热技术创新中心,河北 沧州 061001)
随着科技水平的提升及工业现代化的快速发展,越来越多的领域散热问题日益突出,如数据中心、电子芯片冷却、5G 基站等[1]。为解决日益突出的电子器件散热问题,国内外研究学者已开展了大量关于通过增加扰流结构或改变扰流结构形式等方法进而增强对流换热效果的研究。
CHEN 等[2]研究了宏观尺度下流动工质为空气的类水滴型顺排扰流元的矩形通道的流动换热性能,并发现在雷诺数Re变化范围为900~9000 时,水滴型扰流元结构散热性能要优于圆形扰流元结构。谭晓茗等[3]进行了宏观尺度下流动工质为空气的水滴形和圆形叉排扰流柱阵列矩形通道内流动和换热的数值模拟,发现水滴形比圆柱形扰流的强化换热效果约下降15%,但流动阻力却下降了近50%。王奉明等[4-6]对宏观尺度下不同形状扰流柱叉排阵列的矩形通道空气流动过程进行了试验和三维数值模拟,分析了扰流柱形状和来流Re数对换热特性的影响,并对其强化换热特性和压力损失特性进行了对比分析,发现水滴形扰流柱群矩形通道的综合性能最佳。
杨超、张高高等[7-8]通过数值模拟方法对微观尺度下流动工质为水的变密度凸肋通道及改变水滴型尾缘角度通道的流动和换热特性进行了研究,在Re=100~600 时,水滴型肋片换热性能优于圆形肋片并随尾翼长度增加而增强。前述调研发现,以往学者对于类水滴型扰流元换热性能的研究主要集中在宏观尺度或流动工质为空气的工况下,而对于微观尺度并且流动工质为水的工况下类水滴型扰流元的流动换热性能研究较少。为此,本文设计了类水滴型顺排式扰流结构的矩形微通道并对其流动换热性能进行了数值模拟研究。
1 物理模型
本数值模拟采用的物理模型主要分为3 个部分,即入口缓冲区域、扰流流动区域、出口缓冲区域,其长度L1、L2、L3分别为2.0 mm、15.8 mm、2.2 mm,矩形微通道总长度为20 mm,通道高度为0.2 mm,宽度为3 mm,矩形微通道厚度为0.2 mm。矩形微通道内扰流元为类水滴型,其高度与矩形微通道高度相同。通道内共5 排类水滴型扰流元,每排共16 个扰流元,且扰流元采用顺排布置方式。矩形微通道材质为铝,通道内的流体为去离子水。矩形微通道内扰流元的布置及流体流动方向如图1 所示。

图1 矩形微通道内扰流元的布置及流体流动方向
矩形微通道内类水滴型扰流元布置为对称结构,扰流元的大圆半径为0.15 mm,小圆半径为0.08 mm,两圆间距为0.50 mm。扰流元间的横向距离为0.6 mm,水流方向距离为0.5 mm(二者均为圆心间距)。相邻两排扰流元间横截面形成了渐缩渐扩流道,横截面最小间距为0.3 mm,最大间距为0.45 mm,与矩形微通道侧壁面相邻的扰流元间的流道横截面最小间距为0.15 mm,最大间距为0.23 mm。
2 数学模型
文献[8]提出了区别于常规通道的水滴型微通道内流动换热的数值模拟方法,参照其提出的数值模拟方法,认为本模型中工质为不可压缩流体,物性参数为常数不随温度变化,热辐射作用忽略不计,计算区域采用层流模型,考虑表面张力的影响,压力速度耦合采用SIMPLE 计算方法。
3 边界条件
本模拟主要研究流体入口速度改变时类水滴型顺排式微通道的换热性能,入口边界条件为给定速度及温度,出口边界条件为自由出流,矩形微通道底面为恒定热流加热壁面,速度无滑移,其他壁面均为绝热壁面。矩形微通道边界条件设置的具体内容如下:入口流体流速为0.2 m/s、0.4 m/s、0.6 m/s、0.8 m/s 和1.0 m/s,入口流体温度为300 K,加热壁面热流密度为300 kW/m2。
4 网格划分与验证
采用多面体网格对计算区域进行网格划分,在扰流元与流体接触面附近采用curvature 和proximity方式进行网格加密。网格划分示意图如图2 所示。

图2 矩形微通道的网格划分示意图
为确保数值模拟的计算时间和准确度而进行了3组数据的网格无关性验证。网格数分别389685、494890、607389。在入口流速为0.2 m/s 时,进出口温差及压降的误差分别为3.08%、1.31%和2.75%、1.53%。通过误差比较,发现网格数为494890 时较为合适。
5 数据处理
文献[8]对水滴型扰流元矩形微通道的水力直径D、对流换热系数h、雷诺数Re、努塞尔数Nu及摩擦阻力系数f等进行了较为详细的说明。本文采用矩形微通道类水滴型顺排结构进行流动传热分析,与文献[8]十分相似,故本文采用文献[8]相应公式进行数据处理。
6 结果与讨论
图3 为入口流速0.6 m/s 时矩形微通道内速度、温度及压力的分布云图。矩形微通道内流体速度整体呈现增长趋势。由入口缓冲区域进入扰流流动区域时,在扰流元通道内的流体流速有明显的增加,其主要原因在于通道横截面突然变小,形成了喷管结构,流体流动满足喷管截面变化规律,当截面突然变小时,其流速增加。

图3 矩形微通道速度、压力、温度分布云图
此外,扰流元通道内的流体速度沿流动方向逐渐增加,主要是由于相邻两排扰流元间的横截面以渐缩—渐扩—渐缩的规律进行变化,从而使得流体速度逐步叠加。随后扰流流动区域末端较高速度的流体在出口缓冲区进行较为平缓的汇合,相较于扰流流动区域流体速度有所降低。
矩形微通道内温度变化趋势与速度变化趋势相似,均沿流动方向逐渐增加。流体温度在入口缓冲区温度最低,约为302 K,在出口缓冲区温度最高,约为322 K。类水滴型扰流元温度在扰流区域第1 列温度最低,约308 K,在第14 列温度最高,约为324 K。虽然流体在流动过程中速度在逐渐增加,但流体在流动过程中不断与加热壁面进行热量交换,从而流体温度随流动不断增加。与之相对应的是在扰流流动区域末端流体带走热量的能力与起始端相比较弱,故在恒定加热壁面条件下,扰流流动区域末端扰流元温度高于起始端扰流元温度。
与图3(a)和图3(b)相比较,图3(c)中所示的不同之处在于微通道内压力是逐渐降低的,并且在入口缓冲区域及出口缓冲区域压力降低较为平缓,而在扰流流动区域压力降低较为明显。扰流区域末端压力与始端相比降低了约8 kPa,其原因主要是由于扰流元的布置及微通道长度明显长于其他两个区域,使得扰流流动区域的沿程阻力,特别是局部阻力均高于其他区域。
图4 为不同雷诺数Re下的微通道进出口压降变化趋势。由图可见,随着Re的增大,压差随之变大且基本呈线性变化,其主要原因是由于入口流速增加导致微通道内沿程阻力和进出口处局部阻力均增大所致。
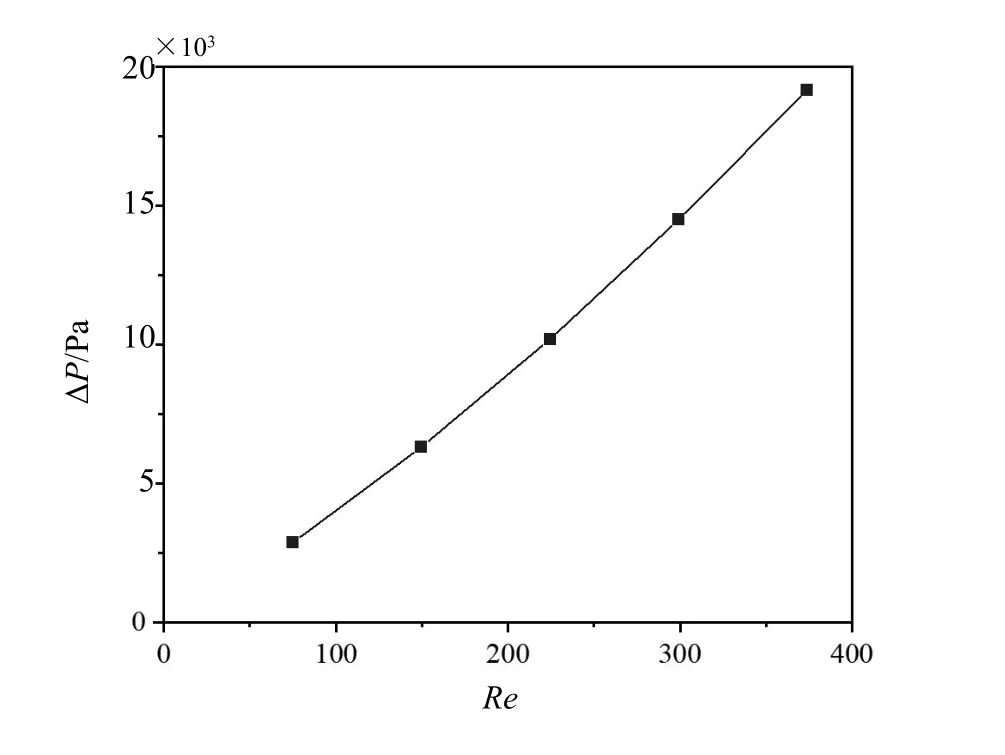
图4 微通道进出口压降随雷诺数变化情况
图5 和图6 分别为不同雷诺数Re下的平均对流换热系数和平均努塞尔数变化情况,随着雷诺数Re的增大,平均对流换热系数和平均努塞尔数均呈增加且增加趋势基本一致。由公式可以看出,微通道水力直径与导热系数为定值(假设导热系数为常数),故平均对流换热系数和平均努塞尔数变化趋势基本一致。雷诺数Re增大导致平均对流换热系数增加的主要原因可能是雷诺数Re增大会使流体流动边界层厚度和热边界层厚度减小,进而使得平均换热系数增加。

图5 平均对流换热系数随雷诺数变化情况

图6 平均努塞尔数随雷诺数变化情况
利用最小二乘法,获取了矩形微通道类水滴型扰流元顺排布置且雷诺数Re处于74~375 时,雷诺数与平均努塞尔数的关系式,即Nu=3.68289Re0.33312。
7 结论
本文考察了不同雷诺数下类水滴型扰流元顺排式矩形微通道的流动和传热特性,主要结论概括如下:①随着雷诺数Re增加,微通道内的压降、平均对流换热系数及平局努塞尔数均呈现增加趋势,且平均对流换热系数及平局努塞尔数增加趋势基本一致。其主要是由于流速增加使得进出口沿程阻力和微通道内沿程阻力增大,从而导致微通道进出口压降增大,此外雷诺数的增加导致流体流动边界层厚度和热边界层厚度减小,进而强化了换热。②定量研究发现,在入口流速范围为0.2~1.0 m/s 的情况下,矩形微通道的压降约为2.8 ~19.2 kPa,平均换热系数约为25.25 ~42.83 kW/(m2·K),平均努塞尔数约为15.78~56.77。③进一步理论分析表明,当雷诺数Re取值在74~375范围内时,雷诺数与平均努塞尔数存在以下关系,即Nu=3.68289Re0.33312。

