基于深度强化学习的自动化集装箱码头集成调度方法*

尹 星 张 煜,2 郑倩倩 唐可心▲

（1. 武汉理工大学交通与物流工程学院 武汉 430063;2. 广东省内河港航产业研究有限公司 广东 韶关 512000）

0 引 言

集装箱码头是连接海路运输的重要枢纽，其作业效率关乎港口的运营效益和码头竞争力。岸桥、水平运输工具，以及场桥是进行集装箱码头装卸船作业的重要自动化设备，对于全自动化集装箱码头而言，码头的运作效率和运作成本很大程度上由这3 种设备之间的协调性决定，因此3 种设备的资源分配与协同调度一直是集装箱码头的研究热点。

集装箱调度过程涉及多个环节，岸桥对海侧集装箱进行装卸，集卡对集装箱进行运输，场桥负责集装箱在堆场的取放作业。部分学者对单一作业环节进行研究，如高雪峰[1]对2台场桥存取混合作业模式进行了建模和求解；丁一等[2]研究自动化集装箱码头自动导引运输车（automated guided vehicle,AGV）调度问题，分析AGV路径选择和调度策略对港口装卸效率的影响；夏孟珏等[3]重点研究了岸桥故障突发情况下装卸船作业重调度策略。但集装箱码头调度是1 个联合作业过程，仅考虑单一作业环节无法实现码头整体生产的优化，一些专家侧重于从2阶段设备协同作业角度进行集装箱调度优化，比如，梁承姬等[4]对多船作业模式下岸桥和集卡协同调度问题进行研究；陈超等[5]对港口泊位分配与集卡路径规划进行研究。也有学者对岸桥、运输小车，以及场桥3阶段作业联合调度过程展开研究，如常祎妹等[6]将岸桥间、场桥间干涉和集卡速度变化等不确定性因素考虑在内，研究装卸作业模式下集装箱码头集成调度问题。

传统的求解集装箱调度的方法主要有精确算法、元启发式和启发式算法、仿真方法，Kim等[7]提出了1 种分枝界定方法来获得岸桥调度问题最优解；秦天保等[8]从约束规划角度对岸桥、集卡和场桥的集成调度进行建模，并使用CPLEX 求解器进行求解。但由于2阶段及以上的集装箱联合调度问题属于典型的NP 难组合优化问题[9]，精确算法难以在有效时间内进行求解。启发式与元启发式算法在NP 难问题求解方面有着广泛的应用，也取得了良好的效果，如钟祾充等[10]使用改进布谷鸟算法求解码头3 阶段集成调度问题；陈超等[11]提出1种双层遗传算法对岸桥、集卡和场桥3种设备数量配置。杨彩云等[12]使用Anylogic 仿真平台，对自动化码头内部智能运输机器 人（artificial intelligence robot of transportation,ART）动态调速问题进行研究，但仿真方法优化能力有限且无法直接给出调度方案。

随着人工智能的发展，一些学者开始探索使用强化学习方法来解决港口调度问题。强化学习是1种具有自主决策能力的机器学习方法[13]，与环境交互为目标，从智能体自身经验中进行学习，更加适用于复杂的动态环境。目前在港口调度领域使用较为广泛的强化学习算法主要有Q-Learning、deep Q-network（DQN）和Actor-Critic 算法。张华胜[14]将Actor-Critic 深度强化学习与启发式算法进行结合，设计算法框架，对自动化跨运车和场桥集成作业过程进行优化；尚晶等[15]提出了基于Q-Learning 算法的集卡调度强化学习模型，仿真结果显示该算法能够对集卡调度策略进行明显优化。Q-Learning 是1 种基于表格型的方法，面对大规模调度环境时，庞大的动作空间会导致“维数灾难”问题，为了解决这个问题，DQN 引入神经网络来拟合Q 值[16]，文献[1]使用改进搜索策略和采样方法的DQN 算法来解决自动化堆场双场桥协同调度问题。

综上，集装箱装卸作业是1 个多环节的联合调度问题，使用简单启发式和静态优化方法对码头3阶段调度问题求解易陷入局部最优，且算法搜索时间较长。强化学习能够实现与动态调度环境的自主交互，且目前已有一些学者将强化学习成功应用于码头实际调度过程，但研究侧重于单一作业环节，缺乏对自动化集装箱码头多环节联合调度问题的研究。

因此建立岸桥、ART，以及场桥的3 阶段集成调度模型，更有利于从整体优化集装箱调度过程，降低港口运作成本。针对集装箱卸船作业的特点，以车间调度领域的混合流水车间理论[17]为基础，以最小化总完工时间为目标，建立自动化码头集装箱3 阶段混合流水车间集成调度模型。考虑到集成调度问题的离散性和调度环境实时性、动态性的特点，设计贴合码头实际调度环境的深度强化学习算法（double deep Q-network，DDQN）进行求解。

1 问题描述与模型构建

1.1 集成调度问题

天津港C 段自动化集装箱码头前沿布局见图1。卸船作业流程为：船舶靠岸后，单小车岸桥移动到指定贝位，将集装箱从船上抓起后卸载到ART上，然后由ART运送该集装箱至堆场指定场区，由双悬臂场桥将集装箱从ART卸下放置于堆场指定位置。集装箱装船作业可以看作是上述操作的反向过程。

图1 码头前沿布局示意图Fig.1 Layout diagram of wharf front

集装箱卸船作业可以被模拟为工件在流水线上加工的过程。见图2，将n个集装箱视为不同的工件，依次通过岸桥、ART，以及场桥这3 个阶段的设备处理，完成卸船作业，且每个集装箱对每个阶段的设备均只经历1 次，同一阶段的设备属于并行机。因此，本文将运用混合流水车间原理及其方法来建立自动化集装箱码头卸货过程中岸桥、ART，以及场桥3个阶段的集成调度模型。

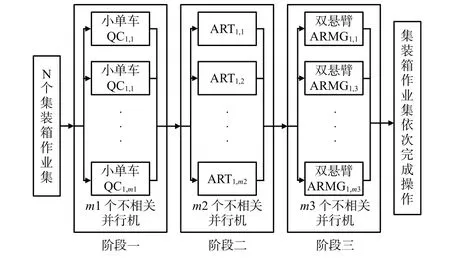
图2 集装箱卸货过程3阶段流水车间调度示意图Fig.2 Schematic diagram of three-stage flow shop scheduling about container unloading process

1.2 集成调度模型

考虑集装箱港口调度过程中存在许多实际约束条件，因此需要在传统混合流水车间调度问题中加入额外设备作业约束。描述如下：①船上处于同一位置（行号和列号相同）的集装箱之间存在作业顺序制约，上层集装箱优先作业；②ART运送集装箱到达堆场时需在相应位置等待，直至有完成上1 个装卸任务的岸桥出现，ART才能释放集装箱。

考虑到多设备集成调度的复杂性，将实际场景简化，对模型做如下假设。

1）集装箱都是同一类型标准箱。

2）将处于同一贝位中、作业类型相同（在堆场摆放于同一箱区）的集装箱划分为1个作业集，岸桥在对某1个作业集操作完成之前，不会移动到下1个作业集。

3）由于各阶段设备的准备时间较长，比如岸桥和场桥的移动时间等，所以计算总完工时间时考虑设备准备时间。

4）不考虑设备故障等突发情况。

5）不考虑翻、倒箱时间。

6）集装箱转移到堆场的目的位置是已知的，且同一作业集的集装箱运送到堆场同1个箱区。

模型参数定义及说明见表1。

表1 3 阶段混合流水车间调度模型参数及说明Tab.1 Parameters and description of three-stage hybrid flow shop scheduling model

目标函数为

约束条件为

以下为决策变量取值区间。

式（1）为目标函数，表示最小化最大完工时间；式（2）为各阶段设备选取虚拟作业集O作为起始作业集；式（3）为各阶段设备选取虚拟作业集V作为终止作业集；式（4）为每个阶段、每个作业集有且仅有1台设备操作它；式（5）为作业集先后作业顺序，也就是各阶段设备的作业序列；式（6）为每1个正在被服务的作业集有且仅有1 个作业集在其之前和之后；式（7）为阶段1 中的作业集由优先级Φ约束；式（8）为前后2 阶段中，作业集i开始被服务的时间关系；式（9）为各阶段中每台设备最早可开始工作时间；式（10）为各阶段中每个任务的结束时间；式（11）为同1个作业集在前后2 个阶段中的作业时间约束；式（12）为在同一阶段中，作业集i开始被操作的时间小于/等于其结束被操作的时间；式（13）和式（14）为若同一阶段k中，先后2个作业集i和j分配给同一设备m操作，则操作时间要错开相应的准备时间；式（15）和式（16）为决策变量的取值。

2 基于深度强化学习的调度算法设计

2.1 深度强化学习算法简介

在自动化集装箱码头装卸系统中，将岸桥作业系统、ART 水平作业系统和场桥作业系统看作3 阶段智能体决策系统，将集装箱调度过程使用强化学习进行描述，见图3。智能体采取动作作用于码头集成调度环境，然后转移到下1个状态，环境给出即时奖励，如此循环往复，最终由各阶段设备确定的集装箱任务操作序列便是最佳调度方案。

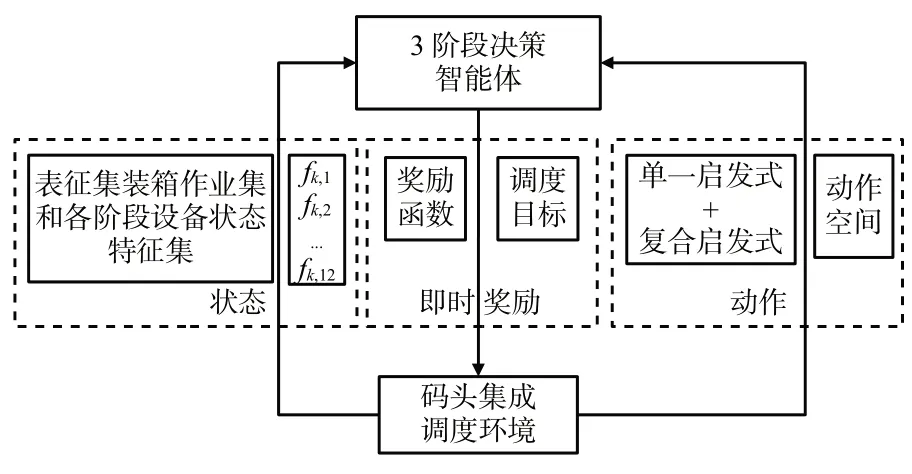
图3 基于深度强化学习的集装箱集成调度机制Fig.3 Container integrated scheduling mechanism based on deep reinforcement learning

2.2 马尔科夫决策模型构建

马尔科夫决策过程（Markov decision processes,MDP）是强化学习问题理想化的数学表达形式[18]，前文所述的自动化集装箱码头3阶段调度问题可转化为1 个马尔科夫决策过程，对马尔科夫决策过程的状态空间、动作空间、奖励函数做出如下定义。

2.2.1 状态空间设计

状态特征和动作空间的设计与调度问题密切相关，一般需要遵循以下原则：①状态特征要有代表性，能够描述码头调度环境的主要特点和变化；②状态特征是对设备状态变化的数值表示，可以用相对统一的尺度描述，并且易于计算。

结合码头实际作业情况，将阶段k中的设备Mk的第h个特征记为fk,h，为各阶段设备定义不同的特征值，包括反映码头整体调度环境变化的全局特征和反映设备特点的局部特征：为阶段1 的设备定义8个特征（1 ≤h≤8），对于阶段2的设备定义10个特征（1 ≤h≤10），对于阶段3 的设备定义10 个特征（1 ≤h≤8,h=11,12）。

状态特征具体定义如下。

式中：Ωk={1,2,···,}为当前在设备Mk排队的集装箱作业集集合，绝对值表示数量。该状态特征描述各阶段设备上集装箱的数量分布。

该状态特征表示当前分配在各阶段设备上的平均工作负载。

式（19）和（20）为在各设备上等待的集装箱作业集最长/最短操作时间。

式（21）和（22）为队列Ωk中等待的作业集中剩余最长/最短操作时间的归一化表示。

式中：为正在设备上加工的集装箱作业集的剩余操作时间，为作业集在该设备上的已加工时间。若fk,7=0，则表示该阶段设备空闲。

式（24）为即使在有作业集等待加工的情况下，是否让当前设备保持空闲（比如岸桥作业区域划分）。

式（25）为ART 是否可以采取Johnson 启发式规则1定义的动作。

式（26）为ART 是否可以采取Johnson 启发式规则2定义的动作。

式（25）和式（26）中：Q1和Q2为将船上的集装箱作业集按照作业时间进行划分，Q1为在堆场作业时间大于岸桥作业时间的作业集，其余作业集划分为Q2。

式中：trat,2为ART 到达堆场的剩余时间；twait,3为场桥发生干涉时ART 的等待时间。按照ART 预计达到堆场指定位置的剩余时间和ARMG 发生干涉时ART 的等待时间，将当前队列分为A1和A2，A1表示等待时间大于剩余达到时间的作业集集合，其余划分到A2。该状态特征决定ARMG是否可以采取Johnson启发式规则3定义的动作。

式（28）为ARMG 是否可以采取Johnson 启发式规则4定义的动作。

2.2.2 动作空间设计

动作空间就是智能体在当前状态下可以采取的动作候选集合，在码头集成调度问题中，智能体执行的动作是依据调度规则优先选择要操作的集装箱作业集。启发式调度规则时间复杂度较低，但混合调度规则比单一调度规则的求解效果好[19]，且目前已有一些将混合启发式调度规则应用于强化学习算法中，并在车间调度问题与资源投入调度领域取得了良好的效果[20-24]。因此本文选择了5 条被广泛使用的单一调度规则，并在此基础上结合码头实际作业情况，为ART 阶段和场桥阶段增添了复合调度规则，见表2。因此，单小车岸桥能够采用的行为集合是，ART 能 够 采 用 的 行 为 集 合 是，场桥能够采用的行为集合是

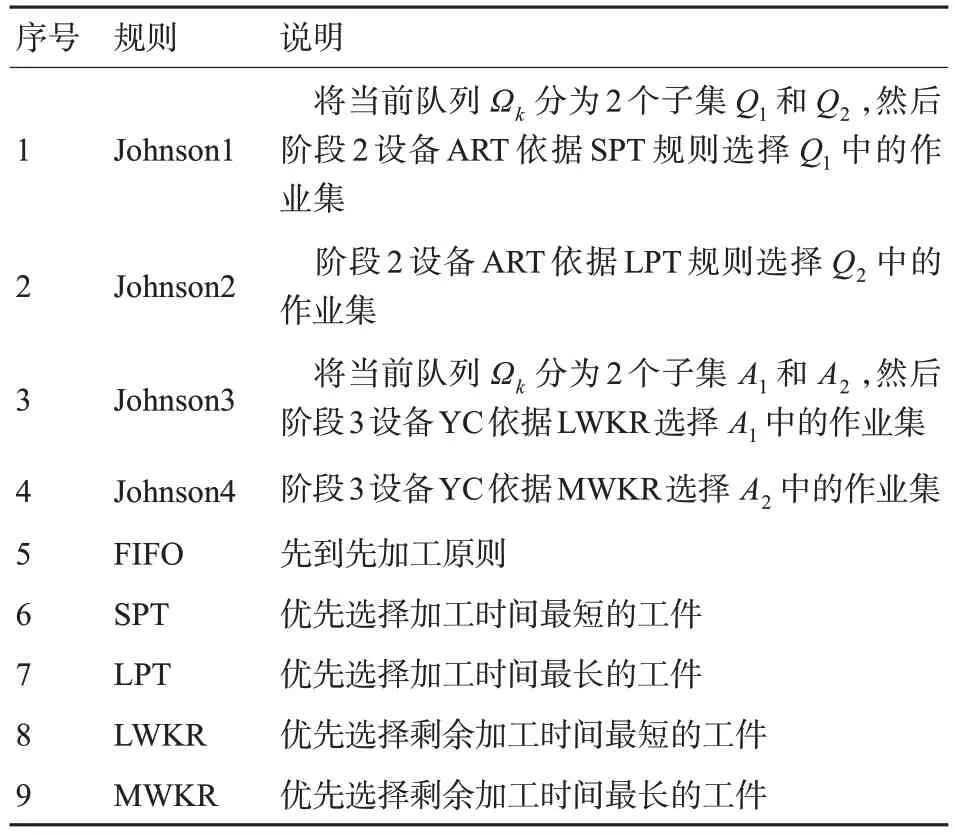
表2 调度规则Tab.2 Scheduling rules

2.2.3 奖励函数设计

奖励函数定义适当与否与调度效果密切相关，本文的调度目标为式（1），即最小化最大卸船作业完工时间，这一目标可通过最大化加工设备利用率来进行转换。对于集装箱码头来说，提高各阶段设备的利用率是提升码头整体装卸效率的关键，因此使用平均设备利用率来表示调度目标。借鉴文献[20]中的表达方式，将平均设备利用率表示为集装箱作业集在各阶段设备上的总操作时间与整体最大完工时间之比，数值表示具体如下。

式中：Si,m,k为集装箱作业集i在阶段k中对应设备m上的开始操作时间；Ei,m,k为集装箱作业集i在阶段k中对应设备m上的终止操作时间；Mk为阶段k中设备数量。

由式（30）可见：设备利用率与最大完工时间为反比关系，设备利用率越高，最大完工时间越小。

2.3 算法流程

Q-Learning 采用Q 表来存储状态集合，进而通过更新动作-值函数Qπ( )s,a来进行动作选择。但调度环境的状态集合规模大，大量的状态-行为信息超过了Q 表的存储容量，从而导致“维数灾难”问题。为了解决这个问题，DDQN（double DQN）算法采用带参数的神经网络来近似拟合动作-值函数Qπ(s,a|θ)[21]。同时为了避免过估计（over estimation），算法使用双网络模式，将动作选择（当前Q网络）与动作评估（目标Q 网络）分离开，并引入经验回放机制打破数据之间的相关性，使神经网络训练过程更加稳健。神经网络的输入层为每台设备对应的状态特征；之后连接4 个全连接层，激活函数使用relu 函数；输出层为对应输入状态的动作预测value值。

DDQN 算法中的目标Q 网络的参数（θQ）是隔一段时间从当前Q 网络（θQ′）中复制而来，2 个Q 网络的结构相同。设定n步之后，采用软更新（soft-update）的方式来更新。

式中：τ为更新系数，一般取值较小，比如取值0.1或0.01。

多智能体DDQN算法流程见图4。

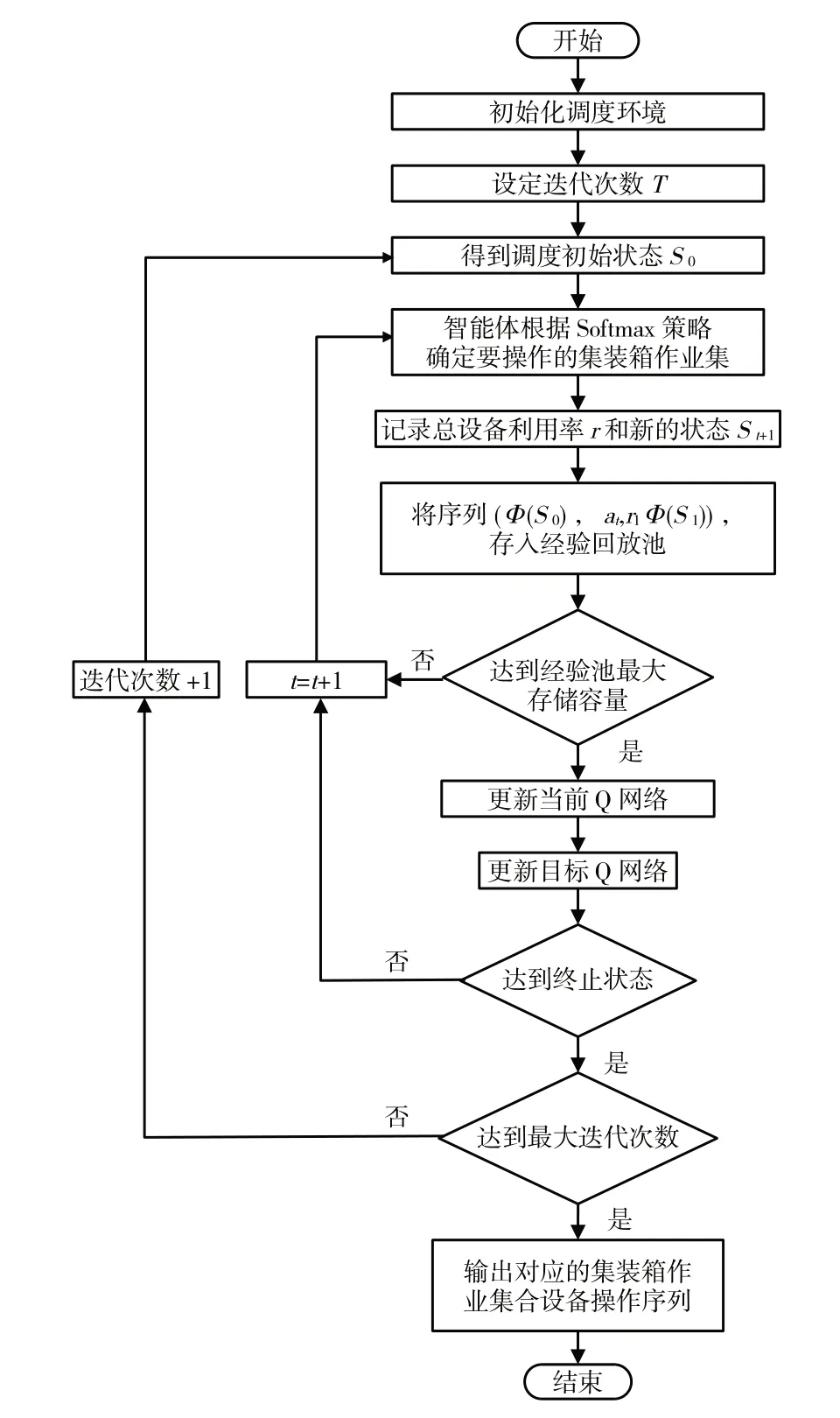
图4 调度算法流程图Fig.4 Flow chart of scheduling algorithm

3 算例分析

3.1 各阶段设备参数

为了验证所提出模型和算法的有效性和可行性，根据天津港实际调研情况设计实验算例。天津港C段码头采用单小车岸桥-ART-双悬臂场桥的装卸工艺，每台岸桥1 次可吊起1 个FEU 或2 个TEU，每辆ART 1次可运载1个FEU或2个TEU，堆场一共有8 个箱区，每台场桥1 次可装卸1 个FEU 或2 个TEU。各设备作业时间见表3。

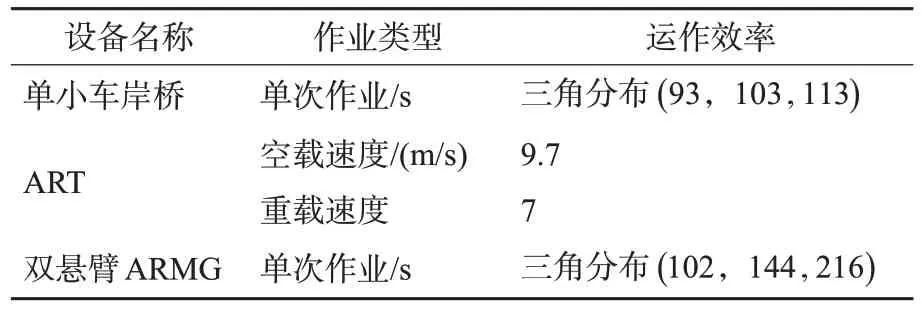
表3 集装箱码头各阶段设备运作效率Tab.3 Operation time of equipment at each stage of container terminal

表4为码头前沿与堆场各箱区之间的距离。

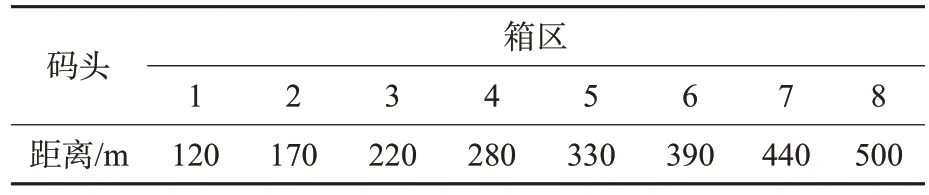
表4 码头前沿距各箱区的距离Tab.4 Distance from wharf apron to each container area

3.2 DDQN算法训练与求解

依据3.1节自动化码头相关参数，以1个规模为300 个集装箱的算例进行验证。假设300 个集装箱分布在同1 艘船舶的15 个贝位中，每个贝位包含20个集装箱，分为2 个作业集，则一共有30 个作业集，配套使用4台岸桥、15辆ART和8台场桥（每个箱区1台）进行卸船作业，设定ART在岸桥和场桥下的停留时间均为20 s。

调度算法采用Python3.7 语言实现，在Tensor-Flow2.0 框架中实现，运行于Windows11 64 位操作系统，处理器为Intel Corei5-9400 CPU2.90GHz，RAM 为8GB 的PC 机。调度环境使用OpenAI 的Gym搭建。参数的设置对算法的训练时间和求解质量有着重要影响，按照一般设置原则[24]，深度强化学习调度算法参数设置见表5。

表5 算法参数设置Tab.5 Algorithm parameter setting

算法收敛曲线见图5。由图5可见：随着迭代次数的增加，算法能够使调度目标以较快的速度减少，约1 200代时达到较优结果并收敛。

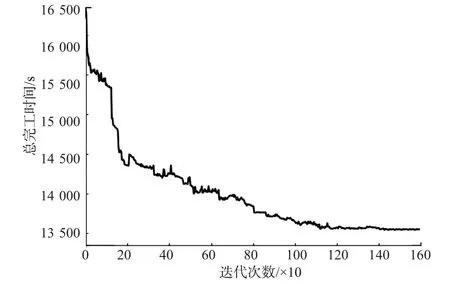
图5 算法收敛图Fig.5 Algorithm convergence graph

深度强化学习算法调度结果见图6。

图6 调度结果甘特图Fig.6 Gantt chart of dispatching results

单小车岸桥调度方案见表6，ART 指派结果见表7，双悬臂场桥调度方案见表8。

表6 单小车岸桥调度方案Tab.6 Single trolley quay crane dispatching scheme

表7 ART 指派结果Tab.7 Art assignment results

表8 双悬臂场桥调度方案Tab.8 Double cantilever yard crane dispatching scheme

由调度结果可知，3 阶段设备总作业时间为13 550 s，其中第1阶段4台岸桥利用率很高，负荷较为均匀，第2阶段ART平均利用率为98%，负荷较为均衡，第3阶段场桥平均利用率为71%，最低负荷率为54%，最高为84%，说明ART的配置数量能够满足岸桥作业速度，减少了岸桥等待时间。实际作业中，天津港C段自动化码头目标效率（90% TEU） 为每小时489 箱（平均每台岸桥不低于27 TEU/h），DDQN算法每台岸桥作业效率为34 TEU/h，说明调度结果能够满足实际应用要求。

4 模型验证

4.1 与精确算法求解比较

为了验证所提算法的有效性和模型的正确性，设计10 个小规模算例，并将Gurobi 求解结果和深度强化学习算法求解结果进行对比，对比结果见表9。表9 中n×Q×A×M为所设计案例的规模，即集装箱作业数×单小车岸桥数量×ART 数量×双悬臂场桥数量；e1，e2分别为Gurobi 和深度强化学习算法的求解结果；t1，t2分别为Gurobi 和深度强化学习算法对算例的求解时间为深度强化学习算法求解结果对Gurobi求解结果的相对误差。

由表9 的小规模案例求解对比结果可见：所提出的深度强化学习算法在多数情况下能够得到与Gurobi 非常接近的最优解，平均求解误差为1.99%。但随着案例规模逐渐增加，Gurobi 求解器的计算时间显著偏高，说明所提出DDQN 算法在求解较大规模算例时具有一定时间优势。

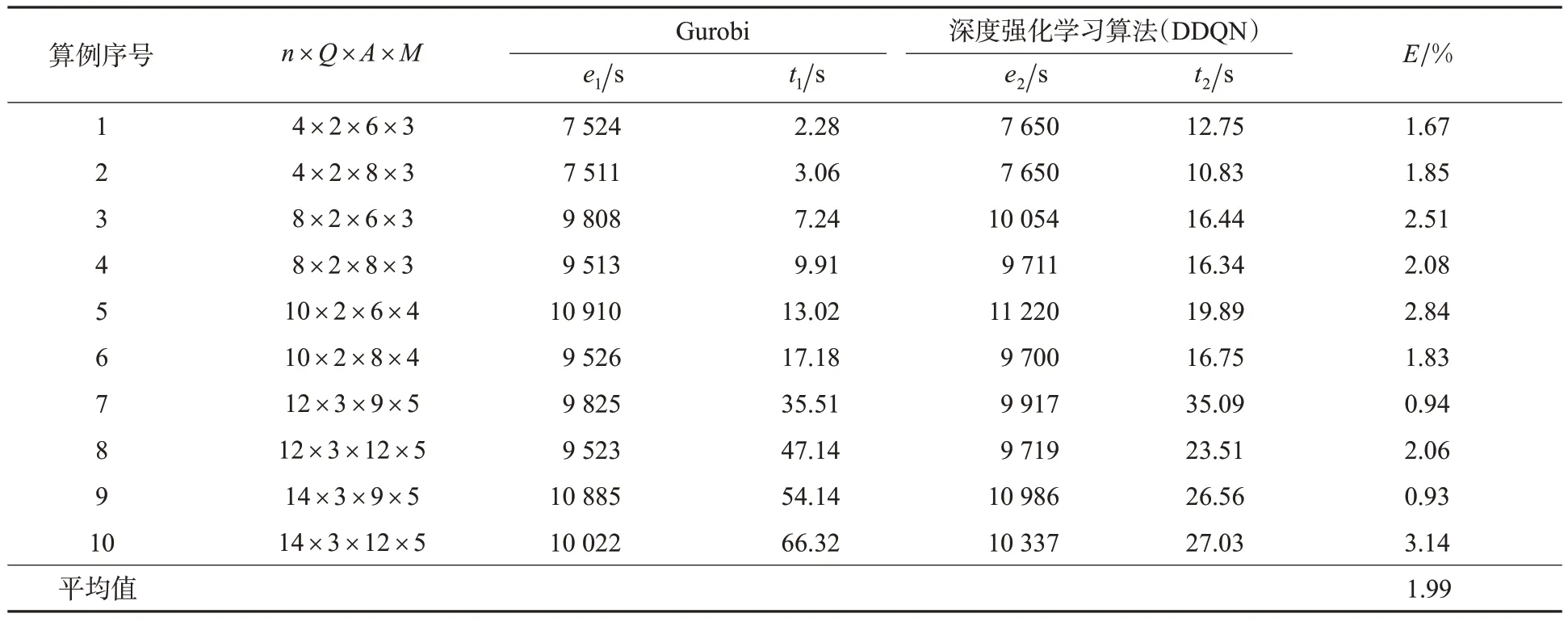
表9 小规模算例下Gurobi 和深度强化学习算法求解结果对比Tab.9 Comparison of solution results between gurobi and deep reinforcement learning algorithms for small-scale examples

4.2 与单一调度规则求解比较

为进一步验证算法的优越性，对天津港C段3艘船舶的集装箱进行验证，由于Gurobi在表10设置的3种大规模的实例环境（集装箱作业数×单小车岸桥数量×ART数量×双悬臂场桥数量）下无法实现精确求解，因此对DDQN 算法和使用5 种单一调度规则的策略、粒子群算法（particle swarm optimization,PSO）进行性能测试，每个实例进行10次仿真实验并取平均值记录，测试结果见表10。表10中所用的粒子群算法采用文献[25]推荐的参数，惯性权重ω=0.729，加速因子c1=c2=1.494 45。

表10 较大规模算例求解对比Tab.10 Comparison of large-scale numerical examples

由表10可见：随着集装箱任务数量和设备数量的增多，DDQN算法的求解效果均好于单一调度规则与粒子群算法，显现出一定的优越性，3 个算例中DDQN 与下界值的差距分别为6.0%，5.6%，4.6%。特别说明的是，强化学习算法训练需要耗费时间较长，但训练好的算法能够在20 s 内得到最优结果。

为进一步验证算法稳定性，对算例60×12×26×14 分别进行100次求解，得到求解结果与理论下界差距箱型图，见图7。从图7 可见：相对于使用单一启发式调度规则，DDQN 算法与理论下界值差距的下限和中位数小，且数据分布较为集中，无明显异常值。表明DDQN 算法具有较好的稳定性，且具有明显的求解优势。

图7 6种策略与理论下界值差距箱型图Fig.7 Box plot of the gap between six strategies and the theoretical lower bound

为分析所使用的启发式调度规则在深度强化学习算法中的作用，统计求解所有实验算例过程中9种启发式动作的使用频率，见图8。由图8 可见：使用频次较 多的为Johnson1 和Johnson2，Johnson3 和Johnson4，SPT，LPT，MWKR，说明这些规则对产生最优调度结果贡献较大，而FIFO和LWKR使用频次较少，效果不太突出，后续可以考虑增添其他启发式行为进行替换。

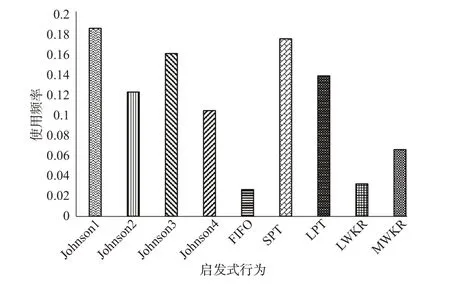
图8 启发式行为使用频率统计Fig.8 Heuristic behavior usage frequency statistics

5 结束语

针对集装箱码头卸船过程中岸桥、ART 和场桥设备的集成调度问题，建立了以混合流水车间为基础的3 阶段混合整数规划模型，以天津港C段自动化码头实际调研数据为基础，设计不同规模算例进行求解，通过与Gurobi 求解结果对比，验证了模型和算法的有效性；为进一步验证复合调度规则的优越性，对比7 种算法的求解方案，结果表明所提DDQN 算法更具优势，求解的完工时间更接近理论下界值。此外，由于每个港口的操作工艺不同，因此针对不同港口需要对模型和算法的细节进行调整，后续会进一步考虑算法在其他港口集成调度问题适用性。