赤道大洋驻波异常及其年际变化的理论分析

卢姁，赵艳玲，张东凌，张铭，刘赛赛

(1.中国人民解放军32021 部队，北京 100094；2.中国人民解放军31010 部队，北京 100081；3.中国科学院大气物理研究所，北京 100029；4.国防科技大学 气象海洋学院 大气环流与短期气候预测实验室，江苏 南京 211101)

1 引言

最早研究赤道波系的是Matsuno，由于赤道上Coriolis 参数f为0，但它的导数 β=df/dy在该处又最大，从而使得赤道海域的波动成为海洋动力学中最具有特色的运动[1]。从波动在海洋的传播看，在赤道海洋，向东传播的有开尔文波，向西传播的有罗斯贝波，此外还有高频的惯性重力波以及特殊的混合罗斯贝重力波，这些构成赤道波系。由赤道波系中的开尔文波和罗斯贝波的调节，可以产生年际变化，并是解释厄尔尼诺−南方涛动（ENSO）循环的一种机制[2]。因此人们逐渐认识到热带大洋中波动的重要性。

Kelvin 首先发现在海洋中有与岸线平行传播而波形只在岸线附近明显的波，后来人们就称之为开尔文波。显然该岸线的束缚是重要因子。当f随空间变化时，Matsuno[1]发现，即使没有该岸线约束，也有类似的波动存在，波形只在赤道附近明显，但仅有东传的一支，在此赤道扮演了海岸线的角色。Hirst[3]、Yamagata 和Masumoto[4]从理论上证明了热带海气耦合系统中存在向东传播的扰动，并认为这是由于东传的赤道开尔文波所引起的。卢姁和张东凌[5]发现，在长江中下游地区的丰（枯）梅年，热带太平洋次表层海温异常传播路径都是沿赤道温跃层由西向东传播的，而这有可能与热带太平洋上东传的开尔文波有关。

然而热带太平洋有海岸线，向东传播的开尔文波并不能一直这样传播下去，必然会受到海洋东边界的阻挡而被反射，并有人用此来解释ENSO 现象[2]。这表明从数学物理上考虑，热带大洋的开尔文波不能满足赤道有界海洋的侧边界条件，其不是该有界海洋的一个解。此时要在赤道满足该侧边界条件的解则只能是海洋驻波或波包。

有关海洋驻波研究方面，吕新刚等[6]建立了胶州湾潮汐潮流数值模拟及预报的模型，并与实测资料做了对比，发现胶州湾内的潮波以驻波为主。李希彬等[7]依据罗源湾可门水道的25 h 连续走航观测资料，发现该水道内的潮流为正规半日潮，驻波性质明显。王春阳等[8]基于2017 年春季和冬季的海流资料分析了广东红海湾海域的潮流状况，发现该海域的潮波介于驻波与前进波之间。Zheng 等[9]利用巡航观测、卫星高度计数据和理论分析来处理南海的驻波或假潮事件，在2007 年夏季和2009 年，巡航观测到了南海海盆中的内振荡信号，信号平均波长为320 km 和390 km，最大振幅为50～100 m，出现水深在500～700 m，最大水深可达1 700 m；卫星高度计图像及理论分析表明，观测到的内振荡属二维假潮模，其至少持续了2 周，并可在东西长1 000 km，南北宽800 km，水深均匀的海盆假潮模型中获得；统计分析还表明，从1993年至2012 年中，共有94 个假潮事件。Navas-Montilla等[10]指出，稳定的浅水流通过半封闭海域的出口时，会激发出重力驻波特征模即假潮，他们对此现象做了实验和数值研究。假潮与海洋驻波类似，也有波腹和波节。以上对海洋驻波和假潮的研究表明，其多发生在封闭和半封闭的海湾和海盆中，水平尺度通常在几十千米到几百千米。目前尚未见到宽广大洋（如太平洋）中的驻波或假潮研究，而开展这方面研究是必要的。

地球上的热带大洋无论是太平洋、印度洋还是大西洋，均是有侧边界的。故而实际赤道上满足该侧边界条件的驻波和波包是否存在，若存在其空间结构和振荡频率如何，其与气候变化有何联系，这些均是物理海洋学和气候学中的重要问题。在文献[11]中，我们得到了有界热带大洋的波包解析解并用以解释热带太平洋及印度洋中流场异常复EOF 分析的结果，并对热带大洋流场异常的年际和年代际变化以及该波包解与ENSO 及印度洋偶极子（IOD）的关系做了讨论[12–14]。不过，用该波包解（前者）却不能解释卢姁等[15]得到的春季（4 月份）热带太平洋流场异常复EOF 分析第一模态（后者）的结果；后者的空间场呈现向赤道两侧迅速衰减全大洋一致的纬向流，用该第一模态实时间系数做的小波全谱图上则以6 a 的年际变化最显著，参见文献[15]中的图1b 和图4b；这样若用前者模态1（l=1）来解释，两者空间分布相一致，但前者振荡周期为12.2 a，与后者6 a 年际变化相差太远；若用前者模态2（l=2）来解释，虽两者时间变化均约6 a，但空间分布后者为全大洋一致的纬向流，而前者与此相差较大。那么在热带大洋是否存在可解释以上后者的驻波解呢？这是令人感兴趣的问题。上面分析也启示我们，后者可能与赤道驻波密切有关，某些情况下赤道驻波对热带大洋流场异常会起重要作用。

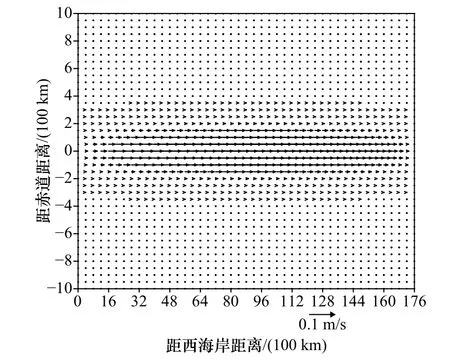
图1 t=0.25T1，n=1 时流场异常的分布Fig.1 Anomalous current distribution at t=0.25T1,n=1

为回答以上问题，并证实上面推断，本文采用一个理想热带大洋模型，在考虑该大洋东、西海岸侧边界条件后，对赤道驻波做了解析求解，以便了解其形态和特点，并对该驻波解与热带大洋流场异常的年际变化，以及其与ENSO 和IOD 之间的关系做了讨论。

2 数学模型和求解

本文在实数域中讨论，计算中采用 m ·kg·s 制。这里设大洋在垂直方向分为均质的上、下两层，这两层以跃层为界，这两层密度分别为常数 ρ1、ρ2，在引入约化重力加速度，不考虑外强迫和摩擦，也不考虑背景流后，则上层海水的控制方程满足以下赤道 β平面近似下的线性化正压扰动方程组[11]：

考虑到大洋在x=0和x=L处分别有南北向的西、东海岸，故而u必须满足以下刚壁边界条件：

在此L为热带大洋东西方向的宽度，x为赤道上距西海岸的距离。

下面来求式（1）至式（3）满足边界条件（4）的解析解。为此设u、Φ和v有如下形式：

在此取常数 δ>0，即扰动从赤道向两极地衰减，而U0、H0设为常数，可视为u、Φ在y=0处的振幅。将式（5）代入式（1）至式（3），可得以下方程组：

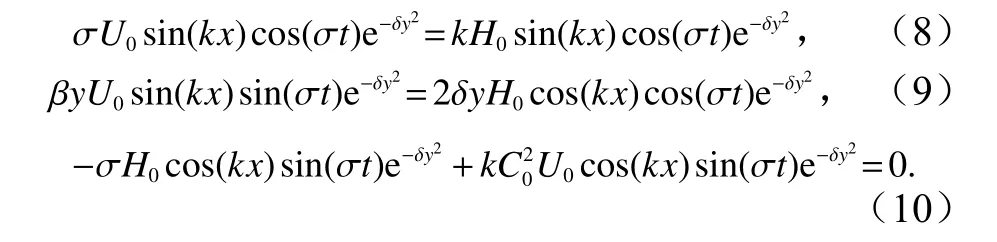
现考察式（9），当U0、H0给定后，式（9）等号两端的表达式均有界；在赤道上因有y=0，故式（9）显然严格成立；在离赤道有些距离处，因ye−δy2→0，式（9）也成立。再考虑到正、余弦函数的绝对值不超过1，及式（9）中的 β=2.289×10−11m−1·s−1其值非常小，而 δ是要待确定的系数。在做了这些考虑后，若确定后的 δ值也非常小，使得式（9）中等号两端项的量级均非常小，接近于0，则可认为在整个热带地区式（9）近似成立（含严格成立，以下均做此理解）。如此式（2）也近似成立。式（5）就是式（1）至式（3）的近似解析解。注意到正、余弦函数的绝对值不超过1，则由式（9）可得

由式（11）知，参数 δ可按以下等式来确定

由式（8）、式（10）可得

此时关于u的边界条件式（4）可写为

要满足以上边界条件则显然要有

在此正整数n称为模态数或模态序号，本文将n=1，2，···的赤道驻波扰动（异常）分别称为模态1、模态2 等，以避免与我们在流场异常复EOF 分析中的模态[15−16]称呼（第一模态、第二模态等）相混淆。

式（13）与式（14）必须要两式相容，由此两式可得U0=kH0/σ，U0=σH0/()，如此就必须要有k/σ=σ/()，从而可得k2=σ2/，再开方并考虑到式（16）后有

由式（17）可见，频率 σ与模态数n有关，模态数n越大，频率 σ就越高。同理，式（12）也可通过与式（13）相容来确定δ，采用以上相同方法可得

由式（18）中确定的 δ表达式与经典赤道开尔文波解中的相同。现取C0=0.183 m/s（文献[11]中的取值），则有 δ=6.26×10−11m−2，其值也非常小；这表明式（9）确实近似成立（该近似的精度后文4.1 节中还要详论）。如此近似满足式（1）至式（3）以及边条件（15）的u、Φ为

根据式（14）和式（17）可得H0=C0U0。再令Tn=2π/σ=2L/(nC0)，这里Tn为 模态n的周期，则式（19）、式（20）可写为

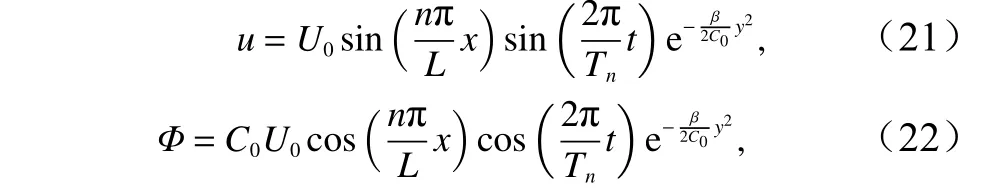
此外还有

这样式（21）至式（23）即为正压赤道驻波异常各模态的近似解析解。

3 计算结果分析

3.1 热带太平洋的结果

以下给出相应热带太平洋的计算结果。热带太平洋东西经度相距约160°。取L=17 600 km[11]；取上层海水的标准深度也可认为是热带大洋次表层的标准深度；取（ρ2−ρ1）/ρ2为 1 .704×10−5，重力加速度g=9.8 m/s2，则约化重力加速度g′=1.67×10−4m/s2，并有=0 .183 m/s；再取赤道上β=2.289×10−11m−1·s−1，δ=β/(2C0)=6.26×10−11m−2。以上参数均由环境决定，且与文献[11]中取得相同。再取U0=0.1 m/s并取不同的n值，这样由式（11）就能得到热带太平洋赤道驻波异常的情况。

对n=1，由式（8）知该赤道驻波异常的频率为σ=3.262×10−8s−1，相应的周期T1=2π/σ=6.10 a。图1 给出了t=T1/4时该赤道驻波流场异常的情况。图中横坐标向东为正，纵坐标向北为正，后同。在整个大洋范围流场异常只有半波，其经向流异常为0，纬向流异常为全大洋一致的东向流。流场异常在热带大洋中部即x=L/2处最大，向赤道南北两侧则迅速衰减，并被限制在赤道两侧约2º的范围内，其赤道俘获波的特征十分明晰。在大洋东、西海岸处，流场异常为0，满足上述边界条件，且该两处为驻点。图2 给出了t=0时该赤道驻波位势场异常的情况。位势场异常分别在赤道的东、西海岸处有最大正值、最小负值，在此两处振幅最大，并向赤道南北两侧迅速衰减。位势场异常同样被限制在赤道两侧约2º的范围内，这点与流场异常相同。大洋中部的x=L/2处则为驻点。位势场异常在整个大洋也呈半波分布。

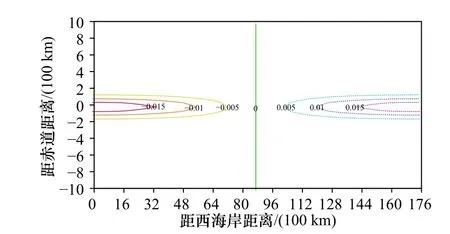
图2 t=0，n=1 时位势场异常（单位：m2/s2）的分布Fig.2 Anomalous potential field (unit:m2/s2) distribution at t=0,n=1

对n=2，该赤道驻波异常的频率为σ=6.525×10−8s−1，相 应 的周期T2=3.05 a，其周期为T1的 一 半。图3 给出了t=T2/4时该赤道驻波的流场异常情况。此时在整个大洋范围流场异常呈现1 波形态，其经向流异常仍为0，纬向流异常在大洋东部为西向流，西部为东向流。流场异常也向赤道南北两侧迅速衰减，赤道俘获波的特征也十分明晰。在大洋半宽x=L/2处以及大洋东、西海岸上，流场扰动都为0，该3 处为驻点。图4 给出了t=0 时n=2赤道驻波的位势场异常情况。整个大洋中也呈1 波分布态势；在大洋东、西部x=0至x=L/4 以 及x=3L/4至x=L区段，位势场异常为正，且在大洋东、西边界的赤道上振幅最大；在大洋中部x=L/4至x=3L/4区段该异常为负，且在热带大洋中部x=L/2处振幅最大。在热带大洋东、西边界以及x=L/2处的最大振幅也向赤道南北两侧作与流场异常类似的迅速衰减。注意参数 δ 与n无关，故在此n=2 的流场和位势场异常的衰减程度分别与以上n=1的情况相同。

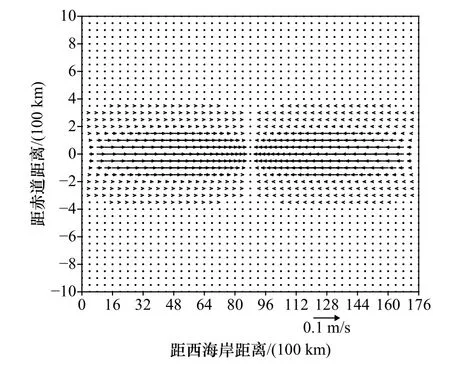
图3 t=0.25T2，n=2 时流场异常的分布Fig.3 Anomalous current distribution at t=0.25T2,n=2

图4 t=0，n=2 时位势场异常（单位：m2/s2）的分布Fig.4 Anomalous potential field (unit:m2/s2) distribution at t=0,n=2

3.2 热带印度洋和大西洋的结果

首先给出相应热带印度洋的计算结果。热带印度洋东西经度相距约70°，可取L=7 700 km[11]。除L和n外，其他参数、g′、C0和 β也均取得与热带太平洋的相 同，故 而 δ也 相 同。U0仍 取0.1 m/s。这 样 在t=T2/4时 取n=1和n=2得到的流场异常和位势场异常分别与图1、图2 和图3、图4 形态相同，这样只需将该4 张图的横坐标标定为0～77（×100 km），就可得到热带印度洋的相应图像，故此图略。两者不同之处仅在于热带大洋宽度不同，两者驻波异常的频率 σ不同，从而周期也不同。当取热带印度洋n为1 和2 时，相应的周期分别为2.67 a 和1.33 a。

接着给出热带大西洋的结果。热带大西洋东西经度相距约45°，约合4 950 km，可取L=5 000 km[11]。与热带印度洋同理，此时只需将图1 至图4 的横坐标标定为0～50（×100 km）就能得到相应的图像（图略）。此时取n为1 和2 时，其相应的周期分别为1.73 a和0.87 a。

4 有关驻波解的讨论

4.1 驻波解的近似精度

将式（5）、式（6）代入式（2）后可得式（9），这样该解满足式（2）的问题就转化为满足式（9）的问题。式（9）还可写为

式中，ε本应恒为0，这表示该方程严格成立。若该方程近似成立时，则 |ε|值就反映了本文近似解的误差大小，即该近似解的精度。由式（19）知 β=2δC0，将其代入式（24）后可得

式中给出了可能出现的极大误差 |ε|max沿 经向（y方向）的分布。为此对上述给定的δ、C0、U0值做了计算，图5a给出了该误差 |ε|max沿经向的分布，并可见该误差在距赤道约100 km 处的值最大，约为1 .3×10−7m/s2，并具有加速度的量纲。本文用的计量系统为 m ·kg·s制，对此制式的相对误差为 1.3×10−7(m/s2)/(1 m/s2)=0.000 013%，非常小。再者可取g′=1.67×10−4m/s2作为加速度的特征尺度，而对该特征尺度的相对误差为1.3×10−7(m·s2)/g′=0.08%，也很小。这样式（9）确实近似成立，且近似精度还较高，故而解析解式（21）至式（23）确实是式（1）至式（3）具有较高精度的近似解。

图5 | ε|max（a）、| u|max（b）和 | Φ|max（c）沿经向的分布Fig.5 The distribution of | ε|max (a)、| u|max (b)和 | Φ|max (c) along lon gitude

4.2 驻波解的空间结构和时间演变

该赤道驻波异常向赤道南北两侧的衰减快慢，这取决于值 δ=β/(2C0) 的 大小，因赤道上 β 是常数，故 δ值仅反比于越小则该驻波向赤道南北两侧衰减得越快。实际在以上三大洋中，虽和 (ρ2−ρ1）/ρ2会有些差异，但总体相近，故C0总 体也应相近，为此本文中对C0值也取得相同，故而 δ的取值也相同，这表明该驻波异常向赤道南北两侧的衰减程度也相同。图5b，图5c 分别给出了模态1 的u在t=T/4 时 在大洋中心线x=L/2处的经向分布，以及 Φ 在t=0时 在大洋西边界x=0处的经向分布。从图5b，图5c 上可见u、Φ的 最大振幅 |u|max、|Φ|max从赤道到极地的衰减程度以及该振幅被赤道所俘获，从而被限制在赤道南北各200 km 也即约2°的范围内。因δ与模态数n无关，故模态2 的情况与模态1 相同。注意到本文的 δ=β/(2C0)，与经典赤道开尔文波的表达式相同，故该驻波异常被赤道俘获的情况也与之相同。

模态1（n=1）在整个大洋只有半个波（图1，图2），其波长为赤道上整个大洋宽度的2 倍；模态2 在整个大洋有1 个波（图3，图4），其波长则为赤道上整个大洋的宽度；余类推。n越大，即模态数越高，该驻波的波长则越短。由式（17）可知，热带大洋的宽度L越宽，模态数n越低，则其频率越低，模态1 的频率最低，此时其波长也最长。与之相应，频率越低的波动其周期越长。从上述计算结果看，以上三大洋的赤道驻波异常模态1、模态2 的周期均接近或处在年际振荡周期之内。

图6a，图6b 以及图7a，图7b 分别给出了模态1、模态2 赤道上的流场以及位势场在时刻0、T/8、T/4、3T/8、T/2、5T/8、3T/4 和7T/8 的空间分布，图中以热带大洋宽度L作为1 个单位，模态1、模态2 的周期T分别取为T1、T2。这些图可清楚揭示流场与位势场异常随时间变化的驻波振荡以及驻点的分布，并丰富了第3 节中的论述。模态1 以及模态2 的流场异常在时段t∈(0,T/2)（在此T取T1或T2，下同），分别在整个大洋有东向流以及在左半大洋有东向流，右半大洋有西向流；在时段t∈(T/2,T)，则模态1 以及模态2 的流向各与前一时段流向相反；如此随时间周而复始（图1，图3 和图6a，图6b）。模态1 及模态2 的位势场异常在时段t∈(0,T/2)，分别有整个大洋西半部为正异常，东半部为负异常以及在x∈(0,L/4)和x∈(3L/4,L)区间有正异常，在x∈(L/4,3L/4)区 间有负异常；在时段t∈(T/2,T)，则模态1 以及模态2 位势场异常则各与前一时段异常符号相反，如此周而复始，并以位势场驻点为支点在其两侧呈现跷跷板变化（图2，图4 和图7a，图7b）。比较图1 至图4 和图6，图7 还可见，对各模态流场与位势场异常的配置具有 π/2的位相差，当流场异常为0 时，位势场异常绝对值最大，反之亦然，位势场异常位相要超前流场异常 π/2。

图6 模态1（a）、模态2（b）中流场异常随时间分布Fig.6 Anomalous current distribution at different time in mode 1 (a) and mode 2 (b)

图7 模态1（a）、模态2（b）位势场异常（单位：m2/s2）随时间的分布Fig.7 Anomalous potential field (unit:m2/s2) distribution at different time in mode 1 (a) and mode 2 (b)

4.3 与热带大洋流场异常模态的比较

现与实际热带太平洋流场异常的统计动力诊断结果做比较。引言中已提及，我们曾对多年热带太平洋冬、春、夏、秋季（以1 月、4 月、7 月、10 月份为代表）的流场异常做过复EOF 分析（前者）[15]，发现本文3.1 节中取模态1 计算得到的热带太平洋驻波异常（后者）的流场分布，其与前者流场异常第一模态的空间场分布十分一致；该模态流场异常在整个太平洋的赤道上及临近赤道处，均表现为同一方向的纬向流，而几乎无经向流；并大体位于赤道两侧南北纬5°之内，即该模态为赤道所俘获（参见文献[15]中图1）。后者的振荡周期如上所述为6.10 a，这正处于ENSO 3～7 a的年际变化内。在对前者第一模态做的实时间系数小波分析中，发现冬、春、夏、秋季该模态3～7 a内的年际变化均很显著。特别在春季（4 月份）前者第一模态约6 a 的年际变化是最显著的，其显著性大大超过了年代际变化，而其他3 季则反之（参见文献[15]中图4），并与后者模态1 的周期6.1 a 十分相近。这样引言中提到用波包解[11]不能解释的春季（4 月份）热带太平洋流场异常复EOF 分析第一模态的结果现在则可通过本文模态1 的驻波解来完美解释，故而该赤道驻波异常在热带太平洋中的确存在。卢姁等[15]还提出前者的第一模态是ENSO 的主要模态，本文这里则要强调的是，该文献中第一模态（异常）正是模态1 的赤道驻波异常，如此该驻波（异常）在ENSO 中的作用不能忽视，其对热带太平洋年际气候异常的贡献也应予以肯定。

再与实际热带印度洋流场异常的统计动力诊断结果做比较。我们也曾对热带印度洋10 月份的流场异常做过复EOF 分析（前者）[13]，该月份是印度洋偶极子（IOD）表现最明显的月份。本文3.2 节中取热带印度洋宽度并取模态1 计算得到的赤道驻波异常（后者）的流场分布，也与前者第一模态表层空间场的分布一致，该空间场在整个印度洋中为一致的纬向流，经向流十分小，且也为赤道所俘获（参见文献[13]中图2a）。后者的振荡周期如上所述为2.67 a，并处于IOD 的2～4 a 的年际变化周期内。在该文献中提出了前者第一模态与IOD 模态相吻合，但那里未讨论第一模态的物理本质。本文要补充的是，前者第一模态的物理本质也是模态1 的热带印度洋驻波异常，其与IOD 密切相关，并对热带印度洋气候异常的年际变化产生影响。

我们还对热带太平洋和印度洋做过一些流场复EOF 分析工作，以讨论实际热带大洋上层流场异常第一模态与气候异常之间的关系，如：长江流域梅雨丰欠[12]、两类ENSO[17]、热带印度洋WYRTKI 急流和亚洲热带夏季风[18]、印度洋冬季风及其环流等[14–16]。发现本文模态1 的赤道驻波与这些文献中有些流场复EOF分析的第一模态形态相似，本文模态1 的周期也与有些第一模态的年际变化相一致。这表明，本文赤道驻波异常解与这些文献所研究的有些气候现象关系密切，可能也是这些现象的生成机制之一。

因我们未对热带大西洋流场异常进行复EOF 分析，故这里无法对热带大西洋驻波异常做详细讨论。不过文献中通过船舶资料的主分量分析得到热带大西洋上层海温异常的第一主分量最大值出现在赤道上，其具有准两年的年际变化[19]，这与本文在3.2 节中取模态1 得到的热带大西洋赤道驻波异常周期为1.73 a，两者在年际变化上则有相似之处。

4.4 与热带大洋波包解的比较

Zhang 等[11]求出了热带大洋中的波包解（前者），现将本文的赤道驻波解（后者）与前者相比较，两者均采用同样的赤道 β平面近似下的线性化正压扰动方程组，所取的环境参数也相同，仅流场振幅取得不同。而在线性化模式中振幅不会影响解的空间形态分布和时间演变。

两者的相同之处在于：解均为纬向流，无经向流；该纬向流均为赤道所俘获，解向赤道南北两侧衰减的程度也相同。大洋东、西边界均是两者的驻点，当模态数高于1 时大洋内部也有驻点。两者的频率均正比于模态数以及经典开尔文波的相速C0，而反比于热带大洋宽度L。比较本文的图6 与前文的图1 和图4知，两者不同之处在于：两者空间形态及其随时间的演变有所差异。如本文模态1 所有时刻在整个大洋均为一致的纬向流，而前文模态1 虽大部份时刻都是这样，但也有时刻例外。这种差异导致两者频率有所不同。从物理上考虑，波动能量与频率呈正相关。前者波动振幅极值处会随时间向左右水平摆动，这会消耗能量，而后者是驻波，无此摆动。若两者能量相同，前者此摆动所需的能量就体现在后者频率的增加上，故后者频率要高于前者。在两者频率的表达式中，当模态数、C0和L取得相同时，前者的频率只有后者一半，前者的周期则为后者一倍，从而相应于前者的年际变化和年代际变化要较后者的更长。

本文与前文中都讨论了两者在热带大洋异常中的表现和作用。这里要指出，前者与后者并不相互排斥，而是相互补充，并都能解释某些特定的海洋、气候事件。如对ENSO，其冬、春季节的流场异常分布更接近本文的模态1；伴随厄尔尼诺的发生，热带中太平洋海洋上层会有海温强正异常东传，而这又类似前文模态2 中位势异常的传播形态；注意到该两者的周期又都落在ENSO 其3～7 a 的年际变化中，故而ENSO 可能与这两者都密切有关，而并非前文所述仅与前者有关。IOD 的情况也是如此。后者因周期较短，更有利于解释海洋异常的年际变化，而前者则更容易解释年代际变化。在实际热带大洋中，两者可同时存在，并各自发挥影响。ENSO 和IOD 都是复杂的海气相互作用事件，不能仅用两文的简单模型来完全概括和描写；也许两文分别能解释ENSO 和IOD 中的不同类型。

本节有关赤道驻波解的讨论表明，赤道驻波异常在实际大洋中的确存在，其还与ENSO、IOD 以及其他气候事件关系密切[20–21]，可能是其形成机制之一并产生影响；而本文能提供ENSO 和IOD 等研究的新思路，故而还是很有价值和值得肯定的；为此对赤道驻波异常做更深入的研究是十分必要和必须进行的。

5 结语

本文采用赤道 β平面近似下的线性化正压扰动方程组，引入约化重力加速度后，在满足走向南北的东西海岸刚壁边界条件下，求得了大洋赤道驻波异常的近似解析解，给出了该解的计算结果，并与实际热带太平洋和印度洋的流场异常做了比较。本文得到的主要结论如下：

（1）赤道驻波异常模态1 的流场异常在整个大洋为半波，为方向一致的纬向流，无经向流；流场异常在热带大洋中部最大，并向赤道南北两侧迅速衰减，其被限制在赤道南北两侧约2º的范围内。

（2）赤道驻波异常模态2 的流场异常在整个大洋为1 波，在大洋东、西部分纬向流的流动方向相反，也无经向流；流场异常向赤道南北两侧的衰减情形与模态1 同。

（3）决定赤道驻波异常向赤道南北两侧衰减程度的系数，其仅与约化重力加速度和上层海水标准深度之乘积的平方根，即经典赤道开尔文波的相速成反比；当该相速相同时，该驻波异常向赤道两侧的衰减也相同。

（4）赤道驻波异常的振荡频率其与模态数成正比，与热带大洋宽度成反比；模态数越低，热带大洋宽度越大，则该频率越低，相应振荡周期越长；模态1 的振荡周期最长。

（5）取各参数为典型值及模态数为1，再取热带太平洋和印度洋的宽度，计算表明，两者赤道驻波流场异常都与实际流场异常复EOF 分析得到的第一模态空间分布和年际变化相一致；这表明此复EOF 第一模态的本质是赤道驻波异常，并是太平洋ENSO 和印度洋IOD 的形成机制之一。

最后要说明的是，因本文属理论工作，对模型做了必要简化和近似，所取参数虽大体符合实际，但也不完全相同，这些都会使本文的计算结果与实际在总体一致的情况下，还存在某些差异，这也是正常及可以理解的。