基于 EDEM 的旋回破碎机新型动锥衬套研究

李亚飞，李建平

中国矿业大学机电工程学院 江苏徐州 221116

旋回破碎机已在矿山行业得到了广泛应用，是非常重要的粗碎设备。相较于颚式破碎机，旋回破碎机具有生产率高、单位能耗低、运行稳定、排料粒度均匀等优点。但是，旋回破碎机的衬板、衬套磨损严重，需要经常更换，维修费用高；再者，旋回破碎机体积庞大，增加了厂房基建费用。与国外产品相比，国内产品总体较为落后，尤其是在生产率上。以美卓矿机诺德伯格 Superior MK-Ⅱ60-89 型旋回破碎机和沈阳重型机械集团有限责任公司 (原沈阳重型机器厂，以下简称“沈重”) PXF6089 型旋回破碎机为例进行对比。沈重于 20 世纪 80年代引进的旋回破碎机技术，相当于国外的第二代技术；美卓矿机的Superior MKⅡ系于 1994年以后开始生产，是旋回破碎机的第三代技术，且在第二代技术的基础上进一步提高了生产率。相同规格下，美卓矿机的旋回破碎机生产率是沈重的 2 倍[1]。

为了提高矿山企业的经济效益，缩小与国外产品的差距，需对旋回破碎机的生产性能进行进一步研究，以提高产品生产率。旋回破碎机动锥的运动特性和衬套的几何特征是影响其生产率的主要因素。其中，动锥的运动特性主要是偏心角和主轴速度；衬套的几何特征包括锥角、曲线段高度和衬套表面特征。

1 旋回破碎机动锥衬套的研究现状

国内外学者主要针对衬套的锥角、曲线段高度与半径等参数及材料进行优化研究。龚姚腾等人[2]运用三次样条曲线的几何优化方法，以生产率、偏心角、动锥与定锥的啮角为约束，建立了破碎腔的目标函数，优化后破碎腔排料粒度的合格率与衬板的磨损情况有了明显改善，但也只是对旋回破碎机腔型曲线的优化，并没有考虑到动锥衬套的表面特征；王跃辉等人[3]对目前衬板、衬套的优化研究进展进行了综述，认为在对旋回破碎机的衬板、衬套进行优化时，既要考虑到排料粒度，又要考虑破碎腔纵向物料通过量，从而改善旋回破碎机的破碎效果，提高生产率，但在对衬套优化方面没有提到动锥衬套的表面特征；王跃辉等人[4]对衬板、衬套材料方面进行了研究，将双金属复合材料应用到旋回破碎机的衬板、衬套上，与高锰钢衬板相比，其使用寿命有所增加，动锥衬套在沿用原材质和结构的情况下，其寿命也有了很大的提升；王跃辉等人[5]运用三维扫描技术检测旋回破碎机的衬板与衬套的磨损情况，通过对衬板、衬套各个生命周期的磨损情况的捕捉与分析，得出了衬板与衬套的磨损规律，并对它们的剩余寿命进行预测；Rosario等人[6]开发了一种评估破碎机衬板剖面的创新方法，评估衬板、衬套的磨损情况，提出了 HVC 标准衬板管理策略，可节省 13% 的破碎机衬板总成本，并减少 15% 的衬板更换停机时间；Chen 等人[7]采用离散元法 (DEM) 探讨了动锥衬套的曲线高度和半径、偏心角和主轴速度对破碎腔性能的影响，通过多元非线性回归建立了破碎腔性能预测模型，并基于遗传算法(GA) 进行了多目标优化，结果表明，生产率和功率密度分别提高了 36% 和 26%。

然而，很少有学者对旋回破碎机动锥衬套的表面特征进行研究，目前大多数的动锥衬套表面都光滑或波浪形的。为了提高旋回破碎机的生产率，笔者提出了一种新型动锥衬套，即在动锥衬套表面添加球形凸起，这些球形凸起均匀分布在动锥衬套与物料主要破碎接触区表面，如图 1 所示。

图1 旋回破碎机新型动锥衬套模型Fig.1 Model of new-type mantle for moving cone of gyratory crusher

2 旋回破碎机新型动锥衬套设计

2.1 破碎腔内散体物料运动特性

在旋回破碎机的破碎腔内，由于动锥的旋摆速度不同，物料有 3 种运动状态：滑动、自由落体、自由落体与滑动并存。

当动锥的旋摆速度低于某个临界值n1时，物料以滑动方式通过破碎腔；当动锥的旋摆速度高于某个临界值n2时，物料以自由落体方式通过破碎腔；当动锥旋摆速度介于n1和n2之间时，物料以自由落体和滑动两种方式并存通过破碎腔。n1与n2计算模型如图2 所示。

图2 动锥临界转速模型Fig.2 Model of critical speed of moving cone

图2 中h1、h2分别为排料口和给料口散体物料自由下落距离。临界转速[8]

式中：α为动锥底部角；st1、st2分别为排料口、给料口动锥摆动行程。

当物料以自由落体方式通过破碎腔时，由于物料下落加速度为重力加速度，故破碎机生产率大，挤压破碎次数多，破碎产品质量高。

对于图 1 所示的新型动锥衬套来说，衬套表面带有球形凸起，增大了物料在动锥表面滑移的摩擦力，但可能不利于物料的排出。因此，动锥衬套的球形凸起在衬套表面的分布，应以不妨碍物料在破碎腔内自由下落为目标。

2.2 球形凸起结构设计

2.2.1 动锥衬套的磨损情况

旋回破碎机在破碎物料时，破碎腔内衬板与衬套的磨损并不均匀，通常上部衬板磨损均匀，且沿破碎腔纵向变化平缓，衬板与衬套中下部的磨损较为严重。文献 [2] 中，KKД-500 型旋回破碎机在破碎高铝矿时，破碎腔中下部的磨损较为严重，动锥衬套与定锥衬板的磨损区基本对称，如图 3 所示。

图3 衬板磨损曲线Fig.3 Mantle wear curve

可见动锥衬套的磨损主要集中在其中下部区域，因此球形凸起分布在动锥衬套中下部即可。

2.2.2 球形凸起的结构与分布

球形凸起主要起到保护衬套和增加破碎矿石的压力，进而提高生产率的作用。基于上述目标，对球形凸起的结构以及在动锥衬套上的分布进行分析。球形凸起在衬套上的纵向结构示意如图 4 所示。

图4 球型凸起纵向结构示意Fig.4 Sketch of longitudinal structure of spherical protrusion

因为球形凸起的结构相同，主要分析纵向相邻的2 个凸起的相对位置，即图 4 中的L。图 4 中的O1与O2是相邻 2 个凸起的球心，凸起结构的基本参数有 2个，分别是γ与r，r是球形凸起的半径。

图4 中存在以下几何关系：

进一步整理式 (1) 得：

动锥衬套的球形凸起高度H应以不妨碍物料在破碎腔内自由下落为目标，γ需以圆形凸起的总体个数与质量最小为优化目标来确定。

球形凸起在动锥衬套横截面的分布如图 5 所示。图 5 中Oi为动锥衬套第i个截面圆，i=0，1，2，3，…，N；Ri为圆Oi的半径；在圆Oi分布着j个凸起，j=1，2，3，…，mi；Oi1、Oi2、Oi3分别为相邻球形凸起的圆心；Oij为圆Oi上任意一个凸起的圆心；L为相邻横截面圆的距离；βi为 2 个相邻凸起在圆Oi上的夹角；r为凸起半径；B为破碎腔主要接触区域动锥衬套母线长度；α1为动锥的锥角。

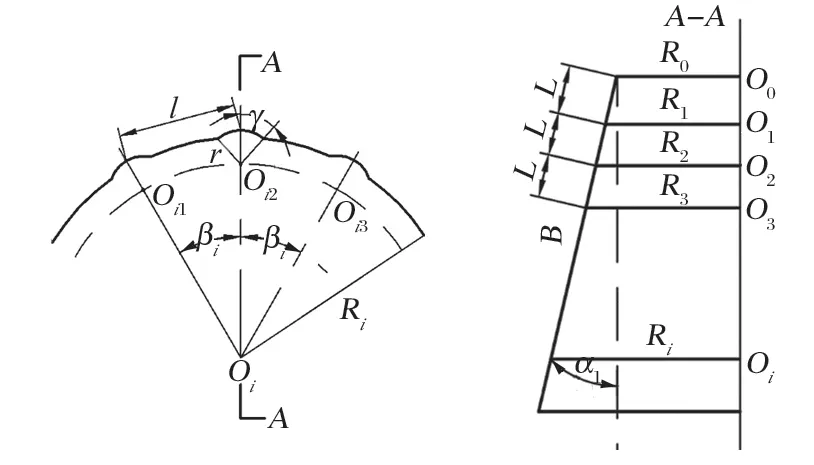
图5 球形凸起横截面结构示意Fig.5 Sketch of sectional structure of spherical protrusion

图5 中存在以下几何关系：

进一步整理式 (3) 得：

2.3 动锥衬套模型的建立

以某旋回破碎机破碎铁矿石为例进行建模。为了方便建模分析，铁矿石颗粒为正方体，边长为 300 mm，建立铁矿石的 BPM 离散元颗粒模型，该颗粒模型由正态分布单元体组成[9]。旋回破碎机的分析模型如图 6 所示，其中，α1、Hm、Hmc、d和D分别为动锥的锥角和高度、曲线段高度、上底直径和下底直径，α2、Hf、Hfc、B、b分别为定锥的锥角和高度、曲线段高度、上底直径和下底直径，具体数值如表 1所列。

图6 某旋回破碎机分析模型Fig.6 Model of a certain gyratory crusher

表1 某旋回破碎机初始参数Tab.1 Original parameters of a certain gyratory crusher

最大出料间隙

破碎机出料的最大直径为 126.15 mm，为了减少物料与动锥表面的磨损，l2应小于δ，考虑到实际铁矿石粒度并非均匀，而且动锥衬套的成本较高，为了方便计算，l2取 100 mm。

某旋回破碎机的动锥锥角α1为 11°，所以图 5 中l变化并不大，取 150 mm。在动锥衬套母线直线段分布球形凸起，考虑破碎腔主要磨损区，分布球形凸起的母线长度

为了方便计算建模，取H=25 mm，γ=30°，r=50 mm，L=150 mm。

动锥衬套凸起截面圆数量

当i=0 时，

结合式 (3)、(4)，Ri、βi、mi的数值如表 2 所列。

表2 球形凸起的结构参数与分布参数Tab.2 Structural parameters and distribution parameters of spherical protrusion

根据表 1、2 的数据，运用 Pro/E 对旋回破碎机的动锥衬套进行建模，模型中球形凸起均匀分布在动锥衬套与物料主要接触区表面，如图 7 所示。

图7 改进后的动锥衬套模型Fig.7 Model of improved mantle for moving cone

3 离散元仿真分析

离散元法是一种基于牛顿第二定律和欧拉方程，研究颗粒动力学的专业方法，近年来已被证明是研究颗粒物质流动和岩石破碎行为的有力工具。因此，离散元软件可以为模拟矿石通过旋回破碎机的流动状态和破碎效果提供计算手段。

ITASCA 公司的 PFC3D/2D 软件和 DEM-Solution公司的 EDEM 软件，是目前科研领域最具有代表性的离散元仿真软件。PFC 系列软件具有可编程性，其命令可以通过程序语言实现，开放性更强，参数设置更加精准；但是该软件对使用者的要求比较高，需要具有一定的编程能力，对于初次使用离散元仿真软件的人员来说较为复杂。相对于 PFC 软件而言，EDEM软件的使用较为简单，可以通过操作界面更加方便地对各参数进行定义，例如颗粒材料与模型、接触参数与接触模型等，所以 EDEM 软件的界面更加简洁友好。另外，由于笔者主要研究的是旋回破碎机中的生产率与破碎力，需要对破碎过程进行仿真，使用EDEM 软件可以提高仿真的工作效率。因此，选用EDEM 软件作为仿真平台，对新型动锥衬套的合理性进行验证。

3.1 仿真模型的建立

根据动锥和定锥的几何参数，使用 Pro/E 对破碎机进行三维建模，旋回破碎机改进前后模型如图 8所示。

图8 破碎机装配体半剖图Fig.8 Semi-sectional view of crusher assembly

装配体三维模型建立完成之后，需要将其导入EDEM 软件并进行相关设置，由于过程相似，仅以改进前的设置过程为例进行说明。

3.2 仿真计算过程

EDEM 软件的仿真过程包括前处理、求解和后处理 3 部分。前处理包括颗粒建模，设置颗粒生成方式，定义或导入并设置 CAD 几何模型；求解包括颗粒动力学计算，以及其他工具耦合分析等；后处理包括数据分析，3D 图片或动画的提取。

在前处理阶段完成参数设置后，进入求解仿真阶段。为了能够缩短仿真时间，使初始颗粒快速生成和落料，在颗粒生成阶段尽可能采用较大的步长，设置颗粒初始速度，如图 9(a) 所示；为了避免在颗粒替换阶段产生爆炸现象，在黏接键的形成阶段可以采用较小的步长，提高黏接键的生产质量；破碎仿真阶段是仿真的核心阶段，需要设置较长的仿真时间。本次仿真共花费 34 h，仿真过程如图 9 所示。从图 9 可知，主要的破碎区域在 C、D、E 区，证明了球形凸起分布的合理性。

3.3 仿真结果对比分析

破碎腔沿纵向分为 A、B、C、D、E、F 6 个破碎阶段 (见图 9)，取相同的物料参数分别计算每个分段改进前后的生产率与破碎力，结果如图 10、11 所示。

图9 破碎过程示意Fig.9 Sketch of crushing process

如图 10(a) 所示，1.6 s 前产量为 0，这说明物料刚刚进入破碎腔，还未发生破碎，1.6～ 6.7 s 产量近似直线上升，取稳定直线段 2.5～ 5.5 s，对应产量分别为542.94 和 1 905.63 kg，则单位时间生产率为 0.45 t/s，即1 620 t/h，对应的破碎力为 2.61×107Pa。如图 10(b) 所示，从 A 段到 B 段，破碎力保持稳定且非常小，这是由于矿石从入口进入破碎腔时，矿石颗粒和动锥没有形成稳定的相互作用；从 B 段到 C 段，破碎力显著增加，这是由矿石颗粒和动锥之间的挤压作用引起的；从 C 段到 E 段，破碎力的变化不明显，表明该区域的压缩比变化不明显；从 E 段到 F 段，破碎力急剧增加，表明离排料口越近，对矿石颗粒的破碎力越大。

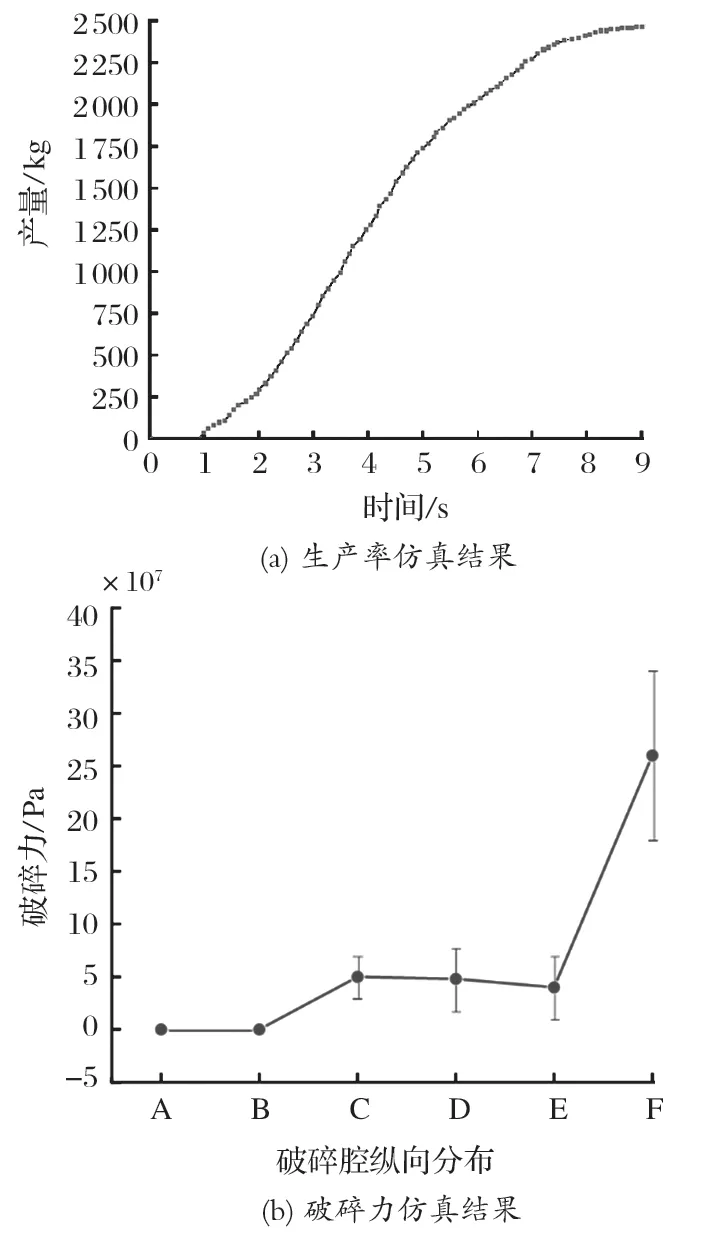
图10 改进前旋回破碎机仿真结果Fig.10 Simulation results of original gyratory crusher

如图 11 所示，D～ F 段，改进后的破碎力比改进前明显提高，表明改进后该区域的矿石颗粒得到充分破碎。取稳定的直线段 2.5～ 6.0 s，对应产量分别为403.55 和 2 296.65 kg，则单位时间生产率为 0.54 t/s，即 1 944 t/h，对应的破碎力为 5.37×107Pa。改进后生产率提高了约 20%，破碎力约为改进前的 2.1 倍，且与改进前破碎力的分布一致。

图11 改进后旋回破碎机仿真结果Fig.11 Simulation results of improved gyratory crusher

仿真计算结果表明，改进后的旋回破碎机生产率与破碎力均有明显提高，是因为动锥表面增加了球形凸起，增大了动锥对物料表面的压力，加速了物料破裂，进而增大了破碎效果，提高了生产率。

4 结语

经过理论分析，给出了旋回破碎机新型衬套表面球形凸起的结构参数 (γ、r) 以及分布参数 (βi、L)。通过离散元软件 EDEM 仿真分析，验证了新型衬套的合理性，改进后的旋回破碎机比改进前的生产率提高了 20%，破碎力提高了近 2.1 倍。

因条件有限，后续可以在现有研究基础上进一步进行试验验证，探讨转速、偏心角、定锥锥角、动锥锥角度等对破碎机性能 (如生产率、破碎力、排料粒度等) 的影响。