泵站正向进水前池“V”形导流墩整流数值模拟

刘志泉，成 立，卜 舸，袁连冲，施 伟

（1.扬州大学水利科学与工程学院，江苏扬州 225009；2.江苏省水利勘测设计研究院有限公司，江苏扬州 225127；3.南水北调东线江苏水源有限责任公司，南京 210029）

0 引 言

一些泵站在建设时，受地形及兼顾排涝要求的限制，前池设计为不规则的正向进水型式。这种不规则型式的泵站前池虽然方便施工，但容易在前池内形成漩涡和回流，导致进水条件差［1］，进而引发水泵叶片、叶轮室汽蚀［2］，不利于泵站的运行和维护。

针对泵站前池流态的改善，国内外很多学者进行了研究，其中底坎［3，4］、导流墩［5-7］、压水板［7，8］等整流措施得到了广泛应用。成立等［9］利用数值模拟方法研究底坎整流的流场结构，并分析了底坎的主要特征参数对前池流态的影响；高传昌等［10］分析底坎与压水板的联合整流机理，消除了机组振动，提高了水泵运行效率；罗灿等［11］通过在前池内设置导流墩缩小了回流区的范围，改善了进水流道进口断面的流速分布；冯建刚等［12］提出底墩和导流墩等措施来改善进水口流态，并进行了试验验证。近几年也有学者提出倒T 形底坎［13］、镂空式底坎［14］、楔形导流墩［15］等新型整流措施。本文针对某泵站不规则前池的不良流态，提出“V”形导流墩的9 种整流措施，通过数值模拟方法分析研究导流墩位置、个数、几何参数对泵站前池流态及进水池进口轴向速度分布均匀度的影响，并与试验数据进行比较，得出的结果对不规则正向进水前池的流态改善具有一定参考意义。

1 数值模拟模型及计算方法

1.1 数学模型

前池内的流动可视为三维不可压缩黏性湍流流动，RNGkε湍流模型来源于严格的统计技术，通过修正湍动黏度并考虑平均流动中的旋转及旋流情况，同时在ε方程中增加反映主流时均应变率的一项，可以很好地处理带旋流［16］。因此采用雷诺时均N-S 方程和RNGk-ε湍流模型描述该流动，其控制方程包括连续性方程、动量方程，即式（1）和式（2）。

连续性方程：

动量方程：

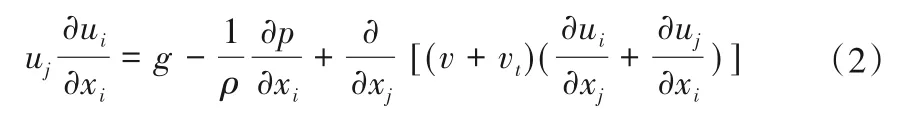
式中：ui分别为x、y、z方向的速度分量；p为压力；ρ为流体密度；g为重力加速度；ν为水的运动黏性系数；νt为紊动黏性系数。

1.2 计算域参数及网格划分

在UG NX12.0 软件构建泵站的三维流体计算域，包含引渠、涵洞、前池、进水池和各水泵的出水管。该泵站设计运行水位28.5 m，水深4.6 m；最低运行水位27.5 m，水深3.6 m，是前池不良流态产生的不利水位，本次计算对该水位工况进行数值模拟。泵站安装3 台轴流泵机组，单泵设计流量3 m3/s，叶轮直径D=800 mm。本次数值计算主要研究前池流态，以进水喇叭管和出水弯管代替泵段。计算域及其具体尺寸参数如图1所示。

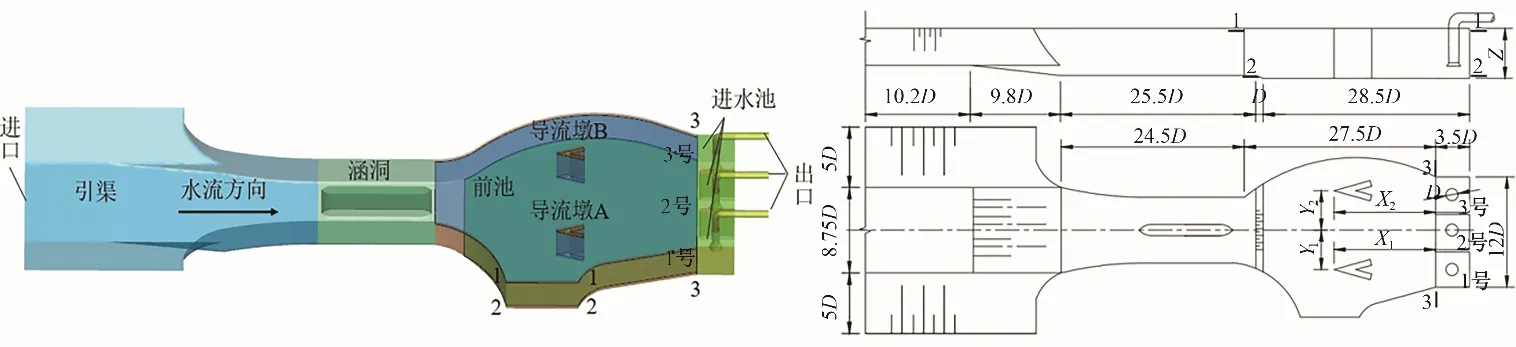
图1 计算域及其尺寸示意图Fig.1 Diagram of calculation domain and its size

在ANSYS Mesh 中对计算域采用非结构化网格划分。为保证网格质量和计算的可靠性，对前池和进水池段网格进行加密，对出水弯管壁面设置边界层，层数为6层，增长率为1.2。网格划分示意图如图2所示。

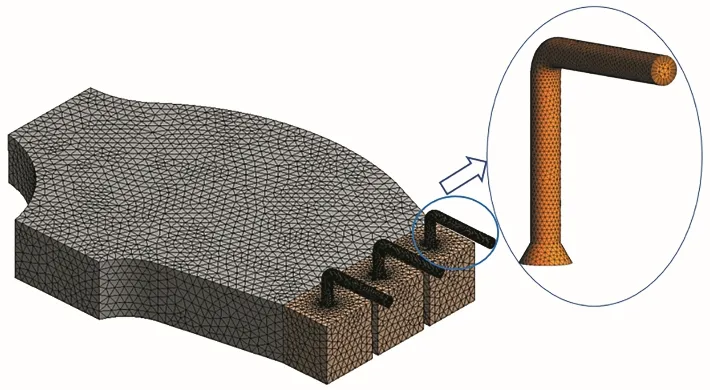
图2 局部网格划分及出水管边界层示意图Fig.2 Diagram of local mesh division and boundary layer of outlet pipe

1.3 边界条件设置

将引渠进水断面设置为计算域进口，设为质量流量进口，进口流量9 000 kg/s；进水池出水管出水侧为出口，设为自由出流条件，参考压力101.325 kPa；根据刚盖假定，自由水面设为对称边界；其余壁面为固体壁面，采用壁面函数处理；计算采用一阶迎风格式，收敛精度为10-4。

1.4 网格无关性检验

为提高计算速度，同时保证计算的准确性，对计算域网格进行无关性分析。在ANSYS Mesh中剖分8组不同数量的网格，分别为178.9 万、284.3 万、331.5 万、394.5 万、433.7 万、510.6 万、634.0 万、740.2 万个，以水力损失作为网格无关性的评价指标，水力损失的计算公式见式（3）［17］。

式中：Δh为引渠进口到吸水管出口的总水力损失；Pin为进口的总压强；Pout为出口的总压强；ρ为流体密度；g为重力加速度。

图3为不同网格数量下的水力损失，由图可知，网格数量超过433.7 万个后，水力损失基本不变，相对变化在±2%以内，本次计算选取的网格数量级为510.6万个。

图3 不同网格数量下的水力损失Fig.3 Hydraulic losses under different mesh numbers

2 研究方案

导流墩能显著改善前池中的回流和二次环流［18］，而“V”形导流墩能使水流沿其两翼扩散因而具有良好的分流作用。该前池为扩散前池，为消除前池回流区使水流更好地扩散以均匀地进入进水池，将导流墩设计为“V”形。本文研究了“V”形导流墩的9种整流方案，方案1不设整流措施，为原方案；方案2～4布置1 个导流墩A；方案5～10 布置2 个导流墩，分别为导流墩A、导流墩B，分别位于1、3 号机组前，位置由到进水池进口的距离X和距2 号机组中心线的距离Y确定（见图1）。通过对导流墩位置、长度、分叉角度3 种参数的设置，达到整流的效果。其尺寸参数如图4所示，W、L、H、θ分别为导流墩的宽度、长度、高度、分叉角度，导流墩的宽度W为0.5D，高度H高于水深，整流方案设计如表1所示。

表1 研究方案设计Tab.1 Design of the research scheme

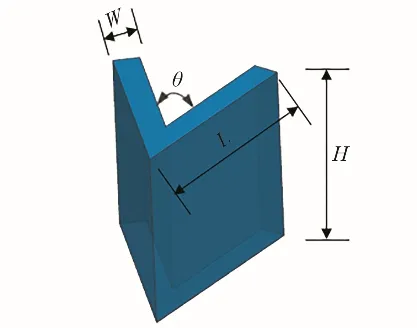
图4 “V”形导流墩及其尺寸参数Fig.4 "V"shaped diversion pier and its dimensional parameters

3 计算结果分析

3.1 特征断面和评价指标

如图1所示，选择横断面1-1（Z=4D）为面层剖面，用以研究面层的流态；横断面2-2（Z=0.5D）为底层剖面，用以研究底层的流态；选择纵断面3-3（X=0）来研究进水池进口的轴向速度分布。以轴向速度分布均匀度Vau来描述进水池进口断面轴向流速的均匀程度，计算公式［11］如下：

式中：Vau为轴向速度分布均匀度；Vai为断面各节点的轴向速度；Va为断面平均轴向速度；n为节点的数目。

3.2 无整流措施下的前池流态

原方案（方案1）下的前池面层、底层流态如图5（a）、图6（a）所示。由图可知，面层流态较为均匀平顺，底层水流通过坡降进入前池后在两侧产生大区域的回流，水流沿边壁碰撞后发生偏斜，导致1、3 号机组前进水流态紊乱。不良进水流态不仅会影响水泵性能，而且会导致前池的局部淤积［2］，因此前池底层流态是本次整流需重点研究的对象。图7 为进水池进口断面3-3轴向速度分布的试验结果与数值模拟结果，数值模拟得到的结果与模型试验结果变化趋势基本一致，证明本次数值模拟结果可信。

图7 进水池进口断面1-1轴向速度分布Fig.7 Axial velocity distribution at the inlet section 1-1 of intake pool

3.3 单个导流墩对前池流态的影响

比较图5、图6 中放置单个“V”形导流墩的方案，仅在导流墩开口附近产生小范围漩涡，这是由“V”形导流墩的形状特点引起的，基本未对面层进水流态产生不利影响。导流墩距进水池为15D时的底层流态较距离20D时的流态好，因为距离较远时，扩散后的水流又撞击到不规则边壁形成回流，未起到整流效果。导流墩分叉角度为45°时，水流的扩散比开叉角度为30°时更为均匀，但1 号机组前水流发生偏斜，并影响了2 号机组的进水流态。相较于导流墩长度为2.25D，导流墩长度为3D时扩散效果更好，前池内产生的回流区域较小。

图5 方案1～5面层流态Fig.5 Surface flow pattern of schemes 1～5

图6 方案1～5底层流态Fig.6 Bottom flow pattern of schemes 1～5

3.4 两个相同的导流墩对前池流态的影响

前池中的漩涡主要集中在底层两侧，设置单个导流墩不足以将其消除，因此设置两个“V”形导流墩方案。由图8、图9 可知，导流墩距进水口20D时的前池流态比距进水口15D时好，距离较近时水流未能充分扩散。当两个导流墩距离2号机组中心线2.5D时，导流墩未对前池两侧漩涡起到实质的破坏作用，整流效果较差；距离2号机组中心线5D时，导流墩A对1号机组前的漩涡破坏作用较小，水流经过导流墩后继续碰撞边壁，1号机组的进水流态未得到改善，导流墩B 有效地对3 号机组前的漩涡起到了消除作用，使2、3 号机组前的水流趋于平顺；距离2 号机组中心线7.5D时，导流墩靠墙壁太近未对两侧回流区起到消除作用，在两导流墩中间形成新的漩涡，整流效果差。

图8 方案6～10面层流态Fig.8 Surface flow patterns of schemes 6～10

图9 方案6～10底层流态Fig.9 Bottom flow patterns of schemes 6～10

3.5 两个不同的导流墩对前池流态的影响

由图8（c）、图9（c）可知，导流墩B 距进水池X2=20D，距2 号机组中心线Y2=5D，分叉角度为30°时，2、3 号机组进水流态较好，进水口前无漩涡，流线平顺，因此导流墩B的设计是合理的，只需对导流墩A 重新设计。导流墩A 距进水口15D时，虽然在前池中间形成了小范围回流区，但经过发展后消除，未对进水池流态造成不利影响，而且导流墩A 分叉角度无论是15°还是22.5°，均有效对1 号机组前的漩涡起到了破坏作用，分叉角度为15°时，水流更为平顺。

3.6 轴向速度分布均匀度

为定量地分析整流效果，以各机组进水池进口断面3-3 的轴向速度分布均匀度作为评价指标。原方案（方案1）与导流墩方案进水池进口断面轴向速度分布均匀度的对比如图10所示，各机组进水池进口断面轴向速度分布均匀度如表2所示。比较原方案下的轴向速度分布均匀度，1、3 号机组较低，分别为61.7%、65.6%，2号机组为79.8%。方案9、10对各机组整体轴向速度分布均匀度有明显提升，对1 号机组分别提升2.8%、17.8%，对2 号机组分别提升3.2%、2.7%，对3 号机组分别提升13.7%、9.8%。综合以上方案，方案10 对两侧机组整体的轴向速度分布均匀度提升最为明显，为最佳整流方案。如图11 所示，方案10 中1、3 号机组前的回流区消除，进水流态更加均匀。方案10 对其他工况的轴向速度分布均匀度也有所提升，只开1台机组时，2 号机组轴向速度分布均匀度为75.5%，较原方案提升4.9%；开启2台机组时，2、3号机组轴向速度分布均匀度分别为78.9%、79.9%，较原方案分别提升5.1%、8.3%。

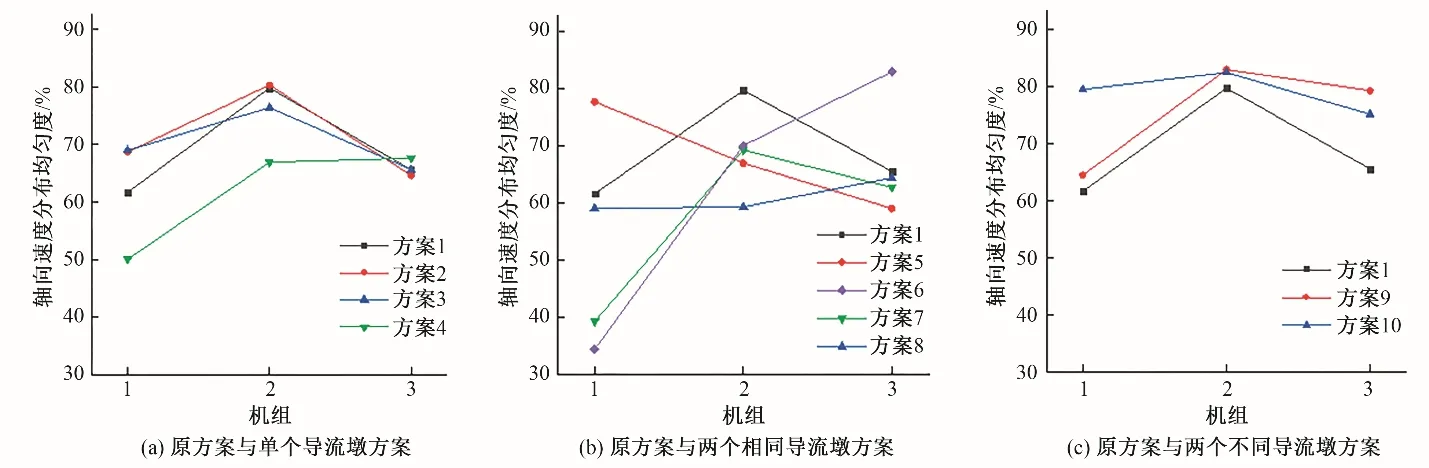
图10 各方案3-3断面轴向速度分布均匀度比较Fig.10 Comparison of uniformity of axial velocity distribution on section 3-3 of each scheme

图11 方案10前池行进流速变化示意图Fig.11 Diagram of flow velocity variation of forebay of scheme 10

表2 各方案3-3断面轴向速度分布均匀度 %Tab.2 Uniformity of axial velocity distribution on section 3-3 of each scheme

3.7 “V”形导流墩整流机理

根据对以上研究方案的分析可知，“V”形导流墩能够显著改善前池中的大区域回流。如图11 所示，当水流经过“V”形导流墩后，沿其两翼进行扩散，使流速分布趋于均匀，前池不良流态得以改善。尾后水流流速较低，在分叉口附近产生回旋，经发展后可消除，回旋范围大小与导流墩的长度、分叉角度有关，因此“V”形导流墩不宜距离进水池过近。

4 结 语

（1）原方案中，泵站前池底层两侧存在大区域回流区，通过设置“V”形导流墩的尺寸参数对前池流态进行整流，“V”形导流墩能使水流沿其两翼重新扩散因而具有良好的分流作用。

（2）单个“V”形导流墩对前池流态改善的效果有限，1 号机组前仍存在较大漩涡，且易导致2 号机组进口轴向速度分布均匀度降低。

（3）两个“V”形导流墩中的方案10 为最佳整流方案，对两侧机组进水流态有较大提升，各机组进口轴向速度分布均匀度分别提升17.8%、2.7%、9.8%。

（4）“V”形导流墩可有效消除前池中的大区域回流，在不规则的正向进水前池中得到较好的应用，研究结果为泵站前池改造提供了参考。 □