基于BP神经网络替代模型的地下水污染随机模拟

葛渊博，卢文喜，王梓博，王 涵，常振波

（1.吉林大学地下水与资源环境教育部重点实验室，长春 130012；2.吉林大学新能源与环境学院，长春 130012）

0 引 言

自2009年起，我国水利工程行业迈入了快速发展阶段，水利工程对我国社会、经济的发展及环境保护等方面大有裨益［1］。但是，水利工程的建设同样会对地下水水位及水质造成极大的影响［2］。地下水污染一旦发生，其危害巨大且深远，地下水的污染防治迫在眉睫［3］。

针对地下水污染的预测防治，一般采用地下水数值模拟方法分析污染物在地下水中的迁移转化规律以及分布情况。然而，由于自然因素和人为因素的双重影响，数值模拟模型中的水文地质参数具有高度的不确定性，从而导致模型输出结果的不确定性［4］。

近年来，不确定性分析方法在地下水溶质运移方面发展十分迅速。蒙特卡罗模拟方法是一种国内外常见的分析地下水数值模拟不确定性的方法，该方法适用于讨论多变量模型中的不确定性问题，并且可以将数值模拟模型的参数不确定性直接转化为模拟结果的不确定性，具有很广泛的适用性和简便性［5］。Hassan等［6］应用蒙特卡罗方法评价了Alaska试验场地下水模拟模型参数的不确定性；Wu等［7］提出将地下水数值模拟不确定性分析结果与风险评估相结合并且取得了很好的结果；王涵［8］将不确定性分析方法与地下水DNAPLs污染多相流的随机模拟相结合，并利用污染物浓度分布函数估算了单井遭受污染的风险；常振波等［9］分析了参数不确定性对地下水溶质运移数值模拟模型输出结果的影响，并从风险评估的角度对不确定性分析结果进行了解释。

但是，进行蒙特卡罗模拟时需要反复调用数值模拟模型，将会产生巨大的计算负荷。而替代模型既可以减少计算负荷，又可以保持较高的逼近精度。辛欣等［10］运用多元回归分析方法建立了多相流模拟模型的替代模型——双响应面模型，且替代模型精度较高；王梓博等［11］分别运用克里格方法和支持向量机法建立了模拟模型的替代模型，并选择精度较高的克里格替代模型完成了随机模拟。但是前人很少有人尝试将机器学习与随机模拟相结合应用于地下水溶质运移过程中。BP 神经网络作为应用最广泛的机器学习算法，开始在地下水领域内崭露头角。

胡伟等［12］建立BP 神经网络对平谷平原地下水水质进行快速评价，且基于BP 神经网络法的评价模型拟合度较好；潘紫东等［13］采用BP 神经网络方法建立了模拟模型的替代模型，并且使用模拟退火算法求解优化模型得到了反演识别结果。但是前人针对BP神经网络中隐含层节点数很少做具体研究。

本文根据一假想算例建立地下水污染数值模拟模型，运用灵敏度分析法筛选出对模拟模型输出结果影响较大的参数作为随机变量，为减小反复调用模拟模型产生的巨大计算负荷，再运用BP 神经网络以及克里格方法建立替代模型并比较二者精度。在运用BP 神经网络方法时，采用三分法算法快速地确定了使替代模型误差最小的隐含层节点数。然后选取精度比较高的替代模型进行输入输出从而完成蒙特卡罗随机模拟。最后，对随机模拟的结果进行统计分析与区间估计，完成地下水污染风险评价，从而对地下水污染防治提供科学依据。

1 研究方法

1.1 蒙特卡罗法

蒙特卡罗方法是一种基于随机数的计算方法，其主要思想是为了得到某个事件出现的概率或者某一个变量的期望值，可以通过做多次试验的方法，统计事件出现的频率或者变量的平均值，用该数字特征作为研究问题的解。在研究过程中无论随机事件的结果满足何种分布，在模拟次数足够多的情况下，都可以得到一个比较精确的概率分布。

1.2 灵敏度分析法

灵敏度分析法用于分析模型中某些系数或者参数的变化对最优解的影响。

在地下水模拟模型中，一个参数的灵敏度越大，则证明该参数相比其他参数更能影响模拟模型输出结果的准确性。

目前一般使用全局灵敏度分析和局部灵敏度分析两种分析方法，其中，局部灵敏度分析的计算公式如下［14］：

式中：Xk为灵敏度系数。计算Xk也可使用如下公式：

也可采取标准化无量纲形式：

本文将会采用局部灵敏度分析法评价单一参数的变化对模型输出结果造成的影响。

1.3 替代模型

进行蒙特卡罗模拟时需要大量的统计试验来完成模拟，如果直接调用数值模拟模型进行统计实验，会带来巨大的计算负荷。而替代模型可以用来代替数值模拟模型的输入输出响应关系，能够以更小的计算量得到与模拟模型相近的结果［15］。

1.3.1 基于BP算法的三层神经网络

1968年由Rumehart 和Mcclelland 为首的科学家们首次提出了BP 神经网络这一科学概念［16］，这是一种基于误差反向传播算法进行训练的多层前馈神经网络。单隐层的BP 神经网络具有较高的训练效率，可以逼近任何一个闭区间内的连续函数，完成任意大小的n维到L维的映射。

经典的BP 神经网络通常由三层组成：输入层，隐含层与输出层。计算过程分为两个阶段：前馈过程（Feed-Forward）与反向传播过程（BackPropagation）［17］。

（1）前馈过程：每个隐含层和输出层神经元输出与输入的函数关系为：

图1 BP神经网络结构Fig.1 BP neural network structure

式中：Wij表示神经元i与神经元j之间连接的权重；Oj代表神经元j的输出；sigmod 函数称为神经元的激励函数（activation function），除了sigmod函数外，常用还有tanh和ReLU函数。

将n个输入向量依次送入输入神经元，隐含层神经元获得输入层的输出并计算出输出值，最后输出层的神经元根据隐含层输出计算出回归值。

（2）反向传播过程：根据误差调整连接权重Wij的过程称之为反向传播过程。首先随机初始化连接权重Wij，对某一训练样本进行一次前馈过程得到各神经元的输出。再计算输出层的误差：

式中：Ej代表神经元j的误差；Oj表示神经元j的输出；Tj表示当前训练样本的参考输出；sigmod'(x)是上文sigmod 函数的一阶导数。

1.3.2 克里格（Kriging）方法

克里格方法将输入与输出变量之间的关系以回归方程的形式表达出来，是一种常用的地质学统计方法，并且是一种黑箱模型。

其公式如下［18］：

式中：R(xi，xj)代表xi和xj的关联函数。

高斯模型的公式如下所示：

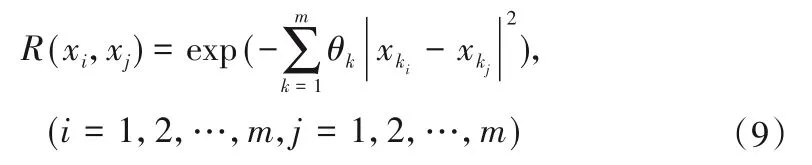
式中：θk可以通过算法求出。

1.4 三分法算法

在BP 神经网络中，隐含层节点数是一个非常重要的参数，若隐含层的节点数太少，网络将无法正确学习；若节点数太多，尽管在一定程度上可以减小系统误差，但网络学习的时间也会随之加长，而且会使训练掉入局部极小点，产生过拟合现象［19］。所以说隐含层节点数的合理设计对BP 神经网络的性能有很大影响。在本文中根据前人经验使用三分法算法［20］确定隐含层节点数，最终得到使BP 神经网络拟合效果最好的、精度最高的隐含层节点数，进而使用BP神经网络建立替代模型进行求解。

“三分法”算法流程如下所示：

式中：k为样本量；n1为隐层节点数；n为输入层节点数。当i＞n1时= 0。

式中：n为输入层节点数；m 为输出层节点数；a为1～10 之间的常数。

根据以上经验公式可得隐含层节点数的取值为［a，b］，且根据二次函数的图像性质，当最低点位于区间内时，那么该区间的斜率绝对值最小，并且左边区间斜率为负，右边区间斜率为正。

以下为三分法算法流程图见图2。

图2 三分法算法流程图Fig.2 Flowchart of the trinity algorithm

2 案例应用

2.1 问题概述

本文针对假想算例展开研究：研究区长约544 m，南北宽约555 m，面积约为0.302 km²。研究的主要对象为一层潜水含水层，将研究区概化为非均质各向同性含水层，水流为二维非稳定流。水流方向由北至南，区域内地表平坦，北侧Γ1及南侧Γ2均概化为定水头边界，东侧Γ3及西侧Γ4均概化为零流量边界。研究区内地下水补给项主要为降水入渗补给，年平均降水量约为800 mm，降水入渗系数为0.4。地下水排泄方式主要是人工开采，区内设置三口抽水井，分别是井1、2、3，且三口抽水井的抽水量均为500 m3/d，并将其作为观测井。区内有一固体废弃物堆放，经过降水淋滤，向地下水排放污染物量为5 kg/d，假设污染物不会发生化学变化以及生物转化与迁移。潜水含水层中污染物初始浓度为0。将研究区按照潜水含水层渗透系数、纵向弥散度以及给水度划分为南北两个区域（图3 中东西向实线为南北两地区的分界线）。研究区示意图及各水文地质参数表如图3所示。

图3 研究区示意图Fig.3 Schematic diagram of the study area

表1 研究区水文地质参数数值Tab.1 Values of hydrogeological parameters in the study area

2.2 模型建立

2.2.1 数值模拟

（1）地下水水流模型。

式中：K为含水层的渗透系数，m/d；H为地下水水位，m；B为隔水底板高程，m；w为源汇项；μ为含水层给水度；Γ1，Γ2为第一类边界，Γ3，Γ4为第二类边界为边界上某点（x，y）处外法线方向上的单位向量；φ(x，y，t)为已知水位函数。

（2）地下水溶质运移模型。

式中：t为时间；c为溶质的浓度，mg/L；Dx、Dy为水动力弥散系数，L2/T；ux为实际平均流速向量u在x方向上的分量；uy为实际平均流速向量u在y方向上的向量；n为含水层孔隙度；b为含水层厚度；I为源汇项；Γ1为已知浓度边界；Γ2为已知对流-弥散通量边界；Γ3，Γ4为零通量的水动力弥散通量边界；c0(x，y)，c1(x，y，t)，c2(x，y，t) 是已知浓度函数。

在已知研究区概况以及污染质运移数值模型基础之上，利用GMS 软件将研究区剖分为2886 个有限差分网格，然后利用MODFLOW 工具箱以及MT3DMS 工具箱模拟10年后研究区污染质运移情况。由于本文算例中固体废弃物的渗滤液以固定速率排出，所以仅需一个应力期并划分了10 个时间步长。10年后污染物浓度分布如图4所示。

图4 10年后污染物浓度分布图Fig.4 Pollutant concentration distribution after 10 years

2.2.2 灵敏度分析法筛选随机变量

灵敏度分析法用来筛选出对数值模拟模型输出结果影响较大的参数，并将其作为模型中的随机变量。

本文选取渗透系数K1、K2，给水度μ1、μ2，纵向弥散度α1、α2以及孔隙度n七个水文地质参数进行灵敏度分析：

首先将各参数在各自的数值参考范围内取均值输入模拟模型，得到第一组输出，再将所有水文地质参数的均值分别增加、减少10%和20%，在保证只改变其中一个参数的情况下输入到模拟模型中，得到第二组输出结果，运用公式计算三口观测井各参数的灵敏度系数值，见表2。

表2 灵敏度近似计算解Tab.2 Sensitivity approximate calculation solution

由图5可知，两个分区的渗透系数K1、K2以及两个分区的纵向弥散度α1、α2的灵敏度系数相比其他3 个水文地质参数的灵敏度系数较大。接下来将渗透系数K1、K2，纵向弥散度α1、α2作为随机变量，其他它参数作为确定性变量。

图5 灵敏度分析结果图Fig.5 Results of sensitivity analysis

2.2.3 拉丁超立方抽样

本文选择拉丁超立方抽样方法对三口观测井内的4个随机变量分别抽样取值并随机组合。根据前人经验总结，各水文地质参数的取值及服从分布如表3所示。

表3 参数概率分布及取值情况Tab.3 Probability distribution and value of parameters

运用MATLAB软件对上述参数分别抽样60组，并将其随机组合，再运用数值模拟模型求解，得到井1、2、3 的60 组污染质浓度输出结果。

2.2.4 建立替代模型

将上述四个水文地质参数输入地下水模拟模型中，计算得到相应的60 组输出。再将前50 组输入输出作为训练样本，后10 组输入输出作为检验样本分别利用BP 神经网络方法及克里格方法建立替代模型并检验替代模型的精度。

本文将基于以下3个评价指标比较两个替代模型的精度：

（1）均方误差（MSE）。均方误差表示预测值与真实值之差平方的期望值，MSE可以用来评价数据的变化程度，计算公式如下所示：

MSE的值越小，说明替代模型拥有更好的精确度。

（2）确定性系数R2（R-Square）。计算公式如下所示：

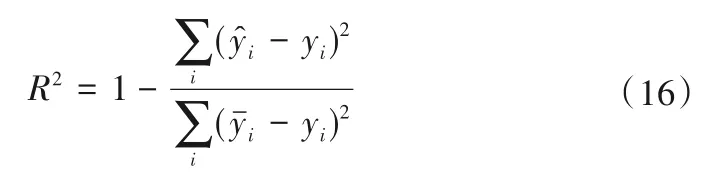
R2的取值可以用来判断替代模型的好坏，其取值范围为［0，1］，取值越接近1，则拟合效果越优。

（3）平均相对误差（MAPE）。MAPE是一个百分比值，表示预测结果较真实结果的平均偏离，计算公式如下所示：

MAPE的值越小，说明替代模型拥有更好的精确度。

上式中，m为样本个数，yi为模拟模型的输出值为替代模型的输出值为模拟模型输出值的平均值。

首先基于BP 神经网络建立数值模拟模型的替代模型，将研究区模型中渗透系数K1、K2，纵向弥散度α1、α2作为输入向量输入，将3口监测井得到的污染物浓度作为输出向量，建立了一个三层BP神经网络。

三分法算法程序运行过程中a，b，c，d（m，n均设置为0）的变化是：

（1）a=3，c=6，d=9，b=12；

（2）a=6，b=9。

根据三分法算法最终确定隐含层节点数为6，并利用matlab 软件建立了如图6 所示的BP 神经网络替代模型，其中Hidden Layer 以及Output Layer 中的W与b分别代表BP 神经网络中的参数权重与神经元偏置。

图6 BP神经网络结构图Fig.6 BP neural network structure diagram

再利用克里格方法建立替代模型，根据检验组的输入输出，最终得到两种替代模型各自的评估指标，如表4所示。

表4 替代模型精度分析Tab.4 Precision analysis of substitution model

可以明显看出，基于BP 神经网络建立的替代模型的精度高于基于克里格方法建立的替代模型。所以本文使用BP 神经网络替代模型进行随机模拟。

2.3 蒙特卡罗随机模拟

本文利用蒙特卡罗方法对地下水污染进行随机模拟。首先采用拉丁超立方抽样方法抽取上述1 000 组灵敏度较高的水文地质参数，然后将其输入到BP 神经网络替代模型中，得到相应的1、2、3号井的1 000组浓度输出，最后对这三口井进行统计分析。

3 结果与讨论

3.1 统计分析

本文利用SPSS 软件中的K-S 检验方法分别对三口观测井的污染物浓度进行分布检验，包括正态分布、指数分布、均匀分布以及泊松分布4种，其中正态分布检验结果如表5所示。

由表5 可以看出三口井污染物浓度的检验统计分别为0.019、0.023、0.018，对应的显著性水平均大于0.05，即K-S 检验接受零假设，服从指定分布，即三口井的污染物浓度均符合正态分布。

表5 单样本柯尔莫戈洛夫-斯米诺夫检验结果表 mg/LTab.5 Results of Kolmogorov-Sminov test for a single sample

分别绘制三口井的污染物浓度频数分布直方图见图7。

由图7 可知，一号井污染物浓度在370～410 mg/L 时的概率最大，为72%，二号井污染物浓度在205～225 mg/L 时的概率最大，为68%，三号井污染物浓度在120～130 mg/L 时的概率最大，为65%。

图7 三口观测井浓度频数分布直方图Fig.7 Histogram of concentration frequency distribution of three observation Wells

利用SPSS 软件得到如表6 所示三口观测井的各项统计指标。

表6 三口观测井污染物浓度统计Tab.6 Pollutant concentration statistics of the three observation Wells

由表6可以看出，三口观测井的变异系数均小于15%，可认为三口观测井污染物浓度输出的结果离散性较小，不确定性也很小。

3.2 区间估计

区间估计是参数估计的一种形式，指通过从总体中抽取样本，根据一定的正确度要求，构造出适当的区间以作为总体分布参数的真值所在区间的估计。本文将其引申，以三口观测井的浓度输出值作为要观测的参数，计算其在不同置信水平下的区间范围。

已知三口观测井的污染物浓度输出近似服从正态分布，故利用z分布进行区间估计。由表7 可以看出，置信水平越高，区间范围越大；置信水平越低，区间范围越小，且越集中在平均值附近。

表7 三口观测井污染物浓度区间估计Tab.7 Estimation of pollutant concentration interval for three observation Wells

3.3 风险评估

根据替代模型的输出结果，本文绘制出分布函数曲线图对三口井的污染物浓度输出结果进行分析。

根据三口井的不同用途，假设当三口观测井的浓度输出结果同时满足一号井污染物浓度大于400 mg/L，二号井污染物浓度大于220 mg/L，三号井污染物浓度大于127 mg/L 时，证明研究区地下水已受到严重污染。根据累积分布函数曲线图可以看出，一号井污染物浓度大于400 mg/L 的风险是0.66，二号井污染物浓度大于220 mg/L 的风险是0.60，三号井污染物浓度大于127 mg/L的风险是0.58。

图8 三口观测井污染物浓度分布函数图Fig.8 Distribution function of pollutant concentration in three

4 结 论

（1）本文运用灵敏度分析法在模拟模型的众多参数中筛选出了对模拟模型输出结果影响较大的两个参数，极大程度上降低了替代模型的维数并减少了计算负荷。

（2）本文运用三分法算法很快地确定出了使BP 神经网络精度最高的隐含层节点数。

（3）本文分别采用克里格方法以及BP 神经网络方法建立了替代模型，且确定了最优隐含层节点数的BP 神经网络替代模型具有更高的逼近精度。

（4）本文利用蒙特卡罗方法对地下水数值模拟模型中的参数进行不确定性分析，并根据随机模拟的结果完成了地下水污染风险评价，为地下水污染的防治提供了更加合理的依据。 □