变权视角下基于信息可替代性指标筛选的城市水安全评价

黄垣森，唐德善

（河海大学水利水电学院，南京 210098）

0 引 言

水是生命之源，自20 世纪70年代以来，水安全问题逐步成为专家学者研究的热点问题［3］。城市水安全是人类社会满足自身发展的前提与必要条件，而往往随着经济社会发展、城市规模扩大、人口数量激增，水安全则会成为城市发展的制约因素［1，2］。对城市水安全状况进行评价，能给有关部门提供科学决策的依据。前人已对城市水安全评价做了诸多研究，张修宇等［4］以“三条红线”为约束条件对郑州市水安全状况进行评价；薛昱等［5］基于DPSIR 模型评估广东省水安全等级；王磊等［6］基于犹豫模糊语言对深圳、佛山、广州城市水安全进行评价；孙雅茹等［7］基于博弈论组合赋权对南京市水安全进行评价，结果表明其处于基本安全的水平。然而前人的研究未对水安全评价的指标筛选予以重视，且在权重排序时，忽略了各指标之间随状态变化，其相对重要性也会随之改变的情况。笔者基于指标之间的信息可替代性，计算指标集相对于整个指标体系的信息重叠程度，剔除重复度高的指标，即可被替代的，并引入动态权重，对状态值接近阈值的指标予以加权，使用正态云模型确定指标隶属度，得到最终水安全等级。本文主要评价了2015年至2019年西安市的水安全等级情况，以期为西安市的水资源规划提供决策依据。

1 研究方法

1.1 信息可替代性指标筛选

综合评价目前被广泛应用于社会经济诸多领域，是各部门进行科学决策的基础工作。复杂的评价对象往往涉及到较多的因素，这就导致评价指标体系太过臃肿。指标体系中存在大量冗余的信息量，各指标之间互相影响，较高的信息重叠会在评价时反复强调，影响评价效率及结果，故在建立一套科学的指标体系时，指标筛选是必不可少的工作。本文出于完整性、可操作性、针对性等指标选取原则，考虑专家意见及研究区实际情况、前人研究文献，初步选取一套指标集，后利用信息可替代性指标筛选方法进行指标体系的完善。

1.1.1 信息可替代性指标筛选原理

对于初步筛选的指标集，本文引入基于信息可替代性的指标筛选方法，已有学者对此方法进行深入研究，并验证其在指标筛选方面的合理性［8］。即以指标相对于整体的信息重叠程度表示信息可替代性，首先以Pearson相关系数来定义指标与指标之间的信息重叠程度，后以除了Xi外其余指标的Pearson相关系数平方和的均值来定义指标Xi对于整体指标集的信息重叠程度，即信息可替代性。

若指标Xi的信息重叠程度远高于其他指标的平均水平，则可以认定该指标信息可替代性极大，对于整体的信息增量贡献率低，应被剔除。若某指标信息重叠度低于其余指标的平均水平，则该指标可对评价对象进行有效的描述，应保留。故本文以整体指标体系中各指标信息可替代性均值为衡量标准，大于该值予以剔除，小于该值予以保留。

1.1.2 信息可替代性指标筛选步骤

计算初选指标体系中n个指标的Pearson 相关系数矩阵R=(rij)n×n，Pearson相关系数公式为：

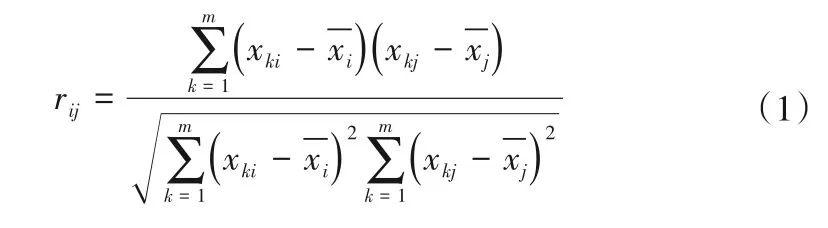
式中：rij表示第i个指标与第j个指标之间的信息可替代性，其中m表示样本数量；xki表示第i个指标对应第k个样本值表示第i个指标m个样本的均值。

剔除了Xi后，剩余的n-1 个指标Pearson 相关系数矩阵构成了一个子类Di，n-1，计算该子类中元素除对角线外其余元素的平方和的平均数，表示为指标Xi的信息可替代性Ri，计算公式如下：

以n个指标的信息可替代性均值作为划分指标是否可剔除的依据，即：

若指标可替代性不大于平均可替代性，则说明该指标所蕴含的信息较为重要，在很大程度上无法被其他指标所取代，即当满足：

则该指标应予以保留，反之剔除。

1.2 变权法

目前国内在水安全评价的研究中，所构建的评价模型里利用层次分析法、熵权法等确定的权重不随指标状态值的改变而改变。然而在实际研究中发现［9］，城市水安全等级存在明显的“木桶效应”，即当某一个指标出现极差的情况时，若该指标常权较小，则有可能会被较优且权重更大的指标“稀释”其影响，对评价结果的影响显著增大，导致常权法所评估的结果与实际情况会有较大偏差。故本文引入变权法，对常权所确定的权重进行修正，使权重随各样本状态值变化而变化。

具体计算步骤如下［10］：

先确定城市水安全评价模型的常权，本文由CRITIC 法确定，由于篇幅限制，本文不再详细介绍常权计算方法，其具体计算步骤参考文献［11］，后在此常权基础上对权重进行修正。

城市水安全评价模型共有n个指标，定义ui为指标Xi的影响度函数，表明Xi的状态，取ui∈[0，um]，um通常可取1、10、100，本文中取um=1，即当ui=0时，Xi状态为最劣，ui=um时，Xi状态为最优。

令修正后的变权权重为wi，则wi∈(0，1)，且wi= 1。

特别的，令wmi表示总体指标最优的权重，也称基础权重，该基础权重取由CRITIC 法确定的常权。又令w0i表示指标Xi状态最差，其余指标状态最好时，指标Xi对应的权重。w0i的计算公式如下：

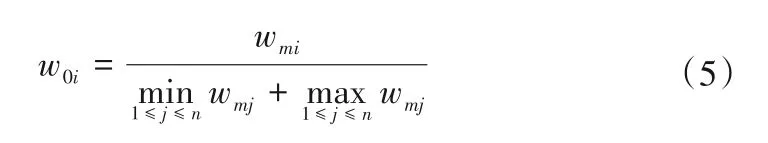
为了简易直接的获取变权权重wi，在此引入中间函数λi(u)(i= 1，2，…，n)，其在[0，um]上非负不增可微，且最大值λmi=λi(um)，最小值λ0i=λi(0)，其中λi(u)计算公式如下：

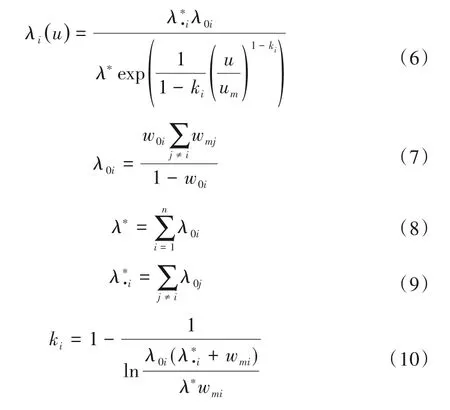
最终，经过修正后的变权权重wi为：

式中：i= 1，2，…，n。

1.3 评价方法及等级划分

云模型理论常被用于决策评价等领域，该模型综合了概率论与模糊集理论，通过算法可实现定量与定性的双向转化。其详细计算步骤不在本文中过多赘述，具体可参考文献［12］。

各指标与城市水安全评价等级共划分为五级，城市水安全评价等级见表1，各指标评价等级待实例研究时，指标筛选后列于该章节中。

表1 城市水安全评价等级Tab.1 Urban water security evaluation grade

根据云模型计算方法得到综合隶属度矩阵R后，根据以下公式结合变权法修正后的权重确定城市水安全评价等级：

式中：L为城市水安全评价等级隶属度；d为评价等级，I、II、III、IV、V分别对于d=5、4、3、2、1；wi为修正后的变权权重。

2 实例研究

本文选取西安市2015年至2019年城市水安全等级作为研究对象。西安市位于陕西省中南部，作为“一带一路”的起点城市，西安市承担着极大的发展压力。随着工业化和城市化进程的推进，水资源的过度开发、水环境污染以及水资源浪费等问题日益严峻，生态环境进一步恶化会影响到西安市国家中心城市建设进程。

2.1 指标筛选

构建城市水安全评价指标体系，应从多个方面寻找影响城市水安全级别的因素，本文统计文献及国家标准中出现频率较高的指标，并通过专家咨询，初步选取24个指标，其样本数据均来自于西安市统计年鉴、水资源公报等。

表2 西安市城市水安全评价指标初选Tab.2 Primary selection of evaluation indexes of urban water security in Xi'an

将以上24 个指标的样本数据代入式（1），得到其Pearson 相关系数矩阵，因矩阵数据过多，不在此列出。计算可替代性Ri，将得到的Pearson 相关系数矩阵中的数据代入式（2），并以此将结果代入式（3）、式（4），将计算结果列于表3。

表3 指标筛选结果Tab.3 Indicator selection results

最终计算得出10 个指标的西安市城市水安全评价指标体系，见表4。

表4 西安市城市水安全评价指标体系Tab.4 Evaluation index system of urban water security in Xi'an

2.2 指标筛选合理性检验

本文采用常权及云模型理论对指标筛选前后城市水安全评价体系分别进行评价对比，校核指标筛选合理性。

常权权重采取CRITIC法确定，具体步骤参考文献［8］，确定指标筛选前后的权重列于表5。

表5 指标权重Tab.5 Index weights

运用云模型理论进行隶属度计算时，超熵取0.01，生成2 000 个云滴，生成24 个指标的云模型数字特征表6，筛选后10个指标的数字特征也包含其中，其中Ex为期望，En为熵、He为超熵，依次代表云滴分布的中间值、云滴可被C接受的取值范围、云滴的离散程度。

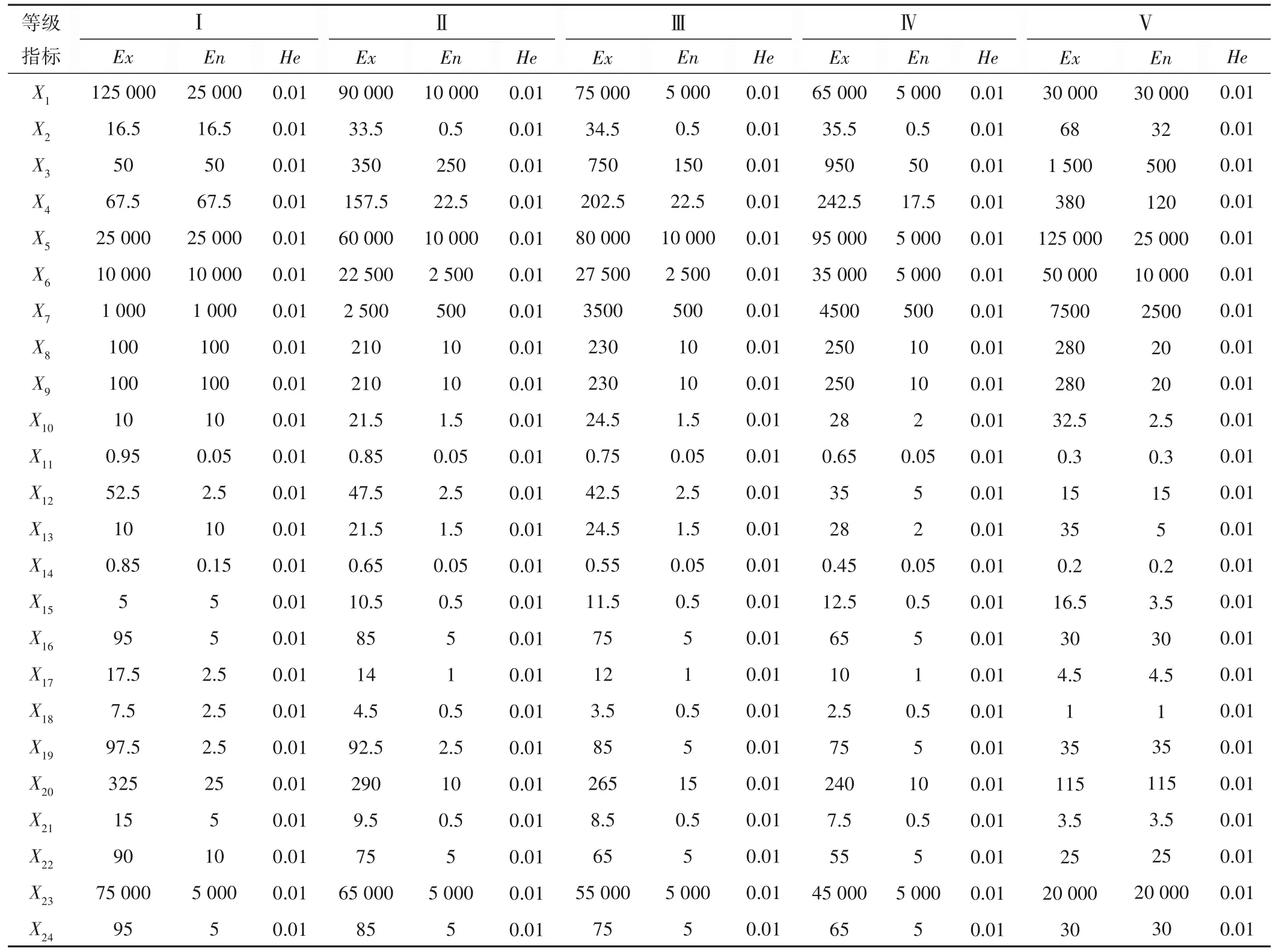
表6 云模型数字特征表Tab.6 Digital feature table of cloud model

分别得到24 个指标及10 个指标的隶属度矩阵后，依据公式（12）、（13）算出西安市城市水安全评价等级，见表7。

表7 筛选前后西安市城市水安全级别Tab.7 Urban water security levels of Xi'an before and after selection

由结果可知，由信息可替代性指标筛选法将原本24个指标删减为10 个指标后，评价结果基本与筛选前一致，可见原指标体系中，信息重叠度过高，经过该方法的筛选，不仅降低了原指标体系的信息冗余，还在保证评价结果科学合理的前提下，简化了水安全评价的指标体系。

2.3 权重修正

依据研究方法中的变权法对筛选后的10个指标修正权重，其常权已列于表4 中的第三行与第六行，根据公式（5）～（11）进行计算，得到2015-2019年修正后的权重见表8。

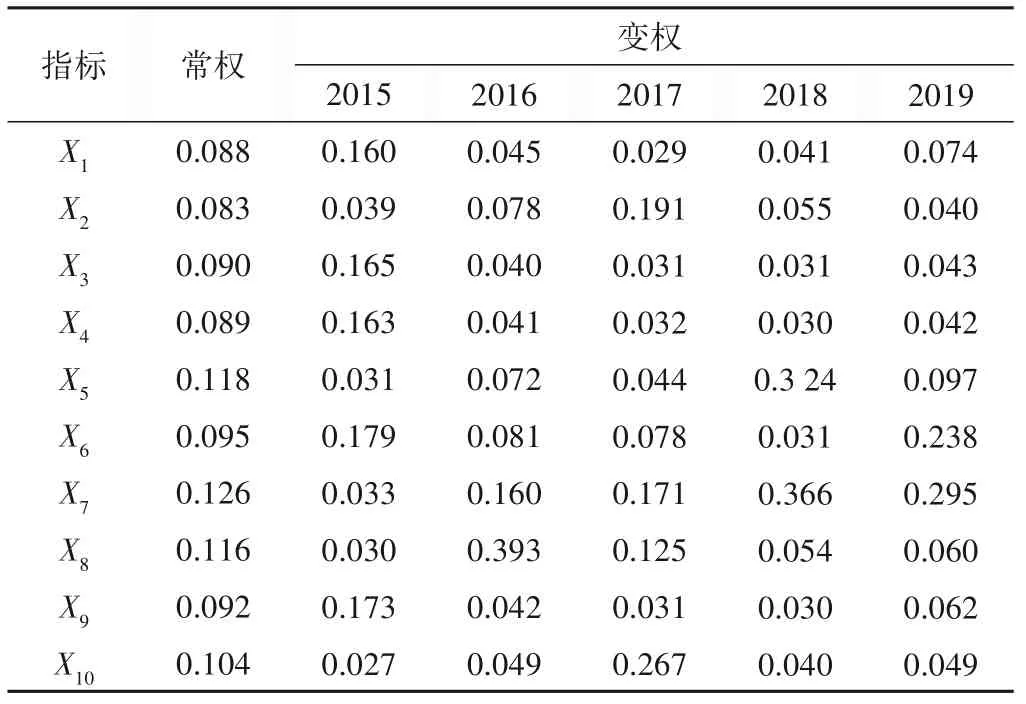
表8 修正后权重Tab.8 revised weight

2.4 城市水安全评价

参考《西安市水资源承载能力评价》等［12-21］前人研究文献，在此基础上咨询专家意见，结合地区实际情况，确定最终10 个指标的分级标准。

根据云模型理论，取超熵为0.01，2 000个云滴，生成综合隶属度矩阵，依照公式（12）、（13），带入2015-2019年修正后的变权权重，得到西安市水安全评价等级见表10，其趋势变化如图1所示。

表10 变权前后西安市水安全评价级别Tab.10 Urban water security levels of Xi'an before and after weight revised

2.5 结果分析

由图1 可知，西安市水安全评价等级总体而言呈现上升趋势，无论是常权或是变权结果大体一致，仅2015年处于Ⅲ级，其余年份均处于Ⅱ级，但其增长趋势已逐步放缓。西安市作为全国严重缺水城市之一，水安全一直是制约西安市发展的“短板”。

受限于西安的自然区域因素，当地水资源总量严重不足，自2018年起，西安市几次升级户籍政策引进人才，导致人口密度飙升，给城市水安全带来了极大的压力。2019年，全国人均水资源量2 077.7 m3，然而西安市人均水资源量仅为239 m3，不足全国平均水平的1/8。近几年西安市节水型社会建设卓有成效，人均日用水量有显著降低。但西安市水资源形式仍十分严峻，全市应实施更严格的水资源管控，积极推进引湑济黑、引汉济渭等引调水工程建设，从根本上增加西安市水资源总量。

在水资源供需不平衡的压力下，西安市主要依赖地下水源供水，对地下水资源开采力度极大，导致地表、地下水资源明显下降。2015年至2018年，西安市人工地下水回灌量逐年增加，但2019年由80.02 万m3骤降至68 万m3，给西安市水安全带来了一定的隐患。地下水资源过度开采易造成地面沉降、区域水资源衰减及水污染扩大，西安市在此方面应加强地下水资源开采管理，加大人工地下水回灌量，涵养地下水源，改善西安市水文状况。

近几年西安市经济飞速发展，工业在带来客观经济效益的同时，也给城市水安全带来了极大的压力。2015-2019年间，第二产业占生产总值比例呈现先下降再上升的趋势，西安市应调整产业结构，降低水耗较大的工业比例，提高水耗较低的服务业比例，同时提高工业节水技术，以减轻城市水安全压力。

有效灌溉面积能在一定程度上反映地区水利化程度，西安市有效灌溉面积逐年升高，但由于部分区域水利灌溉工程年久失修、长期无水、退耕等原因，2019年由18.86 万hm2降至16.38万hm2。西安市应加大灌区建设，推广节水灌溉设备，提高农业水利化程度，以保证西安市有效灌溉面积保质保量增长。

采用变权法对常权进行修正后，评价结果相对于常权法显示出较大的区分度，由图1 可知常权法确定的西安市水安全级别五年均为上升，而变权法确定的西安市水安全级别2019年较2018年有所下降，原因为变权函数敏感的发现了2019年有效灌溉面积及地下水回灌量等指标的状态的异常变动，对其进行惩罚，放大权重，使评价结果更为合理。

图1 城市水安全变化趋势Fig.1 Trend of urban water security

3 结 论

（1）2015年至2019年，西安市城市水安全级别呈现先上升后下降的趋势，其主要限制因素为人均水资源量、地下水回灌量、工业占生产总值比重、有效灌溉面积，西安市有关部门应采取针对性措施，合理配置水资源，实现城市水安全的稳步提升。

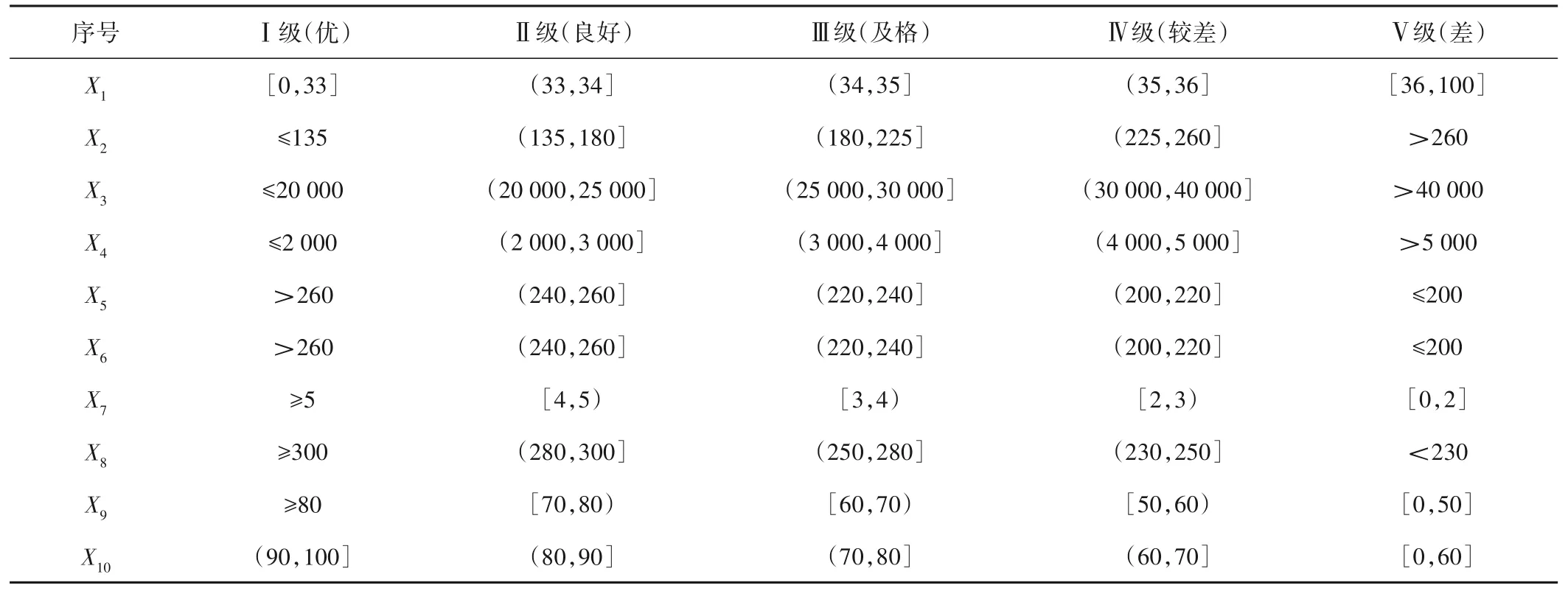
表9 评价分级标准Tab.9 Evaluation grading standards

（2）将信息可替代性指标筛选方法用于城市水安全评价指标体系构建中，消除了指标体系的信息冗余度，并与筛选前指标体系进行对比验证，结果表明该方法在很大程度上保留原指标体系所能表示的信息量，有利于提高评价效率。

（3）前人大多采用常权对城市水安全进行评价，本文引入变权思想，有利于防止短板指标被优势指标“中和”其影响，结果显示，变权法相较于常权显示出较大区分度。 □