双船拖曳系统运动响应研究

刘永强，许 冲，王志博

（1.海鹰企业集团有限责任公司，江苏 无锡 214000；2.江苏海洋大学海洋工程学院，江苏 连云港 222005）

0 引言

双船拖曳探测是常用的拖曳探测方法，采用的双船拖曳系统由2 艘母船、缆绳和众多拖曳缆-体结构组成。双船拖曳系统的拖曳体沉深较小，由于两船在航行时需相互配合，不适用高速拖曳，两船需协同对拖曳绞车进行水面操纵。虽然双船拖曳系统将探测区域限制在随船前进的小范围内，搭载声学探测设备的拖曳体易受母船螺旋桨的影响，但其可结合滑索结构释放多个探测设备，实现高效率的宽面探测活动。该系统在浅海区域地质调查、河道采样等工程环境中应用广泛。WU等和朱艳杰等等均将拖曳缆看作柔性、表面光滑、不考虑塑性变形作用的拖曳缆，采用凝集参数法模拟缆的受力和运动；王飞基于凝集参数方法建立了模拟拖曳系统的方法，将缆近似看作不考虑弯矩和扭转的柔性光滑圆形截面的缆，忽略缆的弯曲刚度和阻尼，以及扭转刚度和阻尼，对于放缆长度较大的缆，弯曲和扭转的效应较为微弱，形成的结构作用力和阻尼力效应不显著。王志博等基于有限元方法概念，从刚度、质量和阻尼的角度建立了较为全面的模拟拖曳缆的有限元模型。孙洪波等为建立更为完备的船缆体耦合系统，考虑了船体操纵与拖曳系统操纵的耦合操纵性。WANG等基于ABLOW等的模型，单独考虑缆体结构对不同操纵参数的运动响应。GOBAT等建立了耦合扭转与弯曲效应的有限差分求解方法，但该方法存在一定的数值不稳定性。

基于此，GROSENBAUGH模拟了拖曳系统的回转运动的响应模型。经典的凝集参数方法对缆的张拉强化作用考虑得不够全面，VAZ等、HUANG等和VASSALOS等的模型就是缺乏结构阻尼描述的典型模型。本文基于阻尼和缆内张力对刚度强化的相关认识，将结构阻尼加入凝集参数法的体系中，在建立缆索动力学方程的基础上，结合双船拖曳系统的边界条件，采用凝集参数法建立动力学模型，并运用有限体积法求解该模型，对双船拖曳系统的动力学响应进行系统的模拟。同时，总结出双船动力学系统的运动规律和受力特性。

1 动力学模型

系缆结构的两端一般是固定在可动或静止的结构物上，比如该双船拖曳系统的两端系缆均连接在具有拖曳速度的母船上。对于浮标等结构的锚固缆，缆的一端固定在水底，另一端连接在浮标底部，随浮标一起运动。可建立唯一的坐标系，用于描述缆的受力和运动。缆上的任意一个缆段都受到重力、浮力、附加质量力、张拉力、结构黏性阻尼力和水流阻力等载荷的作用。由于缆的轴向刚度随拖曳缆的张拉状态的变化而变化，在张力沿着缆变化过程中，缆的阻尼也随之变化，本文对结构阻尼进行补充建模，模拟拖曳缆受到的结构阻尼力作用。将缆离散为足够多的节点，重力、浮力、附加质量力和水流作用力等分布力“凝集”在节点上，为了对缆的结构黏性阻尼建模，将节点与节点之间的连接简化为弹簧与阻尼器的组合单元连接，模拟缆受到的张力和结构黏性阻尼力等。

1.1 分布力的建模

图1 为缆元的全局坐标系、受力和节点编号，将缆离散为N个节点，节点编号从缆的一端开始，依次为0，…，i-1，i，i ＋1，…，N，（1 ＜i ＜N-1），在时刻j节点i与节点i ＋1 的空间位置矢量的差为

图1 缆元的全局坐标系、受力和节点编号

对于缆段受到的张拉作用力，有

若缆受拉伸作用之后伸长，则在下一时刻缆受拉伸的长度为

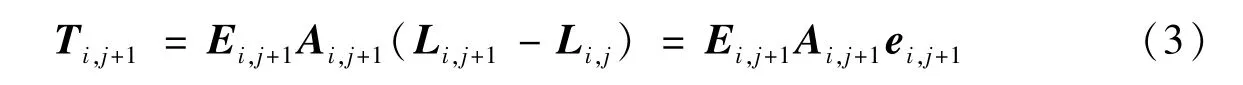
节点处的重力G和浮力B为

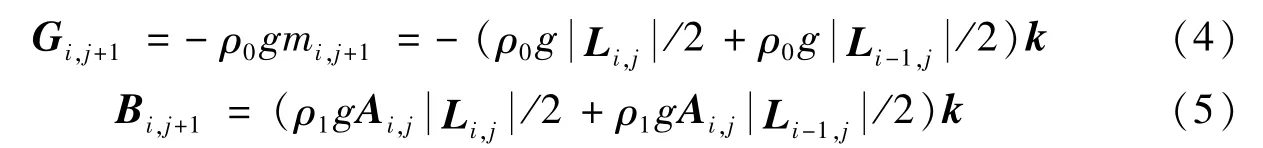
式（1）～式（5）中：i为离散节点序号；j为时间节点序号；T为缆段张力；L为缆段i的长度；R为位置；E为缆的弹性模量；A为缆的横截面积；ε为应变；ρ为缆的密度；ρ为水的密度；k为单位矢量。

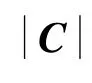
则节点处的水流阻尼力可写成

附加质量力E与水流的加速度有关，即

式（6）～式（9）中：i，j为单位矢量；Δt为时间推进步长；C、C和C分别为三个方向的阻力系数；a 为水流加速度；E为附加质量力；m为拖曳缆段的附加质量系数。

1.2 张力与结构黏性模型的应用

由于2 个节点之间的张力是恒定的，2 个以上节点之间的张力会发生变化，产生黏性阻尼的作用，因此可利用离散成为空间缆元之后节点所属的2 个缆段的张力变化量建立黏性阻尼模型。按照CRUZ 等和CHENG等对采用瑞利阻尼模型模拟结构阻尼模型的特性的分析，缆索系统受到的阻尼力可写成与张拉刚度强化作用和质量属性的定量关系，在本文中将其写成

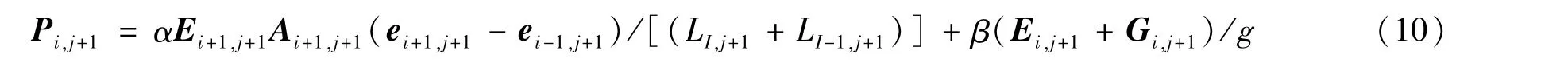
式（10）中：α和β为阻尼系数，与缆的结构参数有关，根据缆绳的试验数据，取α =0.0024，β =0.018。若缆悬挂了拖曳体，可将拖曳体看作质点，则该拖曳体同样受到水流作用力、重力、浮力和附加质量力等各种力的作用，这些力的合力为S，在此不进行详细分析。

根据牛顿第二定律，上述作用在节点处的作用力的合力等于节点的的运动加速度与质量的乘积，即

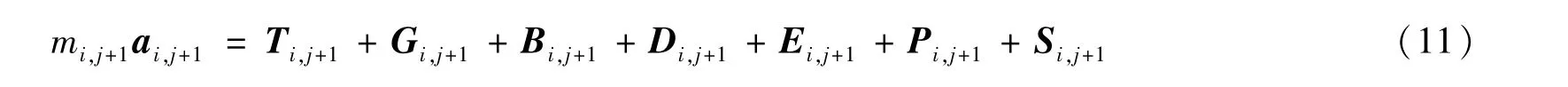
上述关系式组成了关于节点的速度的一阶常微分方程组，但含有水流阻力造成的二次项的方程组。对于双船拖曳而言，由于2 个缆段分别给定了拖曳速度（U，V，W）、（U，V，W）为第一类边界条件，缆段节点处受到的作用力为

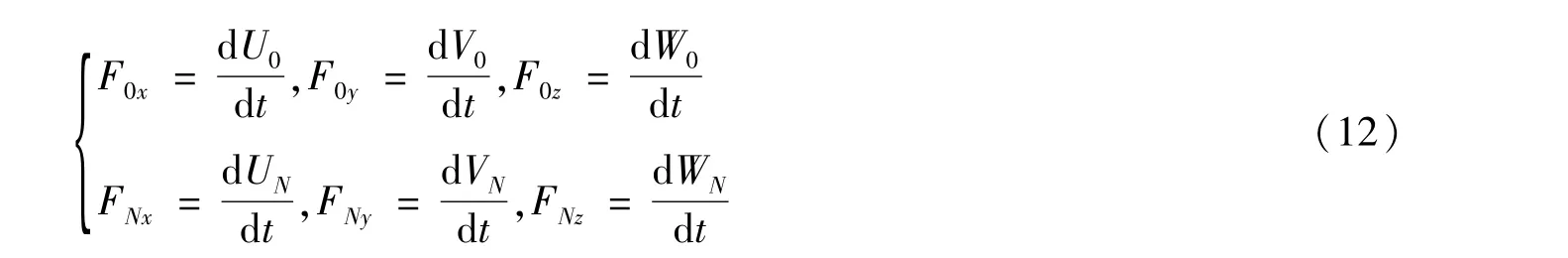
在给定初始条件的前提下，可结合2 个第一类边界条件，利用已有的数值计算库中的Newton 法求解该方程组。

在对定常缆型的计算中，可将Δt看成控制迭代步长的控制器，将时间步长取为1，通常历经多次迭代之后即可收敛到一定的缆型。对于非定常的缆型，将时间步长取得足够小能获得缆的运动响应。

利用编制的程序对HUANG等给出的全回转运动进行计算验证。

拖曳系统的结构参数：缆径为0.047 m；缆长为300 m；EI=9×10N／m；缆线密度为5.4 kg／m；阻力系数C和C为1. 2 和0. 001；拖曳体重量为3000 kg；拖曳体阻尼力系数C、C和C均为1.0；拖曳体迎流面积S、S和S均为0.5 m；拖曳体体积V为0.354 m。运动参数：回转半径为150 m；回转速率为2 m／s。

图2 为数值模型的对比验证结果，显示了水平面内运动轨迹与HUANG等计算结果的一致性，而升沉运动与HUANG等计算得到的沉深平均相差1.8%，说明在拖曳系统回转过程中，水流阻尼力引起的拖曳缆弯曲造成拖曳体的沉深略有减小。若拖曳体的重量减小，则拖曳体的沉深会因回转中的阻尼作用进一步减小。

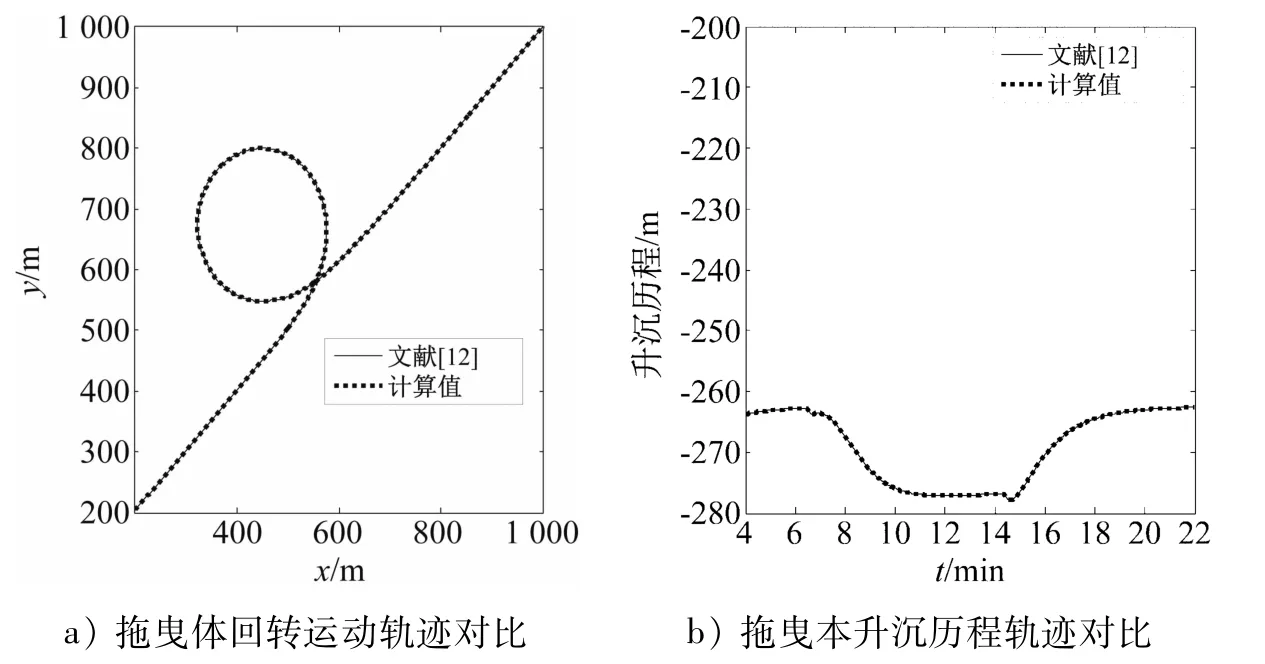
图2 数值模型的对比验证结果

2 定常双船拖曳

双船拖曳系统主要结构参数和水动力学特征如下。将拖曳体简化为质点，只考虑拖曳体受到的水流阻力、重力和浮力。

1）双船间距（见图3）：D=100 m，200 m，300 m，400 m，500 m，600 m，800 m，1000 m；D=0 m，100 m，200 m，400 m，600 m。

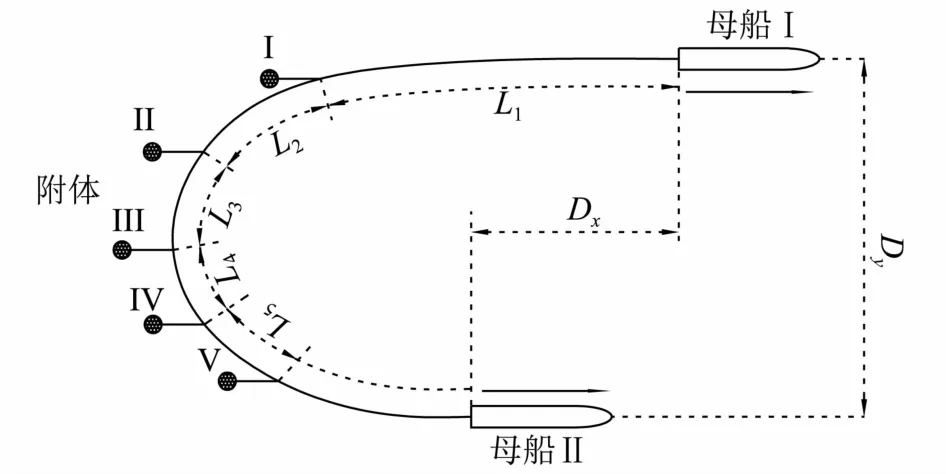
图3 双船拖曳的结构参数和位置参数

2）两母船之间的放缆长度L = 300 m，500 m，1000 m，1500 m，2000 m。

3）拖曳缆绳间距：L=30%L；L=10%L；L=10%L；L=10%L；L=10%L。

4）直航拖曳速度（双船相同）为2 m／s，3 m／s，4 m／s，5 m／s，6 m／s。

5）拖曳体的水动力学参数：三向湿表面积投影为S=0.33，S=0.35，S=0.33；三向阻力系数C=0.6，C=0.8，C=0.6；排水体积为0.107 m；水中重量（重力与浮力差）为75 kg。

图4 和图5 分别为缆长为300 m和1200 m的拖曳母船在相同放缆长度、相同船间距和不同拖曳速度下的空间缆型分布。由图4 和图5 可知，随着拖曳速度的提高，缆的沉深逐渐减小，但双船拖曳体系统远端与母船的距离并没有发生显著变化，这是由于双船拖曳形成的沉降深度小，属于浅水拖曳，水流阻尼力的抬升高度相对于远端距离是小量。为获得较为显著的缆型对比，给出放缆长度达到2000 m的双船拖曳系统在两船间距不断增大的情况下的空间缆形分布（见图6），虽然拖曳速度相同，但随着双船间距的增大，拖曳系统的沉深减小，在扫测面增加的同时，缆受到的张拉作用增强，缆的沉深显著减小。

图4 缆长300 m拖曳母船横向间距（x=0 m，y=100 m）的不同拖曳速度的缆型

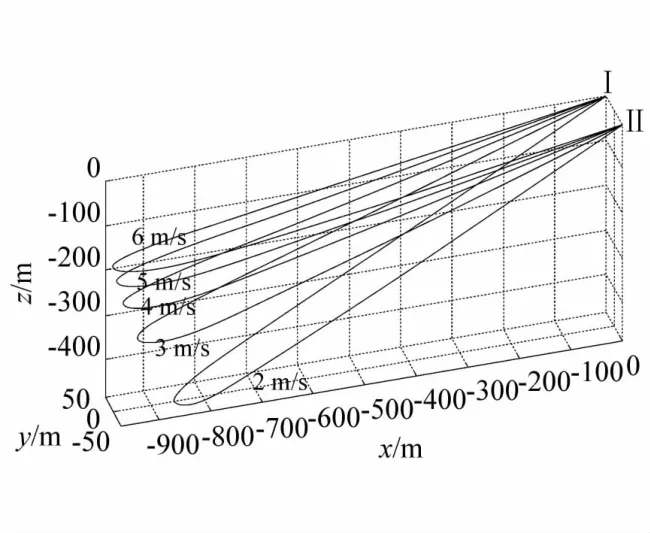
图5 缆长1200 m拖曳母船横向间距（x=0 m，y=100 m）的不同拖曳速度的缆型

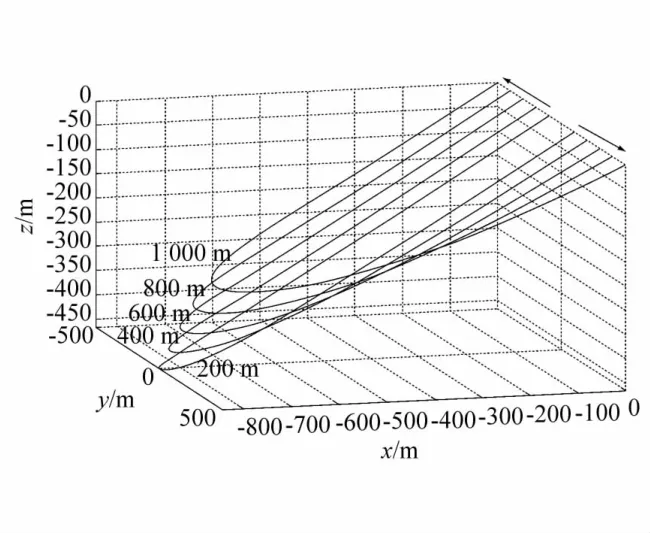
图6 缆长2000 m拖曳母船纵向间距（x=0 m，拖曳速度2 m／s）的不同纵向间距的缆型

3 波浪中双船拖曳运动响应

拖曳系统是一种低阻尼系统，相比单船拖曳系统，双船拖曳系统受到的水流作用力和阻尼行为更加显著，为模拟拖曳系统在波浪中的运动响应，设置拖曳系统的母船端因受到波浪扰动而形成的周期性扰动运动，运动规律服从正弦规律。利用本文建立的动力学模型模拟该运动响应规律，有

式（13）中：此处令A=A=3 m，ω=2π／8 Hz。图7 为5 个悬挂的拖曳体的升沉历程，由于双船拖曳系统具有低阻尼性质，对运动的传递衰减的情况为水下端的振幅与水面端的振幅之比为15.6%。与单船拖曳相比，双船拖曳虽然存在2 个传递振动的振动源，但水流阻尼与结构阻尼对振动的衰减较为显著。

图7 缆长300 m拖曳母船横向间距（x=0 m，y=200 m）拖曳速度2 m／s对应拖曳体升沉历程

4 结语

1）建立了含有结构阻尼模型的凝集参数计算方法，模拟了阻尼较为显著的双船拖曳系统的运动。双船拖曳是一类浅水拖曳系统，缆受到的水流阻尼力和结构阻尼力使得沉深变小，即使放缆长度较长也不能取得显著的沉深。

2）在相同拖曳速度下，双船间距增大，沉深减小；在相同双船间距下，拖曳速度增大，沉深减小。

3）由于阻尼作用增强，拖曳缆对水面扰动的抵抗能力增强，水面扰动的消减作用显著，在放缆长度较长的情况下可起到良好的抵抗扰动的效果。

4）双船拖曳系统的阻尼拖曳航速影响大，拖速增大，阻尼减小，扰动传递效应增强。