不同负载工况下单相半波可控整流器的Simulink仿真分析

张厚升， 靳 舵， 赵艳雷， 蒋俊杰， 王 傲

（山东理工大学电气与电子工程学院，山东 淄博 255049）

0 引 言

整流电路是电力电子变换器中最早出现的一种变换器［1-4］，其基本作用是实现电能的交流-直流变换，供给直流设备用电。整流电路的实际应用极为广泛，如在同步发电机的励磁装置、直流电动机闭环调速系统、高频开关电源、通信电源和电解电源中都有应用［5-8］。

典型的单相可控整流器通常包括单相半波可控整流器、单相全波可控整流器以及单相桥式半控整流器等。单相半波可控整流器是整流电路中结构最为简单的一种，虽然它的变压器存在直流磁化问题导致实际应用较少，但它是最基本的电路，而且对分析感性负载电路、电动机调速系统、续流回路等是非常关键的。目前的电力电子技术相关教材中基本上都介绍了带电感负载、阻感负载和带二极管续流回路的单相半波可控整流器的相关原理，但对纯电感负载基本上鲜有介绍。而且对于感性负载电路，学生普遍感到难于理解与分析，本文借助Simulink虚拟仿真软件［8-12］，主要剖析了单相半波可控整流器的纯电阻负载和纯电感负载工况，进行了理论分析与建模仿真，为电力电子技术和直流电动机调速系统注入探究性、创新性元素，有助于实现以学生为中心的自主学习。

1 单相半波可控整流器常见案例

某同步发电机励磁装置采用晶闸管构成的单相半波整流电路，如图1 所示。交流电源电压峰值为220 ×，频率为50 Hz，所带负载性质分为两种情况：纯电阻负载，R ＝2 Ω；纯电感负载，L ＝10 mH。

图1 晶闸管构成的单相半波可控整流器

2 纯电阻负载时单相半波可控整流器案例与仿真分析

实际电力电子装置的负载中，属纯电阻性质的负载有很多，例如：电阻加热炉，电吹风，电解装置等［13］。

所建立的纯电阻负载工况时，单相半波可控整流器的仿真模型如图2 所示。仿真建模参数与案例所给参数相同，仿真模型中触发器采用同步6 脉冲发生器［14-16］，将同步信号AB接至电源电压测量模块，其余端置零，控制角取α ＝30°，采用Demux 模块取6 路驱动信号中的一路作为晶闸管的触发信号，其余信号悬空不用。脉冲触发信号的频率为50 Hz，幅值为1 V。负载模块采用Series RLC Branch 模块，由于是纯电阻负载，模块仅设R ＝2 Ω，仿真时间为0 ～200 ms，采用ode45 仿真算法。

图2 纯电阻负载时单相半波可控整流器的仿真模型

仿真分析过程中，假定晶闸管VT 为理想电子器件，即器件导通时晶闸管VT 的管压降为0，关断时晶闸管VT的漏电流为0，器件的开通与关断瞬时完成状态的变换。图3 给出了单相半波可控整流器的输入电压u2、脉冲驱动信号ug、整流器输出电压ud、电流id、晶闸管两端电压uVT的仿真波形，由图中可见，由于负载为纯阻性，电流的仿真波形id和整流器输出电压ud完全相同，而且二者成正比，这也正是电阻性负载的特点所在［9］。

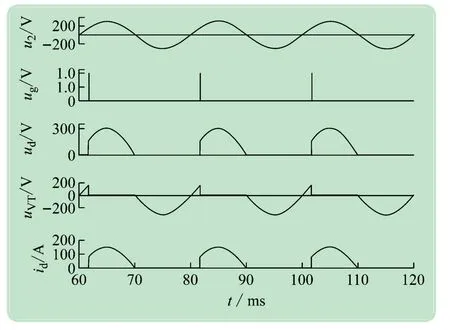
图3 单相半波可控整流器的仿真波形

在电源u2的正半周（60 ～70 ms），触发器在α ＝30°时发出脉冲信号使晶闸管VT导通，负载电压ud＝u2，电流id＝ud／R ＝u2／R，晶闸管两端承受的电压uVT由导通前的u2变为0。在70 ms时，电源电压u2＝0，则电流id＝u2／R ＝0，晶闸管VT 由开通变为关断状态，晶闸管两端承受的电压uVT由0 再次变为u2，此时晶闸管开始承受反向电压并处于关断状态，直至下一周期晶闸管的触发脉冲来临使其导通为止。对于晶闸管VT而言，当它处于导通状态时，其承受的电压为0，当它处于关断状态时，其承受的电压为电源电压u2，从其仿真波形上可以看出，晶闸管VT 承受的最大反向电压等于输入电源u2的峰值，即：uVTmax＝220 ×＝311 V，由于晶闸管VT 与负载属于串联连接，所以流过晶闸管VT的电流等于负载电流id。

图4 分别给出了α ＝0°、α ＝90°、α ＝120°时单相半波可控整流电路的工作情况，比较图中的电压波形可得：控制角α 越大，单相半波整流器的输出电压越小，晶闸管单相半波整流器控制角的移相范围为α∈（0° ～180°），整流器输出电压ud的仿真值和计算值的比较见表1，由表中可见，Simulink 仿真结果与实际计算结果在误差范围内是完全相符的，由此也说明，通过仿真分析电路的工作状态是完全可行的，而且仿真对于电路的设计与分析是十分有用的。

表1 整流器的输出电压仿真值与理论计算值的比较

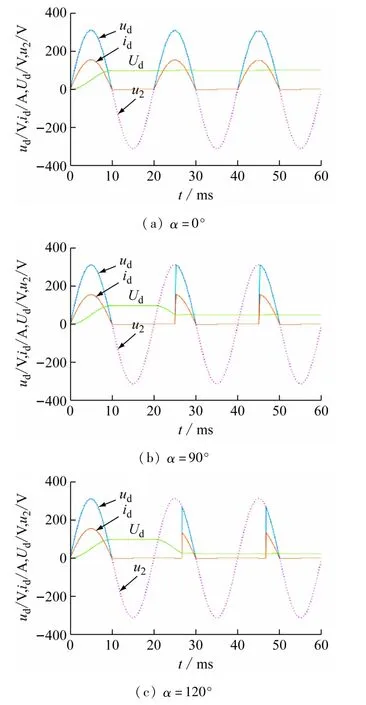
图4 不同控制角α时单相半波可控整流器的电压电流波形

3 纯电感负载时单相半波可控整流器案例仿真与分析

3.1 分段定量分析

若是阻感负载，当晶闸管VT导通时，整流器的输出电压立即跟随电源输入电压，输入电压过零变为负值后，由于电感的储能作用，晶闸管不能立即关断，输出电压会继续跟随电源输入电压变为负值，直到电感电流下降至零时，晶闸管才会关断。对于整流器的电流来说，整体上是滞后于电压的。这仅仅是对带阻感负载工况的单相半波可控整流电路的定性理解，但对于纯电感负载来说，仅依据这些很难进行工作情况的判断，为此本文借助Simulink对其进行仿真。

在此将晶闸管VT 视为理想电力电子开关器件，忽略开通过程和关断过程，则晶闸管可以认为只工作于通态或者断态。那么单相半波可控整流器可以认为是晶闸管控制的分段线性电路［11］，在每一种状态下满足不同的微分方程。假定晶闸管的控制角为α，则导通角为θ，那么在一个开关周期（0，2π］内，整流器的输出电压满足：

因此有cos α ＝cos（α ＋θ），亦即控制角α 与导通角θ满足关系式

3.2 实例分析

（1）当α ＝0、θ ＝2π 时，单相半波可控整流器输出电压

输出电流

输出电流的均值

输出电流的有效值

（2）当α ＝π／3、θ ＝4π／3 时，单相半波可控整流器的输出电压

输出电流

输出电流的均值

输出电流的有效值

3.3 仿真与分析对比

将图2 所示仿真模型中的Series RLC Branch模块设为电感负载，且设L ＝10 mH，仿真模型就变成了纯电感负载的单相半波可控整流器，其余仿真参数与前面纯电阻负载相同。分别将控制角设为：α ＝0°和α ＝60°，重新启动仿真可得单相半波可控整流器在纯电感负载时的波形，如图5 所示。

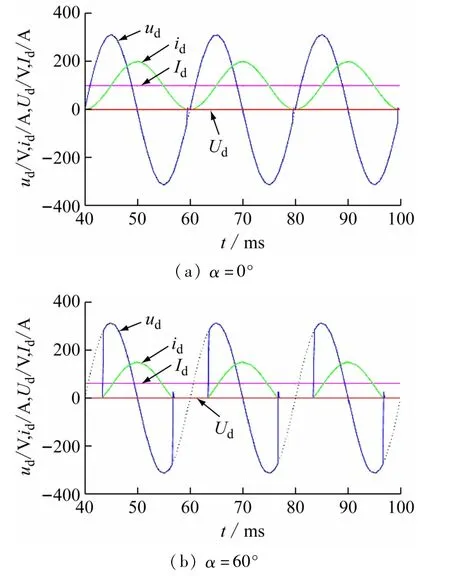
图5 不同控制角α时单相半波可控整流器的电压电流波形

与图4 纯电阻负载仿真波形相比，图5 中电感负载两端的输出电压ud出现了“负电压”部分，而且，在纯电感负载时，由于电感储能和释能时间基本一致，所以，不论控制角α ＝0°还是α ＝60°，电感负载两端的输出电压ud的正负半周的面积基本上是相同的，也就是说，电感负载两端的输出电压ud的平均值Ud＝0，为使整流器纯电感负载时输出电压不为零，一般需要在负载两端并联一个续流二极管，如图1（c）所示。从图5 还可以看出，随着控制角α 的增大，晶闸管VT 的导通时间越来越小，相应的负载电流id也会越来越小，在ud波形的正半周时，输出电压和负载电流的方向是一致的，相当于输入电源对电感充磁；在ud波形的负半周时，输出电压和负载电流的方向相反，电感释放之前储存的能量。而且在一个开关周期中，电感L 释放的能量等于储存的能量，二者实现能量的充、放电平衡，所以，单相半波可控整流器在纯电感负载时控制角的移相范围是：α∈（0°，180°）。当电源电压处于负半周时，由于感性负载的存在使得电流并没有立即减为零，因此晶闸管VT仍然处于导通状态，在这个过程中电感中存储的能量持续释放，直至能量全部耗尽，此时晶闸管VT关闭，电流降为零。随着控制角α的增大，电感在电压正半周时储存的能量减少，维持导电的能力就越弱，因此可能会导致电流出现断续状态。

将图5 所得仿真波形与前述理论分析相比较，可以看出：式（4）与图5（a）中仿真得到的输出电压ud的波形相吻合；式（7）与图5（b）中仿真得到的输出电压ud的波形相吻合。式（5）与图5（a）中仿真得到的负载电流id的波形相吻合，仿真得到的负载电流平均值经测量为98.20 A，式（6）的计算值为99.03 A，相对误差为0.84%；仿真得到的负载电流有效值经测量为120.58 A，式（7）的计算值为121.29 A，相对误差为0.95%。式（9）与图5（b）中仿真得到的负载电流id的波形相吻合，仿真得到的负载电流的平均值经测量为59.93 A，式（10）的计算值为60.31 A，相对误差为0.63%；仿真得到的负载电流的有效值经测量为82.84 A，式（11）的计算值为83.26 A，相对误差为0.50%。由此可知：理论计算值与仿真实验所得到的结果在误差范围内可以认为是一致的。

4 结 语

本文以单相半波可控整流器案例为研究对象，采用Simulink仿真工具，建立系统的电力电子仿真模型，分析了电阻负载工况下整流器的工作原理，借助仿真波形对比分析了在控制角α ＝0°、α ＝90°、α ＝120°时单相半波可控整流电路的输出电压和电流的工作状态，并与理论计算值进行了对比。研究了单相半波可控整流器纯电感负载，采用分段线性分析的方法，得出输出电压和电流的微分方程，给出了实例分析和相应输出电流的均值、有效值，仿真结果表明，在误差范围内所述理论与仿真结果一致。该仿真模型的建立，可培养学生分析、解决复杂感性负载电路的有关工程问题，同时提升学生仿真能力、探索与归纳总结能力、质疑探索等能力，引导学生积极参与、深入思考，活学活用电力电子技术相关知识。目前该案例分析在本科生和研究生的教学实践过程中已经应用并取得了良好的教学效果。