Spark下基于PCA和分层选择的随机森林算法

雷 晨，毛伊敏

江西理工大学 信息工程学院，江西 赣州 341000

随机森林算法是机器学习领域中的一种集成学习方法[1]，它通过集成多个决策树的分类效果来组成一个整体意义上的分类器。随机森林算法相比其他分类算法而言具有诸多优势，分类效果上的优势体现在分类准确度高、泛化误差小而且有能力处理高维数据，训练过程的优势体现在算法学习过程快速而且易于并行化。基于这两大优势，随机森林算法受到人们广泛关注。

随着互联网信息技术的不断发展以及大数据时代的到来，使得大数据相较于传统数据，具有了体积大（Volume）、种类多（Variety）、速度快（Velocity）、价值高（Value）的“4V”特性[2]。但是传统的随机森林算法所需的时间复杂度较高，只适用于较小规模的数据集，而在处理大数据时，无疑会产生巨额的计算复杂度[3]。所以，如何降低随机森林算法的计算复杂度，使其能处理大数据，是个关键性的难题。

近年来，随着Google公司开发的Spark架构的广泛应用，以Spark为代表的分布式计算架构受到了越来越多的关注[4-5]。为了进一步降低随机森林算法的计算复杂度，通过改进传统的随机森林算法，并与分布式计算架构相结合成为当前随机森林算法的研究热点。Wu等人[6]最早提出了大数据下基于Spark的可扩展随机森林算法，为解决随机森林算法处理大规模数据时，迭代频繁和性能较低的问题，该算法利用Spark框架实现了计算任务的缓存式执行，消除了迭代依赖，但是该算法在特征变换过程中未考虑到冗余特征过多所引起的协方差矩阵规模过大的问题，对此，Ahmad等人[7]在Spark框架下提出了一种基于知识约简的并行随机森林算法，使用粗糙集理论对数据集进行先压缩，后填补，降低非信息特征，提高了特征信息浓度；Bania等人[8]在基于优势关系的粗糙集模型的基础上，提出了基于相似优势关系的随机森林算法PRF，并将其基于Spark实现了并行化。虽然这些算法进行了一定的冗余特征剔除，压缩了特征集的规模，但是并没有完全解决协方差矩阵规模较大的问题。此外，这些算法在计算节点上构建特征子空间时，都是以均匀随机的方式选取特征，未考虑到分布式环境下子空间特征信息覆盖不足的问题。

如何解决子空间特征信息覆盖不足的问题，一直是并行随机森林算法的重要研究内容。为了处理这个问题，Galicia等人[9]提出了一种基于子空间加权选择的并行随机森林算法WECRF，在子空间选择过程中，给予低信息素特征较低的选择权重，降低其被选取的概率；Lulli等人[10]提出一种Spark环境下基于子空间分层选择的并行随机森林算法DRF，应用一个统计准则把特征分为三个部分，然后，使用分层抽样的方式构造特征子空间。虽然这些算法都对均匀选取特征子空间的方式进行了改进，但是没有完全解决子空间特征信息覆盖不足的问题。除此之外，这些算法都未考虑并行化训练决策树的过程中，由于特征信息利用率过低，引起节点通信开销过大的问题，于是，Morfino等人[11]在Spark环境下提出了一种数据并行化的随机森林算法Spark-MLRF，设计了一种RDD数据划分策略并结合分区采样的方式来减少数据的传输操作，但是由于其使用的是水平划分方式，虽然减少了局部通信频率，但全局通信开销并未降低，而且该算法随着森林规模k的继续增大，训练决策树时的数据通信过程的操作量会呈线性增加，并未从根本上解决决策树训练过程中通信开销大的问题。

针对上述三个问题，本文提出了基于PCA和分层抽样的并行随机森林算法PLA-PRF（PCA and subspace layer sampling on Parallel random forest algorithm），主要贡献如下：（1）提出了“MFS”策略获取主成分特征，有效避免了特征变换过程中协方差矩阵规模较大的问题；（2）提出了“EHSCA”策略，将所获得的主成分特征进行分层选择，解决子空间特征信息覆盖不足的问题；（3）在Spark环境下训练决策树的过程中，设计了数据复用策略“DRS”，提高分布式环境中的特征利用率，有效降低了分布式环境下决策树训练过程中的节点通信开销，实验结果表明，PLA-PRF算法的分类效果更佳。

1 相关技术介绍

1.1 分布式计算平台—Spark

Spark是一种基于内存的分布式计算平台[12]，旨在简化集群上并行程序的编写，Spark继承了MapReduce的线性扩展性和容错性，同时也改进了MapReduce必须先映射（Map），再规约（Reduce）的串行机制，Spark通过有向无环图（directed acyclic graph，DAG）算子将中间结果直接移交给作业的下一阶段，所有中间过程都是在内存中进行缓存，不必像MapReduce那样每次迭代都要从磁盘重新加载数据。在Spark中，核心抽象概念就是弹性分布式数据对象RDD（resilient distributed datasets），Spark中计算任务的组织、运算、调度、错误恢复都是以RDD为单元进行的，Spark的任务工作流如图1所示。

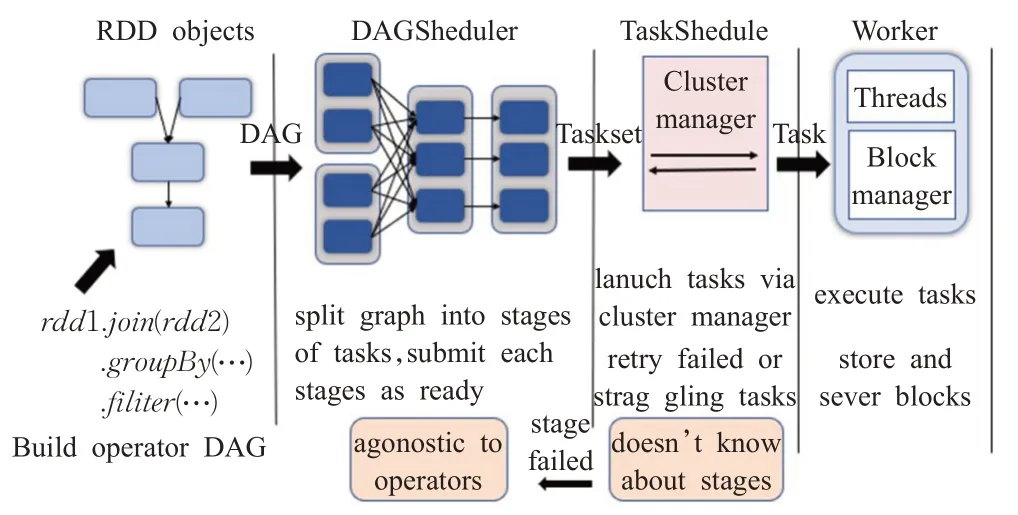
图1 Spark的任务调度流程图Fig.1 Spark task scheduling flowchart

在图1中，各个RDD之间存在着依赖关系，通过这些依赖关系形成有向无环图DAG；DAGshedule负责将DAG作业分解成多个Stage，每个Stage则根据RDD的Partition个数决定Task的个数，然后生成相应的TaskSet交给TaskShedule容器，TaskShedule容器负责将Task发送给clusterManager进行任务监测和加载，随后将其交由worker线程池调度执行，若执行失败，则重新加载，并将失败日志返回给DAGshedule。

1.2 PCA

主成分分析（principal component analysis，PCA）[13]是一种将原有的多个变量通过线性变换转换为少数综合变量的统计分析方法，其基本数学原理如下：

设n维向量w是低维映射空间的一个映射向量，则经过最大化数据映射后其方差公式如下：

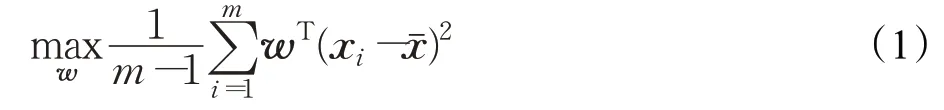
式（1）中m是参与降维的数据个数，xi是随机数据i的具体向量表达，xˉ是所有参与降维的数据的平均向量。

假定W是由包含所有特征映射向量的列向量所组成的矩阵，该矩阵可以较好地保留数据中的信息，该矩阵经过代数的线性变换可以得到一个优化的目标函数如下：

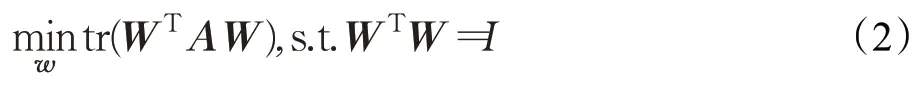
式（2）中tr是矩阵的迹，A是协方差矩阵，表达式如下：

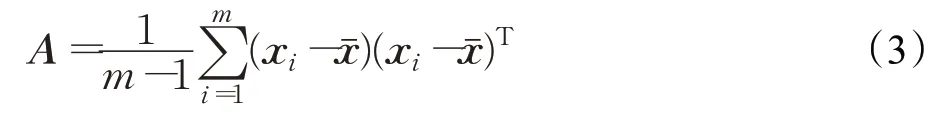
PCA的输出：Y=W′X，最优的W是由协方差矩阵中前k个最大的特征值所对应的特征向量作为列向量构成，通过该过程将X的原始维度降低到了k维。

1.3 误差约束分层

定义1（误差约束分层）[14]假定数据源为d(d有 ||d个元组和n个属性A={A1,A2,…,An})、分层属性集合Φ∈A。在d的所有元组中，d(Φ)为属性集合Φ上不同值x的集合，且对应于每个x都有d中的元组集合d(x)={t:t∈d且t在属性集合Φ上取值为x}，记d中属性集Φ上分组数量为 ||d(Φ)。给定相对误差ε＞0，从d中选择样本S(d)⊆d，对每个具体的层次d(x)，存在对应的样本集合Sx(d)⊆S(d)为d(x)的子集。

1.4 KD树

KD树[15]被定义为一棵节点均为k维向量的二叉树，是一种用于分割k维数据空间的数据结构。KD树的所有非叶子节点均可以视作一个超平面，该超平面可以将空间中的数据分成两个部分，通过选定k维数据中的某一维度，并按照左小右大的方式来划分数据，落在超平面左侧的点被分到结点的左子树上，右侧的点则被分到节点的右子树上。

2 PLA-PRF算法

2.1 算法思想

PLA-PRF算法主要包括三个阶段：特征变换、子空间选择和并行训练决策树。（1）在特征变换阶段：提出“MFS”策略，使用特征矩阵分解方程“CMDE”（characteristic matrix decomposition equation）降低协方差矩阵的计算代价，获得变换后的主分成特征，有效避免了协方差矩阵规模过大的问题；（2）在子空间选择阶段：提出“EHSCA”策略，使用误差约束公式“ECF”（error constraint formula）对主成分特征进行分层选择，提高子空间特征信息覆盖度；（3）并行训练决策树阶段：在Spark环境下设计了一种RDD数据复用策略“DRS”，垂直划分RDD数据并将其索引保存在DSI（data search index）表中，实现特征信息的重复利用，降低节点通信开销。

2.2 特征变换

目前，基于特征子空间改进的并行随机森林算法通常采用主成分分析法进行特征变换，然而该方法在面对冗余特征过多的大数据集时，存在协方差矩阵规模较大的问题。针对这一问题，提出了“MFS”策略，压缩原始特征集，解决协方差矩阵规模较大的问题。“MFS”策略如下：

（1）对于原始数据集D={(Xi,Yi),Xi∈ℝD,Yi∈y}Ni=1,使用Bootstrap抽样算法[16]获得训练子集Dm(m=1,2,…,M)的特征集F,并将F划分为L个特征子集F(l)(l=1,2,…,L)。

（2）使用公式（3）构造F(l)的协方差矩阵S，并计算S的特征矩阵A,提出特征矩阵分解方程“CMDE”（characteristic matrix decomposition equation）对A进行分解。

定义2（特征矩阵分解方程CMDE）。若矩阵A是一个N×F(l)的实数矩阵，其中N表示样本个数，F(l)表示特征数，UN×N和VF(l)×F(l)均为单位正交阵，Σ仅在主对角线上有值(σ)，且维度分别为U∈RN×N,Σ∈RN×F(l),V∈RF(l)×F(l),则特征矩阵A分解方程如下所示：

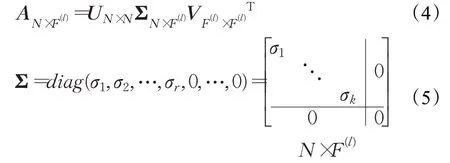
证明设，存在m×n的矩阵A且存在一组正交基，使得经过矩阵A分解变换后还是正交的，这组正交基为{v1,v2,…,vn}。

其中，V表示ATA所分解出的特征向量矩阵，ΣTΣ是ATA的特征值矩阵，当特征值λi越小，其所对应的特征向量ui对分类的重要性越低，λi被剔除的可能性越高，反之，被剔除的可能越低。

（4）最后，按照特征值{}λ将特征向量{}u由大到小排序，在满足算法预期性能的情况下，对特征值较低的特征向量进行剔除，得到特征子集F′(l)，统计所有特征子集，得到变换后的主成分特征

2.3 子空间选择

目前，基于特征子空间改进的并行随机森林算法，通常采用随机均匀的方式构建特征子空间，然而该方式未考虑特征间的信息差异，这导致子空间特征信息覆盖不足，针对此问题，基于主成分特征D(l)m′，设计了“EHSCA”策略，分层选取特征子空间，提高子空间特征信息覆盖度。“EHSCA”策略如下：

（1）根据特征分割参数R，将主成分特征集D(l)m′的前r个特征分配给高信息素空间A1，将后F(l)-r个特征分配给低信息素空间A2，特征分割参数定义如下：

（3）分别从A1和A2中抽取特征，提出误差约束公式“ECF”（error constraint formula）确定在A1和A2中抽取的特征数量，误差约束公式定义如下：

定义4（误差约束公式ECF）。若NA1和NA2分别表示是来自两个层次A1和A2的特征样本数量，δ表示给定置信度，ε代表查询Q(d(x))的误差，则误差约束公式“ECF”如下所示：

（4）根据NA1和NA2分别在层次A1和A2中进行随机抽样，得到包含所有信息的特征子空间。

使用“EHSCA”策略构建特征子空间的伪代码如算法1所示：

2.4 并行训练决策树

目前，在Spark环境下，基于特征子空间改进的并行随机森林算法虽然保证了分类准率，但是这些算法在并行化训练决策树的过程中未考虑到分布式环境中的数据量会随森林规模增大而线性增加[18]，使得特征信息利用率较低，进而导致节点通信开销大的问题，针对此问题，本文在并行化训练决策树的过程中设计RDD数据复用策略“DRS”，通过垂直划分RDD数据并结合索引表，实现数据复用，降低了节点通信开销，“DRS”策略如下：

（1）根据RDD特征空间构建KD树，根节点指向整个特征空间并存放所有的数据记录N,每个叶子节点记录划分后的输入特征变量以及输入特征变量所包含的特征属性yi，选取数据空间离散系数（coefficient of variation，CV）[19]最大的维度作为KD树的划分维度d，该维度下的数据均值作为KD树的分割节点w，根据d和w提出划分准则函数（partition criterion function，PCF），其定义如下：

定义5（划分准则函数PCF）。若RDD数据中第i维度下的均方差为Si，均值为μ，KD树中划分维度d下的记录个数为num，则PCF函数计算如下：

（2）使用“PCF”函数获取KD树的分割维度和划分节点后，对当前空间数据进行判断，若数据在当前分割维度d中小于分割节点w，则将此数据yi与目标特征yM-1链接作为一个垂直数据块RDDFSJ，否则继续遍历KD树。重复此过程，直到划分出(M-1)个数据分区R DDFSjj∈[0,M-2]，M为Slave节点数量，划分过程如图2所示。

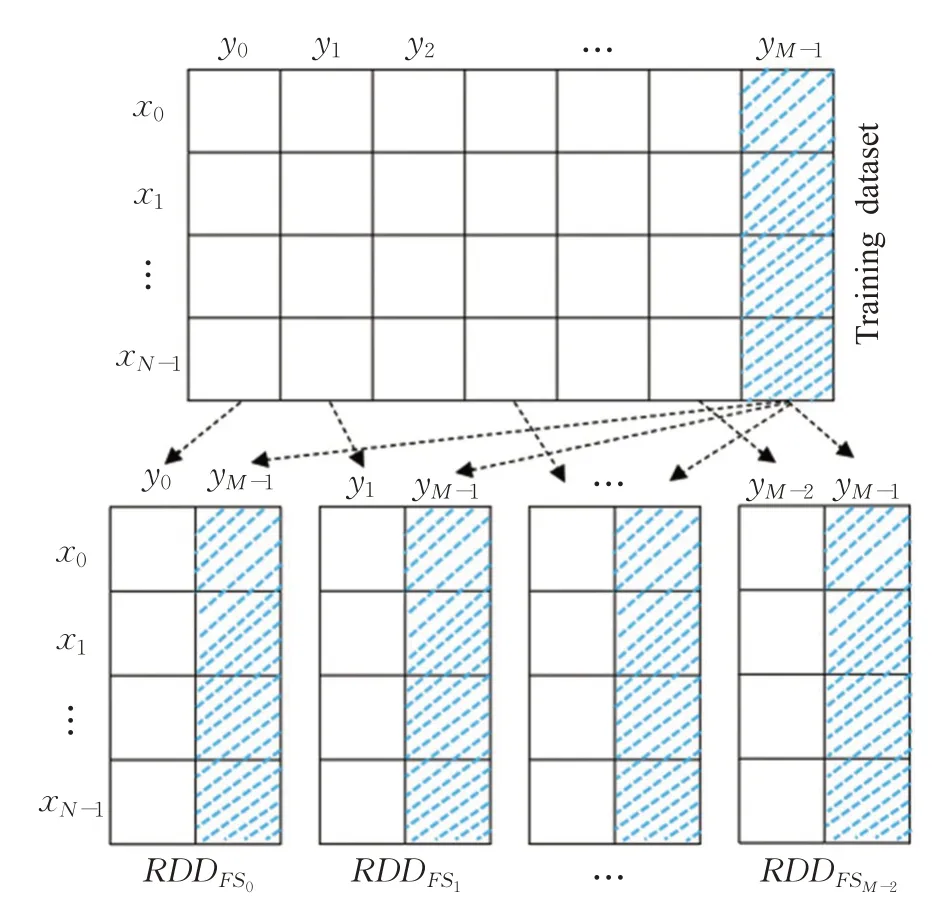
图2 垂直数据划分Fig.2 Vertical data partition

（3）完成RDD数据对象垂直划分后，将这些RDDFS特征子集发送给分布式Spark集群中的各slave，并通过dataAllocation( )和persisit( )函数存储在Spark集群中。接着，在每个slave中创建一个DSI表存储采样过程中生成的数据索引，例如：若森林规模为k，则对于训练数据集，存在k个采样周期，并且在每个采样周期中都会记录下N个数据索引，形成k行N列的DIS索引表，如表1所示。

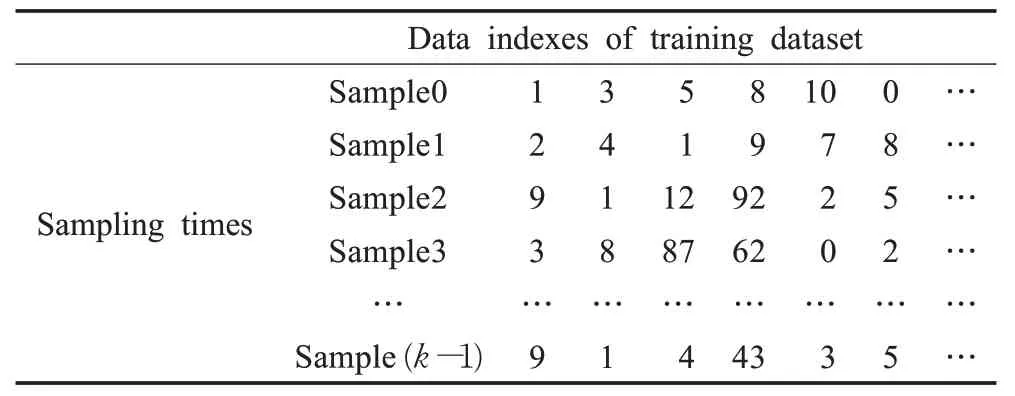
表1 DSI索引表Table 1 DSI index table

（4）每棵决策树训练过程中所需的计算任务都通过DSI表从同一特征子集RDDFS中加载相应的数据，例如：在增益比计算过程中，每个增益比计算任务都会访问DIS表以获得相关索引，并根据索引从同一特征子集中获得特征记录，从而快速的访问特征子集，进行决策树分裂，完成决策树并行训练，具体过程如图3所示。

图3中每个TGR代表增益比计算任务，首先，根据特征子集RDDFS1、RD DFS2、RDDFS3分别向Slave站点中分配增益计算任务{TGR1.1,TGR1.2,TGR1.3}、{TGR2.1,TGR2.2,TGR2.3}、{TGR3.1,TGR3.2,TGR3.3}每个站点中的增益计算任务分别属于Decisi onTree1、DecisionTree2、DecisionTree3；其次，根据TGR需求，通过DSI索引从RDDFS特征子集中获取特征记录，为决策树计算特征变量的增益比；最后，使用{TGR1.1,TGR2.1,TGR3.1}进行DecisionTree1的节点拆分，使用{TGR1.2,TGR2.2,TGR3.2}和{TGR3.1,TGR3.2,TGR3.3}分别进行DecisionTree2和DecisionTree3的拆分。

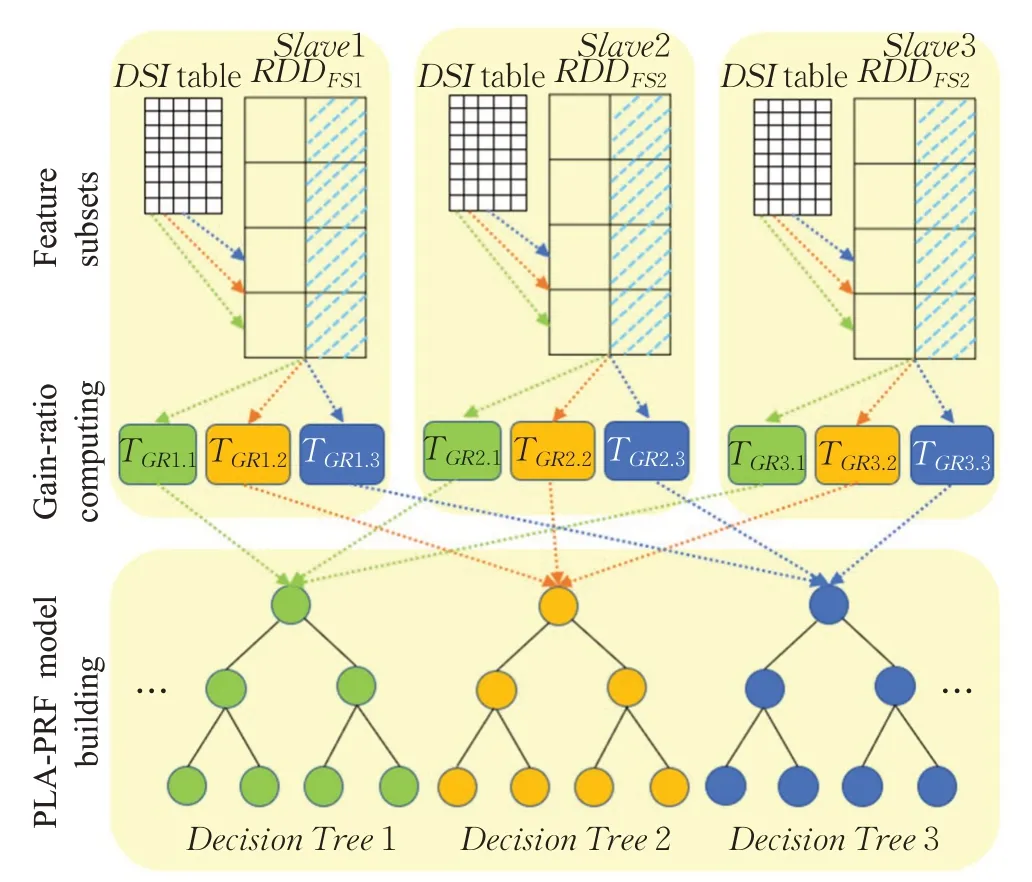
图3 决策树并行训练过程Fig.3 Decision tree parallel training process

决策树并行训练过程的伪代码如算法2所示：

2.5 PLA-PRF算法步骤

PLA-PRF算法的具体实现步骤如下所示：

步骤1输入原始数据，将其划分成大小相同的RDD数据块；对于每个RDD数据块的特征集，调用“MFS”策略进行特征变换，剔除冗余特征，获得主成分特征，将其存入每个任务节点。

步骤2根据“EHSCA”算法在主成分特征中进行子空间分层选择，生成特征子空间。

步骤3依据特征子空间，使用“DRS”策略并行训练决策树，生成相应的DAG任务，最后，将DAG中的任务提交给Spark的任务调度程序以完成所有模型训练。

2.6 时间复杂度分析

PLA-PRF算法的时间复杂度主要由特征变换、子空间选择、决策树并行化训练这几个步骤组成，分别记为T1、T2、T3。

特征变换阶段时间花销主要体现在协方差矩阵的计算中，假设预训练样本数为n，特征数量为m，则特征变换的时间复杂度为：

在子空间选择阶段，假设节点数为a，“EHSCA”算法的每一次误差约束计算都要查询一次当前数据库中的某个特征属性值，假设在完成n次迭代后，达到指定置信度δ，则子空间选择的时间复杂度为：

在决策树并行化训练阶段，其时间复杂度主要取决于TGR（增益比计算）任务和TNS（节点拆分）任务的计算时间，分别表示为TG和TN，假设决策树数量为k，则增益比计算任务的时间复杂度为：

由于大数据环境下训练RF时T3≫T1和T2，而且通过数据复用技术直接提升了分布式环境中的数据利用率，即T3-Spark-MLRF≫T3-PLA-PRF，因此PLA-PRF算法时间复杂度远低于算法Spark-MLRF。

3 实验结果以及分析

3.1 实验环境

为了验证PLA-PRF算法的分类性能，本文设计了相关实验。硬件方面：所有的实验都在Atlas（Atlas-2.2.1.el6.x86_64.rpm）研究组集群中进行，该集群由12节点组成，每个节点有2个Inter E5-2620微处理器（2 GHz，15 MB缓存）和64 MB主存，1 Gb/s的以太网链接。在软件方面，每个节点安装的操作系统为Ubuntu 18.04，Spark架构为Spark-Scala-Intellij，软件编程环境为Java JDK 1.8.0。节点具体配置情况如表2所示。

表2 节点基本配置表Table 2 Basic node configuration

3.2 数据来源

PLA-PRF算法采用的实验数据为四个来自UCI公共数据库的真实数据集（http：//www.ics.uci.edu/～mlearn/MLRepository.html），分别是URL Reputation（URL）、You Tube Video Games（Games）、Bag of Words（Words）和Gas sensor arrays（Gas）。URL是模式识别文献中最著名的数据集，包含924 472条数据，具有数据量小等特点；Games是从IT公司使用的ServiceNowTM平台实例的审计系统收集的数据，该数据集有3 013 883条实例，具有多元、记录长度长等特点；Words是一组有关粒子加速器探测粒子的数据，该数据集有5 000 000条记录，具有数据量大，数据均匀等特点；Gas包含11 000 000条数据，具有数据量大，数据离散等特点。数据集的详细信息如表3所示。

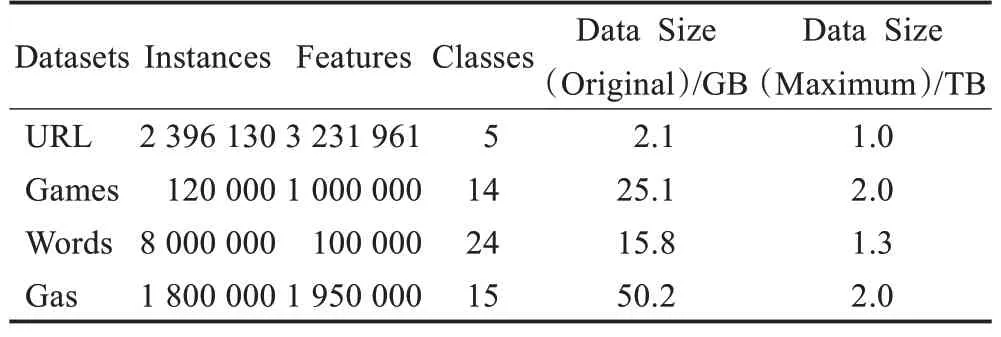
表3 UCI机器学习库中数据集Table 3 Datasets from UCI machine learning repository

3.3 评价指标

本文采用Kappa系数作为指标来衡量算法对大数据集的分类准确率[20]。假设每一类真实样本的个数分别为a1,a2,…,ac，而预测出来的每一类样本个数分别为b1,b2,…,bc，总样本个数为n，则Kappa系数计算方式如下：

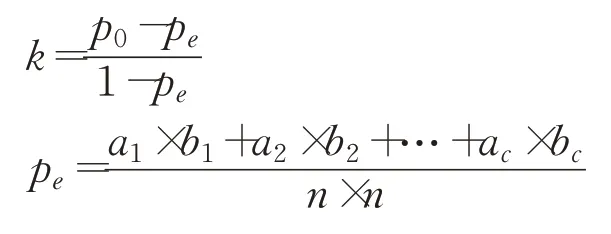
其中，p0表示总体分类精度。通常情况下，k值落在0～1之间，可分为5组来表示不同的一致性级别，一致性越高，表示分类准确率越高，如表4所示。

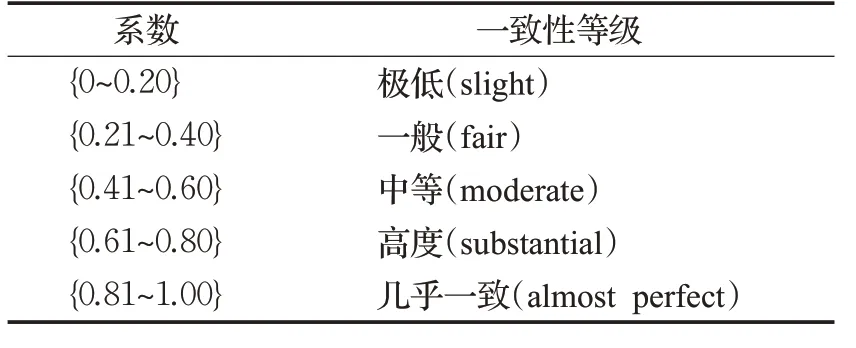
表4 一致性级别表Table 4 Consistency level table

3.4 算法的分类准确率分析

3.4.1 不同森林规模下的算法准确率分析

为验证PLA-PRF算法的分类准确率，本文使用URL数据集进行对比实验，根据算法在不同决策树规模下的平均分类精度与PRF[8]、DRF[10]、Spark-MLRF[11]算法进行综合比较。实验结果如图4所示。

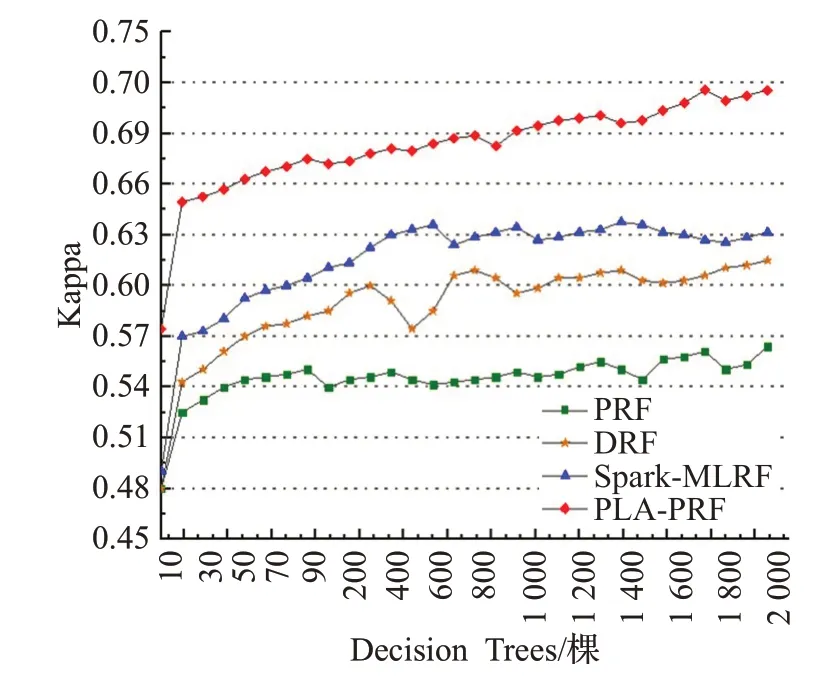
图4 各算法在不同森林规模下的平均分类准确率Fig.4 Average classification accuracy of each algorithm under different forest scales

从图4可以看出，当决策树的数量等于10时，所有比较算法的平均分类精度都较低，随着决策树数量的增加，这些算法的平均分类精度逐渐呈波动型增加，当决策树数量增加到1 300时，与PRF和DRF算法相比，PLA-PRF算法的平均分类精度高出大约6.1%和10.6%，当决策树数量达到1 500时，PLA-PRF算法比Spark-MLRF的分类准确率高约4.6%，可以看出，随着决策树规模的增加，PLA-PRF算法的精度增益明显高于其他三个算法，这是因为PLA-PRF算法使用“EHSCA”策略提升了子空间特征信息覆盖度，从而提高了分类准确率，因此可以得出结论，在森林规模较大的情况下，PLA-PRF算法精度最高。

3.4.2 不同数据集下的算法准确率分析

为验证PLA-PRF算法在不同数据集下的分类准确率，本文分别在四个数据集上进行实验，根据Kappa值，分别与PRF、DRF算法和Spark-MLRF算法进行综合比较，实验结果如图5所示。

从图5中可以看到，相比于DRF算法，PLA-PRF、Spark-MLRF和PRF算法在四个数据集上表现较好，Kappa值分别平均提升约3.13%、2.56%和1.98%，而DRF算法在样本规模较少的情况下，分类准确率较高，而随着样本规模的增加，分类精度逐渐降低，是因为该算法在子空间构建过程中，舍弃了一些高信息素特征，使得特征新空间信息不足，导致决策树训练过程中未学习到被抛弃的数据内在规律。从URL、Games和Words中可以看出，在特征数量较少且复杂度较低数据集上，Spark-MLRF算法表现略优于PLA-PRF和PRF算法，而在特征数量较多的数据集Gas上，PLA-PRF算法的平均准确率比Spark-MLRF和PRF分别高3.1%和5.9%，而在样本规模达到65 000时，PLA-PRF分类准确率要高出8.9%和15.6%。这是因为，PRF算法在子空间构造过程中使用了维度缩减算法，虽然保留了主要成分特征的，但是在后续的子空间选择时并没有进行分层抽取，导致特征子空间信息不均，在面对特征较多的大数据集时，随着数据划分次数的增加，训练子集的信息缺失越发严重，进而降低了分类准确率；Spark-MLRF算法虽然通过分层抽取的方式一定程度上解决了PRF的子空间信息缺失问题，但由于其对每个分区都进行单独采样，随着数据集规模的增大，数据集的随机选择比例增加，分类准确率有所下降；而PLA-PRF算法使用了“EHSCA”策略进行子空间选择，充分保证了特征子空间的信息覆盖度，最终提高了模型的分类准确率。综上所述，可得，PLA-PRF算法适用于处理规模较大，特征复杂数据集。

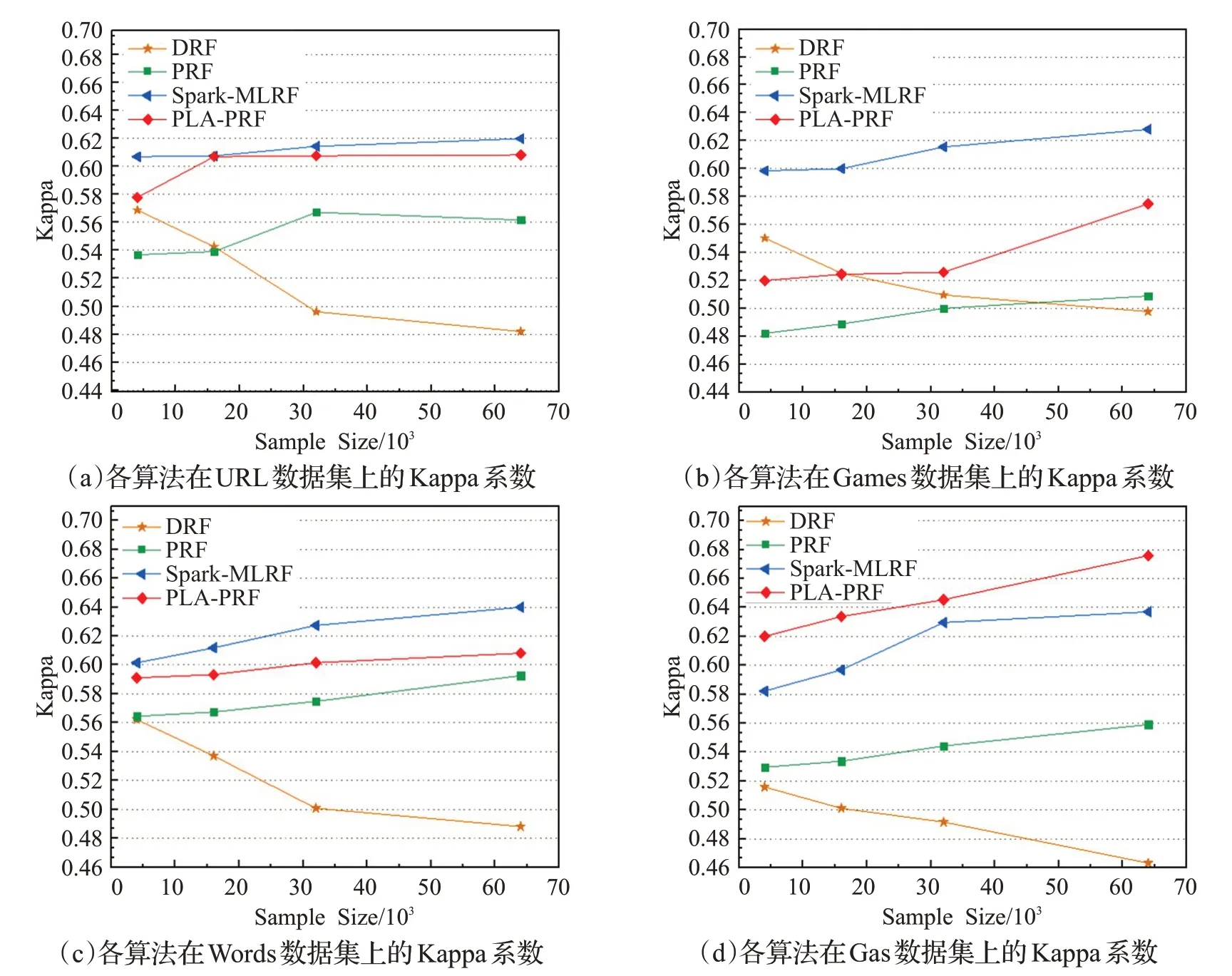
图5 各算法在四个数据集上的平均分类精度Fig.5 Average classification accuracy of each algorithm on four data sets

3.5 算法性能比较

为验证PLA-PRF算法的性能，本文与Spark-MLRF和DRF算法进行对照实验，实验中使用了4组数据集（URL、Games、Words、Gas），每种算法在实验过程中，决策树规模均设定为500，Spark站点数量设置为10，实验结果如图6所示。

图6为PLA-PRF、Spark-MLRF和DRF算法在四个数据集上的执行结果。从图中可以看出，当数据规模小于1 GB时，PLA-PRF和Spark-MLRF算法执行时间比DRF长，平均约为DRF的138%，原因是将算法提交到Spark集群并配置程序需要固定的时间，在数据量较小时，该时间在算法运行时间中所占比重较大，但是当数据量从1 GB增长到500 GB时，DRF的平均执行时间从19.9 s增长到517.8 s，而Spark-MLRF的平均执行时间从24.8 s增加到186.2 s，PLA-PRF的平均执行时间从23.5 s增加到101.3 s。由此，可以看出，在大数据集下PLA-PRF与Spark-MLRF和DRF相比具有更快的执行速度，而且随着数据量的增大，优势更加明显，这是因为PLA-PRF在并行化的过程中使用了数据复用策略“DRS”，减少了分布式环境中的数据通信开销，提升了算法的并行化效率。

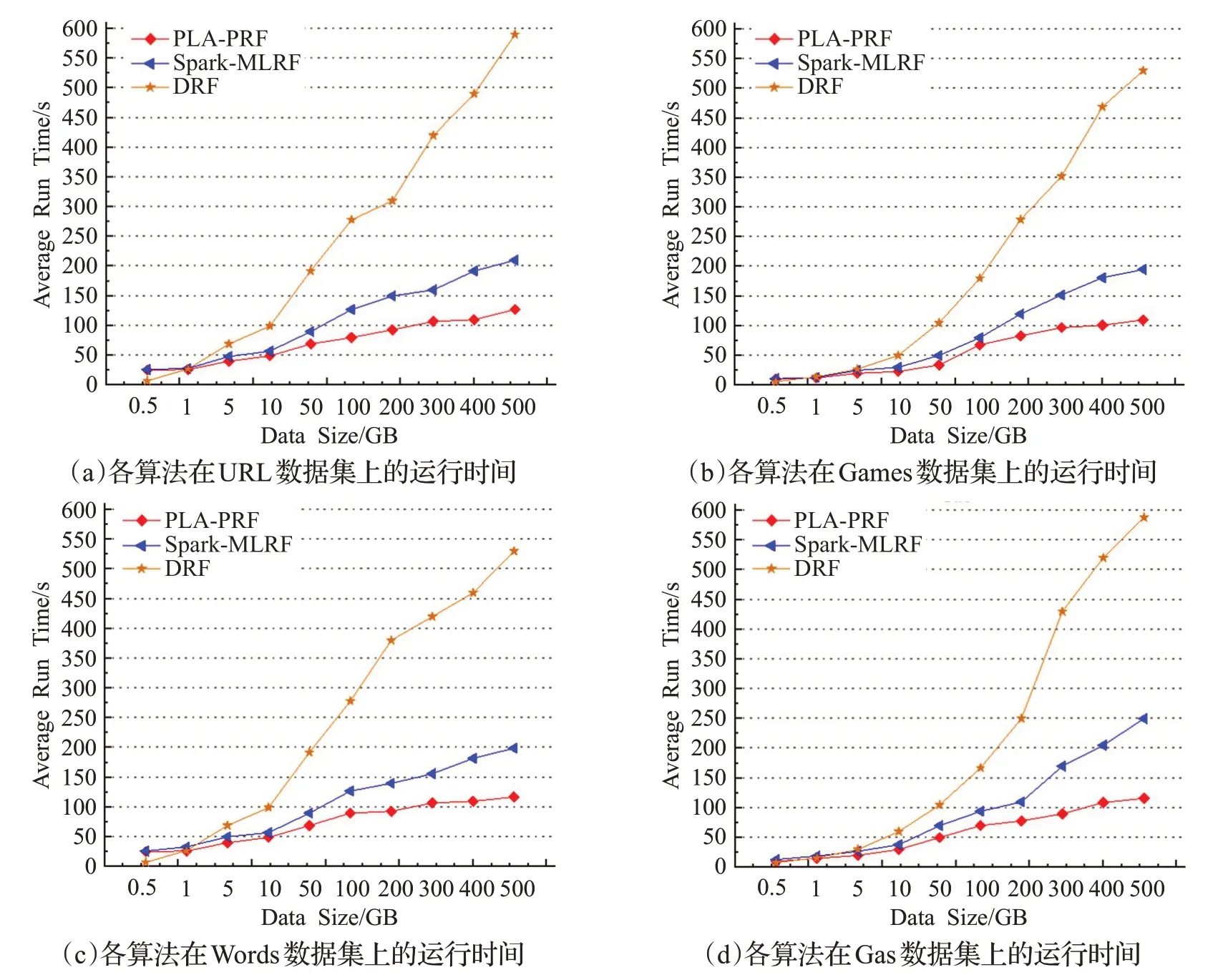
图6 各算法在四个数据集上的平均运行时间Fig.6 Average running time of each algorithm on four data sets

4 结语

为解决传统随机森林算法在大数据环境下，分类结果准确率低，并行化效率差的问题，本文提出了一种基于PCA和分层子空间抽样的并行随机森林算法。面对并行随机森林算法在特征变换过程中协方差矩阵过大的问题，提出一种基于PCA的特征变换方法，接着，对于所得主成分特征，提出了一种误差约束的分层子空间构造算法，优化特征子空间，解决子空间特征信息覆盖不足的问题。最后，在Spark环境下并行化训练决策树的过程中，设计了一种数据复用技术，有效减少了分布式环境中的节点通信开销，提高了并行效率。实验结果表明，在数据规模较大且特征维度较高的情况下，本文算法可以更高效地完成分类过程。虽然PLA-PRF算法在分类准确率和并行效率方面取得一些进步，但依然存在一定的提升空间，一方面，在特征变换过程中能否适当引入群智能算法来优化原始特征集，提高特征集的寻优精度；另一方面，在处理集群计算任务时，Spark平台的TaskScheduler模块会根据不同的任务资源需求使用不同的调度方式，因此，在调度DAG的过程中，可以考虑对信息增益任务和节点拆分任务分别给出不同的调度策略，从而进一步提高算法的资源利用率，提升并行效率，这些将是本文今后的重点研究内容。