长板短桩复合地基的固结解析解

江培兵

(1. 中国地质大学 工程学院， 武汉 430074； 2. 中铁第四勘察设计院集团有限公司， 武汉 430063)

1 计算模型与基本假定

1) 桩体为不透水桩，不存在超静孔隙水压力.

2) 等应变条件成立，桩体、土体和竖井仅发生竖向变形，土体和竖井的压缩模量相等.

3) 土中既有竖向渗流也有径向渗流，竖井中仅有竖向渗流，且渗流服从Darcy定律.

4) 外部荷载p(t)是时间的函数，表达式为p(t)=pug(t)，其中，pu为外部荷载的最大值，g(t)为描述加载过程的时间函数.

5) 土体的竖向渗透系数kv保持不变，水平方向扰动区和未扰动区的渗透系数kh也保持不变，如图2所示，其表达式为

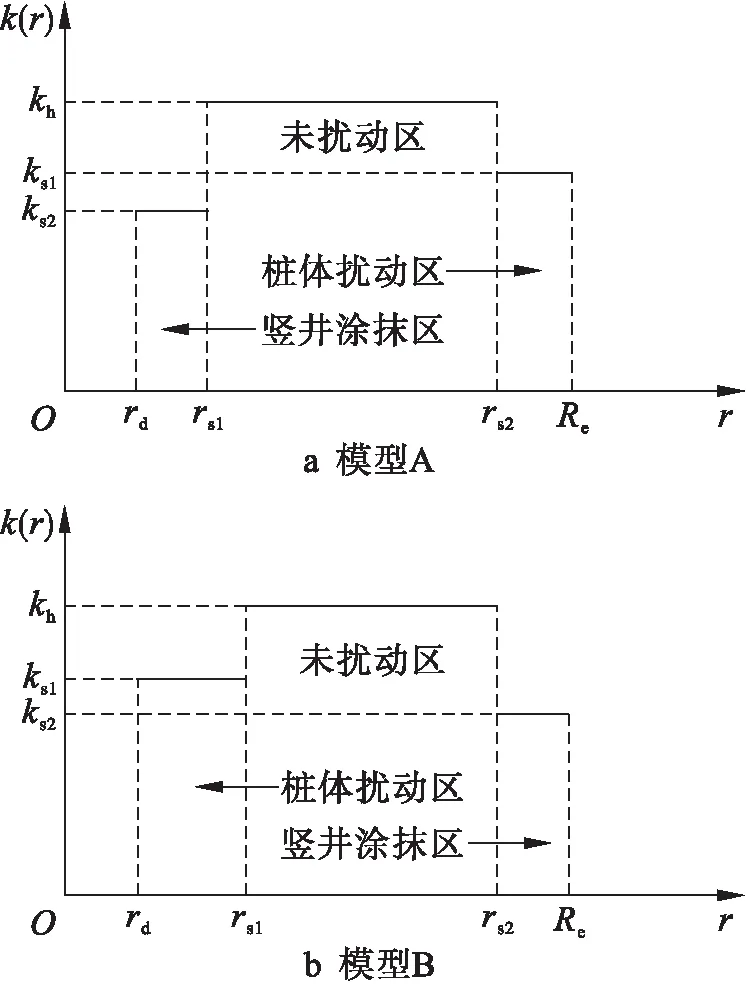
图2 两种模型中桩体和砂井的扰动区

k(r)=khf(r)

(1)

式中，f(r)为关于砂井半径r的函数.

6) 任一时刻从土体流入竖井的水量与从竖井中流出水量之差等于竖井的体积变化量.

对于图1中的模型A和模型B，由平衡条件则有

图1 两种解析模型

(2)

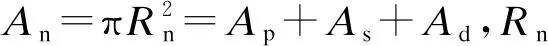
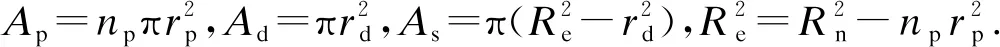
式中：Re、rp、rd分别为土体外半径、桩体和竖井半径.

由等应变假设可知：

(3)

由式(2)～(3)可得

(4)

(5)

(6)

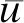
土体的轴对称固结方程统一表示为

(7)

式中：γw为水的重度；us为土体内任一点处的超静孔压.

上述平衡方程、等应变方程和固结方程对于模型A和模型B均成立，本文将根据模型A和模型B各自的特点分别求解.

2 固结方程及其求解

2.1 模型A固结方程

对于模型A，搅拌桩位于外围且不透水，竖井和土体界面的孔压相等，边界条件为

(8)

(9)

图3为dz厚度的竖井内水量变化和体积变化的关系，任意dt时间段内竖井内的竖向渗流量QV和从竖井周围土体流入竖井的水量Qhs分别为

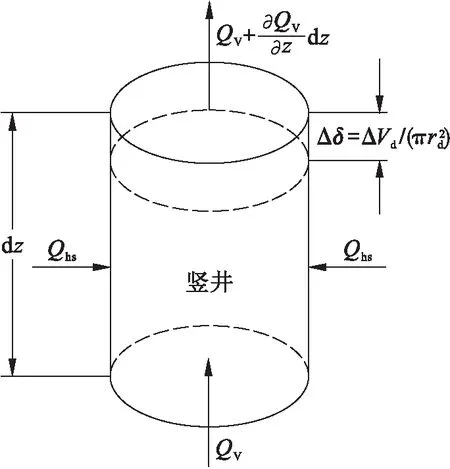
图3 竖井内水量变化和体积变化的关系

(10)

(11)

式中，kd为砂井的渗透系数.则在dt时间段内竖井内水量的变化量为

(12)

竖井的体积变化量(压缩)可表示为

(13)

根据式(6)、(12)和(13)可得

(14)

土体中任一深度处的径向平均孔压可表示为

碱洗过程控制液固比为10∶1，反应时间为1 h以上。碱洗完成后转化为黄色氧化铋，体积缩小，浆液变稀，Bi含量达到79.45%，可再进行酸化激活重复利用。

(15)

对式(7)关于r积分并联立式(8)和(1)可得

(16)

对式(16)关于r积分并联立式(9)可得

(17)

式中，

(18)

将式(17)代入式(15)后整理可得

(19)

式中，Fc为一个反应地基单元的几何特性和桩井扰动效应的综合参数.

联立式(14)和(16)可得

(20)

式中，Ned=Re/rd.由式(4)可得

(21)

由式(6)可得

(22)

(23)

将式(21)、(23)和(20)联立，可得

(24)

将式(20)、(22)和(19)联立，可得

(25)

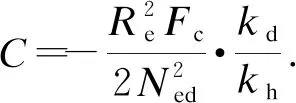
(26)

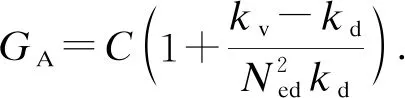
在式(26)中分别对t求一阶偏导，对z求二阶偏导，再联立式(24)，可得

(27)

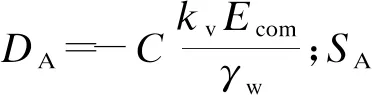
式(26)、(27)即为模型A的控制方程.

2.2 模型B固结方程

对于模型B，桩体位于单元中心，边界条件为

(28)

(29)

参考图3的推导过程，dt时间段内竖井的水量与竖井体积变化的关系为

(30)

土体中任一深度处的平均孔隙水压力为

(31)

计算过程与模型A一致，最终计算可得

(32)

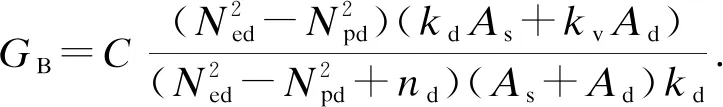
(33)

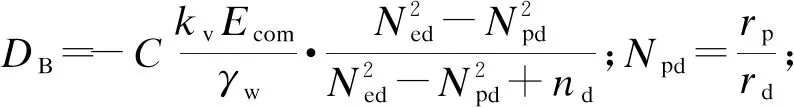
式(32)、(33)即为模型B的控制方程.

2.3 孔压及固结度解析解

在初始时刻，外部荷载由地基单元内的平均孔压承担，初始条件为

(34)

假设复合地基顶面排水，底面不排水，则竖向边界条件为

(35)

(36)

式中，

(37)

由于考虑了桩、土的共同作用，所以任意时刻复合地基按应力定义的总平均固结度为

(38)

3 实例验证

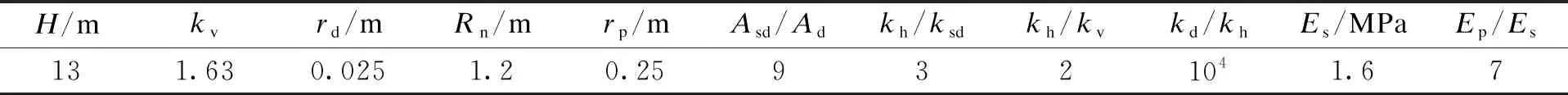
表1 试验参数

图4 三种模型对比

由图4可以看出，本文解与实测值的吻合度较高，说明本文解能较好地反映实际固结情况，也验证了本文解的合理性.但模型B的固结度总是大于模型A的固结度，本文假设模型A和模型B的计算值与卢萌盟解相比差距很小，尤其是模型A二者几乎重合.这是参数特定取值得到的结果，具有特殊性，无法区分本模型与卢萌盟解的区别，因此有必要对本文解和卢萌盟解的固结性状进行分析.

4 固结性状分析

表2 计算参数取值

在瞬时荷载pu保持不变的条件下，式(38)可化简为

(39)

4.1 井径比影响

图5为不同井径比时模型A和模型B的对比，其中，Th为复合地基径向时间因子.由图5可知，模型A和模型B在同一井径比时固结度存在的差距较小，模型B固结快于模型A，但差距随着时间因子和rp/rd值的增大而减小，模型A和模型B的固结速率随着搅拌桩与竖井的直径比增大而大幅度增大.因此，井径比rp/rd的取值对复合地基的固结度有显著影响，增大搅拌桩的桩径会减小排水路径，从而加快地基的排水固结.以模型A为例，rp/rd=10与rp/rd=4情况下二者的固结度差值最大超过30%，而rp/rd=14与rp/rd=10情况下二者的固结度最大超过20%.

图5 不同井径比时模型A和模型B的对比

图6、7分别为不同井径比时模型A和模型B与卢萌盟解的对比.从图6、7可以发现，模型A和模型B的卢萌盟解同样随着rp/rd的增大而大幅度增大，本文解慢于卢萌盟解，rp/rd值较小时差距不明显，但随着井径比增大，差距逐渐增大.本文解与卢萌盟解仅在竖井的水量这一假设条件上不同，实际工作中流入和流出排水板的水量总是存在差值，不存在相等的情况，因此，本文解优于卢萌盟解，固结度更适用实际情况，结果更加精确.

图6 不同井径比时模型A和卢萌盟解的对比

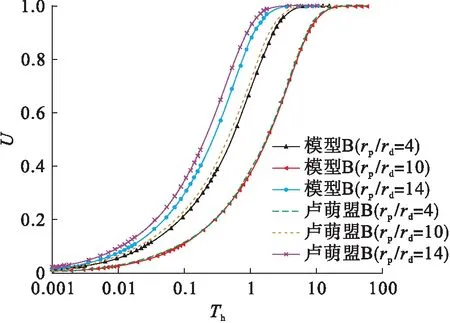
图7 不同井径比时模型B和卢萌盟解的对比

4.2 桩井扰动效应影响

图8为桩体扰动区渗透系数影响对比.从图8可以看出，当扰动区土体的渗透系数增大时，模型A和模型B的固结速率并没有明显提高，二者曲线几乎重合，模型B的固结速率在前期比模型A快约3%.由此可见，搅拌桩扰动区土体的渗透系数对地基土的固结无明显影响.事实上，由于将搅拌桩视为不透水桩，且距离竖井较远，因此，其扰动效应对地基排水的影响不明显.

图8 桩体扰动区渗透系数影响对比

图9为模型A竖井扰动区渗透系数对固结的影响.从图9可以看出，本文解和卢萌盟解都随着竖井扰动区渗透系数的增大而增大，ksd/kh=0.1与ksd/kh=1相比，二种解的固结度差值最大超过4%，所以竖井扰动区渗透系数对固结度有着较大影响.尽管塑料排水板等效为竖井的直径很小(本文取rd=25 mm)，但仍使竖井的扰动区土体渗透系数变小，所以本文得到的计算结果将更精确.

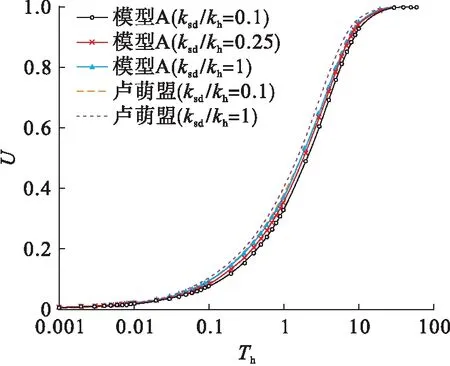
图9 模型A竖井扰动区渗透系数对固结的影响

4.3 桩井布置形式影响

图10为不同桩井布置形式的固结度对比.从图10可以看出，模型A中桩井布置方式采用np=1/2(三角形密集型)，大幅度加快了地基土的固结，且远比np=1(矩形布置)固结快.模型B随着nd增大，固结速率提高，地基土固结时间大幅缩短.nd的变化实际上是塑料排水板增加后的反应，搅拌桩周围的排水通道增加，极大地加快了地基土固结.高速公路施工过程中，在沉降速率要求的范围内，可采用增设塑料排水板来加速地基土固结，减少不均匀差异沉降.

图10 不同桩井布置形式的固结度对比

5 结 论

本文针对塑料排水板联合水泥土搅拌桩复合地基的固结理论，通过分析得出如下结论：

1) 本文推导的模型A和模型B固结控制方程与卢萌盟的控制方程相比，其解在形式上是一致的，具体差别在于参数的取值不同.

2) 模型A和模型B复合地基的固结速率随着搅拌桩与竖井直径比的增大而大幅度增大，模型B固结总是快于模型A，与卢萌盟解相比，本文固结度总是慢于卢萌盟解，井径比较大时，本文解更精确.

3) 竖井扰动区渗透系数比搅拌桩扰动区的渗透系数对固结速率的影响大，此时本文固结度与卢萌盟解的最大差值约为4%.

4) 桩井布置形式对模型A和模型B的固结速率影响主要体现在塑料排水板的布置密度上，模型A的三角形布置形式固结速率是最快的，因此，增加塑料排水板可提高地基土的排水能力.