6016-T4铝合金高应变速率变形行为和本构模型

郑文涛， 于佳卉， 王志惠， 陈晶华， 苏 明

(1. 沈阳工业大学 材料科学与工程学院， 沈阳 110870； 2. 国网青海省电力公司 电力科学研究院， 西宁 810001)

目前，6000系列铝合金是实现汽车轻量化的主要铝合金之一，因其具有成形性能好、耐腐蚀、着色能力强等特点，主要应用于汽车车身的生产[1-2].Bobbili等[3]发现7017铝合金在应变速率为1 500～4 500 s-1范围内的流变应力随着应变速率的增加而变大.Liu等[4]发现7055铝合金在应变速率为1 000～4 000 s-1时表现出正应变速率敏感性，在应变速率为4 000～6 000 s-1时表现出负应变速率敏感性.朱必武等[5]研究发现，Al-Mg-Si-Cu铝合金的应变速率敏感性较小，当应变速率在800～5 200 s-1范围内时，流变应力未随应变速率的增加而增加.张子群等[6]发现，当室温下2219铝合金的应变速率为1 000～3 000 s-1时，合金产生的变形热能够引起试件温度上升，由此带来的热软化效应与应变速率强化作用相抵消，合金表现出的应变率敏感性很弱.毛萍莉等[7]研究了动态压缩中AZ31B镁合金和6065铝合金的变形过程，建立了Johnson-Cook本构方程，并运用ANSYS/LS-DYNA软件进行了仿真模拟.乔曦等[8]针对5357铝合金的变形实验建立了三种本构模型，利用仿真软件分析后发现Johnson-Cook和Cowper-Symonds本构模型能够更加准确地描述5357铝合金的力学性能变化.赵士忠等[9]针对6008铝合金建立高应变速率本构模型时，考虑了绝热温升对合金力学行为变化的影响，利用Cowper-Symonds模型修正Johnson-Cook模型，所得拟合应力应变曲线与实验数据更加吻合.在实际应用中，当铝合金作为车用板材生产和使用时，必定会受到高速冲击载荷的作用，因而研究6016-T4铝合金轧制板材在高应变速率条件下的力学行为变化是十分有意义的.本文通过研究6016-T4铝合金的力学性能变化，建立相应本构模型来描述其变形行为，同时运用ABAQUS软件进行仿真模拟，对比不同应变速率条件下合金的变形特点，以期为合金的应用提供相关参考.

1 材料及方法

实验材料为6016-T4铝合金轧制板材，其化学成分如表1所示.在板材上取轴线方向与轧制方向平行的圆柱形试件，其规格为φ6 mm×6 mm.实验分为两部分：第一部分是采用分离式霍普金森压杆(SHPB)设备进行应变速率为1 600、2 300和3 200 s-1的高应变速率压缩变形实验；第二部分是采用万能实验机进行应变速率为0.001 s-1的准静态压缩实验.

表1 6016-T4铝合金的化学成分(w)

图1为SHPB设备示意图.SHPB设备主要由子弹发射系统、入射杆、透射杆、信号采集系统等设备构成，杆类材料为55CrSi弹簧钢，直径为14.5 mm，入射杆和透射杆长度均为1 000 mm，子弹长度为300 mm.实验时子弹在高压气体作用下撞击进入射杆，通过改变气压大小来调节子弹的撞击速度，从而改变实验时的应变速率[10].

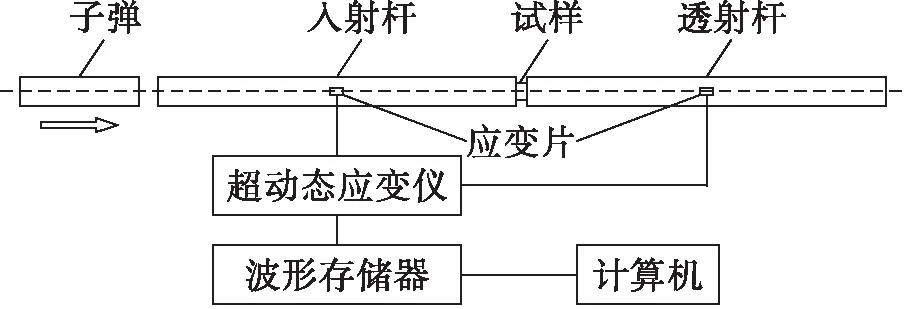
图1 分离式霍普金森压杆设备示意图

采用维氏硬度计对压缩前后的试件进行硬度测试，为保证测试结果的准确性，测量每个试件硬度时记录三组有效数据，求出平均值作为硬度测试结果.

2 结果及分析

2.1 力学性能

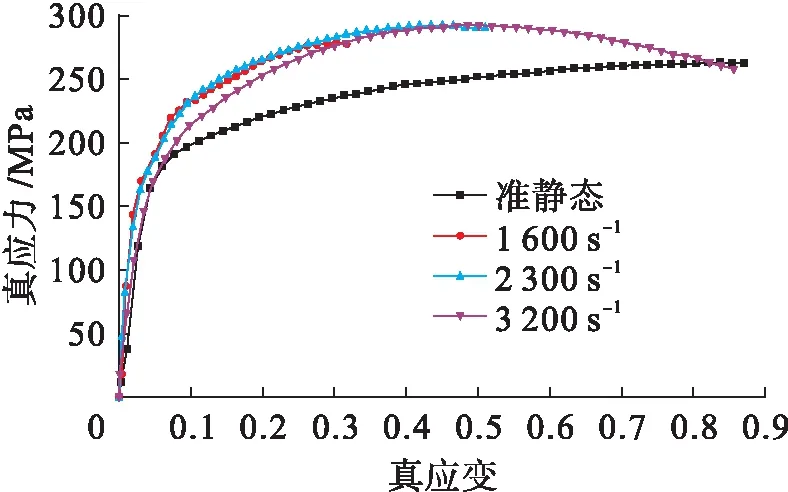
图2 合金在不同应变速率下的真实应力应变曲线

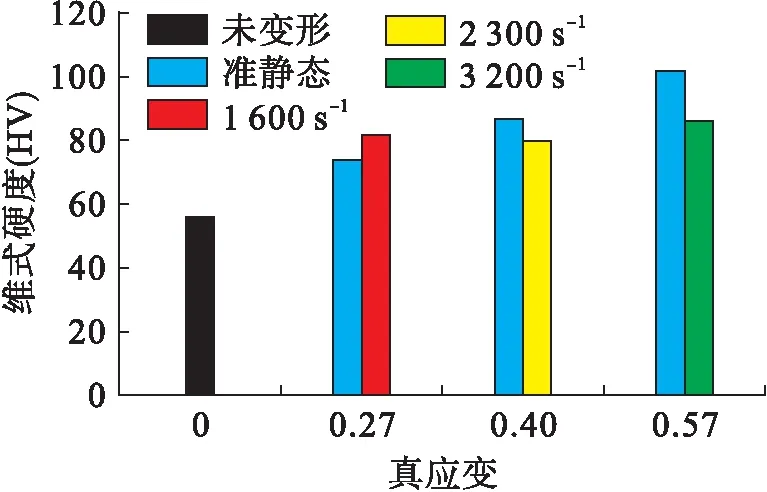
图3 合金板材压缩变形前后的硬度

2.2 本构模型及参数

针对6016-T4铝合金板材在不同条件下的高应变速率变形行为，需要建立本构模型来反应其力学性能变化，本文选用Johnson-Cook本构模型(简称J-C本构模型)，其本构关系式[11]为

(1)

室温高应变速率压缩实验近似为绝热温升过程，变形过程中材料温度变化值的计算表达式[13]为

(2)

式中：η为总塑性功转化为热量的比例系数，一般铝合金高应变速率压缩变形实验中取0.9[14]；cv为定容比热容，常温下铝合金取值886 J/(kg·K)[15]；ρ为实验材料密度，铝合金密度为2.7×103kg/m3；ε为真实塑性应变；σ为真实流变应力.利用式(2)求出三种变形条件下6016-T4铝合金板材的绝热温升分别为31.9、66.2和101.1 ℃.

当计算参数A、B和n时，可将J-C本构模型简化为

(3)

当计算参数C时，需要忽略温度对流变应力的影响，即将J-C本构模型简化为

(4)

当计算参数m时，将J-C本构方程转化为

(5)

本文中Tr取20 ℃，TM取650 ℃，将已知参数和不同变形条件下的应变、对应的真实应力与绝热温升代入T*的计算表达式和式(5)中，得到相应的常数m，对其求平均值后可得m=1.256 8.6016-T4铝合金板材J-C本构模型参数如表2所示.

表2 合金板材J-C本构模型参数

图4为6016-T4铝合金板材在不同应变速率下本构模型计算数据与实测数据的对比结果，由图4可见，两种数据偏差较大，说明建立的J-C本构模型不能准确地表达出该合金在变形过程中的力学行为变化.

图4 合金板材的实测值与J-C本构模型计算值的比较

C=c0+c1T*+c2T*2

(6)

表3 修正后J-C本构模型参数

6016-T4铝合金板材J-C本构模型的最终表达式为

(1-T*1.303 1)

(7)

C=0.005 3+0.433 1T*-3.645 7T*2

(8)

表4 修正后J-C本构模型参数C值表达式系数

修正J-C本构模型后，6016-T4铝合金板材在不同应变速率下的计算数据与实测数据对比结果如图5所示.由图5可见，两种数据偏差很小且吻合良好，说明修正后的J-C本构模型可以较为准确地表达出该合金的力学行为变化.

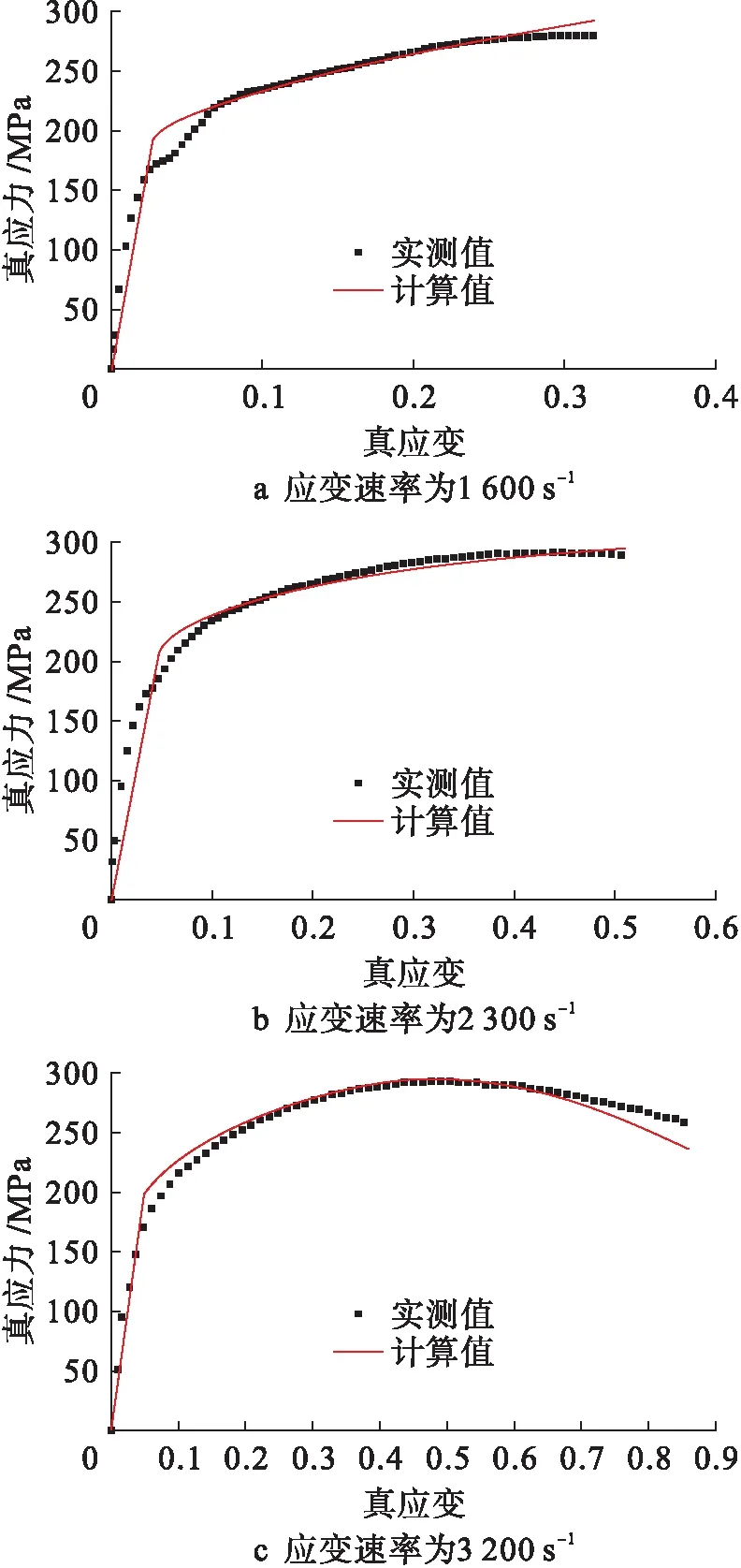
图5 合金板材的实测值与修正后J-C本构模型计算值的比较

引入平均相对误差AARE和均方根误差RMSE这两个统计参数指标，对修正前后的模型拟合准确度进行评估，其表达式[16]分别为

(9)

(10)

式中：Ei为实测值；Pi为计算值；N为样本个数.

平均相对误差和均方根误差可以反映相关数值之间的紧密程度.实测值与修正前后J-C本构模型计算值的AARE和RMSE计算结果如表5所示.由表5可见，修正后J-C本构模型的AARE和RMSE均小于未修正的情况，即修正后的J-C本构模型计算值更加接近实测值.

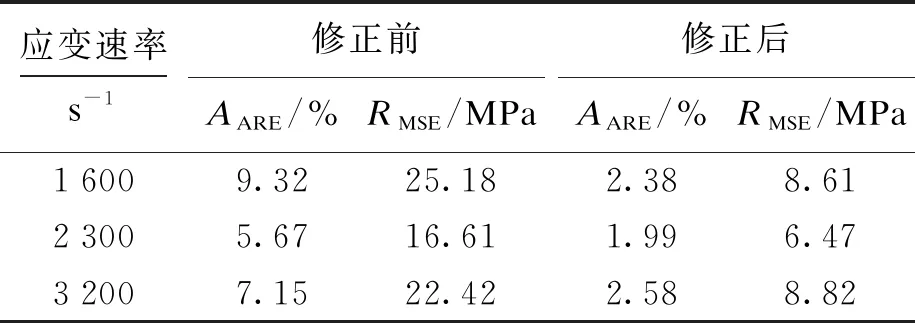
表5 修正前后J-C本构模型的指标计算结果

2.3 SHPB实验仿真模拟

高应变速率变形是一个瞬间发生的过程，持续时间极短，本文应用ABAQUS软件根据建立的J-C本构模型对变形过程进行模拟，分析试件的温度变化情况.

SHPB设备结构入射杆和透射杆的模型尺寸均为φ14.5×1000 mm，试件的模型尺寸为φ6×6 mm，为了节省运算时间，针对全模型的四分之一部分来进行模拟.采用六面体(Hex)单元3维8节点缩减积分单元(C3D8R)和3维8节点热效应耦合缩减积分单元(C3D8T)分别对压杆模型和试件模型划分出均匀的网格，结果如图6所示.

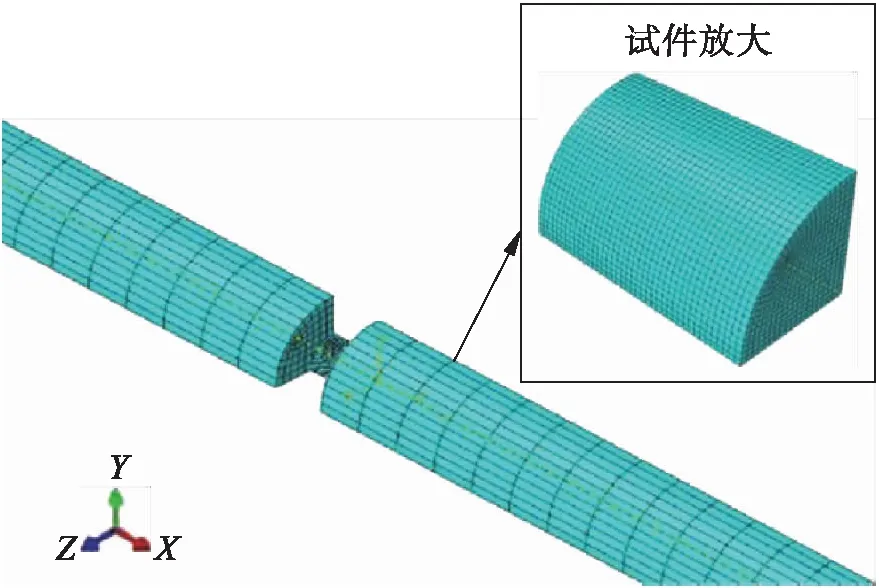
图6 三维有限元模型

压杆材料为55CrSi弹簧钢(采用线弹性模型进行分析)，密度为7.85×103kg/m3，弹性模量取210 GPa，泊松比取0.3[12].铝合金试件弹性模量取68 GPa，泊松比取0.3，比热容为886 J/(kg·℃)，热传导系数和非弹性热分数分别为158 W/(m·K)和0.9[15-17].当设置材料塑性参数时，硬化阶段选取软件自带的J-C本构模型选项，并添加本构模型的各个参数进行分析.由于在室温下进行实验，因此，压杆和试件的初始温度都设置为20 ℃.假设压缩产生的热量不在试件与压杆、试件与空气中发生热传导，由此模拟试件的绝热温升.

试件变形后的温度场模拟结果如图7所示.由图7可知，温度场的分布是不均匀的，试件与压杆接触的圆形边缘处温度始终是最高的，试件的外表面温度较低且低于试件中心温度，但试件表面与中心之间部分的温度较高.

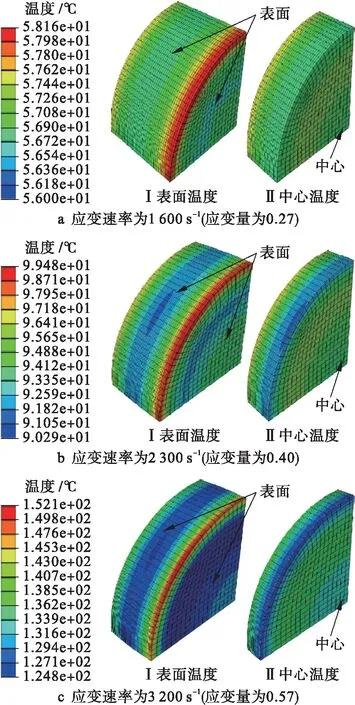
图7 不同条件下变形后试件的温度场分布

在不同条件下变形后试件的温度场统计结果如表6所示.由表6可见，模拟平均温度与理论计算温度之间误差不超过10%，在可以接受的范围之内.可见，采用建立的J-C本构模型进行高应变速率压缩过程模拟，可以得到较为准确的试件温度场分布.

表6 不同条件下变形后试件的温度场统计结果

3 结 论

1) 在高应变速率压缩变形过程中，当应变速率为1 600～3 200 s-1时，6016-T4铝合金板材在应变速率较高时呈现出负应变速率敏感效应.

2) 根据应变速率的不同，可以建立6016-T4铝合金轧制板材的J-C本构模型，在本文应变速率范围内，由本构模型计算出的数据与实验数据基本吻合.

3) 应用ABAQUS进行有限元仿真模拟后发现，试件变形后的温度场分布不均匀，模拟温度与理论计算温度误差在10%以内，模拟结果比较准确.