基于神经网络模型的智能电网线损估计方法*

李 果， 袁小凯， 黄世平

(中国南方电网有限公司 科学研究院， 广州 510080)

配电网中电能在传输过程中会在线路上产生功率损耗，这种配电网线路的功率损耗会危及配电网的安全、可靠运行.目前配电网线路的降损技术一般采用配电网优化重构[1-2]或采用电容器进行无功补偿[3-4].

配电网线损通常可以划分为技术损失和非技术损失.技术损失是指配电网中电能在传输、转换和分配过程中由于输变电设备的工作特性导致的损耗；非技术性损失是由于人为过失或盗电而产生的.通常情况下，因为技术损失与输变电设备的材料特性和其阻抗有关，所以技术损失远大于非技术损失.张世翔等[5]对技术损失与其对配电网安全性的影响进行了研究.Fragkioudaki等[6]详细介绍了非技术损失的检测方法.计算线损的经典方法是在假设导体尺寸恒定、沿着馈线的负载分布均匀的条件下，通过设定总负载集中在距馈线开始的1/3距离处，对线路损耗进行计算.该方法的缺点是不能在导体尺寸不规则和负载分布不均匀的条件下工作，因此虽然该方法的计算速度较快，但与实际值偏差较大.Hong等[7]在经典算法的基础上进行改进，提出了经验法，实现了导体尺寸不规则条件下的线损计算.然而，尽管此方法比传统方法更实用，但在计算速度与准确度上仍具有较大的局限性.魏超峰等[8]详细介绍了电阻损耗、变压器铁心损耗及非技术损耗的机理，证明了计算未标定负载损耗的方法取决于损耗类型.Nadira等[9]提出了一种使用有限的数据集来计算线损的方法，该方法能够准确分析线路的非技术损失.

以往方法的问题在于需要较长时间来实时计算功率损耗，同时计算条件要求较高，难以适应实际的工程应用.本文提出了一种快速、准确的神经网络模型，主要使用改进的BP神经网络对线路损耗进行实时计算.该模型通过使用输入数据的负载曲线训练模型，可以较为准确地计算配电网线路损耗.

1 BP神经网络优化算法

1.1 BP神经网络算法

BP神经网络的前向传播过程是从输入层输入数据，经过隐藏层传递到输出层的过程[10-12].若通过正向的运算结果不满足期望的收敛值，则输出将通过反向误差传递，修正神经网络的权值和阈值，从而实现神经网络的自学习，直至前向输出达到预期效果.

设BP神经网络有n个输入节点，l个输出节点，m个隐藏层节点，设定输入向量为X=(x1，x2，…，xn)T，隐藏层的输出向量为H=(h1，h2，…，hj)T，输出层的输出向量为O=(o1，o2，…，ok)T，输入层与隐藏层之间的权重为ωij，隐藏层与输出层之间的权重为ω′ij，隐藏层的阈值向量为α=(α1，α2，…，αl)T，输出层的阈值向量为β=(β1，β2，…，βm)T，相应的期望向量设定为E=(e1，e2，…，ek)T.

BP算法的正向传播可表示为

(1)

(2)

输出误差可表示为

(3)

将式(2)代入式(3)可得

(4)

1.2 LM优化算法

F[ω(n+1)]=F[ω(n)]+gT(n)Δω(n)+

0.5ΔωT(n)A(n)Δω(n)

(5)

式中：gT(n)为梯度向量的转置；A(n)为Hessian矩阵.当满足条件Δω(n)=-A-1(n)g(n)，可得到误差函数F的最小值.

为了避免直接计算Hessian矩阵，LM算法将Hessian矩阵近似为

A=JTJ

(6)

式中，J为雅可比矩阵，则梯度向量为

g=JTF

(7)

权重和阈值的校正方法可表示为

ω(k+1)=ω(k)-[JTJ+μI]-1JTF

(8)

α(k+1)=α(k)-[JTJ+μI]-1JTF

(9)

式中，μ为惩罚因子.当其大于0时，协方差矩阵(JTJ+μI)恒为正数，从而保证权重和阈值的梯度下降方向正确.

BP神经网络算法可以通过反向传播迭代计算来连续更新隐藏层与输出层的权重和阈值.更新后的参数不仅可以继承上一代参数的信息，且还优于上一代参数.经过LM算法优化迭代计算后，基于BP网络的计算精度将持续提高，最终可以适应智能电网中配电网线损估计的精度要求.

2 线损估计方法

2.1 神经网络模型

通过样本数据训练优化后的BP神经网络，可以获得线损估计的神经网络模型.在实际应用过程中，将计算模型估计线损值与实际测得的线损值进行比较，并采用优化算法对权重和阈值进行连续优化，以提高估计模型的精度，从而满足智能电网运行可靠性的要求.

在利用优化后的BP神经网络构建神经网络模型，进而估计配电网线损时，关键问题在于输入与输出之间非线性函数关系的拟合.采用潮流法生成数据与配电网负载曲线，神经网络的输入数据由负载系数乘以系统的负载表示.负载系数是一组有限的时序样本，可以表示为

L=[LM1，LM2，…，LMq]

(10)

式中：M为持续时间的时间步长；q为指定持续时间的样本数.网络的输出表示为沿设定连续时间在每条线路上的功率损耗，则输出矩阵可表示为

(11)

式中：r为行数；t为数据集的负载系数样本；c为需要估计的线路数；d为负载样本的数量.

2.2 神经网络模型估计线损流程

基于神经网络模型的线损估计方法主要利用两个综合数据集(随机数据集和单日数据集)对线损进行估计.利用潮流法对生成的数据进行采样和求解，然后使用相应的数据集训练神经网络进行学习.当输入数据产生任何变化时，该模型均可直接、准确地再现相应的输出结果，无需进行潮流计算.神经网络模型线损估计流程如下：

1) 通过潮流法生成由负载样本构成的输入数据集并求解；

2) 使用反向传播迭代计算确定梯度，创建BP神经网络模型；

3) 使用输入数据集作为神经网络模型训练集来训练模型.

4) 采用LM算法优化BP神经网络模型，迭代求解误差函数，不断更新网络权重和阈值，直到达到停止误差函数最小值标准(最大迭代次数为10 000次，最小梯度误差为5%，模型输出误差不超过0.001)；

5) 输出线路损耗估计结果.

2.3 有效性评估指标

为了验证所提方法的准确性，需要计算神经网络模型输出与目标输出之间的误差.本文采用均方误差(MSE)表征神经网络模型输出与第i条线路的实际功率损耗之间的误差，该均方误差表示在连续时间T内从第c条总线到第c+1条总线的功率损耗，计算表达式为

(12)

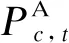
均方根误差(RMSE)和相对误差(RE)[13-14]的计算表达式为

(13)

(14)

3 实验验证

3.1 实验条件

本节使用提出的神经网络模型方法对智能电网中配电网线路的功率损耗进行实时估计.实验所用的计算机处理器为Intel(R) Core(TM) i5-7400 CPU，工作频率为3.00 GHz，安装内存为8.00 GB，模型通过MATLAB 2014a实现.如图1所示，实验在具有32条线路的IEEE33节点系统上进行，实验参数如表1所示.根据大量专家学者采用神经网络进行线损计算的经验[15-17]，本文训练样本集的神经网络采用12×6×3的结构，即输入层神经元为12个，隐藏层神经元为6个，输出层神经元为3个，其中输入层和隐藏层的传递函数是tansig，输出层的传递函数是logsig，模型中权重和阈值通过调用newff函数，经归一化处理后随机生成取值范围为0～1的随机数.应用LM优化算法时采用trainlm函数训练模型，以误差函数F的最小值为目标函数，利用LM法不断修正模型中各层权重和阈值，设定最大迭代次数为10 000次，目标最小梯度误差设定为0.05，模型初始学习速度设定为0.02，将样本集数据导入模型中进行训练.

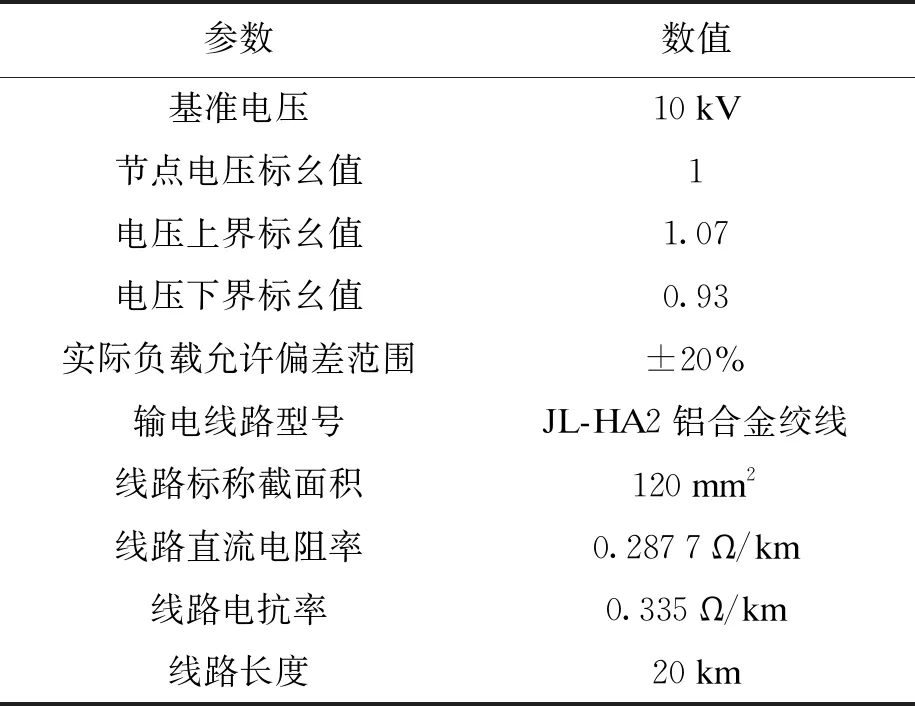
表1 实验参数

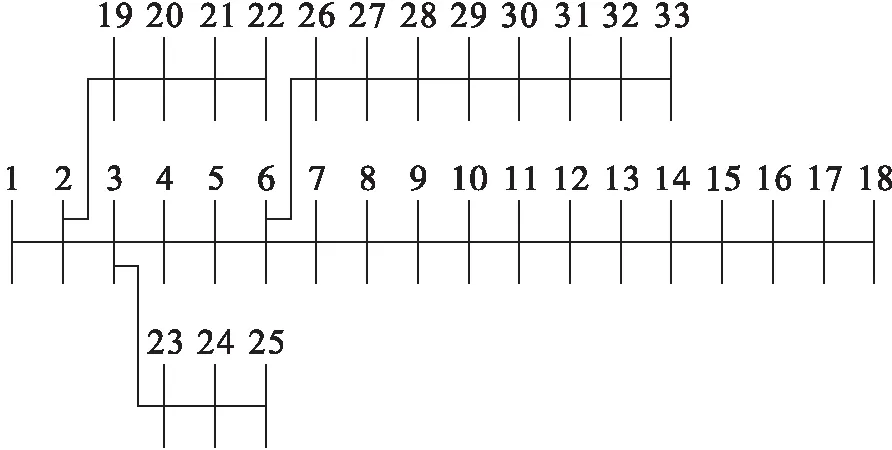
图1 IEEE33节点系统

3.2 实验结果

训练集样本为4个IEEE33节点系统，共128条线路的功率损耗数据.由于IEEE33节点系统中1号线路、10号线路和30号线路在采用潮流法估计线损时偏离实际数值较大，相较其他线路具有特殊性，因此以训练集中1号线路、10号线路和30号线路为例，将3条线路实际功率损耗与神经网络模型估计功率损耗进行比较，比较结果如图2～4所示.由图2～4可以看出，使用神经网络模型在指定线路处估计的线路功率损耗接近实际的功率损耗.

图2 1号线路线损估计结果比较

图3 10号线路线损估计结果比较

图5给出了训练集中所有线路的实际总功率损耗与神经网络模型估计的总功率损耗对比结果.可以看出，总体上神经网络模型估计的线损与实际线损相近.同时，将收集到的智能电网中配电网1 440条线路线损数据作为测试集，将其导入神经网络模型中估计线损，测试集线损对比结果如图6所示.从图6中可以看出，神经网络模型对于测试集估计的线损与实际线损同样相近.

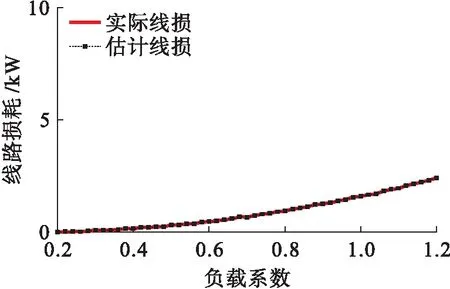
图4 30号线路线损估计结果比较

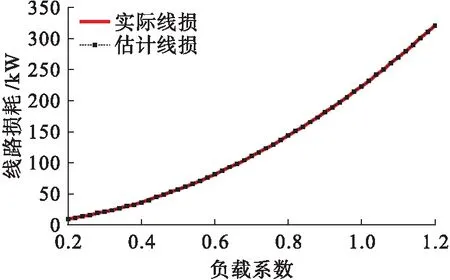
图5 训练集线路总损耗估计结果比较

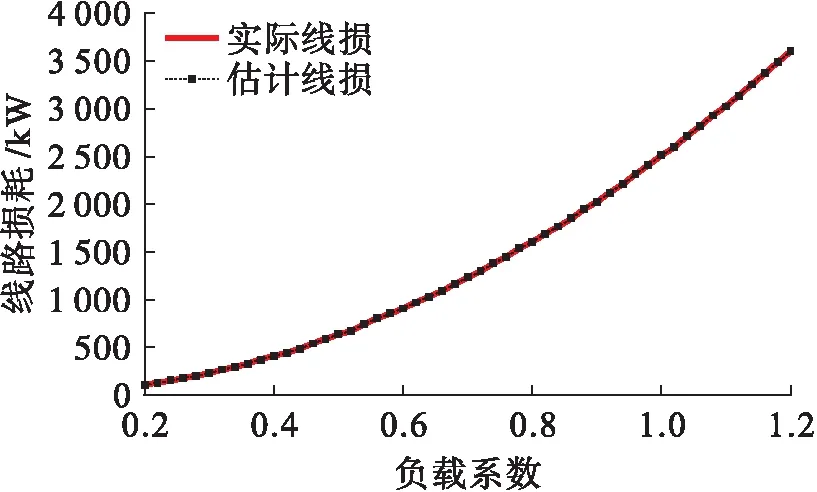
图6 测试集线路总损耗估计结果比较

基于表1中实验参数分别采用神经网络模型和潮流法计算线路线损，可通过计算MSE、RMSE和RE来评估神经网络模型的精度.表2给出了神经网络模型和潮流法在估计训练集和测试集中各条线路功率损耗时MSE、RMSE和RE的平均值MMSE、MRMSE与MRE.由表2可以看出，神经网络模型估计线路损耗时的各项评估指标评价均较为优秀，相比于潮流法具有更高的精度，表明该方法估计精度较高.此外，当数据集样本增大时，应用神经网络模型估计线损的均方误差、均方根误差和相对误差明显减小，而潮流法误差明显增大.这表明神经网络模型对于样本容量具有较好的适应性，因此，在将模型应用于工程实际中时可以酌情考虑增加估计样本数量.

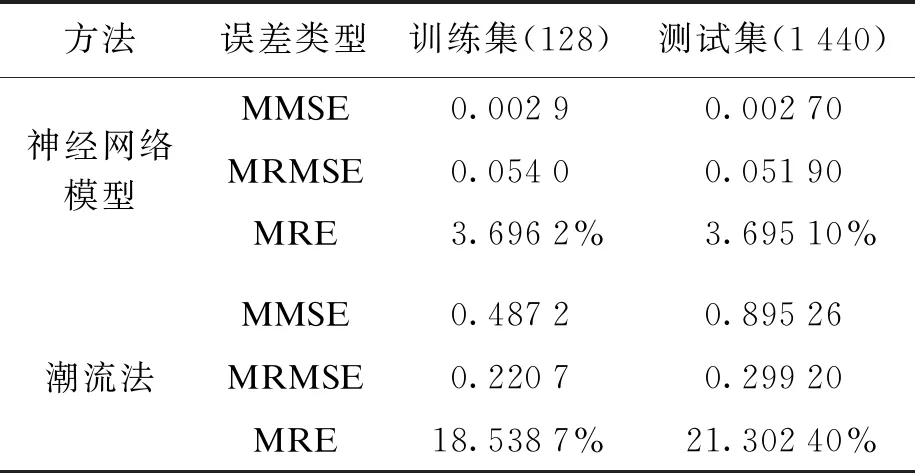
表2 方法有效性评估指标

两种算法平均运算用时结果如表3所示，神经网络模型程序的平均运算时间明显小于传统的潮流法程序的平均运算时间.神经网络模型在用于训练集和测试集时的迭代次数分别为566次和1 489次，且随着数据集样本容量的增加，前者的运算时间增幅极小，而后者则需要较多的运算时间.这表明传统的潮流法难以应对大样本的数据集，而神经网络模型则可以较好地应用于此类数据集中，其工程应用的可靠性更佳.

表3 不同方法的平均运算用时

4 结 论

本文提出了一种基于神经网络模型的智能电网线损估计方法，其能够快速、准确地对智能电网中配电网的线路损耗进行实时分析并估计功率损耗.相比于传统的潮流法，该方法具有训练快、精度高和适应性强等特点.将该方法应用于实际配电网线损数据集分析中，其估计误差较小，同时运算速度较快.当数据集样本容量显著增加时，神经网络模型的运算准确度和运算速度不受影响，因此，智能电网中配电网的线路损耗均可以使用神经网络模型方法在较短的时间估算得到，而无需像潮流法一样计算系统所有线路的损耗.本文所提出的基于神经网络模型的智能电网线损估计方法，可以较好地应用于智能电网运行状态的实时分析，有助于降损技术的研究和维护电力系统的安全、稳定运行.但是由于BP神经网络模型中隐藏层节点数目主要依据历史经验进行设定，导致模型收敛速度稍慢，容易出现局部极小的情况，因此下一步计划采用智能算法对模型进行改进，提升模型收敛速度，弥补模型不足，提高模型估计线损的效率.