AMESim仿真软件在电液伺服系统教学中的应用
曾亿山,张 涛,虢 锐,高文智
(合肥工业大学 机械工程学院,安徽 合肥 230009)
“液压伺服系统”课程中涉及到了众多元件和系统的传递函数,这些函数形式复杂,简化过程十分复杂,学生理解难度较大,难以留下深刻印象。以力反馈两级电液伺服阀为例,其传递函数涉及到许多复杂的电压方程、运动学方程、动力学方程,对其进行稳定性分析、传递函数简化、估计频宽时,若单是进行理论推导,不仅理解难度大,还会大大降低学生的学习积极性。因此,在理论推导的基础之上,引入AMESim软件进行仿真,在判断系统稳定性时,通过软件画出其力反馈回路伯德图,能使学生更直观地理解其稳定条件。而在传递函数简化时,通过软件设置不同的固有频率,能更清楚地展现其传递函数简化的结果。
1 软件简介
AMESim软件能为多个领域提供由简单到复杂的仿真平台[1]。用户可在此平台上建立复杂的、多学科领域的系统模型,并在此基础上进行方正计算和深入分析,同时,也可以在此平台上研究任何元件或系统的稳态或动态性能。其模型是基于系统的物理模型建立的,这可以使一般用户不必经历复杂的数学建模过程,而是通过物理机理直接搭建模型,使仿真操作变得简单。在子模型模式下给每个元件设置不同的子模型以建立相应的数学模型,根据实际要求定义工作参数,然后进行仿真,完成对系统或元件的模拟[2]。
AMESim用户界面如图1,主要包括主窗口、主菜单、工具栏、和右侧的元件库。在草图模式下,通过拖拽右侧元件库中的图标,用户可以自由搭建自己所需要的模型,此外,通过“帮助—实例帮助”可直接使用软件中建立好的模型。在子模型模式下选择不同子模型,软件将为元件分配相应的数学模型。在参数模式下可以对每个元件的细节参数进行设置。在运行模式中可以运行仿真并对仿真结果进行处理。
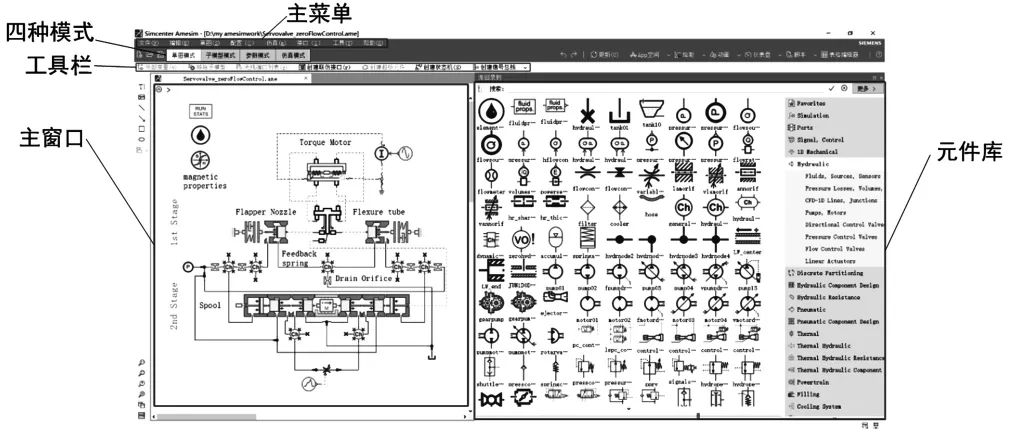
图1 AMESim用户界面
2 AMESim力反馈两级电液伺服阀仿真建模
虽然在诸如“液压伺服系统”、“液压与气压传动”等许多工程设计中都可以用到AMESim软件,但目前课程教学中该软件的应用较少[3],若将其加入到这些课程的教学之中,既能更为方便的验证结论的正确性,使学生们对课程结论留下更加深刻的印象,同时也可以给原本枯燥的理论推导带来一些趣味性,提高学生们的积极性,促进学生们的学习。
2.1 力反馈两级电液伺服阀简介
力反馈两级电液伺服阀由于挡板和衔铁均在中位附近工作,线性好。对力矩马达的线性要求也不高,可允许滑阀有较大的工作行程。常见的力反馈两级电液伺服阀结构原理图如图2所示。图中N和S分别为永磁铁的北极和南极,Ps为供油压力,PL和PL分别为负载负载的压降和流量。其第一级液压放大器为双喷嘴挡板阀,通过永磁动铁式力矩马达控制,第二级放大器为四通滑阀,阀芯的位移与衔铁挡板组件通过反馈杆相连,共同构成滑阀位移力反馈回路。
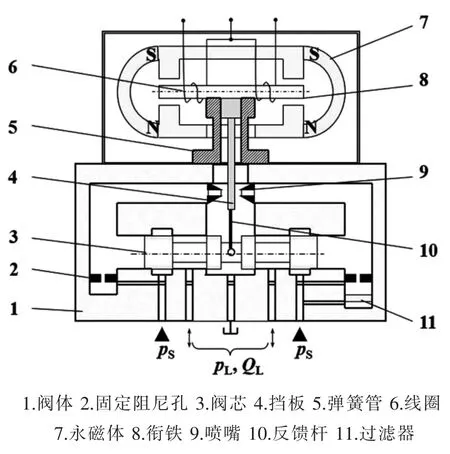
图2 结构原理图
滑阀位移力反馈回路的工作原理:没有电流输入时,由于反馈杆的约束,阀芯处在中位,有控制电流通过时,产生的电磁力矩使衔铁板组件逆时针转动,使反馈杆变形[4]。喷嘴挡板阀两端间隙产生变化,滑阀两腔产生压差,阀芯左移。阀芯左移使反馈杆形变产生的力矩与电磁力矩趋于平衡。阀芯左移过程中,挡板阀左右间隙趋同,滑阀阀芯两端压差减小,各力平衡时,阀芯停止运动。阀芯的位移与控制电流成比例,在负载压差一定时,阀输出的流量与控制电流也成比例。其传递函数方块图如图3所示。

图3 传递函数方块图
由图3可见,力反馈两级电液伺服阀的方块图主要包含两个反馈回路,主要回路是滑阀位移的力反馈回路,次要回路是作用在挡板上的压力反馈回路。可见力反馈两级电液伺服阀的传递函数相当复杂,若是只进行理论推导的话,将给学生带来较大的理解难度和记忆难度。引入AMESim仿真辅助教学可以较好地解决这个问题。
2.2 力反馈电液伺服阀AMESim仿真
在AMESim软件中打开力反馈两级电液伺服阀的实例,其模型如下图4,模型中包含有力矩马达部分,先导阀部分,主阀部分,以及反馈杆、弹簧管等元件,此模型很好地还原了力反馈两级电液伺服阀的数学特征[5]。同时此模型可在AMESim软件(帮助—实例帮助)中直接获取,操作方便,可在课堂中直接应用。
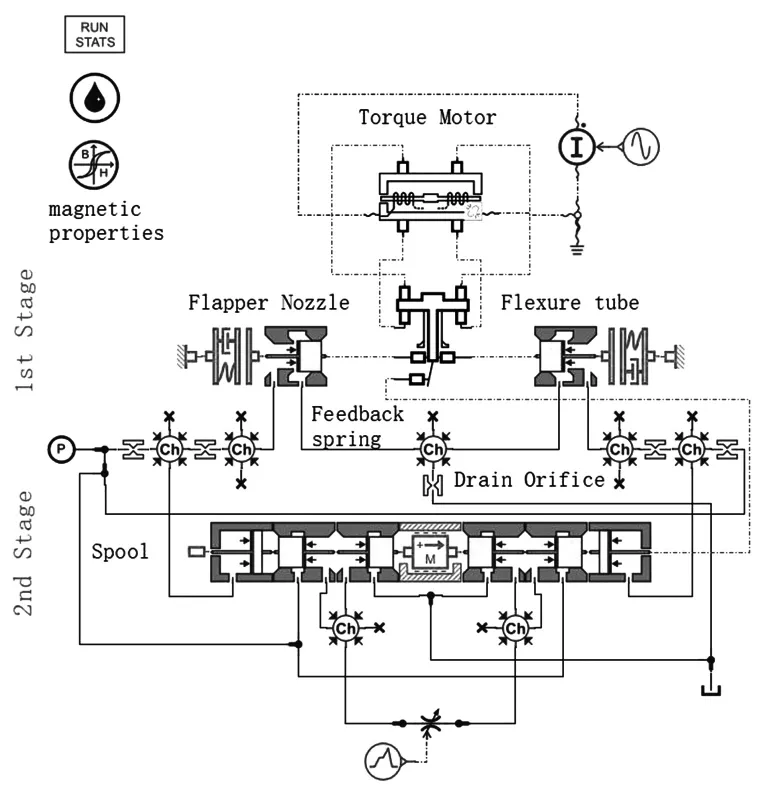
图4 AEMSim力反馈两级电液伺服阀模型
3 AMESim在力反馈电液伺服阀教学中的应用
在建立好力反馈电液伺服阀的AMESim仿真模型后,将其应用到力反馈回路稳定性分析和电液伺服阀传递函数简化的教学中,在运行模式下进行仿真并利用AMESim软件强大的后处理能力绘制相应的曲线或图表,更为生动地展示课本中的结论,降低学生的理解难度。
3.1 在力反馈回路稳定性分析教学中的应用
力反馈伺服阀的稳定性分析包括压力反馈回路的稳定性分析和力反馈回路的稳定性分析两部分,其中压力反馈回路的稳定条件一般情况下很容易得到满足[6],不是本次分析的主要对象。而力反馈回路的稳定性条件为Kvf<2ξmfωmf[7],在教学中,通过分析衔铁转角与挡板位移之间的关系、滑阀的动态特性、马达的运动方程以及作用在挡板上的力反馈等一系列物理过程并将之简化才能得到上述结论。此过程较为繁杂,并且完成纯理论推理后学生也较难记住结论,若在推理过程成加入AMESim仿真来验证或者辅助推理,将会使原本繁杂的过程别的清晰,同时也利于提高学生的积极性。
比如在滑阀动态特性简化时,由于滑阀的固有频率远大于衔铁挡板组件的固有频率,可忽略滑阀的动态,将其视为比例积分环节。但这样的纯理论推导难以给学生们留下印象,在课堂上引入AMESim软件既可以验证简化假设的正确性,同时也能让学生们对此结论留下更深刻的印象。运用前文所述的仿真实例,将喷嘴挡板的位移状态设置为control(即控制状态),将主阀的位移状态设置为state observer(即观测状态),运行仿真,可得到喷嘴挡板到阀芯位移的幅频特性图,如下图5所示,观察曲线,不难看出其具有积分环节的特征。
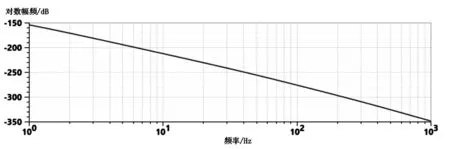
图5 挡板到阀芯位移幅频特性图
与之相同的,在验证力反馈回路稳定性条件时,运行仿真,设置力矩马达的输出转矩为力反馈回路的输入,滑阀位移为输出,直接按照AEMESim实例中的参数来运行仿真,得到力反馈回路的开环伯德图,可见存在一谐振峰值,尝试改变力反馈回路的开环放大系数,当谐振峰值超过零分贝线时,系统不再稳定,可验证此时Kvf≥2ξmfωmf。在简化其他环节时也可以按此操作,以方便学生们理解和分析。
3.2 电液伺服阀传递函数简化教学中的应用
在对伺服阀整体传递函数简化的时,可以将伺服阀用一个二阶振荡环节来表示。与前述稳定性分析时相同,如果仅用纯理论推导,有较大的理解难度和记忆难度。引入AMESim仿真来验证结论以加深印象。
将输入电流状态设置为control(即控制状态),阀出口流量状态设置为observer(即观测状态),不改变实例参数,运行仿真,得到空载流量关于伺服阀输入电流信号的伯德图,如下图6。观察伯德图的曲线,很明显看出,此伯德图具有二阶振荡环节的特征[8]。

图6 输入电流到空载流量的伯德图
在后续传递函数简化时,只需改变伺服阀二阶环节的固有频率,按照相同的操作,可得到不同情况下伺服阀传递函数的简化结果。
4 结语
以力反馈电液伺服阀这一教学环节为例,在力反馈回路稳定性分析和电液伺服阀传递函数简化的教学过程利用AMESim软件来分析系统验证结论。可以看到,在课程中引入AMESim软件辅助教学,能够使学生们对原本复杂的数学模型有一个更为直观的认识,使繁杂枯燥的纯理论分析更加生动,平衡其难度,降低学生们的理解难度。后续可将软件引入到诸如控制工程基础、液压与气压传动等更多相关课程的教学当中。

