纵连板式无砟轨道热致隆起屈曲解析解

高咪，杨国涛

（青岛理工大学土木工程学院，山东青岛 266525）

0 引言

温度荷载作用下，纵连板式无砟轨道线路中会产生较大轴力而导致上拱失稳，使得轨道板与其下方的CA 砂浆层分离，出现离缝现象[1，2]。当前多数研究仅以轨道板为研究对象，忽略了钢轨对结构上拱的影响[3，4]。杨俊斌等[5]假设以正弦型作为CRTSⅡ型轨道板的变形曲线形式，推导其竖向稳定性的临界力计算公式；朱永见[6]根据微分方程法得出轨道板在纵向约束力作用下的解析解；赵林等[7]利用功的互等法推导了高温荷载作用下弹性薄板的功的互等定理；钟阳龙等[8]通过建立三维有限元分析模型，验证了基于内聚力模型来模拟轨道板和砂浆层间复杂的作用关系具有可靠性；张向民等[9]利用能量变分原理和瑞利-里兹法分析了轨道板与砂浆层在不同阶段的临界温度力，并表明了钢轨对无砟轨道的稳定性影响有显著影响，在分析中不可忽略。

文中对钢轨和轨道板组成的组合结构上拱屈曲行为进行系统研究，利用能量变分法求解存在窄接缝损伤时，纵连板式轨道完善状态下上拱屈曲安全温度的闭合解，明确上拱过程中的受力和变形特点，可为相关设计优化提供理论依据。

1 基本假定

（1）将轨道结构沿纵向简化为无限长二维梁模型，材料服从胡克定律，且符合平截面假定。

（2）扣件刚度对结构失稳影响较小，在计算中可不予考虑。

（3）屈曲抬升区域的重量ql1支承在脱空点处，会在这个位置产生一个集中的阻力，如图1 所示。

图1 轨道结构示意图

1.1 等效换算

轨道上拱实质由钢轨和轨道板两部分组成见图2，且二者线膨胀系数相差不大，故在满足小变形假设的前提下，采用换算截面法[10]，将钢轨面积换算为轨道板混凝土面积，并保持换算前后单元面积承受的合力大小不变、应变相等，可得到整体结构的等效抗弯刚度和等效抗压刚度。

图2 轨道结构横截面示意图

式中，σ、ε、A 表示材料的应力、应变和面积；下标c、s 分别代值轨道板的钢轨；且nE为钢材与混凝土的弹性模量之比，nE＝Es/ Ec，换算截面中心轴位于混凝土板内，设中心轴至混凝土底部的距离为，yOU对底部静矩相等，则有：

式中，CRTSⅡ轨道板的宽度和高度分别为bc=0.2m，hc=2.55m。根据铁道行业标准[11]已知，单根60kg/m钢轨惯性矩Is为3217cm4，面积As为77.45cm2，轨内中心轴至轨底距离hs为8.12m，代入参数可求得yOU=0.127m，换算截面惯性矩为4.27×10-3m4。

1.2 梁单元非线性几何方程

根据Green-Lagrange 应变张量近似得到截面形心处的轴向应变和曲率分别：

式中，u、v 分别代表轨道的纵向位移和垂向位移。由Duhamel-Neumann 方程[12]得到正应力：

式中，α 为线膨胀系数；EI、EA 分别为截面等效抗弯刚度和等效抗压刚度。

1.3 轨道板与CA 砂浆间内聚力模型

根据刘学毅等[13]通过试验分析轨道板与砂浆层间的粘结关系，采用线性关系来表征轨道板与砂浆层之间的界面阻力，用ks表示单位长度的纵向阻力。

2 温度荷载作用下的解析解

轨道结构失稳屈曲时总势能主要有：弯曲形变能、轴向压缩形变能、砂浆层纵向约束形变能、脱空点纵向阻力形变能及重力势能组成。由于对称性，右半部分结构其总势能方程：

式中，（0,l1）段属于屈曲脱空区域；（l1,∞）段为两侧影响区域；up为脱空点的垂向位移。令δΠ=0，可得脱空区域轴向和垂向的平衡微分方程分别：

式中，温度应变εT=αT，根据式（9）可知，当0＜x＜l1时，轴力为常量，令N1=-EA（εm-εT）。

轨道板纵向由宽窄接缝连接见图3，在屈曲上拱过程中，窄接缝界面因挤压易出现接缝破损，此时下截面重心上移，轨道板将沿垂向将产生偏心受压[14]。

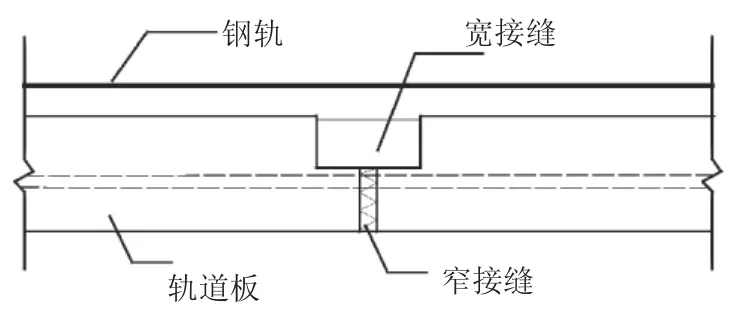
图3 宽窄接缝示意图

由于二阶效应不明显可假定上拱脱空段轴力保持不变，仍为N1，偏心距为e=0.25h（1-E1/E），其中E1为窄接缝的弹性模量，则附加弯矩：

新增项即由窄接缝损伤产生的附加弯曲形变能，同理可得屈曲脱空区域内沿u 方向和v 方向的平衡微分方程分别见式（13）和式（14）：

右侧直板段区域内沿u 方向和v 方向的平衡微分方程分别见式（15）和式（16）：

各段的边界条件也有所不同，对于原点处：

对于脱空点存在变形协调条件，则：

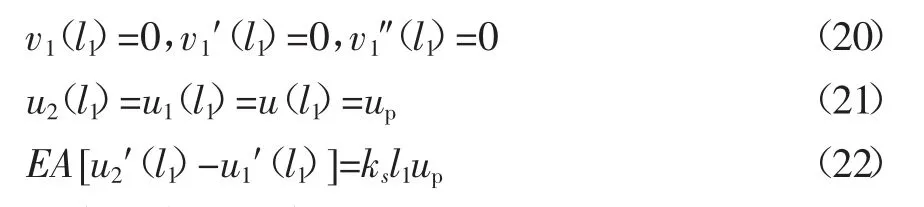
且在无穷远处有：

考虑到式（23）中第二项关于无穷远处的边界条件可知B1=0，故两侧直板段区域的轴向位移：

将式（5）第一项代入式（13）可得脱空区域的轴向位移：

在（0，l1）段内积分，即可得到脱空点伸长的轴向位移：

式（37）的最后一项可通过式（27）积分求得：

将两段轴向位移代入式（22），可以得到脱空点的位移方程为：

3 有限元验证

鉴于目前分析钢轨和轨道板组合结构热致隆起屈曲的研究成果较少，模型验证时采用与其稳定性规律相似的轨道板屈曲计算结果进行对比分析。根据刘笑凯等[15]建立了轨道板垂向失稳的有限元模型，利用abaqus 数值分析软件，建立平面二维有限元模型，轨道板与砂浆层均采用4 节点平面应力单元进行模拟，轨道板两端、底座板两端和底面均采用固定约束。由于不考虑层间粘结，轨道板与支承层之间的关系采用赫兹接触进行模拟，基于risk 法利用迭代的原理分析结构失稳后的平衡路径，得到了有限元模拟结果，与文中能量变分法的结果对比如图4 所示。

图4 解析解和数值解的对比

可见两者计算结果较为吻合，趋势大体一致，得以验证前述公式推导的正确性、可靠性。

4 相关计算参数影响规律分析

4.1 轨道板厚度对稳定性的影响

轨道板厚度对结构安全温度的影响如图5 所示，v1max即为上拱最大位移，将轴力无量纲化，由图5（a）可以看出，厚度增加2 倍时，安全温度提高了55.7%，最大上拱高度提高了39.5%，表明厚度对安全温度的影响非常显著。在图5（b）中，厚度增加到30 cm 时，轨道所承受的最大轴力提高了32.6%，同样表明厚度的增加可提升轨道的安全温度。

图5 轨道板厚度对轨道结构安全温度的影响

4.2 重度对稳定性的影响

钢轨和轨道板组合结构的重度对轨道稳定性的影响如图6 所示。图6（a）可见当重度增加了1.4 倍时，轨道安全温度提升了19.3%。图6（b）表示了无量纲轴力与上拱位移呈单调递减的线性关系，表明随着上拱位移的增加，结构轴力得到释放，脱空距离不断增长。此外，当重度增加了1.4 倍时，临界轴力提升了27.3%。因此，增加轨道重度是提高热荷载影响下轨道稳定性较为有效的方法。

图6 重度对轨道结构安全温度的影响

4.3 窄接缝弹性模量对稳定性的影响

窄接缝是轨道上拱过程中易出现破损的地方，而此处一旦出现破损将进一步增加结构上拱的风险。当窄接缝弹性模量E1分别降低了0%、50%和100%的3种情况下，对应的偏心距e 为0、0.025、0.05 mm。图7分析了偏心距对结构整体上拱的影响，结果表明此时对结构整体失稳影响不大，窄接缝完全失效时，安全温度降低了1.8%，临界轴力降低了1.8%。可以进一步推测窄接缝损伤只在其一定范围内出现较明显的影响，而对结构整体影响较小。但是若要进一步保证结构的安全温度，仍应该着重控制窄接缝的弹性模量、粘结效果等因素。

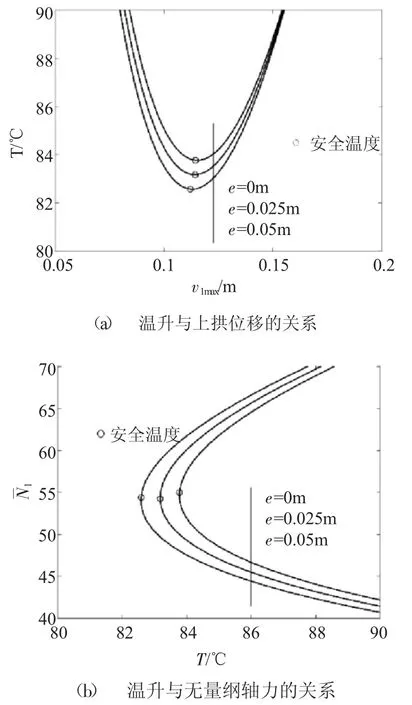
图7 窄接缝破损对轨道结构安全温度的影响

5 结语

（1）利用能量变分原理，列出纵连板式轨道上拱屈曲的总势能方程，结合边界条件得到板式轨道上拱屈曲闭合解，提出稳定性计算公式全过程。

（2）轨道厚度和重度是影响上拱的重要因素，当轨道板厚度增加了2 倍时，安全温度提高了55.7%，临界轴力提高了32.6%；另外重度增加了1.4 倍时，安全温度提升了19.3%，临界轴力提升了27.3%。

（3）当窄接缝完全失效时，安全温度降低了1.8%，临界轴力降低了1.8%，表明其对无限长轨道的整体稳定性影响不明显，但应进一步明确窄接缝破损对其局部范围的影响规律。