基于Matlab的林地作业车臂架轨迹规划

庄徐 郑哲文 李科军

(中南林业科技大学材料科学与工程学院，湖南 长沙 410000)

引言

在我国林区伐木作业领域普遍实现了半机械化[1]，但森林树木的采伐仍然以人工劳动为主，工作强度较大，效率较低。近年来，随着人力成本增加森林作业成本也在不断地增加，如何提高森林作业质量和效率成为人们亟待解决的问题[1]。林地作业车具备快速、准确、多功能等优点[3]，与一般工业机器人相比，其臂架结合机械结构与液压驱动的方式来控制机械手的运动轨迹，能够提升林区作业效率，减轻工人的劳动强度，是林业现代化的重要标志之一[13]。

目前，国内外学者对于运动学分析与轨迹规划进行了深入研究。沈雅琼等[5]运用齐次变换矩阵，建立平动和转动轨迹方程，进行位置和姿态的插补。滕儒民等[6]采用内点法对凸优化模型求解，计算出大高度举高消防车进行轨迹规划的最优解。秦超等[7]利用五次多项式法和摆线运动法对比研究末端执行器的位移和速度，得出五次多项式法较摆线运动法安全性较高。张文典等[9]运用关节空间对六关节臂型机器人进行轨迹规划仿真，并验证该模型能够准确实现机器人关节控制。王智兴等[10]利用MATLAB下的Robotics Toolbox模块建立了运动学模型并验证了运动学方程的正确性。李庆等[11]利用MATLAB与Solidworks对机器人的轨迹进行联合仿真求解，证明正运动学与逆运动学求解的准确性。万正海等[12]利用MATLAB对自建机器人手臂进行轨迹规划仿真，验证了自建机器人手臂设计参数的合理性。Xi[14]应用Bi-RRT算法对冗余机器人进行避障轨迹规划，通过仿真实验验证了能够实现自动避障需求。Zhang等[15]采用SQP算法用于液压机器人挖掘机轨迹规划，验证了相同权重下的SQP方法求解最优解的效率更高，挖掘轨迹更平滑，自主运行变得更加稳定和高效。王宁[16]以六自由度工业焊接机器人为研究对象，运用五次多项式对各个关节进行轨迹规划，得到了各个关节连续平滑的轨迹曲线，有效解决了加速度不连续的问题。虽然相关研究人员在工业机器人领域取得了一定的研究成果，但关于林区工程机械的运动学分析以及轨迹规划仿真仍有较大的开展空间。

本文以曲臂式林地作业车的臂架末端的运动轨迹为研究对象，通过建立D-H坐标系[8]，分析臂架末端在关节空间下的轨迹，在MATLAB环境中实现臂架轨迹的仿真，得到臂架末端相对于基座标系的运动曲线，以及运动中各关节的位移、速度、加速度随时间变化的曲线。为了提高臂架在工作状态下轨迹规划的精确性，本文不考虑升降机构的变化，仅研究林地作业车在升降机构全伸状态下的轨迹规划。

1 林地作业车组成结构

林地作业车需要各臂架的协调运作来实现末端的工作装置具备在林区复杂的工作环境下以指定姿态进行动作的能力，主要由底盘、升降机构、俯仰机构、调平机构和机械手组成，结构简图如图1所示。

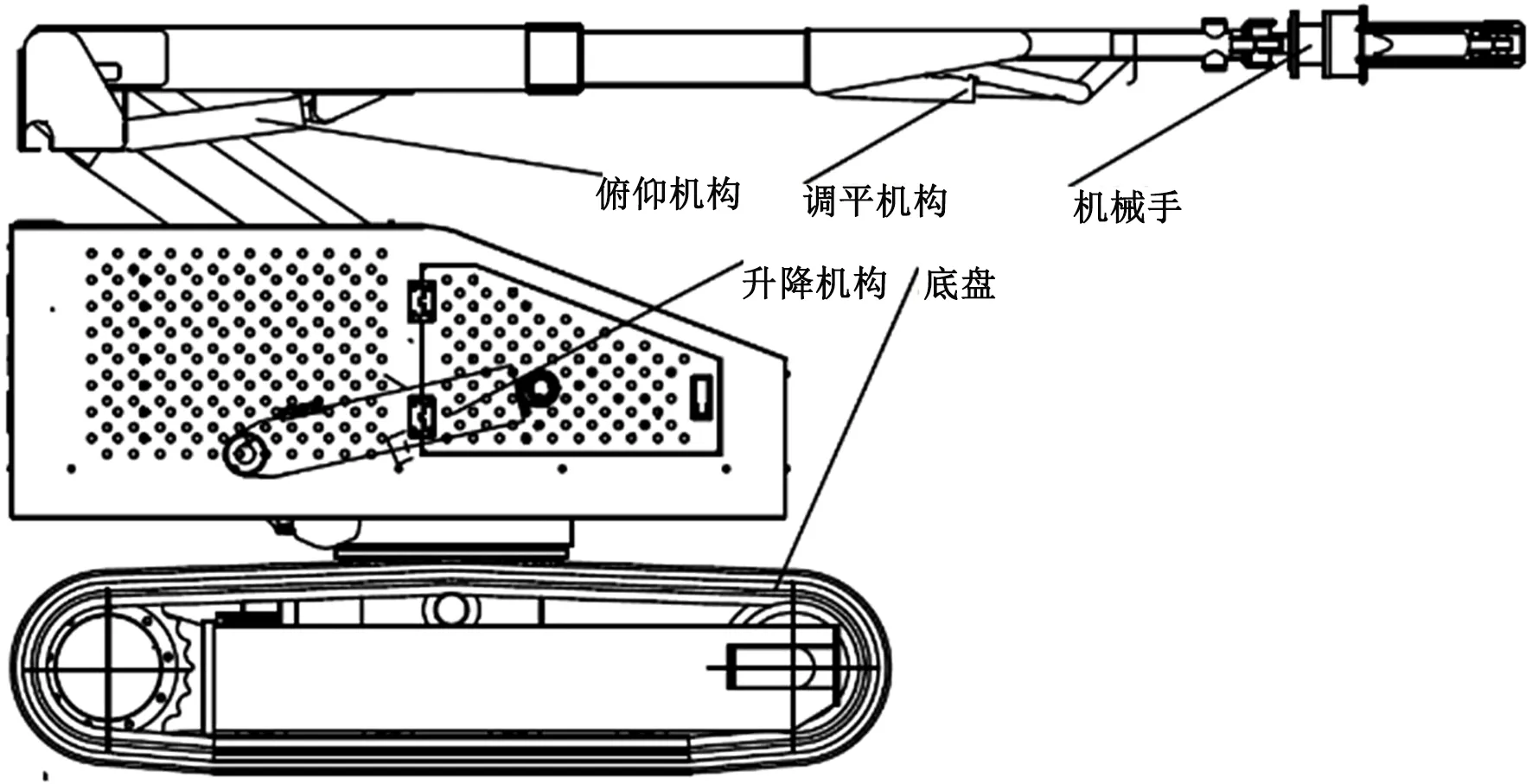
图1 林地作业车

2 林地作业车臂架运动学分析

2.1 正运动学模型的建立

林地作业车的臂架由连接在一起的连杆系统组成，可以将臂架各组成机构简化为4个几何参数，即2个连杆间的夹角θ，2个连杆间的距离d，连杆的长度a以及连杆的转角α。根据标准型D-H参数表示法，建立臂架连杆坐标系，如图2所示，2个连杆之间可通过一个4×4的齐次变换矩阵表示连杆坐标系的变化关系，最终得到末端机械手坐标系相对于基座标系的总变换矩阵。臂架D-H参数如表1所示。

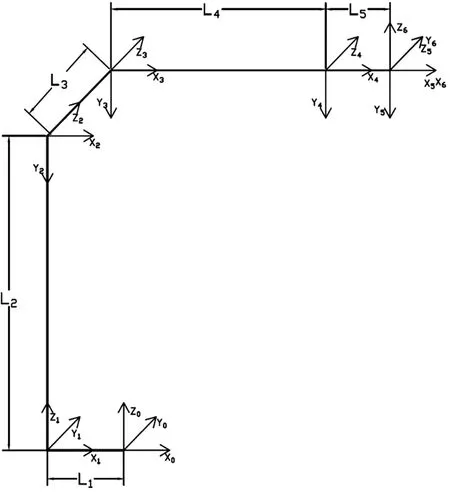
图2 臂架D-H坐标系的建立

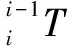
(1)

式中，c表示cos，s表示sin，i=1、2、3、4、5、6。

表1 臂架D-H建模参数

将表(1)中的数据带入式(1)中可得林地作业车各连杆间的齐次变换矩阵：

(2)

由各连杆间的变换矩阵可推导出末端机械手坐标相对于基坐标系的位姿矩阵：

(3)

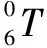
nx=(c1c2-s1s2)[(c3c4-s3s4)(c5c6-s5s6)-(c3s4+s3c4)(s5c6+c5s6)]

ny=(c1c2+s1s2)[(c3c4-s3s4)(c5c6-s5s6)-(c3s4+s3c4)(s5c6+c5s6)]

nz=(c3s4+s3c4)(s5s6-c5c6)-(c3c4-s3s4)(s5c6+c5s6)

ox=-c1s2-s1c2

oy=c1c2-s1s2

oz=0

ax=(c1c2-s1s2)[(c3s4+s3c4)(c5c6-s5s6)+(c3c4-s3s4)(c5s6+s5c6)]

ay=(c1s2+s1c2)[(c3s4+s3c4)(c5c6-s5s6)+(c3c4-s3s4)(c5s6+s5c6)]

az=(c3c4-s3s4)(c5c6-s5s6)-(c3s4+s3c4)(c5s6+s5c6)

px=a1c1-d3(c1s2+s1c2)+(c1c2-s1s2)[(a4+c5a5)(c3c4-s3s4)-s5a5(c3s4+s3c4)]

py=a1s1+d3(c1c2-s1s2)+(c1s2+s1c2)[(a4+c5a5)(c3c4-s3s4)-s5a5(c3s4+s3c4)]

pz=d2-a5(c3s4c5+s3c4c5+c3c4s5-s3s4s5)-a4(c3s4+s3c4)

假设臂架初始状态的关节变量为p=[0,0,0,0,pi/2,0]，调用Toolbox中的fkine()函数可以得到臂架末端坐标系相对于基座坐标系的位姿矩阵，即为臂架的正运动学解。此时由MATLAB计算得到臂架的正运动学解：

(4)

将关节变量p=[0,0,0,0,pi/2,0]代入式(2)中，所得结果与fkine()函数计算求解一致，由此可以验证由MATLAB建立的林地作业车臂架模型的准确性。

2.2 逆运动学分析

2.2.1 关节转角的求解

臂架末端在沿着期望轨迹运行的过程中，需要各连杆的转动协调配合来实现。根据林地作业车臂架的结构特性，关节2和关节3在静止时能够确保臂架末端机械手在工作时与底盘处于垂直状态。因此在工作状态下θ2、θ3总是为0。

根据建立的D-H坐标可知，关节6的坐标由关节5坐标绕x轴旋转而来，关节6的运动相对于关节5的位置不构成影响。因此关节5与关节6相对于基座标系的位姿矩阵相同，即：

(5)

(6)

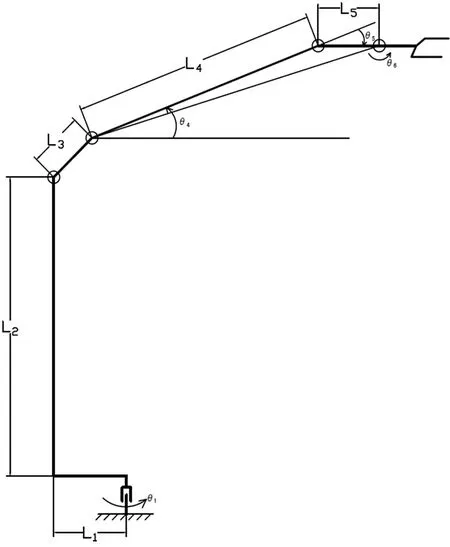
图3 林地作业车臂架关节简图

由图3所示的臂架关节简图可知，可由余弦定理公式计算出θ5,将公式(3)与公式(5)带入可得：

(7)

由于关节6的坐标与关节5的坐标相交于同一点，且关节6的运动不影响关节5的位置，所以关节4的运动不影响关节5与关节6的位置，则：

(8)

(9)

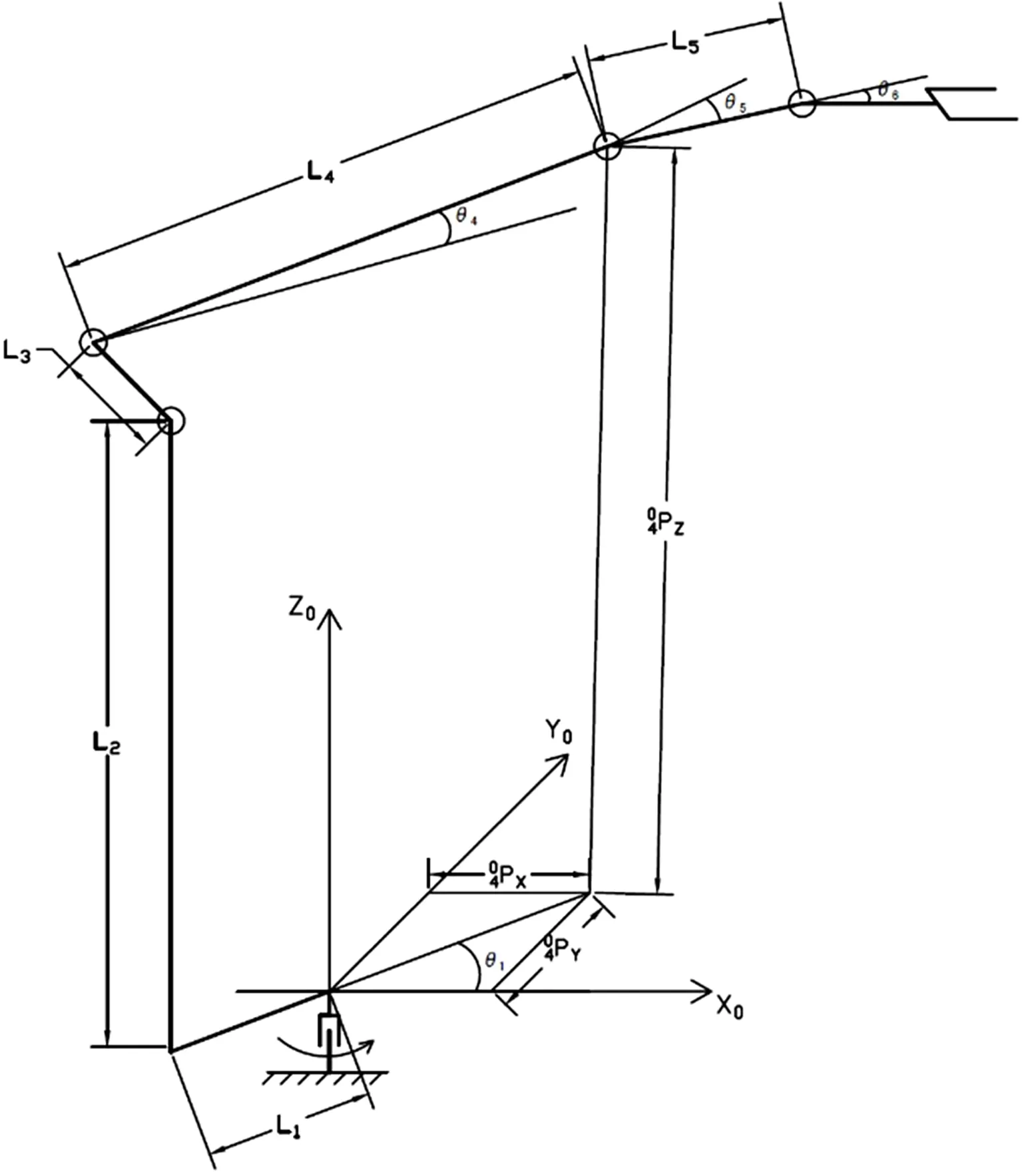
图4 林地作业车臂架关节三维简图

由图4林地作业车臂架关节三维简图中连杆1、连杆2、连杆4的几何关系可知，关节4的位置矩阵：

(10)

将式(9)中各解带入式(10)得：

(11)

化简得：

(12)

(13)

由式(2)可知s6和c6的大小，则可计算出θ6的值：

(14)

综上所述，可通过末端机械手已知的位姿矩阵计算出θ1、θ2、θ3、θ4、θ5、θ6的值，即林地作业车臂架的逆运动学解。

2.2.2 逆运动学的验证

在MATLAB中，调用Robotics Toolbox中的link()函数与Seriallink()函数搭建林地作业车臂架模型，在臂架处于初始状态和工作状态下各关节的角度作为验证数据，利用正运动学公式求解出末端机械手相应的齐次变换矩阵，并将所得的位姿矩阵带入到ikine()函数中，证明逆运动学求解的准确性。臂架在初始状态下和工作状态下各关节转角分别为p1=[0,0,0,0,pi/2,0]，p2=[pi/3,0,0,-pi/6,pi/6,pi/4],得到末端机械手的齐次变换矩阵为T1、T2。

(15)

通过MATLAB搭建的臂架在初始状态和工作状态下的运动学模型如图5所示，根据所得的齐次变换矩阵T1、T2，ikine()函数计算所得的值为Q1=[0,0,0,0,1.57.0],Q2=[-1.05,0,0,-0.52,0.52,0.79]，与臂架各关节转角一致，验证了逆运动学求解的准确性。

ikine()函数计算出的结果与设定的初始关节变量相同，但由于臂架在运动时可通过多组关节变化实现末端机械手到指定位置的路径，其函数求解只是其中一组路径，在进行轨迹规划时则需根据工作环境的情况去求解逆运动学的最优解。

3 林地作业车臂架轨迹规划仿真

将臂架末端机械手作为目标，机械手在工作时经过的若干点即臂架的轨迹。臂架运动时，通过运动学求解计算出各关节的变化规律，结合工作对象选择合适的关节规划出一条光滑轨迹。对臂架进行轨迹规划主要有2种方法，关节空间下的轨迹规划和笛卡尔空间下的轨迹规划。根据林地作业车的结构特征，主要考虑机械手夹取树木时从初始位置至目标位置的轨迹，因此选用关节空间下的轨迹规划较为适用。

图5 林地作业车臂架Robot模型

在关节空间下进行轨迹规划时，首先确定末端机械手的初始位置和目标位置，对初始位置和目标位置进行逆运动学求解计算出各关节所需变化的角度。本文在MATLAB平台中采用五次多项式插值进行轨迹规划。

在RoboticsToolbox中调用jtraj()函数运用到林地作业车模型上，设置初始位置关节转角[-pi/6,0,0,0,pi/2,0],目标位置关节转角[pi/6,0,0,-pi/6,pi/6,pi/6]，步长设置为100，轨迹规划如图6所示。

图6 臂架关节空间下的轨迹规划

各关节的位移、速度、加速度如图7～9所示。

图7 关节位移

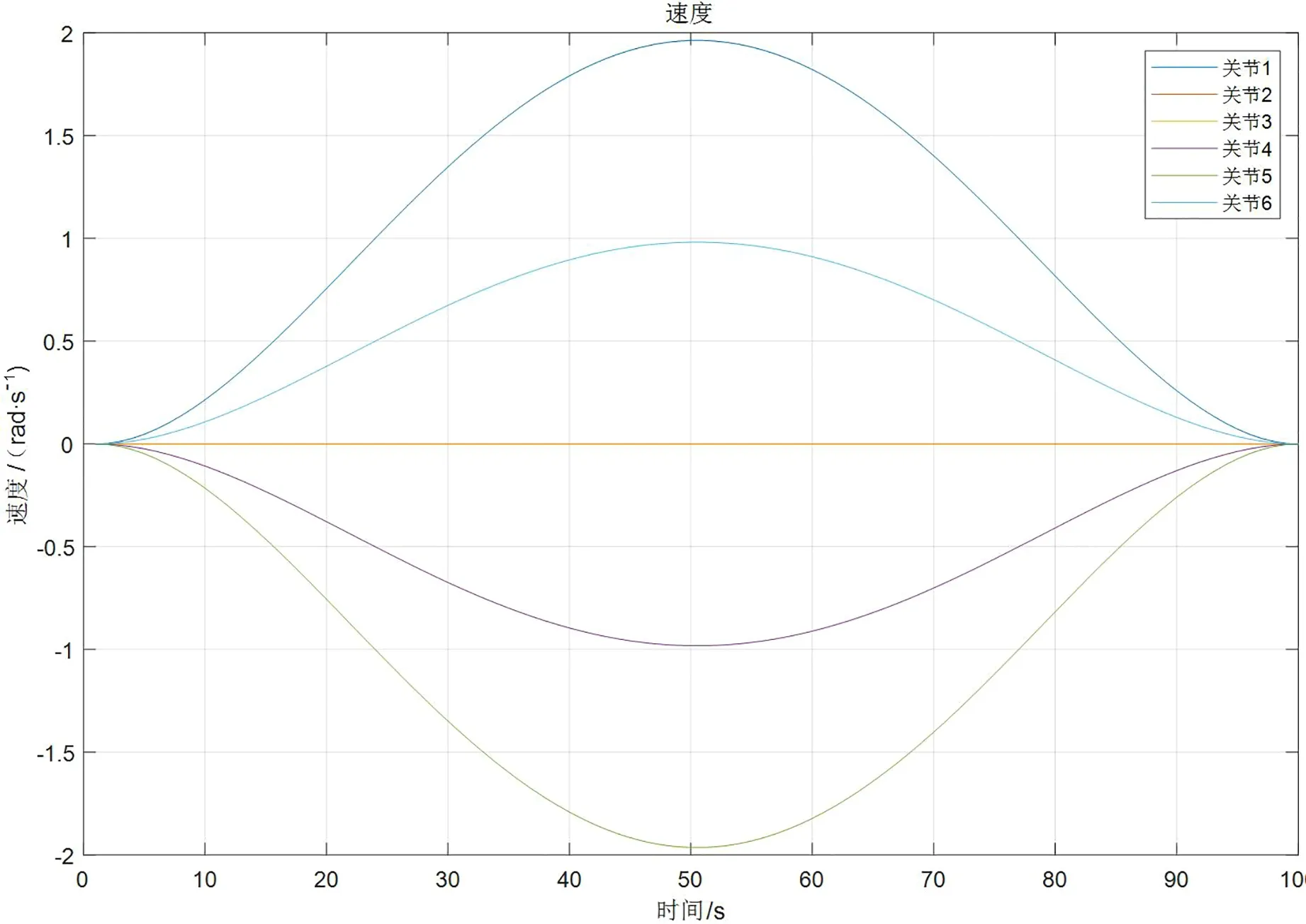
图8 关节速度

图9 关节加速度

分析图7～9可知，臂架在初始位置和目标位置的速度与加速度都为0。在50s时，除关节2和关节3外，各关节加速度为0且速度达到最大值，且关节1与关节5大小相同方向相反，关节4与关节6大小相同方向相反。在运动状态下，各关节的位移曲线光滑、均匀，且各关节的速度没有出现剧变，说明臂架各关节在工作时较为稳定，没有出现明显振动。

4 结论

本文根据林地作业车六自由度臂架的结构进行了运动学分析，采用标准型D-H法建立臂架连杆坐标系，完成了臂架各关节正逆运动学求解，通过MATLAB软件验证了正逆运动学模型的准确性。

通过对臂架各关节正逆运动学求解分析，得到了各关节和末端机械手的位姿之间的齐次变换矩阵。

运用MATLAB软件对林地作业车的臂架进行了运动学仿真和轨迹规划，各关节的位移、速度、加速度随时间变化的曲线光滑、连续，验证了臂架各关节在运行过程中的稳定性。