基于表面硬度的隧道围岩强度快速测试方法研究

陆学元 程华才 徐 良 马子宸 郑睢宁 陈华鑫 关博文

(1.安徽省交通控股集团有限公司 合肥 230088； 2.安徽省高速公路试验检测科研中心有限公司 合肥 230601； 3.长安大学 西安 710064)

0 引言

随着交通事业的快速发展，隧道工程的建设越来越多，在隧道建设过程中，由于隧道施工使得周围岩体受到开挖影响而发生应力状态改变，围岩的稳定性对隧道工程来说是不言而喻的，所以在隧道施工中最关心的问题就是地层被挖成隧道后的稳定程度。因为地层稳定就意味着开挖隧道所引起的地层向隧道内的变形很小，而且在较短的时间内就可基本停止，有利于后续施工；如果稳定性不佳，则会加大后期维护费用，并且对施工安全埋下隐患，因此隧道围岩的稳定对施工过程和支护结构都是非常有利的。

隧道围岩强度是否满足施工需要是一个十分重要的问题[1-2]，但是在施工现场对围岩的快速检测依旧不成熟，因此对岩石方面的探究就尤为重要。然而在现场施工过程中，因为各个标段岩石风貌不同，导致岩石自身性质差异较大，对测量其围岩硬度有较大的影响，有时因为测量硬度时方法不当导致对围岩硬度没有准确评价，影响对隧道围岩强度的判别，为整个施工过程埋下安全隐患。

由于母岩所处位置不同，对测量条件也有影响，导致无法对母岩的所有表面做出测量，因此目前尚无有效手段可对母岩整体强度进行检测。测试其表面硬度主要靠硬度仪，因为现场施工环境受限，所以里氏硬度仪作为测试硬度的仪器，有较好的便携性，方便野外测量。硬度不是一个简单的物理概念，而是材料弹性、塑性、强度和韧性等力学性能的综合指标。林鹏等[3]通过一种岩石单轴抗压强度预测系统与方法，将岩石回弹测试模块用于对岩石的回弹测试，并输出岩石的单轴抗压强度预测结果。Celik[4]利用回弹基硬度测试方法来预测岩石材料的物理力学性能,对里氏硬度与岩石的物理和力学性质关系进行预测。曾伟雄等[5]设计了求岩石单轴饱和抗压强度的两种点荷载试验方法,并与室内抗压强度试验结果进行了对比，但这些试验测量仅限于在实验室环境下进行，在工程现场，由于条件限制，更需要一种快速便捷的测定方法。

鉴于此，本文对围岩表面的里氏硬度值及其抗压强度建立关系，可以在工程现场使用简单便捷的方法对围岩硬度进行判定，以确保隧道围岩的质量安全。

1 原材料及试验方法

1.1 试验材料

隧道围岩部分选取来自安徽的石灰岩(简称SH)与花岗岩(简称HG)两个不同的岩石样本作为测试对象，通过X射线衍射(XRD)对岩石矿物组分进行分析，结果如表1所示。

表1 岩石矿物组成

本文采用吉泰科仪生产的JITAI.771里氏硬度计进行测量，并按照《金属里氏硬度试验方法国家标准编制说明》GB/T 17394—1998[6-8]测试标准进行硬度值测量。测试时应避开裂缝处与岩石变异结晶处，这会对测试结果产生较大的误差，也不能准确反映其真实的表面硬度值。测量时应选取岩石表面较为平整的一面，且保证母岩表面结构完整、致密，无明显裂纹，符合所测试验准备要求。

抗压强度测试试验。为了探究岩石表面的里氏硬度值与其自身抗压强度大小的相关程度[9-10]，将母岩切割成70mm×70mm×70mm的立方体试件，并使用DYE-2000型的恒应力试块压力机，对试块进行压力测试。

1.2 表面硬度测试

目前测试硬度计主要有以下几种：布氏硬度计多用于半成品的测量，测试时会对被测物体表面造成较深压痕，且操作较为复杂；维氏硬度计适用于较薄的维氏硬度值测量,对于试样表面的光洁度要求较高,通常需要制作专门的试样；洛氏硬度计测量最为精准，但是体积较大，只能在固定实验室测量，对工件的大小有限制；里氏硬度计是便携式硬度计，体积小巧，方便操作，但干扰因素较多，示值稳定性不好，适合于现场对岩石的快速检测[9,11]。为了减小干扰因素的影响，对最小测量数有一定要求，以保证测量结果的准确性与可靠性。

为了探究岩石表面的里氏硬度值与其自身抗压强度的相关性，本文采用里氏硬度计对其表面里氏硬度进行测试，获得表面里氏硬度的分布规律并进行数据处理，制定获取可靠表面里氏硬度代表值的方法，研究岩石表面硬度的表面里氏硬度与其抗压强度的相关性。里氏硬度计[5,12]主要工作原理是弹性冲击原理，工作过程是将装置内的碳化钨冲击体从卡槽处释放，撞击在所测物体表面，通过将重力势能转化为弹性势能，获得回弹速度，通过数量转换即反弹速度与冲击速度之比得到里氏硬度值，其主要原理是利用物体表面的强度与其自身抗拉强度的相互作用关系。

2 结果与分析

2.1 里氏硬度测试结果

2.1.1 试验结果误差分析

由于里氏硬度试验的影响因素很多，因此在不同方式环境下所测得的原始数据中出现明显偏离各自平均值的个别零散数据值是正常的现象，因为在试验过程中对误差影响因素无法完全进行判别，所以使用数学统计中的拉依达准则进行了数据筛选。如果对某测量值xp有残vp=xp-¯x，当|vp|>3S时，则认为xp含有较大测量误差应被剔除。8组数据中有两组数据存在异常点，剔除异常点后计算各组数据的平均值、标准偏差和变异系数结果见表2。

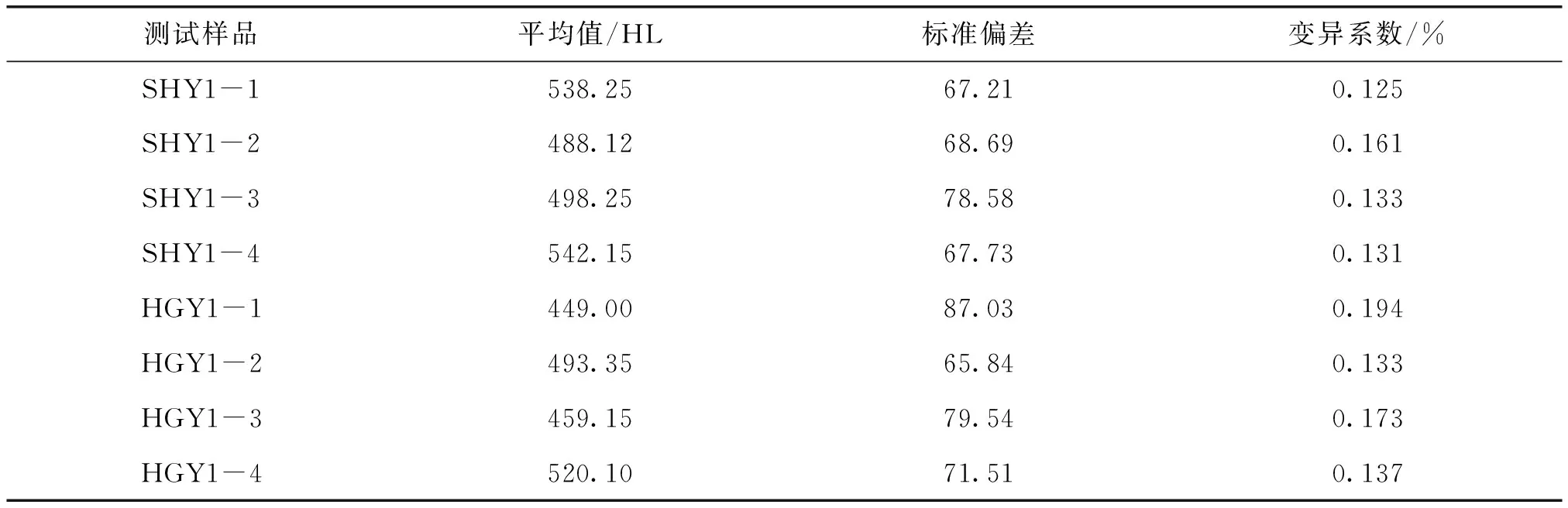
表2 样品测试后的计算数据

2.1.2 试验结果统计分析

对所测母岩表面的里氏硬度值进行统计分析结果见图1，由图1可见：SH与HG的表面里氏硬度数据分布有相同的趋势，并可以看出各组数据的正态分布拟合度很高，且都呈现以均数为中心、左右对称，并且正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降，形成一段光滑的曲线，这说明本次试验中岩石表面的里氏硬度值数据可靠；数据的随机误差也在其合理范围内波动，对整体数据的准确性不构成影响，并且服从正态分布，说明该种测试的里氏硬度值具有可行性。

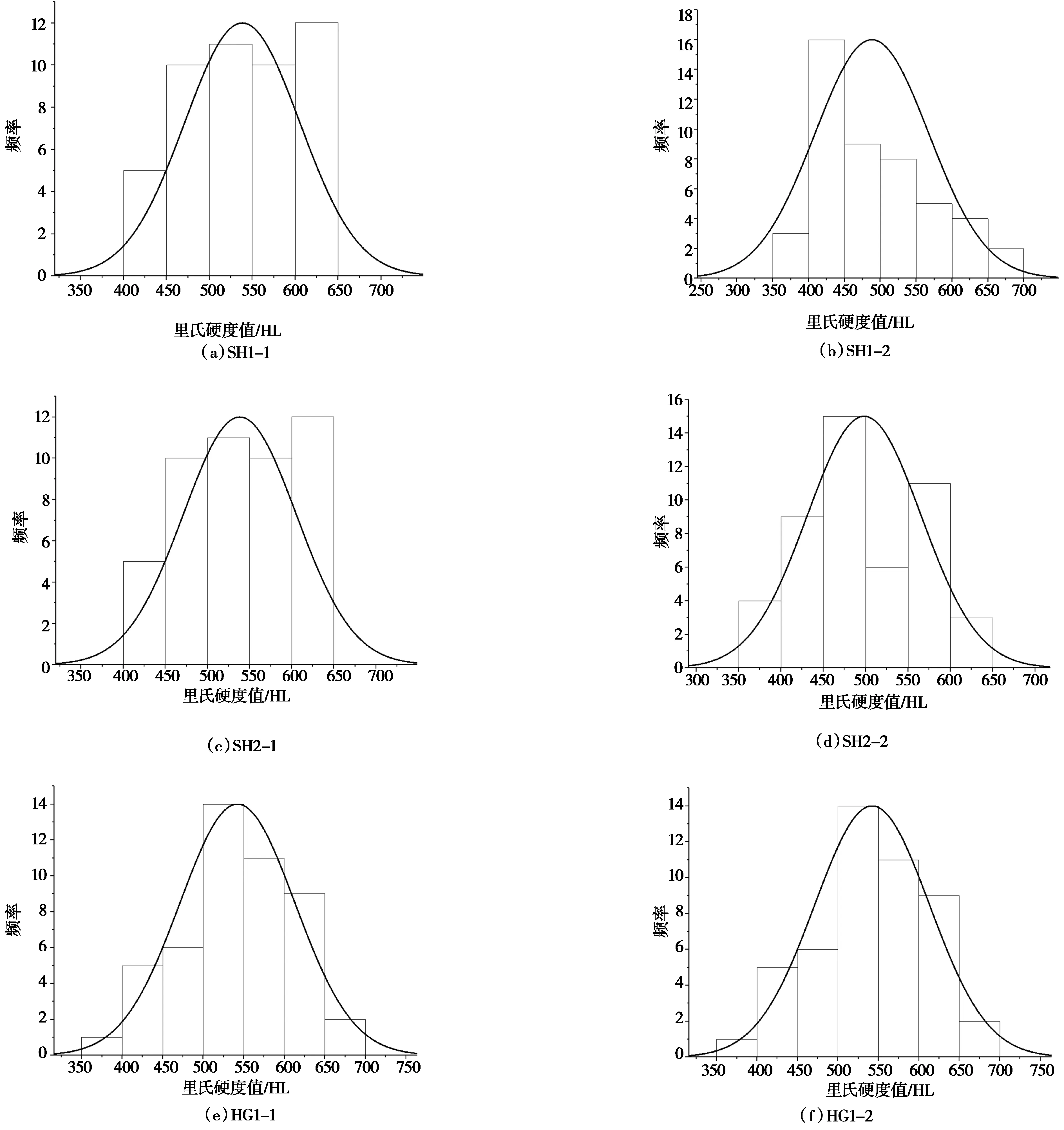
图1 岩石表面里氏硬度分布柱状图

2.1.3 最小取样数量的确定

测定岩石表面的里氏硬度值时，测试点的数量对结果影响较大。测试过程中如果测点数过多，虽然会降低所测数据的离散性，但最终数据与实际数值保持基本一致，这样往往会增大工作量，降低工作效率，影响试验进程；如果所测点数过少，由于数据不全面，且岩石表面凹凸不平出现测量误差几率增大，导致硬度均值的离散性过大，使试验数据误差较大，导致里氏硬度均值的离散性也大，降低数据的可靠性。所以，首先需要确定出合适的最小测点数，以保证数据可靠的前提下，提升测量效率。

测定母岩表面硬度时，如何确定测点数是一个重要的问题。测点数过少时，由于数据不全面，且岩石表面凹凸不平出现测量误差几率增大，导致硬度均值的离散性过大，使得硬度测量数据可靠性大大降低;但测点数过多时，将会使得工作量大幅提升，且降低检测效率。综合文献[14-17]分析，有必要确定一个合理的硬度测点最小取样数量。分别按取样点数 6、9、14、18、24、30、38和48对以上母岩表面强度进行试验[18]，统计其硬度的均值μ、标准差s和离散系数η。当硬度测点取样数量小于30时，硬度的均值μ、标准差s和离散系数η有较大的波动，取样数量30～48时，整体波动较小。所以在确定母岩表面硬度测量数时，不小于30组(图2～图4)。

图2 岩石表面硬度平均值

图3 岩石表面硬度方差值

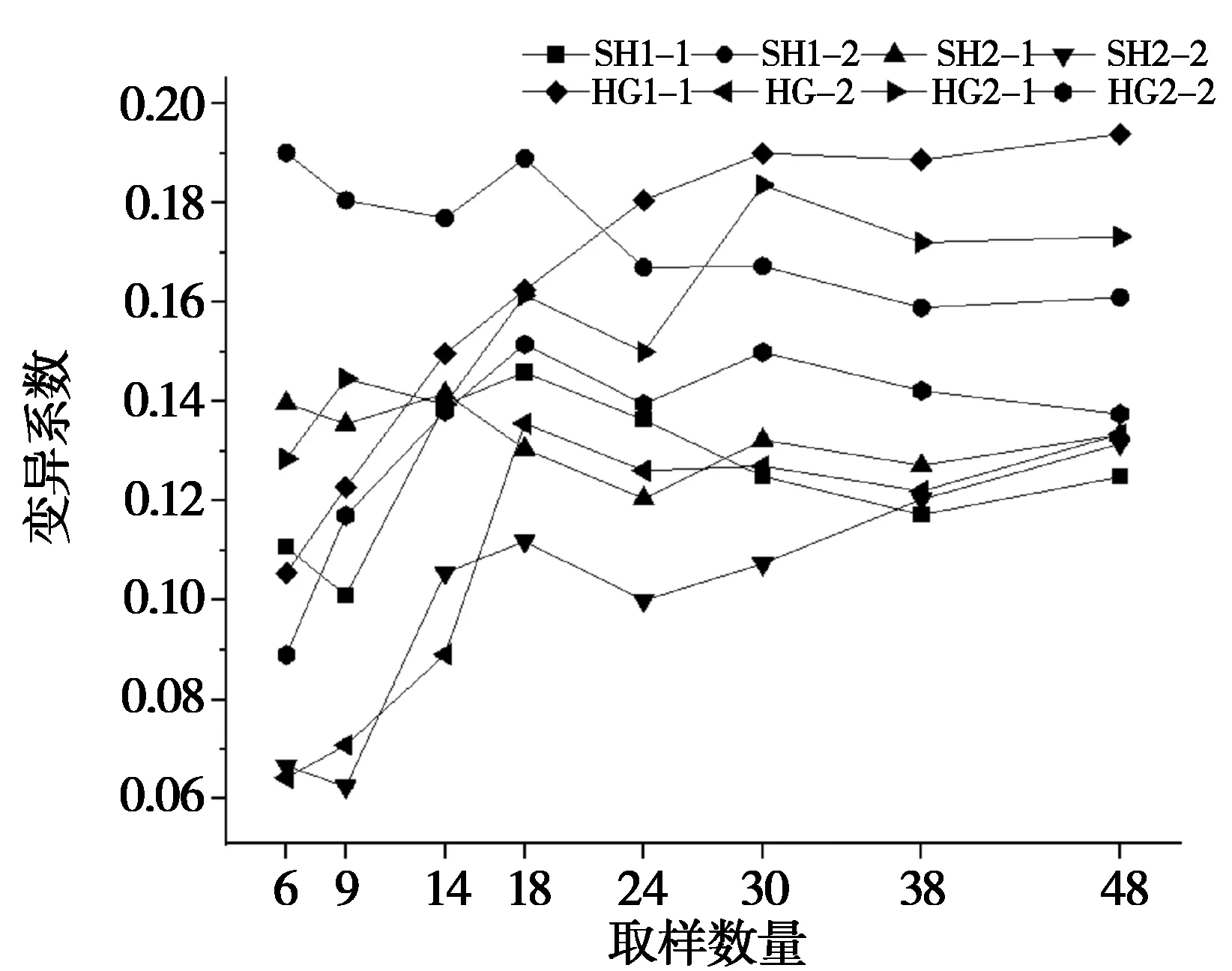
图4 岩石表面硬度值变异系数

从图2可以看出，整体平均值的发展趋势呈平稳发展的状态，开始部分岩石表面硬度值有小幅下降，则是因为岩石表面出现变异部分，且变异部分的硬度值与岩石硬度值不同，导致硬度值的平均值出现这种情况。测点数为6～18时，变化幅度较大，所以不能作为参考数据，当测点数达到30之后，整体曲线发展趋势开始出现缓和部分，此时的误差影响较之前部分呈现减小趋势。

根据图3可以看出，整体的方差曲线变化幅度较大，尤其是在前半部分的6～18点处，8组数据的方差数基本呈现上升的趋势，随着测点数逐步增大，在每片区域的测点数达到30以上时，曲线部分开始出现平稳，且重合度很高，可判断此测点数之后数据趋于稳定。

由图4可知，尽管变异系数和标准差都是表示离散程度的，但是由于两种岩石的组成成分不同，使用变异系数更能反映出该段数据变化的离散程度。在数据的离散系数变化范围中，在开始段6～18部分变化较为剧烈，此段范围的标准差值变化较大，证明此段的数据变化不能表征整体岩石硬度的里氏硬度真实值，当测点数达到30点以上时，变异系数整体变得平缓，此段数据真实度较高。

综合图2～4，试件表面里氏硬度的均值m、样本标准差s和离散系数η在测点数>30次后，各图形都趋于平缓，基本趋于稳定，符合试验目的,因此，最小取样数为30，当样本数>30以后，整体的图像波动随着样本数的增加持续减弱[19-20]，表明如果当测试样本数量足够大时变异系数趋于稳定。变异系数与岩石组成有直接关系，在进行不同岩石的测定时，稳定的变异系数是对其指标合理性的一个重要指标。

3 结论

针对目前无法建立快速的岩石表面里氏硬度值的测定，提出基于对其自身数据正态分布的特点，确定最小测点数，通过建立拟合曲线，确定了硬度值与抗压强度的关系系数，进行分析后得到以下结论：

(1)根据拉依达准则对所测数据值进行判断，384组数据中异常数值仅有2组，占比仅为0.52%，则可以得使用出里氏硬度计对母岩硬度的测量十分契合。

(2)使用不同次数的测试量对其里氏硬度值进行测试，各组图像都符合正态分布，证明所测数据的可靠性较高，并通过均值、样本标准差和离散系数的图像，对试件测试的最小点数确定为30。

(3)本研究采用里氏硬度法对岩石表面的里氏硬度值进行测试，满足了在施工现场条件较为简陋的情况下，也可以拥有较高的准确性。同时，试验结果证明这种方法具有适应小截面、操作便捷且检测误差小等优势，可为类似地母岩硬度的快速检测提供科学参考。