鄂尔多斯盆地东南缘煤岩吸附模型适用性研究

刘友南 邓春涛 梁 博 封宇博

(1.西安石油大学地球科学与工程学院，陕西 710065；2.西安石油大学陕西省油气成藏地质学重点实验室，陕西 710065)

1 地质概况

鄂尔多斯盆地东南缘是我国煤层气含量较高的区域，其中又以韩城区块和大宁吉县区块煤层气产量较高。韩城区块构造上位于鄂尔多斯盆地渭北隆起东北部，构造相对简单，整体为一走向北东-南西、向北西方向倾斜的单斜构造，其主要含煤地层为下二叠统太原组和山西组。大宁-吉县区块隶属晋西挠折带南端，受中部桃园断裂影响，形成“一隆一凹两斜坡”的构造格局。区块内含煤地层自石炭纪开始沉积，形成石炭-二叠系含煤层系，煤系地层后期演化主要受印支运动、燕山运动及喜马拉雅山运动三期构造运动的影响。其深层煤层气勘探区位于西部斜坡带上，主要发育二叠系太原组8号煤层和山西组5号煤层，8号煤层厚度较大，是深层煤层气主要勘探目的层，煤演化程度高，以贫煤、无烟煤为主。

2 研究区煤岩不同吸附模型的建立与比较

煤吸附甲烷的能力相差甚大，是由于煤对甲烷的吸附受多种因素控制或影响，控制或影响因素有：煤变质、煤岩成分、孔表面积、孔体积、水分、压力、温度等。鄂尔多斯盆地东南缘是中高煤阶煤层气富集区，生产煤层气的主力煤层都是中高阶煤，本文针对鄂尔多斯盆地东南缘研究区，优选了以下三种模型进行煤岩吸附模型适用性研究。

为确保实验数据的准确，方便不同模型模拟结果的比较，本文引用了国内学者马行陟针对鄂尔多斯盆地韩城地区进行中高煤阶煤储层吸附能力研究时的煤样数据及相应的等温吸附实验数据，样品信息详见表1。

表1 韩城区块样品信息

2.1 Langmuir吸附模型

1916年美国科学家Langmuir提出了单分子层吸附理论，其数学表达式为：

V=VLP/(PL+P)

(1)

式中：VL为Langmuir体积，反映吸附剂的最大吸附能力，与温度、压力无关，取决于吸附剂和吸附质的性质，m3/t；PL为Langmuir压力，代表吸附量达到Langmuir体积一半时所对应的气体压力，MPa。Langmuir体积(VL)和Langmuir压力(PL)的值可根据等温吸附实验数据进行非线性拟合求得。

如图1所示，Langmuir吸附模型能够与实测值高度契合。因此，Langmuir吸附模型作为表征吸附量与压力相关的最基础的一种模型，在预测煤层气吸附量方面得到了广泛的应用和发展。但是Langmuir吸附模型仅考虑了特定温度下压力对吸附量的影响，无法预测除等温实验设定的温度以外的温度对吸附量的影响。

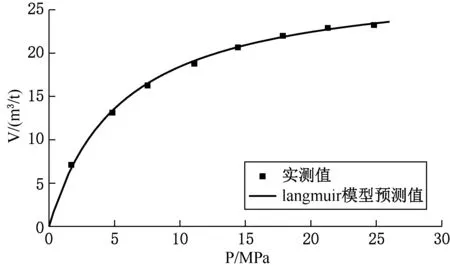
图1 煤样(H6)在90℃条件下Langmuir吸附模型预测吸附量与实测值比较

2.2 温度-压力综合吸附模型

第九届国际煤层气论坛上，我国学者张群根据吸附势理论，从煤的甲烷吸附势与吸附量之间呈现的自然对数函数关系入手，推导出煤吸附甲烷的温度-压力综合吸附模型，其数学表达式为：

lnV=mRTlnP+lnD-mRT[lnPc+k(lnT-lnTc)]

(2)

式中：V为甲烷气体吸附体积，m3/t；m和D为吸附特征常数；T为平衡温度，K；P为甲烷气体平衡压力，MPa；R为气体常数，R=8.31；k为经验系数，k=2.7；Pc为甲烷气体的临界压力，Pc=4.59MPa；Tc为甲烷气体的临界温度，Tc=190.55K。

为使用方便，温度-压力综合吸附模型可以简化为如下形式：

lnV=alnP+b

(3)

式中：a和b为待定系数。

结合样品在某一温度条件下的等温吸附试验结果，计算不同平衡压力及相应吸附量的自然对数值，求出它们的相关关系式(3)，确定a和b的值。对照式(2)，便可计算出各个样品在该温度条件下温度-压力综合吸附模型中的特征常数m、D的值。再将计算出的m和D值带入式(2)，可得到该样品具体的温度-压力综合吸附模型，也就可以计算其他温度条件下不同压力时煤对甲烷的吸附量。

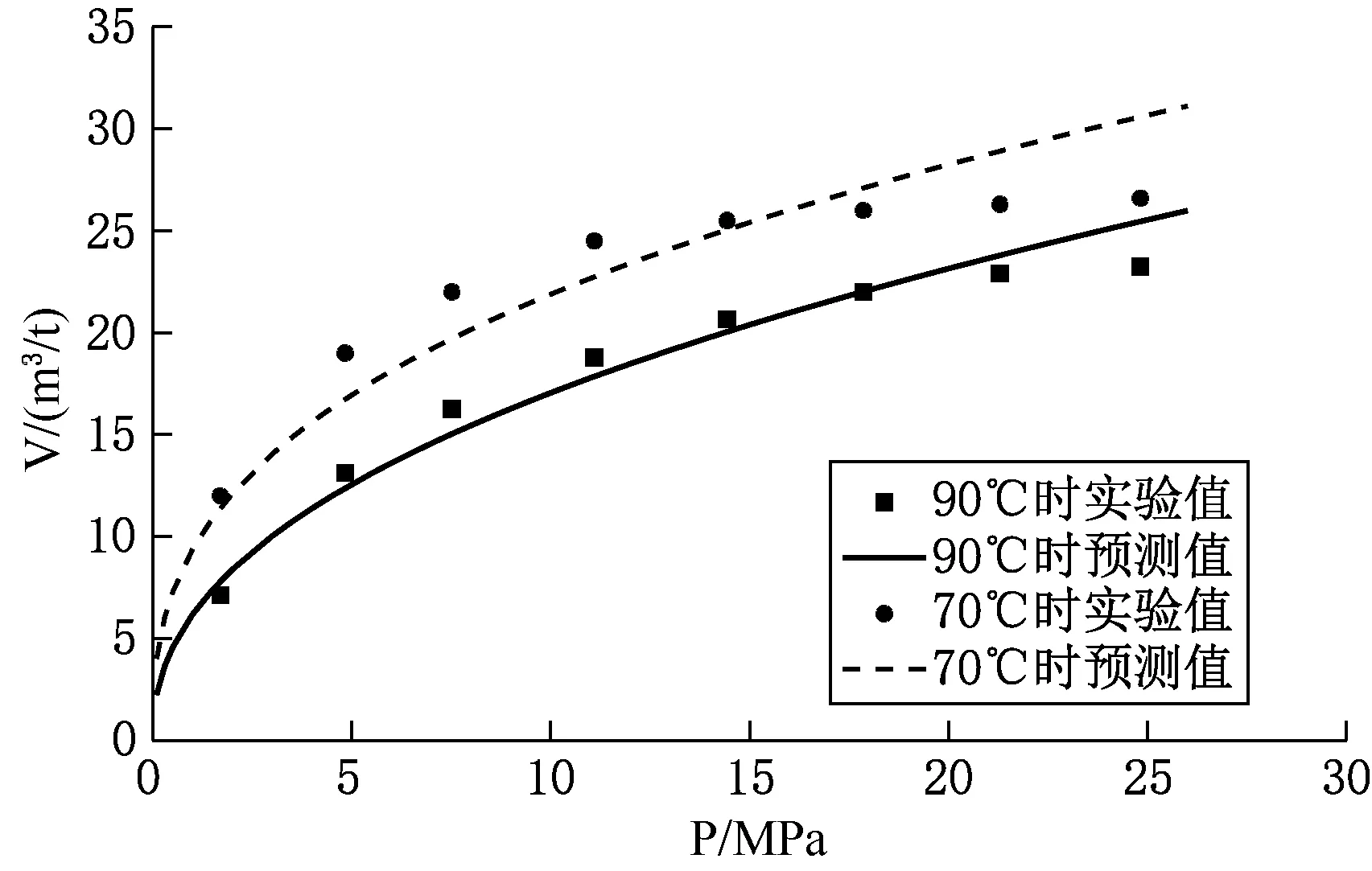
图2 煤样(H6)在90℃(363.15K)条件下所得温—压综合吸附模型预测吸附量与实测值比较

由图2可知，该条件下温度-压力综合吸附模型预测效果没有Langmuir吸附模型好，其中在煤样吸附体积达到Langmuir体积VL之前该模型预测值与实测值比较接近，当煤样吸附量达到Langmuir体积VL之后该模型预测值与实测值偏差较大，且偏差随着压力增大逐渐增大。

虽然温度-压力综合吸附模型达不到Langmuir吸附模型那么高的精确度，但在缺乏实验数据的情况下可根据现有的等温实验数据建立温度-压力综合吸附模型去预测除等温实验设定的温度以外的温度下压力对吸附量的影响。又由于煤岩的吸附能力受多种因素控制，当煤样处于不同温度环境中实验时，煤样其他控制吸附能力的影响素会发生相应变化。所以，当用温度-压力综合吸附模型预测其他温度对吸附量的影响时，若要预测的温度与求取该模型所用的等温实验设定的温度偏差越大，那么预测吸附量与真实值相差越大。因此，建立煤岩吸附模型时应尽可能多考虑控制煤岩吸附能力的因素。

2.3 温度-压力-煤阶三参数吸附模型

2014年国内学者马行陟在Langmuir吸附模型的基础上通过单因素分析建立了Langmuir体积VL的两种指数模型如式(4)所示，同时也建立了Langmuir压力PL的两种双参数的指数模型如式(5)所示，并利用SPSS 19软件进行样品数据回归得到具体的Langmuir体积和Langmuir压力的公式，最后代入式(1)得到三参数煤岩吸附模型。

(4)

(5)

式中：a、b、c、d为待定系数；T为温度，℃；Ro为镜质体反射率。

参照上述分析方法，为求得更为精确的模型，本文利用MATLAB软件对样品实验数据按照式(4)和(5)中的模型重新进行了多变量非线性回归分析：

由图3可知，用Langmuir体积VL与煤阶Ro、温度T的相关关系数据进行拟合，(a)的拟合结果要明显好于(b)，所以实验数据更符合式(4)中的模型I，此时a=2.809，b=-0.01141，c=1.185。

图3 Langmuir体积VL与煤阶和温度的关系

同理，用Langmuir压力PL与煤阶Ro、温度T的相关关系数据进行拟合，虽然对式(5)中的两种模型相关性都不高，但模型Ⅱ的相关性好于模型Ⅰ，此时a=1.215，b=0.01478，c=0.0000002384，d=5.553。

再将VL、PL各自与Ro和T的函数关系带入式(1)可得到以下温度-压力-煤阶三参数吸附模型：

(6)

如图4所示，该条件下，温度-压力-煤阶三参数吸附模型预测的吸附量能够与实测值保持高度一致。该模型既达到了Langmuir吸附模型的准确性，又满足温度-压力综合吸附模型的普适性。但是，温度-压力-煤阶三参数吸附模型的建立需要较丰富的数据支撑，且数据越全面模型越精确。

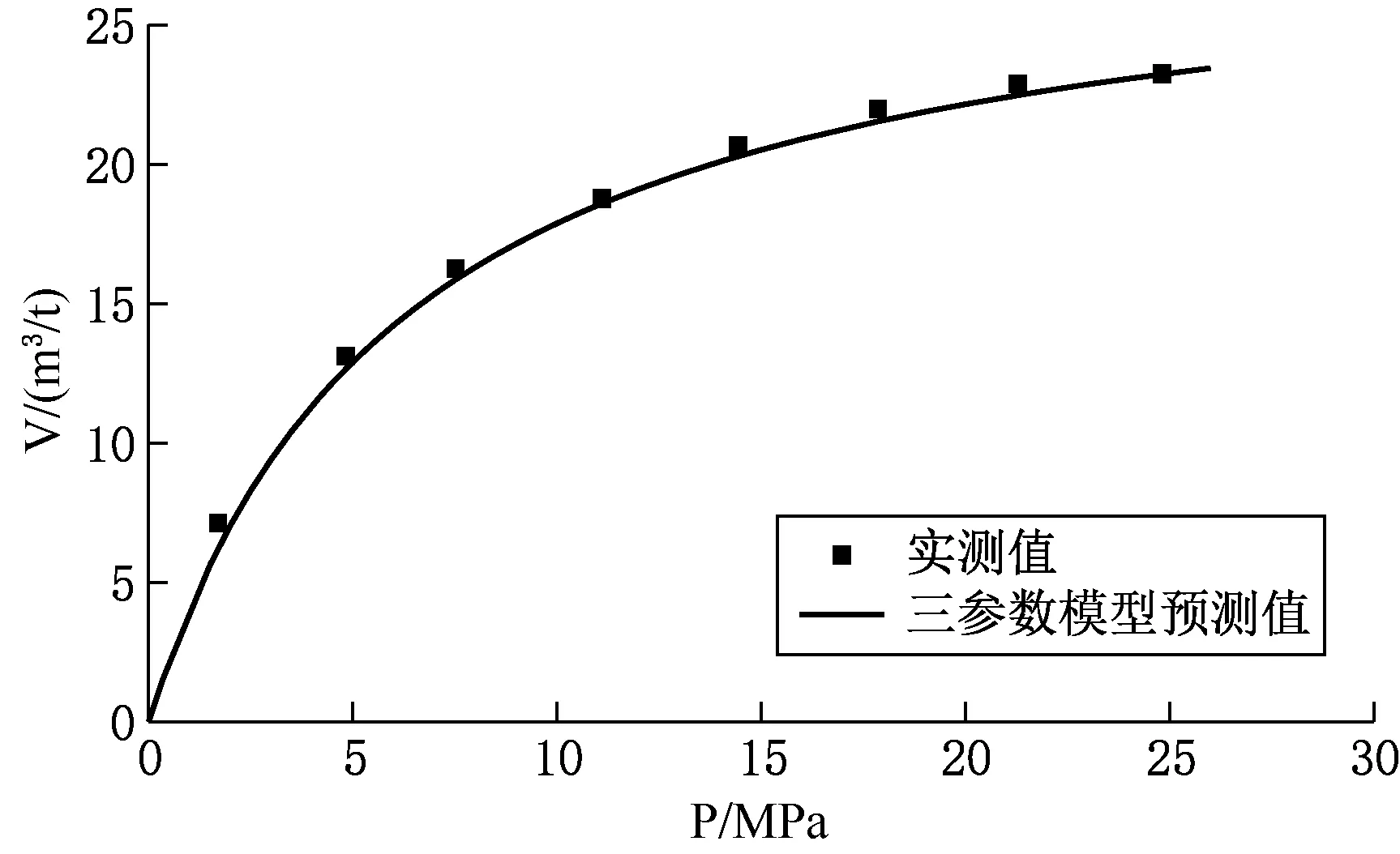
图4 煤样(H6)在90℃条件下三参数吸附模型预测吸附量与实测值比较

综上所述，在煤岩等温实验未能做到全覆盖的基础上，也考虑到节约实验成本的需要，温度-压力-煤阶三参数吸附模型更适用于研究区煤岩吸附能力的定量计算和预测。

3 吸附模型的可靠性检验与应用

3.1 吸附模型可靠性检验

鉴于三参数吸附模型是由研究区多组实验数据拟合得到的温度-压力-煤阶三个参数共同控制煤岩吸附能力的精确表达，将该模型用于研究区的煤岩吸附能力的定量计算应该是非常可靠的。为验证温度-压力-煤阶三参数吸附模型对深层煤层气吸附的适用性，取大宁—吉县区块某井深层煤样并测其等温吸附实验数据，再将预测值与实测值比较便可看出该模型是否适用。样品信息如表2所示。

表2 大宁—吉县区块样品信息

如图5所示，对所取煤样来说，温度-压力-煤阶三参数吸附模型在如图所示温度及压力条件下的预测值与实测值有较高的一致性，在一定程度上该模型可满足定量计算和预测深层煤岩吸附能力的需要。且对于深层煤层气的生产开发来说，此模型可以在难以取得岩心的情况下用较少岩心的实验数据来预测深层煤岩的吸附能力。

图5 大宁—吉县区块煤样不同条件下三参数吸附模型预测吸附量与实测值比较

3.2 吸附模型的应用

本文基于Petromod三维盆地模拟软件对研究区内大宁—吉县区块8号煤的埋藏史、热史等进行模拟，再结合温度-压力-煤阶三参数吸附模型来实现对大宁—吉县区块深层8号煤的吸附史恢复。其中研究区剥蚀厚度的恢复参照了陈瑞银建立的剥蚀厚度恢复模型，通过调试使模拟Ro值与实测值达到最佳拟合效果，来最终确定各个时期的剥蚀量；边界条件的设置则借鉴了前人研究成果，模拟结果如下图所示：

如图6所示，根据研究区8号煤埋藏史、热演化史模拟结果，结合温度-压力-煤阶三参数吸附模型，可定量刻画研究区8号煤自沉积形成至今各时期吸附能力的变化，为该区域深层煤层气的开发研究提供了有效方法。

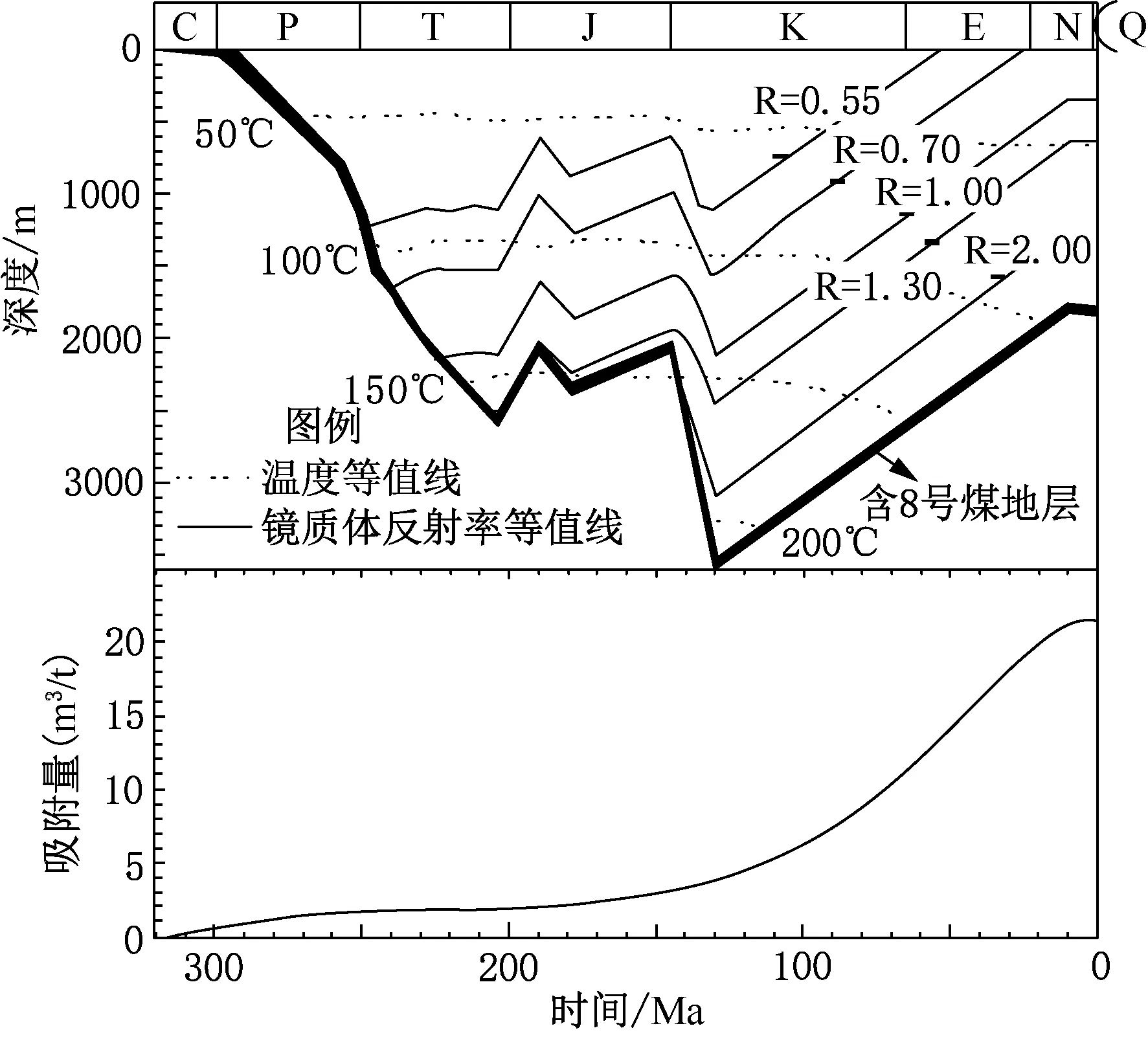
图6 研究区8号煤埋藏史、热演化史及吸附史模拟结果

4 结论

(1)Langmuir吸附模型以其精确的预测结果可作为表征吸附量与压力相关的最基础的一种模型，但仅能预测特定温度下压力对吸附量的影响。

(2)温度-压力综合吸附模型可用于预测除等温实验设定的温度以外的温度下压力对吸附量的影响，但精度不及Langmuir吸附模型。

(3)针对本文研究区块，温度-压力-煤阶三参数吸附模型预测的吸附量能够与实测值保持高度一致，与其他模型相比更适用于煤岩吸附能力的定量计算和预测，但是该模型的建立需要较丰富的数据支撑。

(4)基于Petromod三维盆地模拟软件，温度-压力-煤阶三参数吸附模型在大宁—吉县区块8号煤吸附史恢复上具有良好的适用性。