无监督特征选择的改进稀疏主成分分析算法

范九伦，李维昊，罗绪瑞，支晓斌

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

在计算机视觉、数据挖掘、模式识别和机器学习领域的人脸识别、基因数据分析等应用中，输入的数据集位于数千维度的观测空间中，高的数据维数限制了很多实际应用，直接分析高维数据不仅计算成本高，处理难度也较大[1-5]。同时，伴随数据维数增高，原数据中噪声数据可能会显著增加，导致对数据分析的结果出现偏差。因此，高效处理高维数据已成为亟需解决的问题。大量研究表明，降维是高维数据分析和处理的重要途径之一。20世纪80年代Svante 首次提出主成分分析[6](Principal Component Analysis,PCA)，并将其用于数据降维。PCA作为非常流行的无监督数据处理与降维方法，其主要思想是将n维数据特征映射到k维上(n>>k)，寻求原始高维数据特征的线性组合，从而获得高维数据的有效低维表示[7-9]。然而，因为由PCA得到的数据的新特征是数据原特征的线性组合形式，往往缺乏可解释性。随后，Zou等[10]提出了稀疏主成分分析算法(Sparse Principal Component Analysis，SPCA)，将PCA表述为一个回归型的优化问题，并引入稀疏正则化项，从而将PCA转变为一种特征选择方法。SPCA不仅可以用于常规数据分析，还可以被有效地应用于基因表达阵列分析。但是，该算法是非凸的，难以得到全局最优解，当局部最优解不为全局最优时，性能很可能会发生非常显著的变化。Chang等[11]提出的凸稀疏主成分分析(Convex Sparse Principal Component Analysis，CSPCA)通过在SPCA中引入低秩惩罚项，并用l2,1-范数取代SPCA损失函数中的F-范数，得到了一种新的SPCA算法。CSPCA是一种全局最优的算法，在大量数据集上的实验结果表明，CSPCA具有优良的特征选择性能和对噪声的鲁棒性[12]。但是，CSPCA存在的问题是算法求解涉及矩阵求逆运算，当数据维数较高时计算复杂度较高，运行时间长，限制了CSPCA的应用范围。

针对CSPCA存在的上述问题，拟提出一种改进SPCA(Improved Sparse Principal Component Analysis,ISPCA)算法。该算法首先分别由第一阶段不加低秩惩罚项的SPCA和第二阶段执行带低秩惩罚项的SPCA依次对数据进行降维处理，然后在第一阶段利用矩阵的广义逆引理降低算法复杂度，从而提高整个算法的运算效率。

1 预备知识

为了方便表述，下面介绍使用的符号和规范定义，以及简要回顾经典主成分分析[13]、稀疏主成分分析[14]和凸稀疏主成分分析[15]的主要相关工作。

1.1 符号定义

设X=[x1,x2,…,xn]∈d×n为原数据矩阵，xi∈n(1≤i≤n)是第i个数据，d为行数，n为样本总数，XT表示X转置。W表示X的回归投影矩阵，对于矩阵W∈m×n，wi和wj分别代表W的第i行和第j列元素矩阵。Tr(W)表示矩阵W的迹，W的核范数被定义为

(1)

W的F-范数被定义为

(2)

W的l2,1-范数被定义为

(3)

1.2 主成分分析

PCA是一种数据降维的统计方法,旨在寻求原始高维数据变量的线性组合，从而获得高维数据的低维表示。PCA可以描述为一个回归型优化模型[16]，即

(4)

式中，r为矩阵W的秩，r(W)=k即矩阵W的秩数为k。

PCA是用最小二乘法求解，对噪声极其敏感。当数据含有噪声时，PCA投影方向偏离所期望的最优解。此外，PCA降低数据维数的同时，特征可能会发生变化，因此，其不能用于特征选择。

1.3 稀疏主成分分析

矩阵的l2,1-范数被证明能够使矩阵组稀疏化。因此，SPCA可描述为如下优化模型[16]

(5)

式中，α为非负正则化参数。

1.4 凸稀疏主成分分析

(6)

式中，β为W核范数的正则化参数。

2 改进的稀疏主成分分析算法

鉴于造成CSPCA计算复杂度高的原因主要是原子范数惩罚项的优化计算，因此ISPCA算法分为两阶段：第一阶段只用鲁棒的SPCA对数据进行无监督特征选择，以降低数据的维数，采用矩阵的广义逆引理降低运算复杂度；第二阶段对降维数据采用完整的CSPCA再进行一次特征选择，从而最终实现对原数据的特征选择。

ISPCA算法第一阶段可以描述为如下的最小化问题

(7)

式中：W′∈d×d为第一阶段权重矩阵，w′i表示W′的第i行，λ为的参数。因为该目标函数是凸的，所以利用式(7)对W′求导并令导数等于零，可得

(8)

令

(9)

(10)

考虑到D1∈n×n和D2∈d×d均为对角矩阵,因此式(8)的矩阵形式可表示为

XD1XTW′+λD2W′=XD1XT

(11)

简化式(11)可得唯一的最优W′为

W′=(XD1XT+λD2)-1(XD1XT)

(12)

直接计算(XD1XT+λD2)-1复杂度高，为O(d3)，因此为了提高计算效率，利用矩阵的广义逆引理对其求解。

定理若矩阵A∈n×n为非奇异矩阵，B∈n×p，C∈p×n，则有[18]

(A+BC)-1=
A-1-A-1B(I+CA-1B)-1CA-1

(13)

根据式(13)，令A=λD2，B=XD1，C=XT，可得出W′新的求解形式为

W′=(λD2)-1-(λD2)-1XD1·
[I+XT(λD2)-1XD1]XT(λD2)-1

(14)

式(14)求解W′的矩阵规模小于式(12)，因此将式(14)所求的W′对原数据进行一次特征选择，得到新的降维数据Y。

在ISPCA算法第二阶段，采用CSPCA算法，利用式(6)对第一阶段得到的降维数据Y再进行一次特征选择，得到最终特征选择后的数据Z。

ISPCA算法具体实现步骤如下。

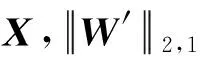
输出权重矩阵W′，第二阶段特征选择后的数据Z。

步骤1随机初始化第一阶段权重矩阵W′∈d×d。

步骤2利用式(9)和式(10)分别计算对角矩阵D1和D2。

步骤3将所求D1和D2代入式(14)求W′，得到第一次降维后的数据矩阵Y。

步骤4将数据Y代入式(6)，利用CSPCA再进行一次特征选择，得到最终特征选择后的数据Z。

3 实验结果与分析

3.1 实验设置

选取人类肺癌[19](the human lung carcinomas,LUNG)、恶性神经胶质瘤[19](the malignant glioma，GLIOMA)、ALL/AML白血病数据[19](ALL/AML Leukemia，ALLAML)、结肠肿瘤[19](Colon Tumor，COLON)和前列腺癌基因表达[19-20](Prostate Cancer gene expression，PRO-GE) 等5个均为维度高的基因表达数据集，在Intel Core i5-1135G7 2.4 GHz CPU 16 GB中Windows 10操作系统上，利用仿真工具Matlab 2017b完成实验。各数据集的相关特性如表1所示。

表1 5个数据集的相关特性

3.2 收敛性分析

ISPCA算法的两阶段目标函数均单调递减，在第一阶段是凸优化问题，因此对第二阶段的收敛性进行分析。考虑到正则化参数调整范围的中值为1，将α和β设定为1，不同数据集下ISPCA算法的目标函数值的收敛分析曲线如图1所示。由图1可以看出，ISPCA算法的目标函数值随迭代次数是单调递减的，并且在所有数据集上均能在15次迭代内快速收敛。

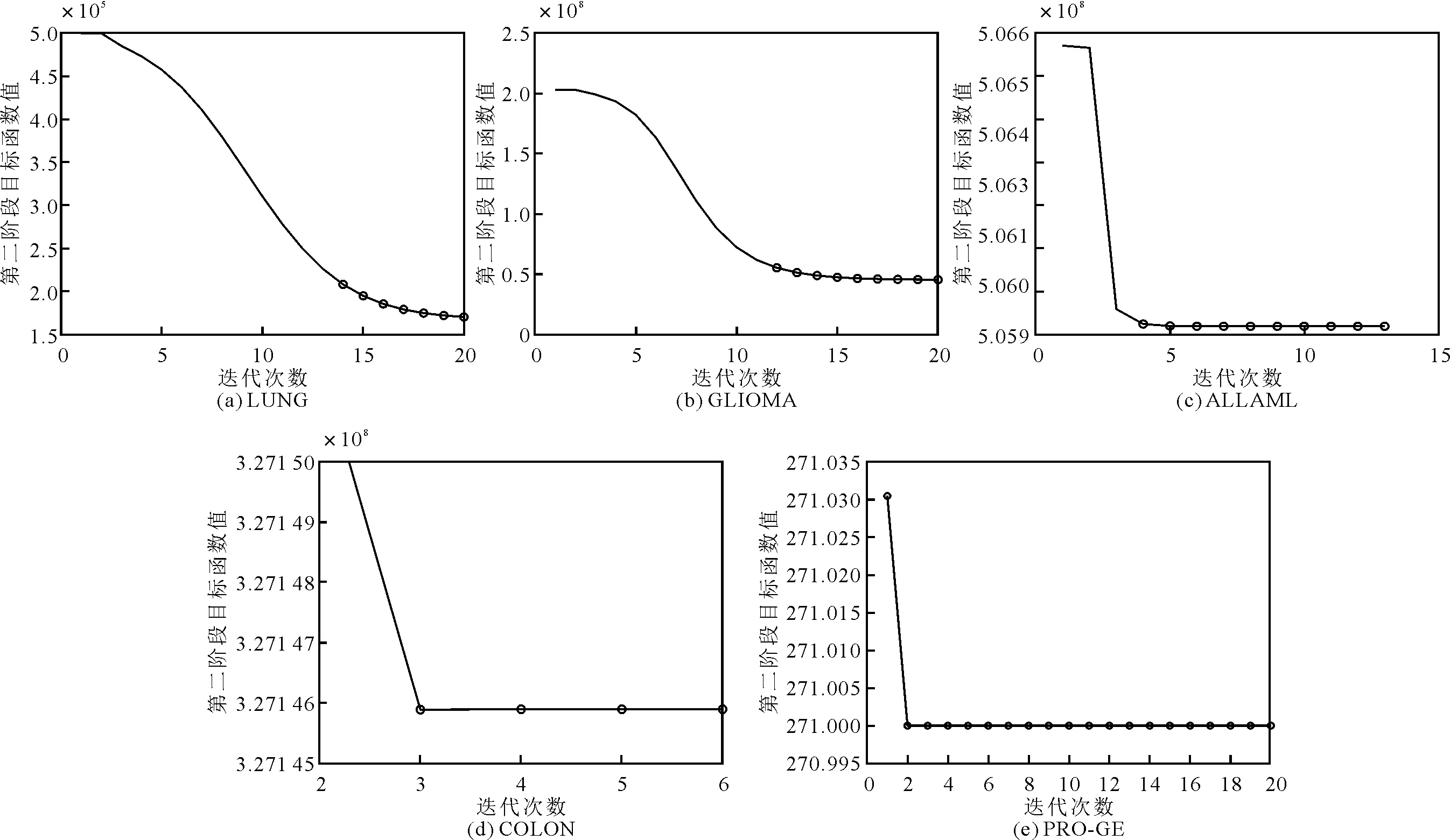
图1 收敛性曲线

3.3 聚类精度分析

ISPCA是无监督特征选择算法，为了验证ISPCA算法的有效性，分别将ISPCA算法与CSPCA、无监督判别特征选择[21](Unsupervised Discriminative Feature Selection，UDFS)、多集群特征选择[22](Multi-Cluster Feature Selection，MCFS)、高斯拉普拉斯算法[22](Laplacian of Gaussian Algorithm，LGA)和具有多子空间随机化和协作的无监督特征选择[23](Unsupervised Feature Selection with Multi-Subspace Randomization and Collaboration，SRCFS)等无监督特征选择算法进行对比。利用K-means聚类算法对特征选择后得到的数据进行聚类，将聚类精度作为特征选择算法性能评价的指标。实验中对每组数据设置随机重复聚类30次，并选其最佳聚类精度作为最终聚类精度。

实验中所有算法参数都将在集合{10-6,10-4,10-2,1,102,104,106}中选择，分别对表1中的数据集进行20%和40%的特征选择。当选择20%特征时，6种算法在5个数据集上的最优聚类精度如表2所示。ISPCA算法在第一阶段选择80%，第二阶段选择25%的特征，保证最终选择的特征范围为20%。

表2 特征选取20%时6种算法的最优聚类精度/%

当选择40%特征时，6种算法在5个数据集上的最优聚类精度对比如表3所示。ISPCA算法在第一阶段选择80%，第二阶段选择50%特征,保证最终选择特征为40%。

表3 特征选取40%时6种算法的最优聚类精度/%

由表2及表3可知，当特征选择范围为20%和40%时，ISPCA相较于CSPCA算法，聚类精度都有不同程度提升，并且在6种算法中聚类精度结果最优。

3.4 运算效率分析

当数据特征分别选取20%和40%时，6个算法在最优精度下的运行时间分别如表4和表5所示。

表4 特征选取20%时6种算法最优精度对应的运行时间/s

表5 特征选取40%时6种算法最优精度对应的运行时间/s

由表4和表5可知，特征选择范围为20%和40%时，ISPCA算法相较于CSPCA算法而言，总体计算运行时间减少，并且当特征选择范围为40%时，ISPCA的运行时间整体少于UDFS及MCFS算法。在特征选择范围为20%时，ISPCA在COLON和PRO-GE数据集的运行时间少于UDFS及MCFS算法，即ISPCA的运行复杂度低于UDFS及MCFS算法。

4 结语

将改进的稀疏主成分分析法ISPCA应用于无监督特征选择中，分别在第一阶段引入矩阵广义逆引理和第二阶段采用低秩惩罚项的稀疏主成分分析对数据进行降维处理，从而降低算法的复杂度。在5个真实数据集上的对比性实验结果表明，ISPCA算法不仅在聚类精度优于CSPCA算法，而且在运行速度上表现更优。