仿生非光滑摩擦衬片对制动器摩擦振动的影响
王国明,袁 琼
(重庆工业职业技术学院,重庆 401120)
0 引言
车辆盘式制动器是利用制动盘和摩擦衬片相互摩擦产生制动力矩,将汽车的动能转化为摩擦功,以达到减速乃至停车的目的,因此,制动器是保证车辆安全运行的重要装置[1]。如今,制动器在摩擦运动过程中产生的振动噪声问题严重,影响了车辆品牌价值和乘客舒适体验,成为人们长期关注的热点问题[2]。
鉴于制动摩擦副界面是摩擦振动产生的关键区,目前对制动界面特征和摩擦振动之间关系开展大量研究,并认为合理的摩擦表面形貌对降低制动摩擦振动产生积极的影响[3]。近年来,随着仿生学和摩擦学的发展,仿生设计已被广泛应用在许多研究领域[4-7]。研究发现,许多生存在恶劣环境下的生物体表面具有不同的非光滑形态,如凹坑、鳞片、凸包等。这些非光滑表面形态具有优良的摩擦学特性,能有效改善接触界面摩擦学行为[8]。因此将仿生非光滑表面技术应用到制动摩擦副上,能为改善制动摩擦振动噪声问题提供新途径。
目前,研究者已对仿生设计和车辆制动行为之间的关系展开研究。Wang等[9]通过对蝗虫表面以及牙齿表面等的形貌分析,设计出具有类似表面特征的非光滑汽车制动盘,结合数值计算与试验研究,验证了该类制动盘具有很好的制动性和耐磨性。黄晓华等[10]设计出3种带有仿生散热筋的制动盘,并对其散热性能进行分析研究,为仿生散热筋在高速列车制动盘的应用提供了参考依据。杨肖等[11]对3种不同的仿生制动盘的表面温度场与应力场进行模拟,发现仿生制动盘能够降低制动盘表面的温度梯度和应力,从而改善盘面热疲劳问题。
以上研究主要针对仿生制动器的磨损与热行为进行探讨,而利用仿生设计来实现制动器的减振降噪的报道相对较少。Hammerström等[12]在汽车制动盘表面加工出螺旋状喷砂图案,制动试验结果表明汽车的制动噪声强度产生明显下降,但降噪效果与喷砂图案的磨损程度关系密切。Nouby等[13]在摩擦衬片表面加工出特定尺寸和排布的沟槽,降低了制动振动噪声强度,但该工作并未引入仿生设计的概念,不具有仿生设计的代表性。同时,关于这类沟槽对制动振动噪声影响的机理也没有得到系统的解释,因此关于表面仿生设计和制动振动噪声之间的关系没有得到很好的说明,无法为改善制动摩擦振动噪声的制动盘/摩擦衬片表面仿生设计提供参考。
为此,本研究设计出3种具有非光滑仿生表面的摩擦衬片,即表面圆坑片、表面方坑片和表面混合片(方坑与圆坑交错排列)。采用有限元分析对仿生摩擦衬片和光滑摩擦衬片的摩擦振动特性进行对比,理论验证仿生摩擦衬片对制动摩擦振动行为的影响,揭示其作用机理,为改善制动摩擦振动的摩擦衬片表面仿生设计提供依据。
1 盘式制动器和非光滑仿生表面摩擦衬片
1.1 盘式制动器模型
在三维建模软件中,对某型汽车盘式制动器三维模型进行参数标定,并导入ABAQUS中划分网格,得到制动器有限元模型如图1(a)所示。该制动器主要由制动盘、摩擦背板、摩擦衬片、制动卡钳、保持架和液压缸组成,制动摩擦衬片即由摩擦衬片和及其背板组合而成。对于制动盘、背板和摩擦衬片等相对规则的部件,通过定义全局网格种子数目,采用Sweep(扫掠)方式直接对它们划分网格[5]。对于保持架和制动卡钳两个不规则的部件,采用4面体单元(C3D4)划分网格,如图1(b)所示。制动器模型总单元数为362 587个。模型各部件的材料参数和网格特性列于表1。

图1 盘式制动器及其部件有限元模型Fig.1 Finite element model of disc brake and its components
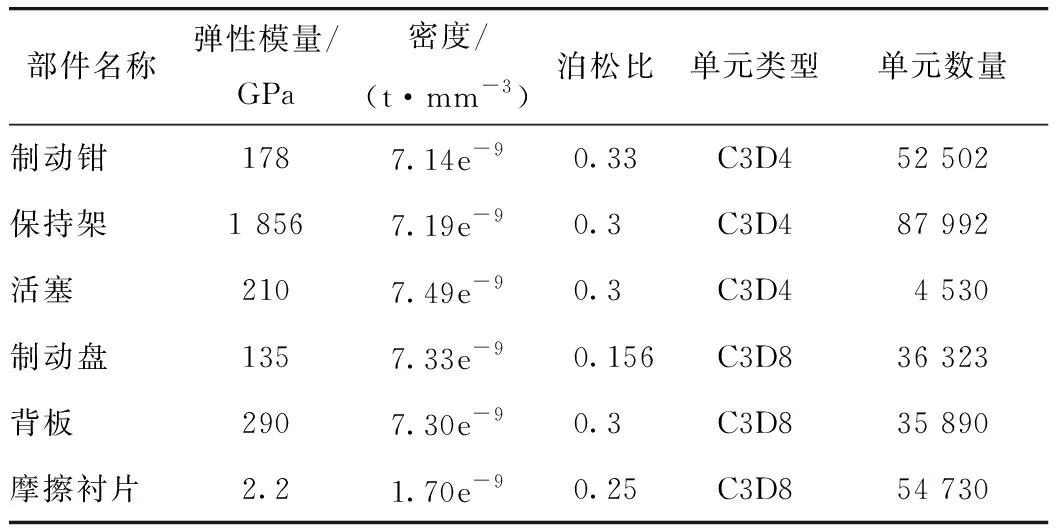
表1 盘式制动器各部件材料参数Tab.1 Material parameters of disc brake components
1.2 模型接触关系与边界条件
参照文献[14],盘式制动器各部件之间的连接关系如表2所列。参照文献[15-16],发现在摩擦衬片与制动盘之间的试验摩擦系数通常存在的范围是0.2~0.7之间。且在关于制动器摩擦振动问题的数值模拟研究中,研究者一般采用的摩擦系数均在此范围之内[17],因此本研究定义制动盘和摩擦衬片之间的摩擦系数范围为0.3~0.6。对于其他摩擦副区域,由于发生相对运动位移幅值较低,因此在计算分析中定义为较低的摩擦系数值(0.1)[5]。

表2 各部件之间的连接关系Tab.2 Connections between components
1.3 3种非光滑仿生表面制动盘设计
随着仿生学领域探讨的不断深入,研究结果表明生物非光滑体表耐磨特性更好。生物表面的形貌特征也各有差异。这类非光滑体表包括凸包、条纹、凹坑、网格状等多种形态。研究表明这种非光滑表面对抵抗外界环境的摩擦磨损起到了极其重要的作用[8]。
通过对蝗虫腿部和牙齿表面进行SEM(扫描电子显微镜)观察后发现,它们的表面均呈现出明显的非光滑特性。以牙齿为例,其牙齿咀嚼面呈现出与进食方向平行的条纹结构。 这有利于对实物进行充分的粉碎和咀嚼,同时降低砂粒对牙齿表面的磨损[15]。综合而言,蝗虫的腿部和牙齿等在与外界环境产生频繁摩擦,呈现出凹坑、凸起、条纹等不规则结构,可减少表面磨损,从而提高界面的摩擦学性能。
相类似的是,制动器通过制动盘和摩擦衬片直接的相互接触摩擦,实现车辆的减速乃至停止。在摩擦过程中,接触界面由于温升持续且磨屑、砂砾等存在,使接触摩擦行为复杂,摩擦磨损程度严重。基于这些非光滑表面具有改善摩擦磨损方面的特性,且考虑到摩擦衬片的表面较为光滑,根据相似性原理,本研究选取了具有代表性的且比较规则的圆坑、方坑和混合坑3种表面结构进行加工。
通过调研大量的与蝗虫有关的仿生模拟研究相关工作,发现相似系数的选择范围通常在10 000∶1至200 000∶1之间,同时为了保证合理的制动接触面积以及易于加工的原则,本研究选择30 000∶1的相似系数进行模拟分析。考虑到蝗虫表面凹坑直径约为100 nm[18-19],因此在摩擦衬片仿生表面构建中按 1∶300 00的比例进行设计,即在摩擦衬片表面加工出的圆坑直径为3 mm。考虑到蝗虫表面凹坑深度为30 nm,因此将对应圆坑/方坑的深度均取为0.9 mm。为确保每个摩擦衬片所加工出来的仿生表面面积相等,对方坑的尺寸做了适当修改, 即取方坑边长为3.544 mm。定义每列圆/方坑中心距为6 mm。非光滑仿生摩擦衬片的表面结构如图2所示。
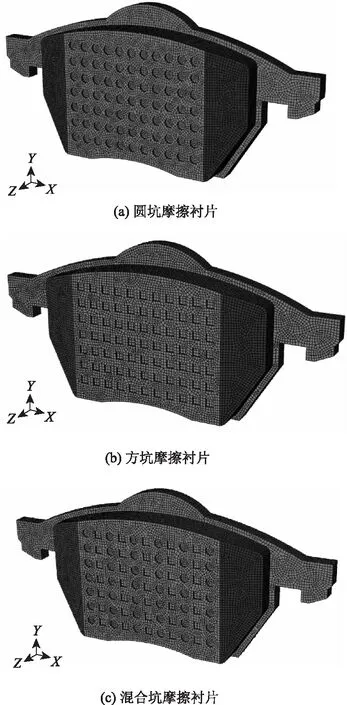
图2 3种非光滑仿生表面制动摩擦衬片Fig.2 Friction linings with 3 kinds of non-smooth bionic surface
2 非光滑仿生摩擦衬片模态特性分析
2.1 自然频率分析
首先计算在自由状态下,盘式制动器各个部件在特定范围内的自然频率分布特性。通过描绘出各部件每一阶自然频率的分布情况,预测制动器各个部件之间可能接近的频率,结果如图3(a)所示。在0~12 000 Hz的频率范围内,制动盘、制动钳和摩擦衬片的自然频率分布较宽,出现的模态阶次相对较多。尤其是制动盘,在该频率范围内出现的模态数量为55。因此当制动器产生高频振动或者低频颤振时,制动盘均有可能存在特定的振动模态。对各个部件频率分布较为集中的区域进行分析,可知在频率约为2 200,3 300,6 000,8 000 和11 000 Hz左右的区域,各部件间存在自然频率非常接近的情况。可以推测,在摩擦力的作用下,不同部件之间可能存在模态频率相接近现象,从而形成部件之间的耦合运动,并在上述频率附近产生摩擦振动和噪声。
进一步地,观察3种非光滑仿生摩擦衬片的频率分布特性,对仿生摩擦衬片和系统振动特性之间的关系进行预测,结果见图3(b)。非光滑仿生摩擦衬片同阶次的自然频率低于光滑摩擦衬片。这是由于仿生摩擦衬片的表面处理引起摩擦衬片结构发生变化,制动器整体刚度降低,因此自然频率的分布密度上升,而自然频率的数值减小。可以推测,摩擦衬片结构变化导致自然频率发生改变,从而影响制动器的耦合频率,因此仿生摩擦衬片,可以改变制动器振动性能的稳定性。

图3 制动器各零部件和仿生摩擦衬片自然频率分布Fig.3 Natural frequency distributions of brake components and bionic friction linings
2.2 模态振型分析
进一步地,不同摩擦衬片在0 ~12 000 Hz的频率范围内的自由模态的分析,结果见图4和表3。光滑摩擦衬片和仿生摩擦衬片的自由模态特性与频率值均很接近。这是由于制动摩擦衬片背板弹性模量远大于摩擦衬片材料,因此削弱了摩擦衬片表面处理对制动摩擦衬片模态的影响。但是,由于摩擦衬片的表面处理方式不同,依然会导致制动摩擦衬片的局部模态发生变化。如在第2阶模态中,方坑摩擦衬片与混合摩擦衬片在该阶模态较为接近,但与光滑摩擦衬片和圆坑摩擦衬片的模态差异显著。此外,仿生摩擦衬片在高频频段的局部模态振型更明显,表面圆坑与方坑区均出现一定程度的变形。

图4 光滑摩擦衬片和仿生摩擦衬片的各阶自由模态对比Fig.4 Comparison of free modes of each order between smooth friction lining and bionic friction lining

表3 不同摩擦衬片的自然频率特性Tab.3 Natural frequency characteristics of different friction linings
3 非光滑仿生表面摩擦衬片对制动振动性能稳定性影响的分析
3.1 制动稳定性评价指标
在制动器摩擦振动噪声的预测分析中,复特征值分析法最为常见[5, 20]。利用ABAQUS进行制动器的复特征值求解,建立制动器动力学方程:
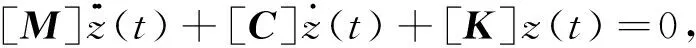
(1)
式中,M为系统质量矩阵;C为阻尼矩阵;K为刚度矩阵。刚度矩阵K因为存在摩擦项而变为不对称矩阵,因此制动器的振动响应z(t)的通解可表示为:
(2)
式中,j为系统对应的模态阶次;{φ}为系统第j阶模态的模态向量;Sj为系统的特征值。Sj表达式为:
Sj=Aj+iBj。
(3)
由式(3)可知,当特征值实部Aj>0时,振动响应z(t)的值随时间增大而逐渐增大。这说明制动器系统产生自激振动,此时所对应的虚部值Bj即为制动器系统产生摩擦振动的频率。利用特征值实部和虚部构造新的参数:负阻尼比ξj。
其表达形式为:
ξj=-Aj/(π|Bj|),
(4)
制动振动具有多频成分,通常采用倾向性系数(Tendency of Instability)作为制动振动倾向和强度的评价指标[5, 21],其计算式为:
(5)
式中TOI为振动倾向性系数。
当它的值越大时,制动器产生振动与噪声的趋势和强度越大。这也成为在多频振动状态下,制动器振动性能稳定性强弱的主要判断依据[5]。
3.2 制动器系统稳定性分析
对不同制动器(光滑摩擦衬片/仿生摩擦衬片)在制动过程中产生的复特征值进行求解,结果如图5所示。当摩擦系数为0.6时,光滑摩擦衬片和圆坑摩擦衬片所对应的制动器系统均出现了12个不稳定振动频率,相比之下,方坑摩擦衬片和混合摩擦衬片所对应的制动器系统出现不稳定振动频率的数量明显降低,均为9个。进一步分析可知,在摩擦衬片表面加工出仿生非光滑表面结构时,制动器系统不会产生频率为2 337 Hz的振动,即制动器系统出现低频振动的数量减少。但是,由于表面仿生结构的存在,会导致制动器系统产生频率为7 220 Hz左右的摩擦振动,即制动器系统出现高频振动的数量增多。产生上述现象的原因是由于摩擦衬片表面进行处理后,它的结构和自然频率发生变化,导致它在其他阶次的频率与制动器其他部件在特定阶次的自然频率非常接近,因此与制动器其他部件发生耦合的阶次发生改变,从而导致制动器系统产生的振动频率也发生变化。
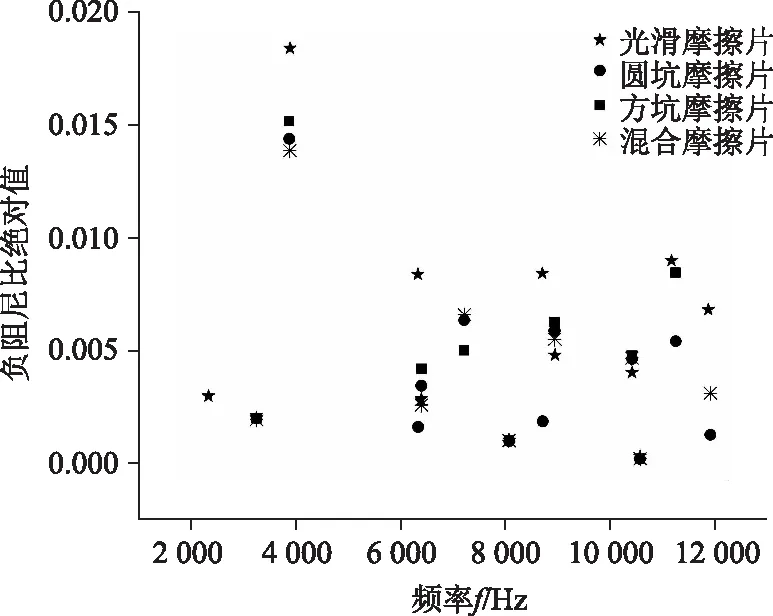
图5 不同摩擦衬片状态下制动系统的负阻尼比分布情况Fig.5 Distributions of negative damping ratios of brake system with different friction linings

图6 不同摩擦衬片状态下不同制动系统的振动模态Fig.6 Vibration modes of different brake systems with different friction linings
如图6所列,在不同摩擦衬片状态下,不同制动器系统可能出现的振动模态。由于制动盘为板式结构,且频率分布范围较广,因此制动器系统绝大部分的模态主要表现为制动盘的轴向与周向变形。但由于摩擦衬片经过表面处理后,部分与制动摩擦衬片有关的局部模态发生明显变化,如在振动频率为3 880 Hz附近,由于摩擦衬片结构变化导致局部振型差异显著,不同制动器系统的制动钳钳指的变形特性明显不同;当制动器系统在频率为7 220 Hz附近振动时,制动摩擦衬片的局部振动即为制动器系统的主要振动模态,即摩擦衬片进行表面处理后,其与制动器其他部件发生耦合的阶次产生变化,因此出现了新的振动模态。
进一步地,对该摩擦系数下不同制动器系统的TOI值进行计算,结果见表4。对于光滑摩擦衬片,其对应制动器系统的TOI值为216.401;当在摩擦衬片表面加工出圆坑时,其对应制动器系统的TOI值为150.105;对于方坑摩擦衬片,其对应制动器系统的TOI值为147.36;相比之下,当在摩擦衬片表面加工出混合坑后,其对应制动器系统的TOI值明显下降,仅为123.609。综上分析可知,在摩擦衬片表面加工出仿生表面后,制动器系统产生不稳定振动特性的倾向明显下降,尤其当摩擦衬片表面加工出方坑或混合坑后,制动器产生不稳定振动频率的数量明显下降,且具有混合坑表面的摩擦衬片在降低制动器系统振动强度方面的效果最佳。
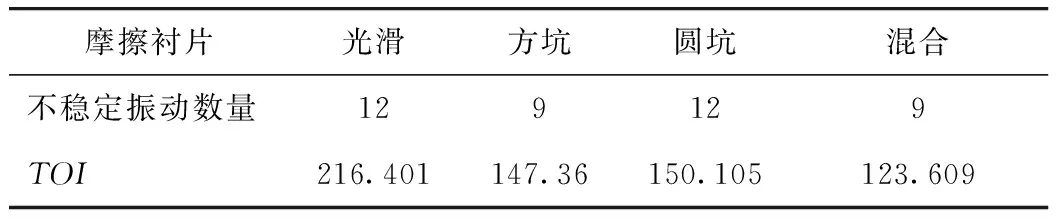
表4 不同摩擦衬片状态下制动器不稳定振动数量和TOITab.4 Unsteady vibrations and TOIs of brake with different friction linings
3.3 TOI演变特性分析
考虑到制动摩擦振动的产生是一个从无到有的演变过程,且在不同摩擦系数状态下,制动器系统出现的耦合频率和振动特性可能有所区别,见图7。
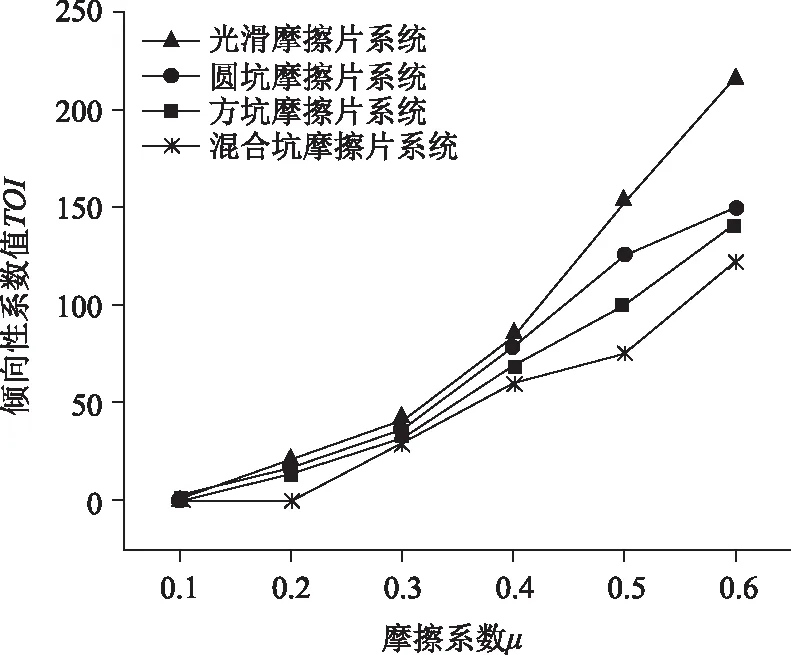
图7 不同制动器的TOI值随摩擦系数的变化曲线Fig.7 Curves of TOIs of different brake systems varying with friction coefficient
随着摩擦系数增大,制动器系统的振动倾向均逐渐增大。这是由于摩擦系数的增大导致制动器系统发生模态耦合的数量增多,因此可能出现的振动倾向和强度逐渐变大[22]。虽然仿生摩擦衬片对应的制动器系统的TOI值也趋于增大,但是其整体幅值均小于具有光滑摩擦衬片的制动器系统,该分析结果进一步说明了通过对摩擦衬片进行仿生表面处理,能够降低系统振动倾向,改善制动器系统摩擦振动稳定性。尤其是在摩擦衬片表面具有混合坑结构形态后,其所对应的制动器的TOI值最低,因此制动器系统的摩擦振动稳定性最强。
3.4 接触状态分析
为了解释仿生摩擦衬片在改善制动器系统振动噪声的机理,同时考虑到制动振动的产生源于摩擦界面的不稳定振动,本节对不同制动器的液压缸侧的接触应力进行分析,结果如图8所示。当摩擦衬片表面仿生处理后,制动盘摩擦表面应力分布情况发生改变,界面应力分布区域明显增大,且表面应力幅值有一定程度的下降。这表明摩擦衬片表面处理后,改善了应力集中现象,使应力分布更加均匀,从而削弱了能量堆积趋势,改善了制动器的振动摩擦振动特性的稳定性[5, 23]。此外,在摩擦衬片表面加工出混合坑后,摩擦界面的应力幅值最小,应力梯度较均匀,因此其所对应的制动器摩擦振动特性的稳定性最好,出现的振动倾向也最弱。以上分析结果与图8所示的TOI分析结果相一致。

图8 不同摩擦衬片的制动盘接触应力Fig. 8 Contact stresses of brake discs with different friction linings
在常见的制动器摩擦副接触应力分析中,摩擦衬片的应力通常集中在摩擦衬片的前边缘区。在摩擦衬片表面仿生处理后,由于接触应力值减弱,所以应力分布更均匀,但最大应力依然出现在摩擦衬片的前边缘区。这也与应力集中现象的一般规律相符合。
4 结论与展望
本研究设计出3种具有非光滑仿生表面的摩擦衬片:圆坑、方坑和混合坑摩擦衬片,利用ABAQUS对3种非光滑仿生表面摩擦衬片进行了制动摩擦振动性能的分析,并与具有光滑摩擦衬片的制动器进行对比。主要结论如下:
(1)摩擦衬片表面经仿生处理后,摩擦衬片表面结构形态发生了改变,整体刚度降低,自然频率值减小。摩擦衬片自然频率的改变将对制动器的耦合频率产生影响。
(2)摩擦衬片表面仿生处理后,制动器发生模态耦合频率和耦合数量均发生变化,出现了部分振动频率消失和新增的现象。这表明仿生摩擦衬片与制动器其他部件发生耦合的阶次发生了改变,使制动器工作产生的振动频率也发生变化。
(3)摩擦衬片表面非光滑仿生处理后,制动器的摩擦振动倾向和强度明显减弱。在3种非光滑仿生摩擦衬片中,混合坑摩擦衬片在改善制动器制动摩擦振动性能的稳定性上效果最佳,其对应的TOI值最小;而圆坑摩擦衬片在3者之中抑制制动振动的效果最弱。
(4)摩擦衬片表面的仿生设计与处理,改善了制动界面应力集中现象,使应力分布更均匀,从而削弱了界面能量堆积现象,改善了制动器摩擦振动性能的稳定性。尤其混合坑摩擦衬片表面加工后,摩擦界面应力幅值最小,应力梯度较为均匀,因此其所对应的制动器振动性能的稳定性最好。
在后续工作中,将搭建制动器台架试验系统,对具有不同仿生表面的摩擦衬片进行制动试验;将对试验与数值模拟结果进行对比分析,从而进一步验证仿生摩擦衬片在改善制动振动噪声方面的可行性。同时,将设置各个结构(圆坑/方坑)的尺寸、排布等作为影响因子参数,采用试验设计(DOE)结合响应曲面法,对各影响因子的显著性进行分析,并得到降低制动摩擦振动噪声的最优解决方案。

