大型原油储罐的罐体变形测量及计算方法研究

许皆乐 周忠贺 王亚东

（1.浙江省特种设备科学研究院；2.浙江省特种设备安全检测技术研究重点实验室）

大型原油储罐是国家原油储备和输转的重要设备，一旦发生安全事故后果严重。 因此，储罐尤其100 000 m3以上的大型原油储罐的安全服役对整个石油储运业至关重要。 而影响储罐安全性的各种因素中，罐体变形是最为重要的，也是评价储罐安全性的关键指标［1］。

常规服役储罐的罐体变形通常由不均匀的基础沉降、运行时罐壁所受的应力作用等原因引起。 罐体变形可能引起浮盘卡住或密封失效继而造成原油的挥发损耗、污染环境等危害。 在储罐检修期间，测量罐体的变形应作为停工检测中的一项主要内容，其中最关键的两个测量项目就是椭圆度和垂直度［2］。 笔者采用高精度全站仪对某台100 000 m3的原油储罐实施测点坐标数据的采集，并算得椭圆度和垂直度，以判断该罐体的变形状况。

1 常见测量方法

椭圆度的定义是指圆形横截面上最大直径和最小直径的差。 因此，这基本上属于直径法，凡是能测量直径的方法都可以用来测量椭圆度。 对于小型的容器、管材和棒材，可以采用特定的直径测量仪或测量尺进行测量，但对直径80 m以上的大型原油储罐来说，显然不适用，工作人员需采用合适的仪器测量。

垂直度的测量，最简单和常见的方法是采用吊线法，但这种方法的测量精度受天气、人为操作等因素的影响较大，且工作效率不高，还存在一定的安全隐患［3］。如果有一种方法能快速、精确地测出储罐罐体各个指定方位的垂直度，并且又能同时开展椭圆度的测量，便能使罐体变形的测量更为高效和可靠。

2 测量方法的确定

由于大型原油储罐在停工检修期间，外浮盘已落至罐底，因此罐体内大部分空间已外露。 选择采用高精度全站仪架设在浮盘上表面，利用其逐点逐圈测量的功能，从下往上依次测量罐内壁上的坐标值，测量的数据可同时用于椭圆度和垂直度的计算，全站仪测量示意图及其现场照片如图1所示。

图1 全站仪测量示意图及其现场照片

3 罐体变形的测量

3.1 测量工程概况

某国家石油储备基地一台容积为100 000 m3的原油储罐， 停工检修期间实施罐体变形测量。主要测量项目为罐体的椭圆度和垂直度。 经资料审查，该原油储罐的主要参数如下：

结构形式 双盘式外浮顶

内径 80 m

罐体高度 21.8 m

圈板层数 9层

每层圈板高度 2.4 m

3.2 现场数据采集

测量人员携带设备到达浮盘上表面，将全站仪通过三脚架牢固地架设在尽量靠近储罐圆心的位置。 开机后，调整全站仪对中整平［4］，开启激光束。 此时浮盘高度位于底部第2层圈板的中下部，该部位以上为测量区域，即设置底部第2层圈板的3/4高度为第1个测量圈， 以上每层圈板高的1/4和3/4处依次设置测量圈［5］，共计15 个（图2）。 通过每层圈板高度（2.4 m），可计算15个测量圈距离环焊缝的固定高度。

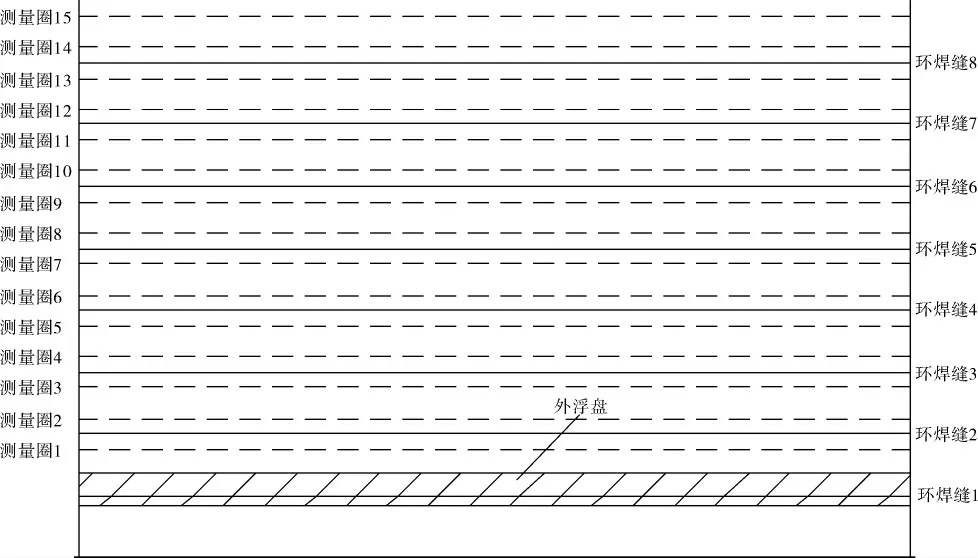
图2 各测量圈位置示意图

为保证所有测点不被量油管、导向管及旋转扶梯等附件挡住， 测量圈1圆周方向的起始位置可设置在离量油管不远的罐壁上（500 mm左右即可）。 由测量圈1的高度确定整体测量的起始位置，并在罐壁上做标记，调整全站仪焦距将激光束对准标记。 需要注意的是，每圈测点数太多会影响测量效率， 测点数太少又会影响测量精度，一般选取24个（可按实际选取，不绝对）均布的测点（图3）。

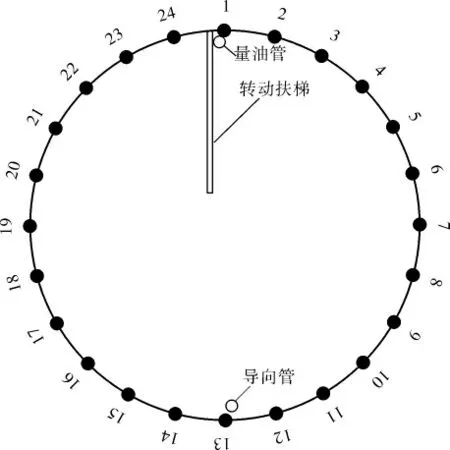
图3 每个测量圈上测点分布示意图

将上述确定好的圈板层数、每层圈板高度、测量圈距焊缝位置、每圈测点数、步进方式及起始位置等参数输入全站仪系统，开始逐层测量，仪器将记录每个测点的坐标数据（x，y，z）。

4 罐体椭圆度计算

4.1 整体思路

储罐的横截面并非绝对的圆，通过最小二乘法可寻求最佳的圆曲线，使拟合数据与实际数据间的误差平方和最小。 因此，先从每个测量圈的24个测点中任意选取23个点（共有24种取法），再通过最小二乘法拟合出24个圆曲线，选出直径的最大值和最小值即可。

4.2 计算过程

设每个测点的坐标为（xi，yi），i取1，2，3，…，N，则测点到圆心的距离di为：

对于测量圈1， 从24个测点中任意选取23个点（N=23）进行拟合计算，24种选法可得到24条圆曲线，其主要参数圆心（A，B）、半径R和直径Φ的计算结果见表1。

从表1中选出直径的最大值和最小值分别为80.014 3 m和80.009 4 m，两者相差4.9 mm，该差值即为测量圈1的椭圆度。

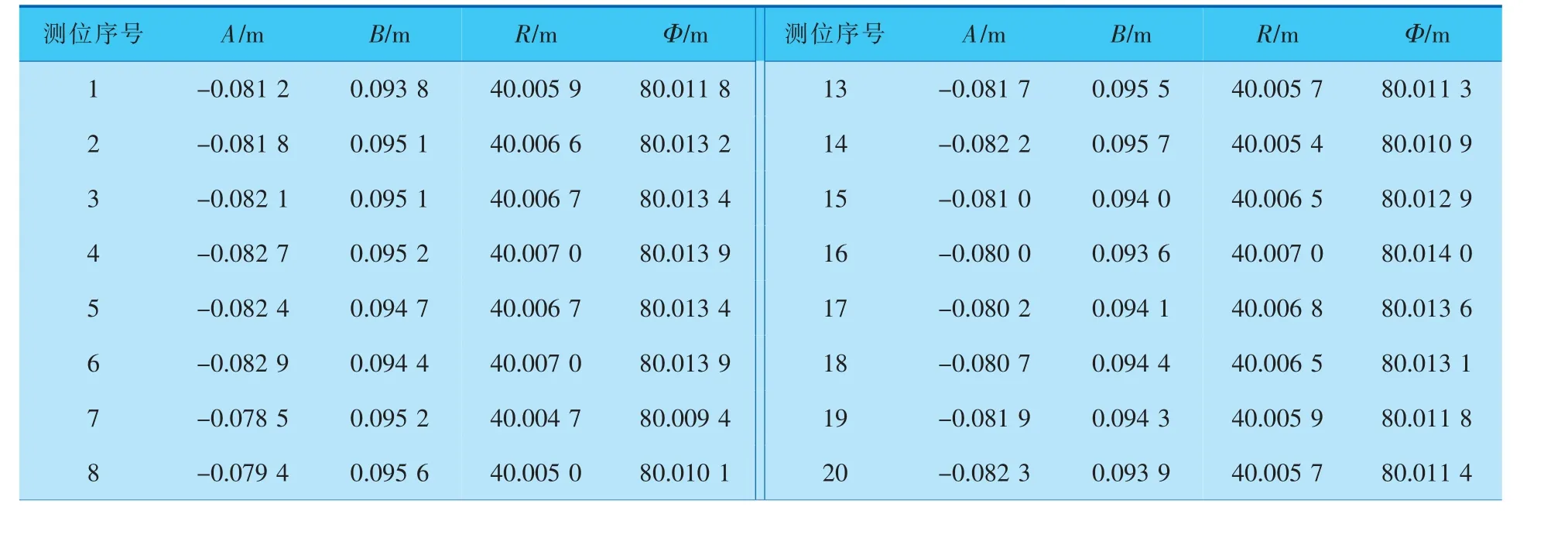
表1 测量圈1拟合24个圆的主要参数计算结果

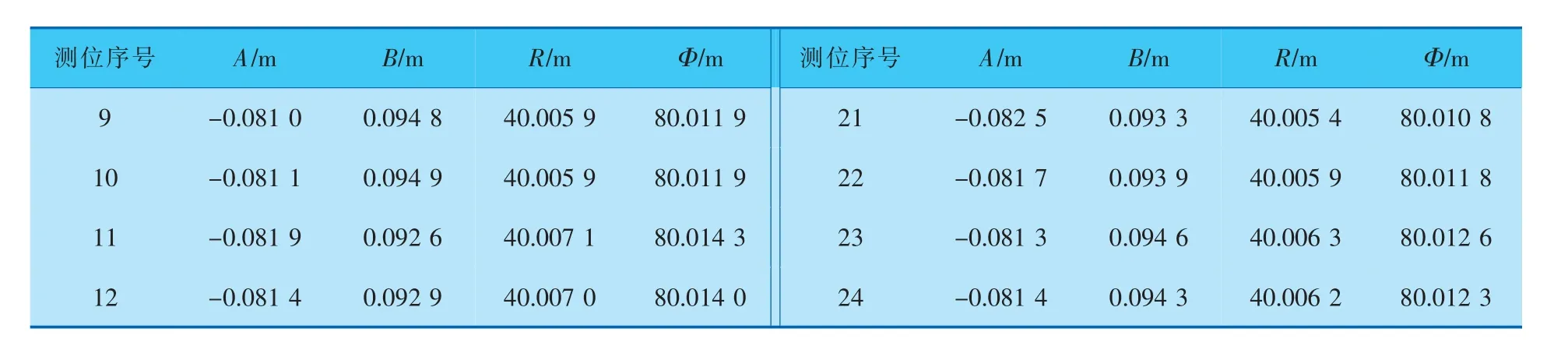
（续表1）

同样方法可计算出测量圈2～15的椭圆度，计算结果见表2。

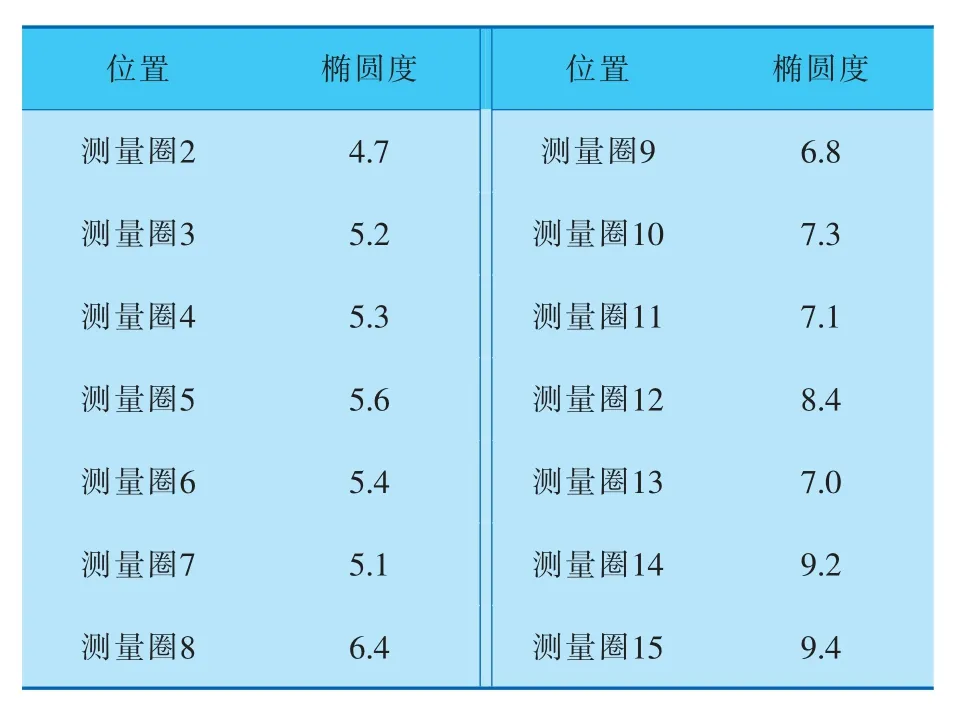
表2 测量圈2～15的椭圆度mm

5 罐体垂直度计算

5.1 整体思路

由某一测量圈上各测点的坐标值，通过最小二乘法拟合一条最佳直线，该直线的斜率通过换算即可得到此方位上的垂直度。 按同样的方法，可以求出所有24个方位上的垂直度。

5.2 计算过程

设定平面系中线性回归方程为Z=kL+b，某一测量方位上的测点与直线之间的竖直距离为li=Zi-（kLi+b），以此来表示两者之间的接近程度。 令函数M（k，b）为li的平方和，即：

对于图3中1号测位，沿罐壁从下往上共有15个测点（n=15），将各测点的L和Z值代入后，拟合出直线的斜率k=-87.4142、截距b=3516.5237（若斜率小于零且截距大于零，则说明该测量方位的罐壁内倾；反之，则说明罐壁外倾），线性回归方程为Z=-87.4142L+3516.5237。该斜率经三角函数换算，可得出1号测位的垂直度为1.144%。 同样，按此方法计算出其余23个测位的垂直度并断定测位处罐壁的倾斜方向，结果见表3。

表3 2～24号测位的垂直度及罐壁倾斜方向

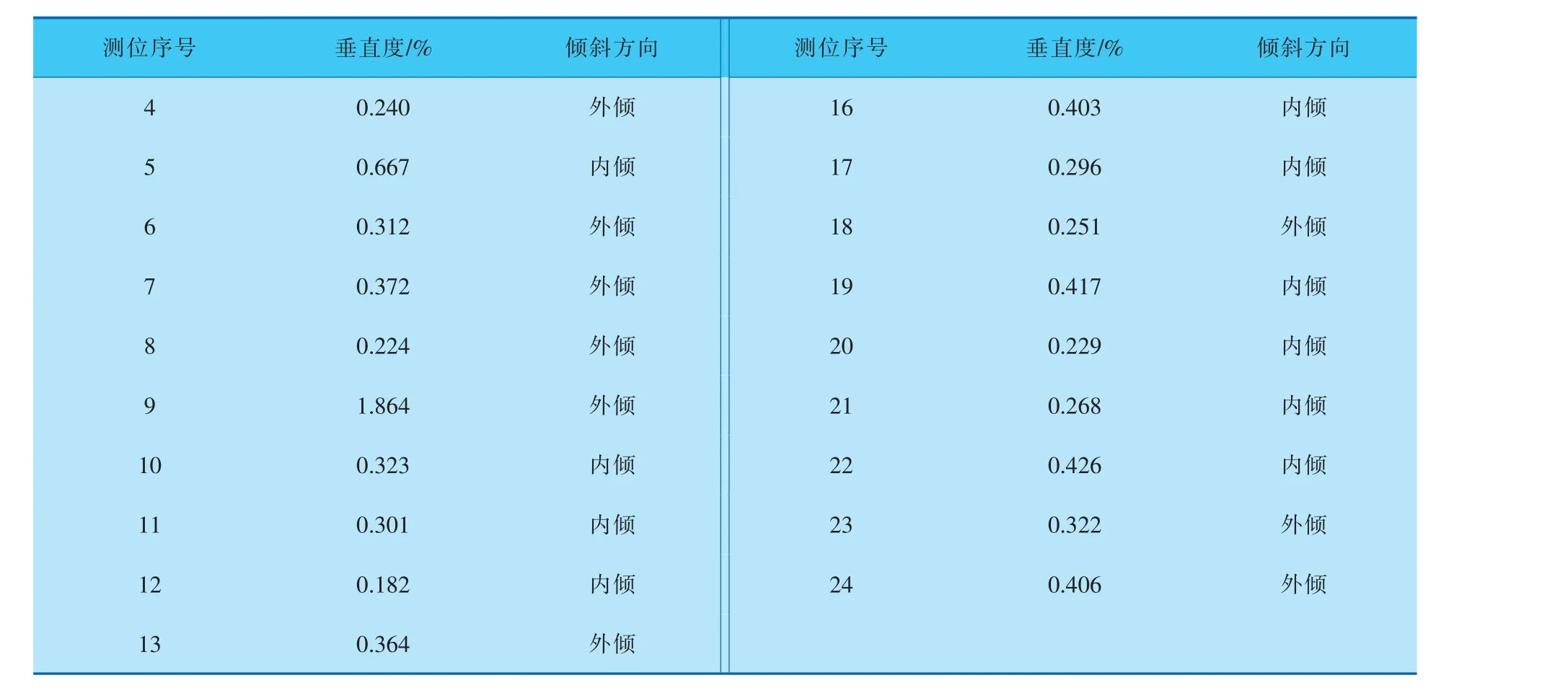
（续表3）

6 结束语

采用全站仪测量大型原油储罐的椭圆度和垂直度，计算所需的数据在完成一次自动测量后可同时获取，最大的优点在于大幅提高了测量效率和精度。 椭圆度和垂直度的计算均基于最小二乘法，前者是圆曲线的拟合，后者是线性拟合。 该方法计算过程虽较为繁琐，但模式固定。 在完成首台储罐测量计算的基础上，可通过编程来简化人工计算过程，后续任何立式圆筒形储罐在输入坐标数据后，均可利用该程序直接得出结果。

本次测量过程中选择了24个方位和15个测量圈用于方法的研究。 如现场条件允许，可增加方位和测量圈的数量， 测点之间则更为密集，可用于储罐已出现明显变形并需对变形位置进行定位和定量的场合，保证拟合结果与储罐实际变形状况更为接近。 当然，所产生的数据量和测量时间会显著增加。