基于CFD-DEM的高聚物颗粒流化干燥特性研究

王晓静 于 雪

（天津大学化工学院）

流化床干燥器因其高效的传质传热效率、均匀的床层温度分布及灵活的操作条件等优势，广泛地应用于物料的干燥环节。 了解物料在流化干燥过程中的干燥特性对于提高干燥效率、改善干燥系统设计和优化干燥工艺有重要意义。

颗粒的流化干燥机理十分复杂，实验手段往往难以获得气固两相在干燥过程中的详细信息。而随着计算机技术和数值模拟的发展，人们建立了各种数值模型用于模拟气固两相系统， 其中CFD-DEM（计算流体力学-离散单元法）模型所需经验参数较少，可以从颗粒尺度上揭示气固两相的运动和传递特性，成为气固两相系统的研究热点之一［1～5］。

目前有关气固两相传递特性的数值计算，大多集中在热量传递的研究，这对于不存在相变反应的过程是适用的， 而对于物料的干燥过程，必须同时考虑热量和质量的传递。 为此，笔者在上述研究的基础上，引入传质模型，结合CFD-DEM探讨某高聚物颗粒在振动流化床中的失水规律，以期为流化床干燥器的工业应用提供理论依据。

1 数值模型

1.1 流体相模型

流体相模型主要包括连续性方程、 动量方程、能量方程和组分输运方程，分别为：

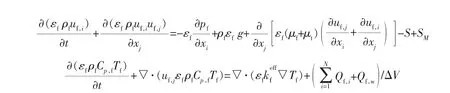
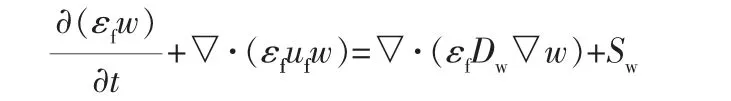
需要说明的是，以上能量方程中的壁面和流体的对流换热通量Qf，w在本研究中不予考虑。

1.2 颗粒相模型

颗粒相模型包括颗粒运动方程和单颗粒能量方程（本颗粒的初始含水率较低，故不考虑干燥过程中颗粒质量和粒径的变化）：

1.3 耦合模型

耦合模型包括Gidaspow曳力模型［8］、Li和Mason颗粒-流体对流传热模型［9］、Batchelor和O′Brien颗粒-颗粒导热模型［10］、水分汽化传热模型和传质模型，为节省篇幅，仅描述水分汽化吸热模型和传质模型，其余模型具体可参见文献［11］。

水分汽化吸热模型为：

单颗粒在无限流体中的传质系数Shi为：

2 模拟对象及计算参数

研究对象为三维矩形振动流化床，结构如图1所示，两侧面为周期性边界。

图1 流化床结构示意图

计算开始前，先在床体上方随机生成一定数量的条状高聚物颗粒，颗粒在重力作用下自由下落，形成一定高度的堆积层。 模拟计算时，流化床以固定振动参数振动，从而使颗粒能够均匀向前运动；床层底部通入热气流，通过改变热气流的温度和流速， 探究颗粒在不同条件下的干燥过程。

3 计算结果与分析

3.1 不同气体流速对干燥特性的影响

图2为气体温度90 ℃和床层高度10 mm时，不同气体流速下物料颗粒的干燥特性曲线（其中，水分比为某一时刻颗粒的含水率与初始含水率之比）。

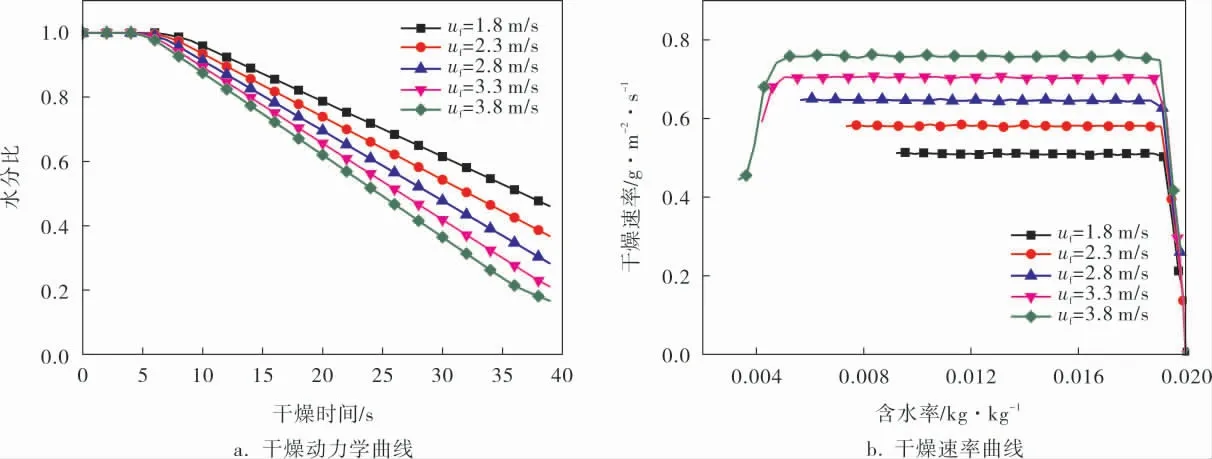
图2 气体速度对物料干燥特性的影响

由图2可以看出，颗粒物料一共经历了预热、恒速干燥和降速干燥3个阶段， 其中恒速干燥阶段所占时间最长，颗粒在恒速阶段的干燥速率随气速的增大而增大，当气体流速由1.8 m/s增至3.8 m/s时， 物料最大干燥速率由0.51 g/（m2·s）均匀提高至0.76 g/（m·s），干燥终了时刻物料的含水率随气体流速的增加而降低， 当气速分别为3.3、3.8 m/s时，颗粒最终含水率低于物料的临界含水率，颗粒进入降速干燥阶段。 其原因主要为，当气速增加时，气流湍动程度增加，对流换热系数增大， 单位时间内从气体传递至颗粒的热量增加，水分蒸发速率随之增大。 其次，气速增加使得颗粒表面的边界层厚度减小，降低了水蒸气向热气流中扩散的阻力，提高了传质效率。 此外，当热空气湿度一定时，气速越大，单位时间内流经颗粒的气体流量越大，且带走的水蒸气就越多，从而维持了颗粒表面与热气流主体间的水蒸气浓度差，有利于干燥过程的进行。

3.2 不同气体温度对干燥特性的影响

图3为气体流速1.8 m/s和床层高度10 mm时，不同气体温度下物料颗粒的干燥特性曲线。 由图3可看出，随着气体温度的提高，颗粒预热时间缩短，干燥速率增大， 达到相同干燥要求时所需干燥时间减少。 当气体温度由95 ℃增加至110 ℃时，颗粒最大干燥速率由0.82 g/（m2·s）均匀地增加至1.74 g/（m2·s）。 其原因主要是气体温度越高，颗粒和气体间的传热温差越大，传热效率越高。 其次，同一气体被加热至更高的温度时， 其相对湿度减小， 因而颗粒表面和热流体间的水蒸气浓度差增大，促进了水分的迁移过程，从而提高了干燥效率。

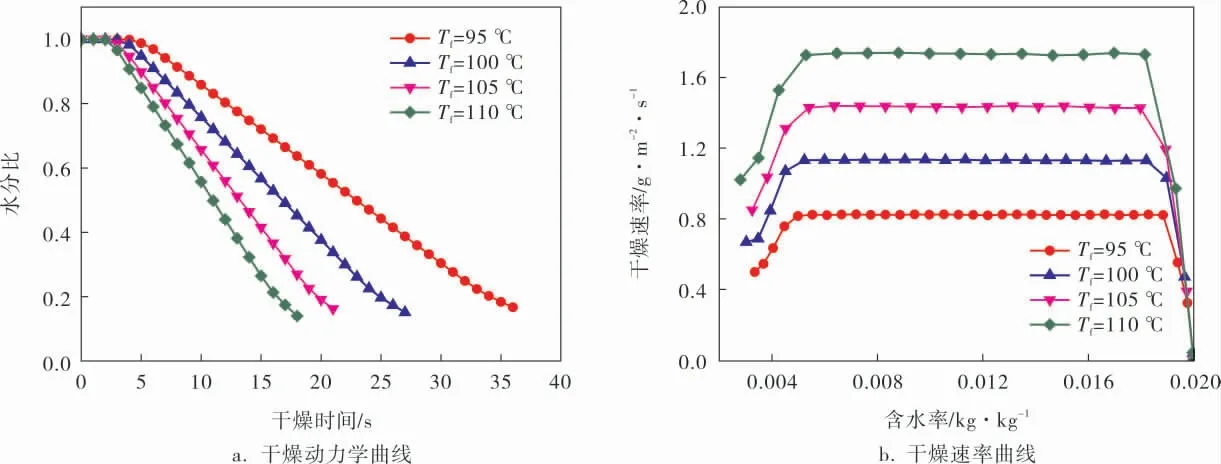
图3 气体温度对物料干燥特性的影响

由图3b可看出，随着气体温度的增大，干燥速率的增长率先增大到一定值后减小。 在预热阶段，颗粒从热气流中吸收热量加热，耗费了一定能量，因此干燥速率较低，不同温度下颗粒的干燥速率变化不大；随着颗粒温度的上升，用于水分蒸发的气体热量增多， 干燥速率不断增大，干燥速率的增长率也逐渐增大，当颗粒温度升至水分蒸发温度时， 气体热量全部用于水分蒸发，因而颗粒干燥效率达到最大值并保持不变，此阶段干燥速率的增长率为一定值；当颗粒表面的非结合水全部蒸发完全时， 颗粒进入降速干燥阶段，干燥过程由内部水分向颗粒表面的迁移速率控制，因而颗粒的干燥速率降低，干燥速率的增长率也随之降低。

3.3 不同粒径对干燥特性的影响

图4为气体速度1.8 m/s、气体温度95 ℃和床层高度25 mm时， 同形状的颗粒在粒径5～8 mm范围内的干燥特性。 由图4可看出，颗粒粒径越小，加热越快，水分蒸发速率越高，随着粒径的增大，其恒速阶段的干燥速率差距逐渐减小，颗粒粒径为5、6、7、8 mm的最大干燥速率分别为0.89、0.78、0.69、0.63 g/（m2·s），在相同干燥时间内，颗粒最终含水率随粒径的增大而增大，即干燥时间随粒径增大而延长。 其原因主要是形状相同的颗粒，粒径越小时，比表面积越大，即传热面积越大，单位时间内传递的热量增加，水分蒸发加快。 其次，粒径越小，颗粒内部的自由水能够及时传递至颗粒表面， 维持表面的润湿状态，从而使颗粒保持较高的干燥速率，缩短干燥时间。

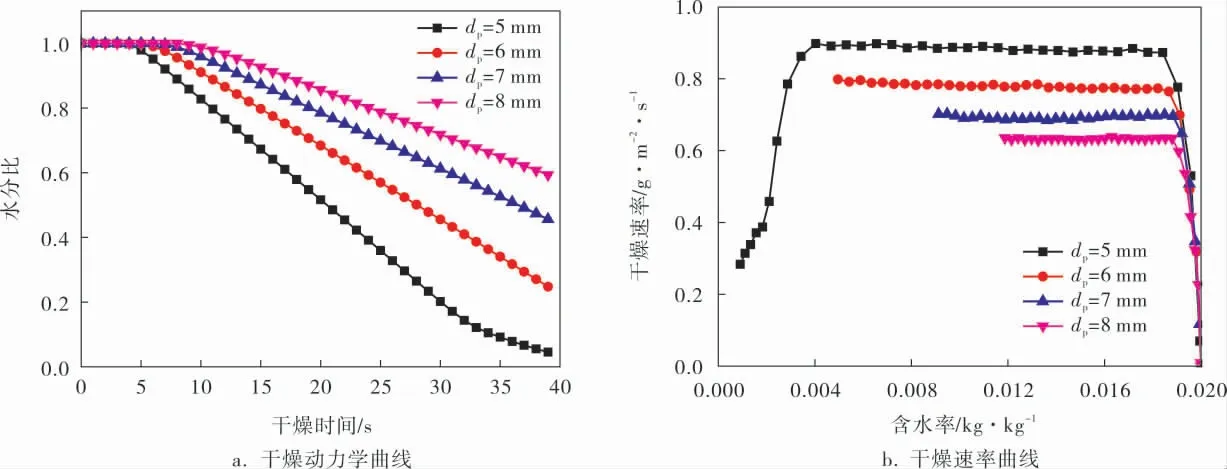
图4 颗粒粒径对物料干燥特性的影响

图5展示了不同时刻床层内颗粒含水率的变化情况。 由图5可看出：不同粒径颗粒均匀分布在床层中，从总体上看，床层含水率从顶层向底层递减； 对于同一粒径颗粒， 越接近床层底部，含水率越低；对于不同粒径颗粒，颗粒粒径越小，含水率越低，与其所处床层位置无关，由此说明， 颗粒粒径对干燥速率的影响比床层位置更为显著。

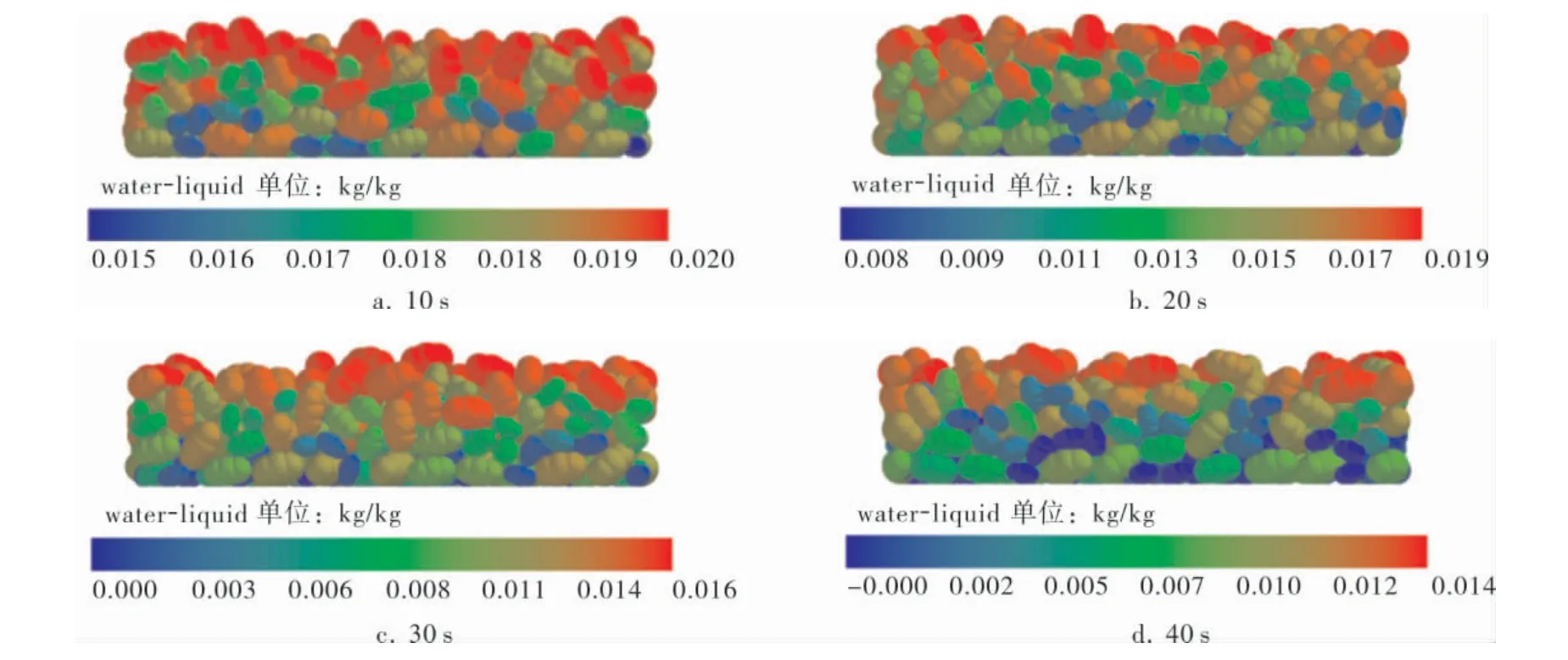
图5 不同时刻颗粒含水率变化

4 干燥动力学模型

以气体流度1.8 m/s、气体温度95 ℃和床层高度10 mm的干燥工况为例，选用5个常见的薄层干燥动力学模型［12，13］对模拟数据进行拟合，拟合结果见表1。 拟合后，采用相关系数R2、卡方值χ2和均方根误差（RMSE）作为数学评价指标，其中，R2越接近于1、χ2和RMSE越低， 说明该模型的拟合效果越好。

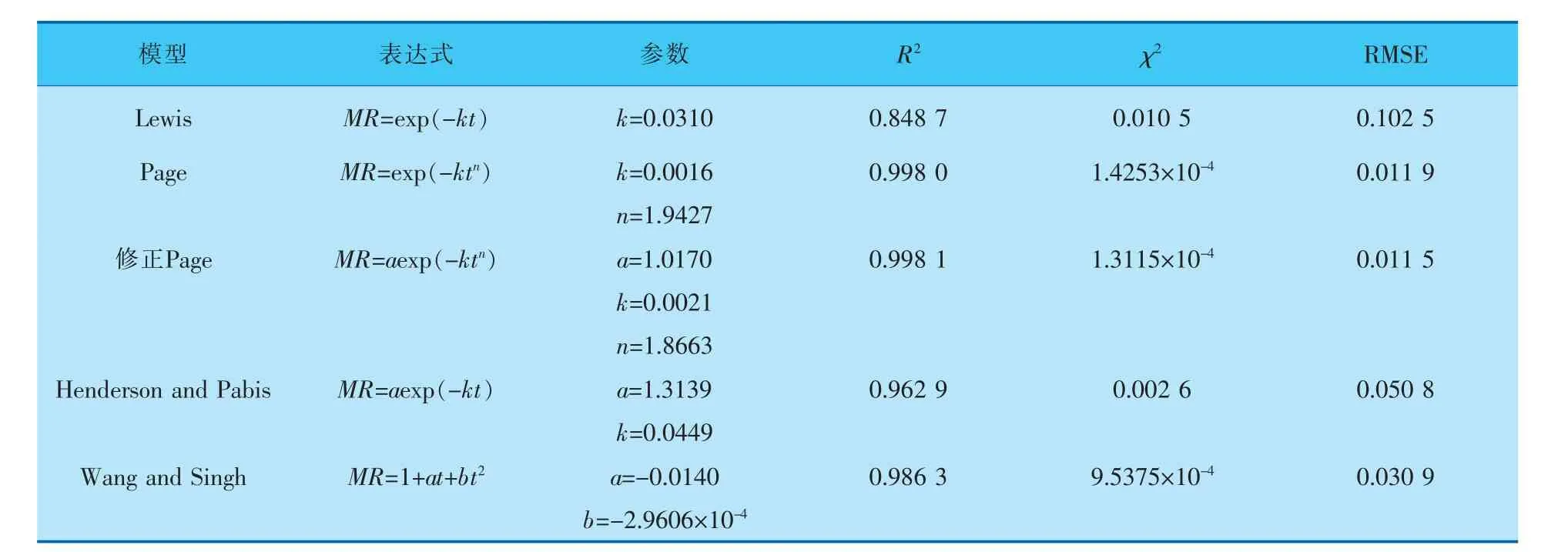
表1 不同干燥动力学模型的拟合参数

由表1可知， 修正Page模型的拟合效果最好，拟合得到的模型参数a=1.0170、k=0.0021 和n=1.8663，评价指标为：相关系数R2=0.9981、卡方值χ2=1.3115×10-4、均方根误差（RMSE）为0.011 5。

5 结论

5.1 颗粒干燥过程主要发生在恒速干燥阶段，随着气体的流速和温度提高，气固两相间的传热和传质效率均提升，颗粒干燥速率增大，达到相同干燥要求时所需干燥时间减少。

5.2 颗粒粒径对干燥速率影响显著，随着粒径的增大，颗粒干燥速率降低，干燥时间延长。 对于同一粒径颗粒，越接近床层底部，含水率越低；对于不同粒径颗粒，颗粒粒径越小，含水率越低，与所处床层位置无关，可以确定颗粒粒径对干燥速率的影响比床层位置的影响更加显著。

5.3 选用常见的薄层干燥动力学模型对模拟数据进行拟合，发现MR=aexp（-ktn）模型能够很好地描述颗粒的失水规律，其评价指标分别为相关系数R2=0.9981、卡方值χ2=1.3115×10-4、均方根误差（RMSE）为0.011 5。