螺栓轴向力对发动机机体组件的影响

李义，杨晶，刘永进

山河智能装备股份有限公司 国家企业技术中心，湖南 长沙 410100

0 引言

机体安装着发动机所有主要零件与附件，是发动机的骨架和外壳。发动机工作过程中，机体承受着大小和方向周期性变化的气体力、惯性力和力矩的作用，为保证发动机可靠和耐久地工作，机体必须有足够的强度与刚度。在发动机的开发及结构设计中，机体及主要零部件的有限元分析至关重要。张瑞波等[1]研究表明，螺栓轴向预紧力对机体模态频率与振动位移影响很大；杨万里等[2]研究表明，机体主轴承座分工况并采用不同的计算模型可保证仿真结果的可靠性；曹茉莉等[3]研究表明，螺栓凸缘结构的改进可以改善机体圆滑过渡部位的应力分布；杜建红等[4]研究表明，采用分层次的特征模型可以方便的对机体结构进行简化处理。

本文中利用有限元分析软件，根据发动机总体性能要求初步确定2种规格的螺栓，对机体进行仿真分析、经验计算与拧紧试验，分析机体内部零部件的应力分布，计算接触面正应力，并根据分析计算与试验结果来判定螺栓性能。

1 有限元模拟分析计算

1.1 模型建立及网格划分

发动机机体模型对有限元分析结果影响很大，本文中对某直列四缸、缸内直喷汽油发动机机体进行研究，发动机主要技术参数如表1所示。

表1 发动机主要技术参数

机体的结构尺寸大，如果对整个机体模型进行模拟分析计算，需要划分大量网格，花费大量时间；机体上分布着大量的加强筋、螺纹孔、水道与倒角等，如果将这些复杂结构均导入模型中，网格将发生畸变，网格质量下降，影响求解精度。综合考虑有限元模型的计算规模及计算精度，根据圣维南原理，对某些局部特征进行简化：1)选取中间完整单缸和相邻2个半缸进行分析，主轴承壁只承受周围2缸的机械载荷，为了保证模型相对完整性，将相邻两侧的2个半缸也作为研究对象；2)忽略机体内部细小加强筋、螺纹孔、水道与倒角。

高质量的网格是仿真分析结果准确的关键，网格划分应兼顾网格数量、质量和网格的疏密分布。机体存在质量分布不均匀和应力集中，需要对结构突变的部位进行网格加密处理；机体内部不同零部件之间的接触存在复杂的非线性问题，应对接触部位进行局部网格加密以提高计算的收敛性[5]。

对机体、主轴承盖的应力和变形的仿真分析采用十节点二次四面体单元，螺栓、滑套的应力和变形采用八节点线性六面体单元。整个模型的单元类型、单元数与节点数如表2所示，划分网格后机体有限元模型如图1所示。

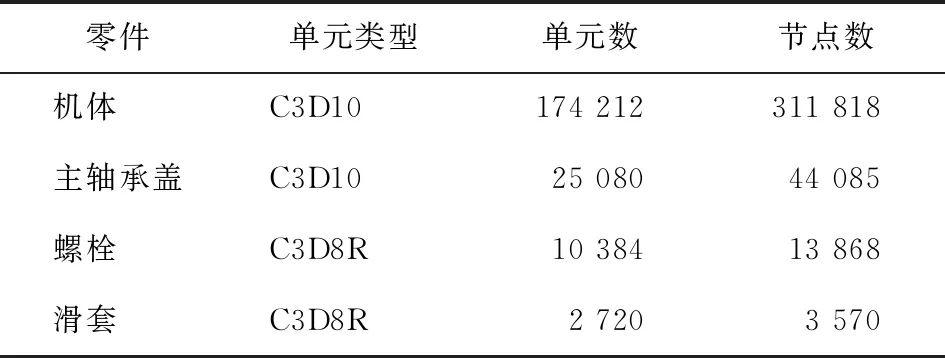
表2 机体各零部件的单元类型、单元数与节点数

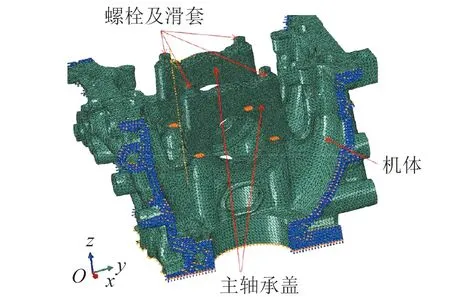
图1 简化后的机体网格模型

1.2 材料与载荷边界条件

在满足发动机总体性能要求下，机体材料及备选螺栓规格参考现有市场上成熟的机型进行选择，缸体、主轴承盖及滑套材料属性及数量如表3所示。

表3 各零件材料属性及数量

选用M10×1.5-10.9和M10×1.5-12.9 2种规格的螺栓各10个进行计算分析。载荷边界条件与工程实际的吻合程度直接影响计算结果的准确性与合理性。设计时，主轴承盖螺栓拧紧力矩应满足螺栓应力、应变处于屈服阶段的需求。根据转矩-转角法过屈服条件计算得到螺栓轴向力[6-8]，2种等级主轴承盖螺栓材料的机械性能参数及轴向力计算结果如表4所示。

表4 2种规格螺栓的机构性能参数及轴向力计算结果

1.3 约束与接触边界条件

机体属于对稳态问题的求解，最常见的边界约束条件是位移约束，通过限制结构各个方向自由度，使得计算方程有唯一解，将机体顶面六个自由度全部限定，可以精确模拟发动机对机体的支撑作用。由于机体内部零件之间相互接触，2个接触面的相对位移随载荷的变化发生典型的非线性变化，非线性问题在计算中花费大量时间，任何一处接触参数设置不合理都可能导致平衡方程求解困难，所以应针对性地设置接触，本文中计算对象的接触行为包括绑定与小滑移接触2种方式。具体接触设置方式表5所示。

表5 内部零件接触关系表

本文中采用增广型拉格朗日法进行接触分析，在拉格朗日法的基础上，增加一个惩罚强迫项，使其满足特定的关键约束，既吸收了罚函数法和拉格朗日法的优点，又不增加系统求解规模[9-10]。

采用增广型拉格朗日法计算时，接触区域方程为：

(1)

式中：δπ为接触区域的总位能，J；δ为位能函数；λ为拉格朗日乘子，m2；γN为接触渗透率，m2；α为罚函数项；ΓC为接触面积区域；Γ为接触面积，m2。

接触有限元计算的控制方程为：

Ma+fint-fext+GTλ+Pcd=0，

(2)

式中：Ma为惯性力，N；fint为内力，N；fext为外力，N；GT为接触压强，Pa；Pc为接触刚度，N/m；d为位移，m。

2个接触面之间的约束边界条件为：

▽G≤0，

(3)

式中▽G为剪切模量的梯度。

1.4 模型求解及分析

根据上述载荷与约束边界约束，对机体组件进行有限元分析。机体有限元分析结果如图2所示。

a)10.9级螺栓 b)12.9级螺栓

由图2可知：2种螺栓在屈服拧紧条件下，最大应力出现在与主轴承座结合面附近，分别为75 MPa与93 MPa，材料不会失效。

主轴承盖有限元分析结果如图3所示。由图3可知：2种螺栓在屈服拧紧条件下，最大应力出现在与螺栓连接处，分别为156 MPa与192 MPa,材料不会失效。

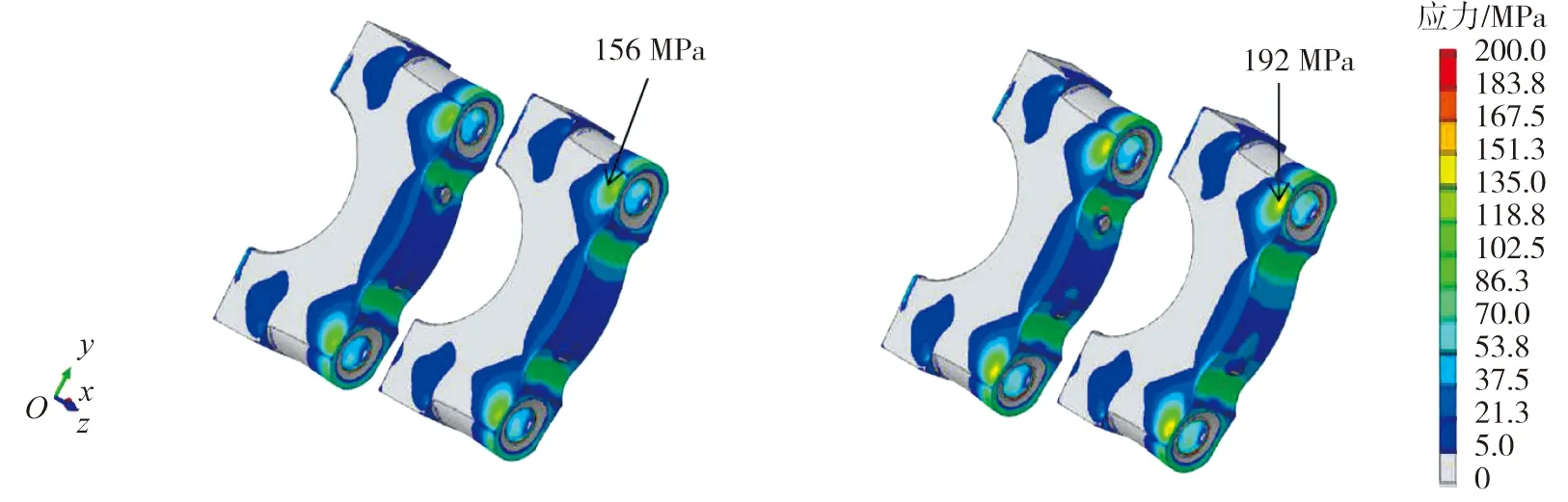
a)10.9级螺栓 b)12.9级螺栓

滑套有限元分析结果如图4所示。由图4可知：2种螺栓在屈服拧紧条件下，最大应力出现在中部位置，分别为265 MPa与312 MPa，材料不会失效。

a)10.9级螺栓 b)12.9级螺栓

接触正应力取决于接触正压力与接触面积，计算公式为：

p=F/A，

(4)

式中：p为接触应力，MPa；F为接触正压力，N；A为接触面积，mm2。

依据式(4)，基于屈服拧紧条件下接触正应力计算结果如表6所示。

表6 不同性能等级螺栓的接触正应力计算结果

由表7可知：12.9级螺栓-主轴承盖之间的接触正应力为529 MPa，高于材料的接触许可应力500 MPa的要求，存在失效的风险。

2 试验验证

验证试验在机体-主轴承盖螺栓专用拧紧机上进行，台架试验现场如图5所示。采用转矩-转角控制过屈服拧紧法进行试验，该方法具有螺栓轴向预紧力精度高的优点，可以获得较大的螺栓轴向预紧力。试验过程为：将机体倒置固定在拧紧机工作台上，拧紧机开始工作，拧紧过程中螺栓转矩不断增大，当转矩达到设定的转矩(30 N·m)时，将拧紧机轴控单元内部的螺栓转角计数器清零，然后立即开始对螺栓转角计数，当螺栓转角达到设定值(90°)时，轴控单元立即向电机驱动器控制模块发出信号，控制模块向电机控制器发出指令，伺服电动机停止工作，完成本次拧紧工作。

图5 机体主轴承盖螺栓拧紧机试验台架

试验结果表明：M10×1.5-10.9主轴承盖螺栓拧紧后，机体零件各部位未出现任何失效，与有限元分析及经验计算结果一致；M10×1.5-12.9主轴承盖螺栓拧紧后，8处螺栓-主轴承盖接触对的主轴承盖一侧出现轻微压溃现象，其余部位未出现失效，也与有限元分析及经验计算结果一致；另外2处螺栓-主轴承盖接触对主轴承盖一侧未出现压溃。经分析原因为：拧紧机拧紧后，虽然10处主轴承盖螺栓最终的监控转矩基本一致，但由于机体制造工艺上的差异，螺栓拧紧转矩最终转化为螺栓轴向力不完全一致，2处主轴承盖一侧未出现压溃，可以认为螺栓拧紧转矩更多地作用在克服零件间的摩擦转矩上，较少地转化为螺栓轴向力。

3 结论

1)对2种不同规格主轴承盖螺栓的机体进行分析计算，采用增广型拉格朗日法仿真分析机体零部件之间的相互作用并建立了有限元模型，依据经验公式计算了接触面正应力。模拟分析与经验计算和试验结果基本一致，充分证明了本次分析计算的正确性与合理性。

2)分析计算结果表明，缸体、主轴承盖与滑套的最大应力均低于材料抗拉强度的要求，没有失效。M10×1.5-10.9螺栓在屈服拧紧条件下，机体零件各部位未出现任何失效情况，符合发动机对螺栓的性能需求。M10×1.5-12.9螺栓在屈服拧紧条件下，螺栓-主轴承盖接触对主轴承盖一侧出现轻微压溃情况，需要对机体相关零部件结构、材料进行优化，才能满足发动机要求。