基于Fluent的微孔过滤器内部流场的数值模拟

杨朝忠，朱成杰，刘伟男，赵茂俞

(1.合肥学院 生物食品与环境学院，安徽 合肥 230601；2.合肥学院 先进制造学院，安徽 合肥 230601)

1 引言

微孔过滤技术广泛运用于污水的净化处理过程中，针对水处理过程中的泥沙、铁锈等悬浮颗粒物，在过滤过程中，先进行介质过滤，即固体颗粒的直径大于过滤微孔孔径，在过滤孔表面形成固体颗粒沉积层，即架桥现象产生，进而微孔过滤往往可以过滤许多比微孔孔径更小的杂质，达到更高的过滤效率[1]。利用这一现象，越来越多的微孔过滤器应用于家庭用水的净化处理中，其中过滤效果是微孔过滤器的一个重要指标，而过滤效果受流速、微孔孔径、粒径等因素的影响[2]。

Fluent是当今比较通用的一种计算流体力学(CFD)的软件，它含有基于压力和密度的求解器，用以达到最快的收敛速度和最精确的求解精度，并具有丰富且成熟的物理模型，如湍流模型、多相流模型、离散相模型、辐射模型等，以匹配不同工况下的流场数值模拟，Fluent中强大的网格处理技术保证了仿真前处理的可靠度，后处理技术可以对数据进行可视化图形处理和图标生成[3,4]。因此，运用Fluent进行数值模拟在解决在多相流问题、湍流流动、化学反应和燃烧问题等方面具有广泛的应用。

本文利用CFD软件中的Fluent仿真软件对不同工况下微孔过滤器的过滤效率进行数值模拟，在不同微孔孔径、孔间距和流速下的装置内部的流场运动规律[5]。

2 计算模型

微孔过滤器过滤为水流流动携带有泥沙、铁锈等颗粒物经过微孔金属网的过程，为了研究过滤过程中的内部流场变化，由于水流的流动属于不可压缩流动，且泥沙等颗粒在水流中的体积分数较小，本文构建了湍流模型和离散相模型。

2.1 湍流模型

(1)

扩散方程：

(2)

式(1)、(2)中，Gk表示由平均速度梯度引起的湍流动能，J；Gb表示由浮力产生的湍流动能，J；Ym表示可压缩湍流中波动膨胀对总耗散率的贡献；C1ε、C3ε为经验常数，取1.45和1.92；σk是k方程的普朗特数取1.0；σε是ε方程的普朗特数取1.3；Sk、Sε是自定义源项；k为湍流动能，J；ε为湍流动能耗散率；μ为层流黏性系数，m2/s；μt为湍流黏性系数，m2/s[7,8]。

2.2 离散相模型

Fluent 中的离散相模型一般适用于颗粒相体积小于10%且具有明确的入口和出口，通过计算连续流场和变量求解每一个颗粒的受力情况，在本案中水中的固体颗粒的体积分数小于10%，在水流携带颗粒流动时，颗粒与颗粒之间的相互作用和颗粒对于水流的影响不加以考虑，可以用离散相模型来模拟实际的情况[9,10]。

颗粒作用力平衡方程：

(3)

(4)

(5)

(6)

式(3)～(6)中：u为流体相速度，m/s；up为颗粒速度，m/s；μ为流体动力粘度，Pa·s；ρ为流体密度，kg/m3；ρp为颗粒密度，kg/m3；dp为颗粒直径，m；Re为相对雷诺数；a1、a2、a3为常数；FD为单位质量曳力，N；CD为曳力系数；gx为x方向重力加速度，m/s2；Fx为x方向其他作用力，N[11]。

3 几何模型及划分

3.1 模型结构简化

微孔过滤器主要依靠内部的微孔过滤网对水中的悬浮物杂质进行截留，使其截留的杂质通过排污口流出，从而获得更加纯净的水质。微孔过滤器的装置结构如图1所示。

图1 微孔过滤器的装置结构

为了更加直观地了解微孔过滤器内部的压力情况，可以对微孔过滤器的模型进行简化，将微孔过滤器内部的微孔过滤网简化为单一的二维微孔面，在Fluent的前处理软件Gambit中建立模型，简化后的模型如图2所示。

图2 简化后的二维模型

简化后的模型为二维模型，长度1 mm，高度0.32 mm，微孔之间的孔间距为0.02 mm，用来模拟在上述尺寸下微孔过滤器内部的压力流场情况。

3.2 边界设定

根据模型的特点和计算条件，由于微孔过滤模型属于不可压缩流动，将入口条件设为速度进口，定义流动入口边界的速度和标量；出口设为出口流动，用来模拟未知的出口速度和压力情况；微孔过滤板设置为wall,用于限制流体和固体区域[12,13]。

3.3 网格划分

在Gambit中进行对模型的网格划分，定义网格类型、步长等，为了使仿真结果更加精确，在进行网格划分时，对靠近壁面的空间处和远离壁面的空间处要进行不同种类的网格划分，由于模型为规则的四边形，选择Map网格，生成四边形的结构性网格，提高了计算效率[14,15]。

4 仿真模拟

分别改变通过孔径、流速、粒径的自变量，保证其余的控制变量不变，获得内部流场的压力流场图，通过对比流场图的颜色深浅，直观地感受到压力变化。

4.1 微孔孔径对内部流场的影响

给定一组射流，流速为5 mm/s，水流中加入直径为20 μm的颗粒，将上述的水流通入以下3 种模型中，孔径30 μm，孔间距20 μm的模型，其压力变化如图3所示。

图3 孔径30μm压力云图

孔径40 μm，孔间距20 μm的模型，其压力变化如图4所示。

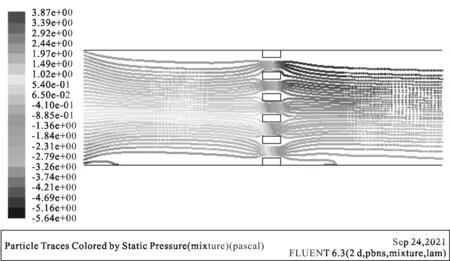
图4 孔径40 μm压力云图

孔径50 μm，孔间距20 μm的模型，其压力变化如图5所示。

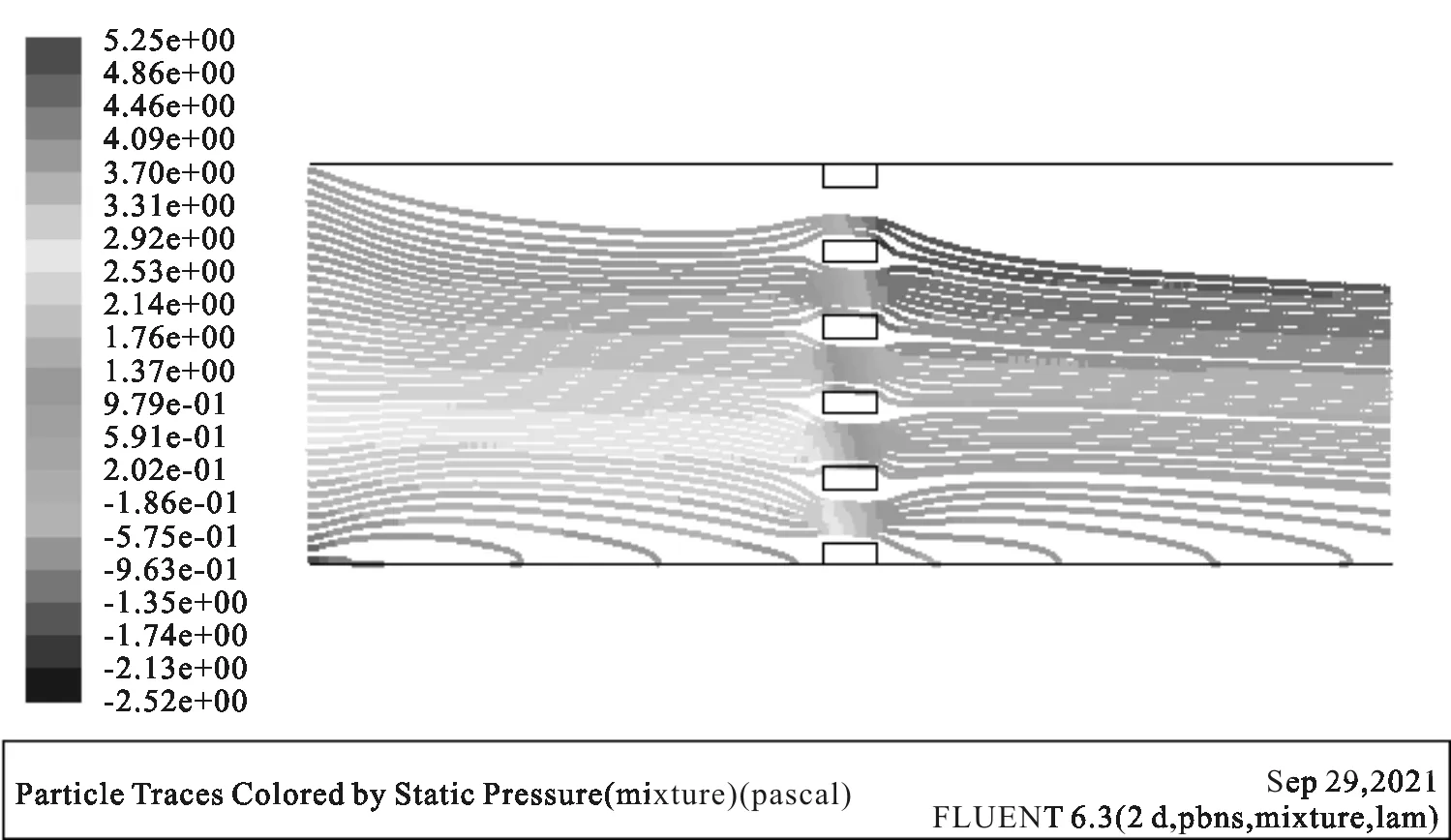
图5 孔径50 μm压力云图

对比不同孔径下的模型内流场的情况，由图3、图4、图5的压力流场图可知，含颗粒的射流经过微孔网上产生一定的压降，且微孔孔径越大，产生的压降越小，根据追踪粒子的路径可知，捕集率也随着孔径的增大而减小。

4.2 流速对内部流场的影响

给定一组射流，流速为5 mm/s，水流中加入直径为20 μm的颗粒，将上述的水流通入以下3 种模型中，孔径40 μm，孔间距20 μm的模型，其压力变化如图6所示。

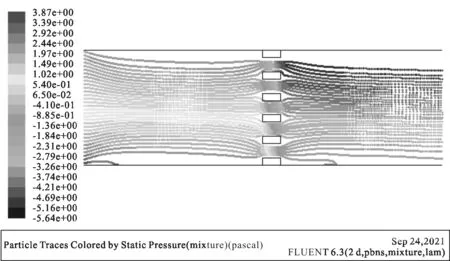
图6 流速5 mm/s压力云图

流速3 mm/s含直径 20 μm的颗粒的射流，通入孔径40 μm，孔间距20 μm的模型，其压力变化如图7所示。

图7 流速3 mm/s压力云图

流速2 mm/s含直径20 μm的颗粒的射流，通入孔径40 μm，孔间距20 μm的模型，其压力变化如图8所示。

图8 流速2 mm/s压力云图

从图6、图7、图8的压力流场图可以看出，流速5 mm/s的射流粒子在经过微孔网上产生的压降大于3 mm/s和2 mm/s产生的压降，即射流的流速越大，产生的压降越大，根据追踪粒子的路径可知，捕集率也随着速度的增大而减小。

4.3 粒子直径对内部流场的影响

在流速5 mm/s的射流中加入直径20 μm的离散相颗粒，将水流通入孔径40 μm，孔间距20 μm的模型，其压力变化如图9所示。

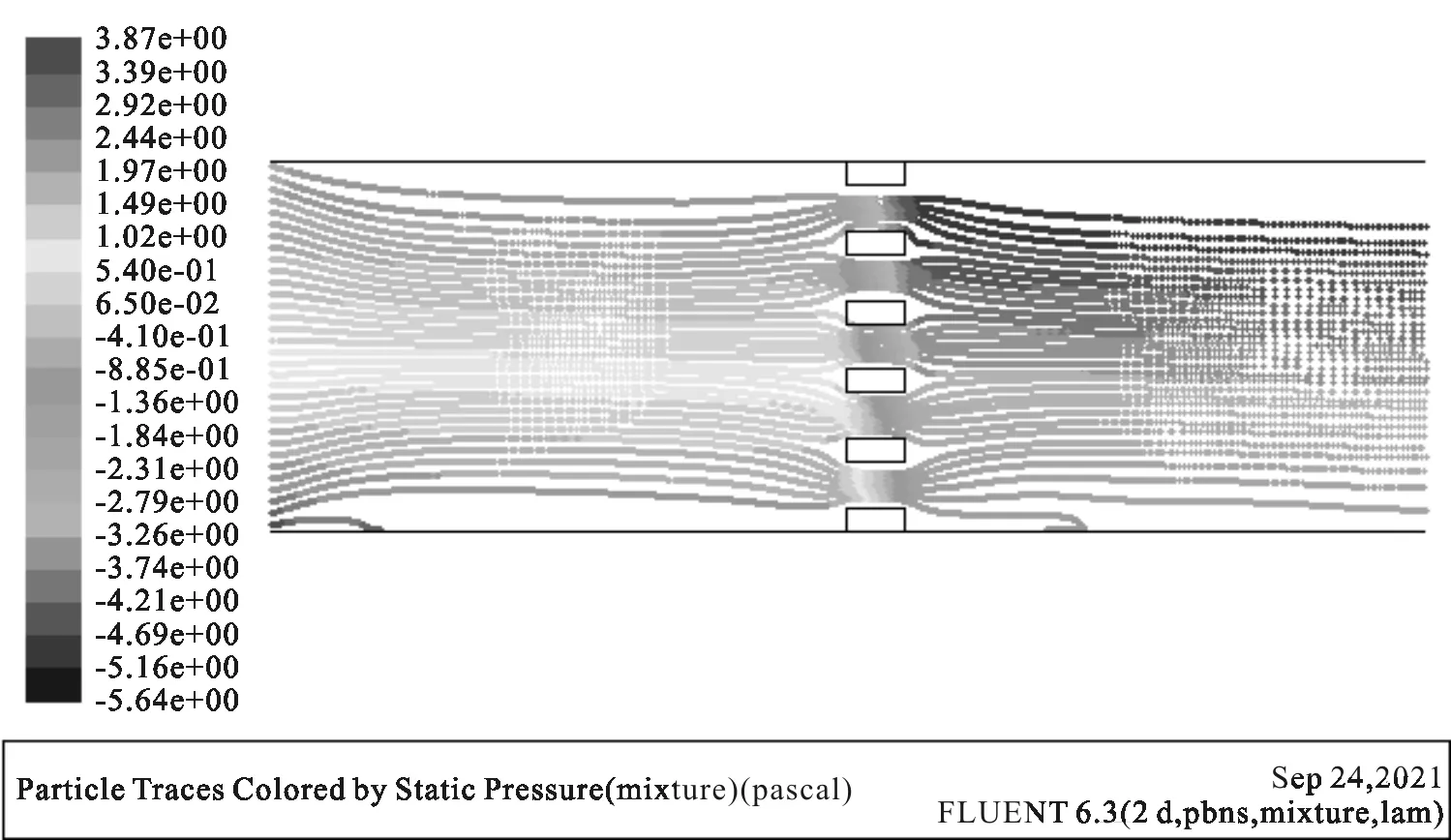
图9 粒径20 μm压力云图

在流速5 mm/s的射流中加入直径25 μm的离散相颗粒，将水流通入孔径40 μm，孔间距20 μm的模型，其压力变化如图10所示。

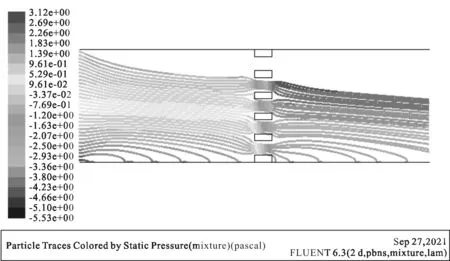
图10 粒径25 μm压力云图

在流速5 mm/s的射流中加入直径30 μm的离散相颗粒，将水流通入孔径40 μm，孔间距20 μm的模型，其压力变化如图11所示。

图11 粒径30 μm压力云图

由图9、图10、图11的压力流场图可知，含射流内的粒子直径越大，对内部流场的压降的影响不大，根据追踪粒子的路径可知，粒径30 μm的射流的粒子逃逸的数目最少，即捕集率随着粒子直径的增大而增大。

5 结果讨论

在不同的孔径、流速、粒径条件下，数值模拟了微孔过滤器的内部流场，研究了各因素等对压力和捕集率的影响。获得了以下的结论。

(1)在过滤过程中，相同的流速和粒径下，微孔孔径越大，则产生的压降越小，粒子的逃逸数目越多，即捕集率越小。

(2)在其他条件相同情况下，水流的流速越快，产生的压降越大，粒子的逃逸数目越多，即捕集率越小。

(3)在其他条件相同情况下，粒子的直径越大，对压力的影响不大，而粒子的逃逸数目越少，即捕集率越大。