基于数据挖掘技术的水质自动监测仪故障诊断及预测

李汉汉

(广东青创环境检测有限公司，广东 江门 529000)

1 引言

水质自动监测仪可以实现水质的自动实时监测，检测基本水质参数和各种重金属的浓度，将连续的自动采样技术与云技术相结合，将监测的水质结果自动回传到云服务器，解决了人工采样在采样频率和采样强度方面进行实时监测的困难。但是水质自动检测仪设备需要进行定期的故障检测，以便维护设备的正常工作。

2 故障诊断技术研究现状

在设备的故障检测研究过程中，有以傅里叶变换为代表的信号处理方式，通过提取时域特征来检测设备出现故障的部件[1]，但是只使用傅里叶变换的信号处理方式会出现信号损失等问题，进一步影响检测的精度。韩金鹏[2]采用粒子群算法优化随机森林，结合LightGBM(Light Gradient Boosting Machine)设计了一种故障检测方法，主要运用了随机森林用于特征选择的思想。张建永[3]在物联网环境系统中采用BP神经网络，提出了一种物联网系统故障诊断方案[4]。由以上的研究方法中可以得知，数据挖掘方式的故障检测方案可以提高预测分类和故障分类的准确率，基于数据挖掘的故障监测方案逐渐成为研究的主流方向。

3 故障部件识别

本方案将对振动数据进行分析，以识别故障部件。水质自动检测仪的常见故障主要有：蠕动泵损坏、多通道阀漏液、光电计量器损坏、外接泵堵塞、高压阀漏气和测量室损坏。

3.1 数据预处理

在实际环境中，水质自动监测仪的数据可能会有一些杂乱的无效数据，或者有些数据丢失，这都会对诊断和预测模型的建立产生影响[5]，因此收集到监测数据，需要进行预处理。本研究中使用的数据是由NREL提供的，共同目标是提高监测仪的总体可靠性。本研究中使用的监测仪额定功率为750 kW，数据在高频(即40 kHz)下采样，并在受控测试条件下记录10 min。

首先，通过计算Jerk来确定振动对不同传感器位置的影响。“Jerk”被定义为加速度的变化速率。数学上，Jerk近似表示如式(1)所示：

(1)

使用10 min过程中12 个振动传感器数据的平均Jerk值，初始40 kHz数据的平均间隔超过15 s。对振动波形进行统计分析，计算了如RMS、CF和峰度(Ku)等指标。

3.2 频域分析

从传感器AN4获得的数据在频域内进行了分析，快速傅里叶变换(FFT)已被用来产生振动的频谱。频谱显示位于给定频率的振幅部分(以g表示)，在高速轴上测量的基线光谱如图1所示。

图1展示了在36.45 Hz下的低能量(<0.035 g)成分，由于HSS包含高达20 kHz的光谱，因此只显示低频分量(即0～100 Hz)，以更好地说明信号功率。

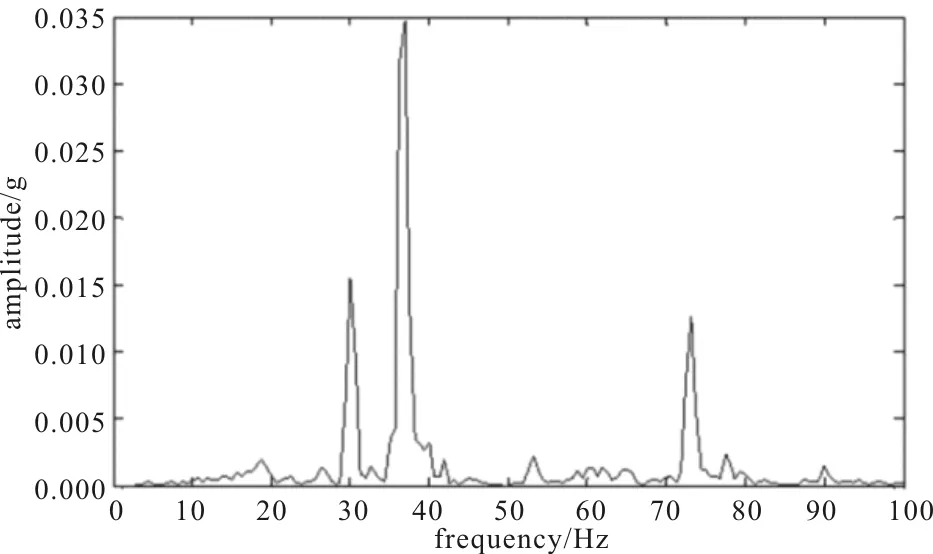
图1 正常状态的基线频谱

图2显示了整个测试运行(第1～10 min)的功率谱趋势，该功率谱在不断增加，表明了故障的进展情况。

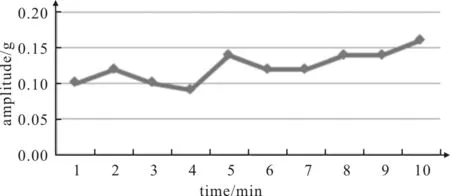
图2 振幅的趋势

4 用于预测故障的模型

基于可用的数据，开发了4 种场景。方案1称为单参数预测模型，其中加速度值是目标输出，而输入参数包括历史加速度值。在场景2 中，来自AN4 以外的传感器的数据被用作输入来预测AN4的加速度。场景3 和场景4 与场景1 和场景2 相同，除了Jerk是目标输出。统计指标(即平均值、最大值、标准差、波峰因子、峰度、RMS、间隙因子)也被包含在输入参数中，以预测目标输出。为了降低数据集的维数，将初始高频数据(即40 kHz)转换为10 Hz的数据。对于每个模型，80%的数据点用于构建模型，然后在接下来的10%上进行测试，利用在测试数据集上证明最佳结果的算法对最后10%的数据进行预测。

4.1 参数选择

采用不同的参数选择算法来识别预测水质监测仪振动的相关参数，本方案选择提升树(Boosting Tree)、Relief Attribute(k=10)和子集评估器3种算法进行分析[6～8]。增强树算法根据误差的平方和生成参数排序，并在输入参数的每次分割处计算，计算所有分割的误差的平均平方和，具有最佳分割的参数值为1，以此类推。在提升树算法中，参数的相对影响采用公式(2)进行计算：

(2)

符号AANi表示神经网络预测加速度，而JANi表示神经网路预测Jerk，i是传感器位置下标。对于单参数模型(即场景1和场景3)，(t-k)表示目标输出的历史值，k表示时间指数。利用参数选择算法生成的参数集，输入参数包括目标输出的存储器参数和在AN4 以外的传感器位置记录的参数。针对场景1～4的数据的初始维度为60，使用参数选择算法，将场景1、2、3和4的维数分别降至14、16、18和18。

4.2 算法与场景选择

由于各种传感器之间的功能关系是未知的，因此对具有不同参数设置的多层感知器(MLP)进行了优化，以获得4 种模型的最佳网络。不同的神经网络被用于训练，而隐藏单元的数量在5～25 个之间变化。分析了隐藏节点和输出节点的激活函数，即Tanh、指数节点、恒等式和逻辑节点。在本研究中，用了绝对误差(AE)、平均绝对误差(MAE)、相对误差(RE)和平均相对误差(MRE)等指标来选择最佳的神经网络，相关指标计算公式如下。

(3)

(4)

(5)

(6)

4.3 神经网络训练算法的选择

分析了神经网络训练算法，如梯度下降(GD)、共轭梯度(CG)和径向基函数(RBF)。加速度数据(场景1)用于评估这些神经网络训练算法的性能。测试表明，相比于其他神经网络算法，BFGS-NN(Broyden-Fletcher-Goldfarb-Shanno)算法与实际输出具有更高的相关性[9～11]。

与GD、CG和RBF神经网络等算法相比，BFGS神经网络在MAE方面分别提高了17.39%、12.63%和17.7%。而在MRE方面，分别提高了16.6%、12.22%和17.00%。这就证明了使用BFGS作为神经网络算法来构建模型的合理性[12]。

BFGS使用一种近似搜索方案来提高计算速度并实现全局收敛，它包括以下四个基本步骤：①设置搜索方向；②沿着搜索方向确定步长；③更新Hessian矩阵；④使用指定的标准检查收敛速度。

通过改变神经元数量、隐藏激活函数和输出激活函数，随机选择100 个神经网络。所有100 个NNs都采用BFGS算法进行训练、。该过程重复5 次，每次迭代时选择最佳的NN，使用测试数据进行性能比较。在隐藏层和输出层中具有Tanh函数的MLP14-5-1 最适合场景1。以Tanh为例的MLP16-18-1，Tanh作为隐藏激活函数，逻辑函数作为输出激活，最适合场景2。对于基于Jerk数据的模型，以Tanh和指数函数分别为隐藏函数的MLP18-22-1 最适合场景3；而以指数和身份函数为隐藏和输出激活的MLP18-22-1适用于场景4。

Jerk模型中的神经网络比基于加速数据的模型产生更好的结果。这说明Jerk更适合于构建不同时间戳下的预测模型。在Jerk模型中，模型4的结果优于模型3，说明了其他传感器在预测振动中的重要性[13]。

5 计算结果

使用性能最好的神经网络模型(MLP-18-22-1)进行预测，该模型使用来自传感器位置AN1-AN3和AN5-AN12的数据来预测Jerk(由传感器AN4测量)[14]。因为本研究中使用的数据记录时间很短(例如，10 min)，Jerk预测15 个时间戳，数据间隔为0.1 s采样。MAE的范围在0.021～0.345 之间，而MRE的范围为5.21%～8.32%(图3)。

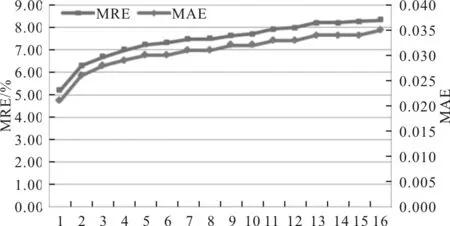
图3 不同时间戳的MAE值和MRE值

图3显示了15个时间戳的MAE和MRE值，MAE和MRE的值随着时间的推移而增加。前期预测的结果离散度较小，而在后期的时间戳预测中，结果离散度较大[15]。图3所示的结果表明，所提出的方法能够准确预测对部件故障影响最大的Jerk值。

6 结语

本文提出了一种识别和预测水质监测仪故障的方法。利用Jerk和加速数据，用数据挖掘算法生成模型。基于单个传感器(AN4)和多个传感器(AN1-AN3和AN5-AN12)的数据，分析了4 种不同的模型，单个传感器模型假设只安装了一个传感器，而多个传感器模型预测了选定的传动系位置的振动。使用Jerk数据开发的数据挖掘模型(场景3和4)比基于加速数据(场景1和2)生成的模型具有更好的精度，利用基于多个传感器数据开发的模型(方案4)进行Jerk预测，使用BFGS学习方法的神经网络的性能优于CG、GD和RBF等算法。BFGS神经网络模型准确预测了不同时间间隔的Jerk，MAE在0.021～0.345范围内，MRE在5.21%～8.32%范围内。