主梁刚度对下承式钢桁架拱桥静力特性的影响分析

作者简介：

李运浦（1993—），硕士，工程师，主要从事土木工程方面相关工作。

摘要：文章以某下承式钢桁架拱桥为例，通过采用Midas Civil有限元软件建立实桥模型，研究了不同主梁刚度变化时下承式钢桁架拱桥的静力特性变化规律，得出以下结论：（1）随着主梁刚度的增大，下承式钢桁架拱桥主梁最大拉应力、压应力均逐渐增大;（2）拱肋上弦杆1/4截面受主梁刚度的影响较小，下弦杆拱脚截面受主梁刚度的影响较大;（3）随着主梁刚度的增大，钢桁架拱桥主梁竖向位移、拱肋位移及吊杆索力均逐渐减小，主梁刚度的增大能够有效减小主梁竖向位移，主梁刚度对拱梁相交处吊杆索力的影响大于跨中处。

关键词：下承式钢桁架拱桥;主梁刚度;应力;位移;索力

中国分类号：U448.53A381384

0 引言

由于钢桁架拱桥具有自重轻、体积小、造型美观、坚固耐用等优点，在大跨度桥梁建设工程中得到了广泛的应用[1-2]。在钢桁架拱桥设计阶段中，主梁刚度是需重点关注的参数之一，其对桥梁结构受力稳定及变形至关重要[3-5]。本文以某下承式钢桁架拱桥为例，通过采用Midas Civil有限元软件建立实桥模型，针对不同主梁刚度变化下钢桁架拱桥的静力特性变化规律进行了系统研究，以期为同类桥梁的设计及施工提供参考与借鉴。

1 工程概况

某下承式钢桁架拱桥主桥结构形式为（22+106+22） m。该桥的拱轴线下弦杆采用圆弧线与二次抛物线，下弦杆采用二次抛物线，拱顶桁架高度为3.5 m，矢跨比为1/5.5，下拱肋矢高19.27 m，桥宽38 m。顺桥向拱脚处一端设置固定支座，另一端设置滑动支座。该拱桥设计为双向六车道，设计汽车荷载标准为城市-A级，设计车速为60 km/h。该钢桁架拱桥立面布置具体如图1所示。

2 有限元模型的建立

采用Midas Civil有限元软件建立该下承式钢桁架拱桥的三维实桥模型。模型中采用梁单元模拟主纵梁、次纵梁、横梁、桁架拱、风撑等构件，采用板单元模拟桥面板部分，采用桁架单元模拟吊索。实桥模型共有1 600个梁单元，600个板单元，30个桁架单元[5]。具体有限元模型如图2所示。

在实桥模型中拱桥的梁拱连接处采用弹性一般连接，下弦杆各支座处设定为仅绕Y轴转角自由，而上弦杆各支座处则设定为仅Y向位移约束。计算时不同荷载取值大致如下：

（1）恒载：一期恒载包含主梁、拱肋等结构自重;二期恒载取值59.56 kN/m，其中包含桥面铺装、人行道板等。

（2）车辆荷载：汽车荷载设为城市-A级双向六车道荷载;其余均设为人行道均布荷载，取值2.5 kN/m2。

（3）溫载风载：整体升温降温均设为20 ℃;基准风速取25 m/s。

（4）基础沉降：各个支座均考虑5 mm的沉降。

3 主梁刚度对钢桁架静力特性影响分析

主梁刚度的大小关系到钢桁架拱桥整个结构的变形和稳定性[6]。主梁刚度太小，会引起整个结构产生更大的变形，而通过增大截面来增大刚度不仅会增加用钢量，还会加大整个结构的重量，对墩台基础的受力不利。结构刚度主要取决于材料的弹性模量E，为了保持单一变量的原则，本文将主梁的弹性模量E作为结构刚度影响分析的控制变量，以分析主梁刚度EI对结构静力特性的影响[7-8]。

3.1 主梁应力

主梁上缘最大拉应力、下缘最大压应力均出现在下弦杆拱脚处;下缘最大拉应力出现在主梁跨中处;上缘最大压应力出现在边跨跨中附近。通过改变主梁刚度的大小，拟定主梁刚度由0.5EI增大到2EI，得到在承载能力极限状态下主梁内力的变化规律（如图3所示）。

根据图3可知，随着主梁刚度的增加，主梁上缘、下缘最大拉应力均逐渐增大，且上缘最大拉应力均大于下缘最大拉应力;主梁上缘、下缘最大压应力也随着主梁刚度的增加逐渐增大，但下缘最大压应力均明显大于上缘最大压应力。综合主梁应力变化规律可知，当主梁刚度在一定范围内增大时，钢桁架拱桥的主梁应力随之也逐渐增大，主梁刚度对主梁下缘压应力影响较大。

3.2 拱肋应力

改变主梁刚度的大小，对比分析主梁刚度由0.5EI增大到2EI时，在承载能力极限状态下拱脚截面、拱肋1/8截面、1/4截面、3/8截面、1/2截面应力变化规律。

不同主梁刚度对拱肋上、下弦杆关键截面应力的影响如图4所示。由于拱肋沿纵向与横向均为轴对称，选取其中的一侧为研究对象。

由图4（a）可以看出，随着主梁刚度的增大，拱肋上弦杆拱脚截面、3/8截面、1/2截面处的应力逐渐减小，而拱肋上弦杆1/8截面、1/4截面处的应力则逐渐增大，其中上弦杆1/8截面、3/8截面和1/2截面处的应力变化较为明显。根据图4（b）可知，拱肋下弦杆拱脚截面处的应力随着主梁刚度的增大逐渐增大，而拱肋下弦杆1/8截面、1/4截面处的应力随之逐渐减小。当主梁刚度由0.5EI增至EI时，拱肋下弦杆3/8截面和1/2截面处应力呈小幅增大;但当主梁刚度由EI增至2EI时，两截面处应力则呈小幅减小。拱肋下弦杆拱脚截面处的应力受主梁刚度影响较大，其余截面受主梁刚度影响较小。

3.3 主梁变形

主梁在跨中截面出现竖向位移最大值，通过改变主梁刚度的大小，对比分析主梁刚度由0.5EI增大到2EI时，在正常使用极限状态下主梁跨中截面的挠度变化规律。不同主梁刚度对主梁跨中截面变形的影响如图5所示。

由图5可知，随着主梁刚度的增大，主梁跨中截面处的竖向位移逐渐减小。其中当主梁刚度为0.5EI时，主梁跨中截面位移约为11.7 cm;当主梁刚度增至EI时，主梁跨中截面位移减至10.1 cm左右，位移减幅达13.7%;当主梁刚度增至2EI时，主梁跨中截面位移减至7.6 cm，减幅达35%。主梁刚度的增大能够降低主梁竖向位移变化。

3.4 拱肋变形

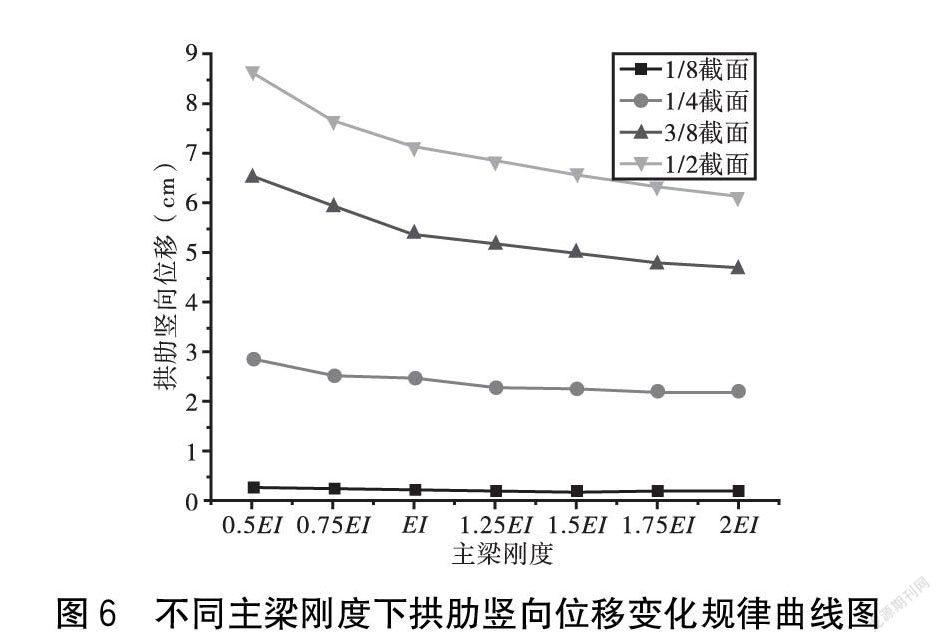
拱肋在上弦杆拱顶截面出现竖向位移最大值，改变主梁刚度的大小，对比分析结构刚度由0.5EI增大到2EI时，在正常使用极限状态下拱肋1/8截面、1/4截面、3/8截面、1/2截面的挠度变化规律。不同主梁刚度对拱肋关键截面变形的影响如图6所示。

由图6可知，随着主梁刚度的增大，拱肋1/8截面、1/4截面、3/8截面、1/2截面处的位移均呈减小变化。其中当主梁刚度由0.5EI增至2EI时，拱肋3/8截面处位移减小了1.82 cm，1/2截面处的位移减小了2.55 cm，说明主梁刚度对拱肋3/8截面、1/2截面处的位移影响较大;而拱肋1/8截面和1/4截面处的位移分别仅减小了0.11 cm、0.66 cm，说明主梁刚度对拱肋1/8截面和1/4截面处位移影响较小。

3.5 吊杆索力

由于吊杆沿纵向与横向均为轴对称，本文选取其中的D1～D8吊杆为研究对象，分析主梁刚度由0.5EI增大到2EI时对吊杆索力的影响情况。不同主梁刚度对吊杆索力的影响如图7所示。由图7可以看出，随着主梁刚度的增大，各吊杆索力均呈逐渐减小变化。在主梁刚度由0.5EI增至2EI时，D1～D8吊杆分别减小了20.8%、19.7%、17.8%、16.2%、14.7%、14.3%、14.3%、14.4%，其中D1～D4吊杆索力减幅较大，表明主梁刚度变化对拱梁相交处附近吊杆索力的影响大于跨中附近的吊杆索力。

4 结语

本文以某下承式钢桁架拱桥为研究对象，模拟研究了不同主梁刚度条件下拱桥静力特性变化规律，得出以下结论：

（1）随着主梁刚度的增大，下承式钢桁架拱桥主梁上緣、下缘的最大拉应力和最大压应力均逐渐增大。

（2）下承式钢桁架拱桥拱肋上弦杆拱脚截面、3/8截面、1/2截面及下弦杆1/8截面、1/4截面处的应力随着主梁刚度的增大逐渐减小;拱肋上弦杆1/8截面、1/4截面及下弦杆拱脚截面处的应力则随之逐渐增大;拱肋上弦杆1/4截面受主梁刚度影响较小，下弦杆拱脚截面受主梁刚度影响较大。

（3）随着主梁刚度的增大，钢桁架拱桥主梁竖向位移逐渐减小，主梁刚度的增大能够有效减小主梁竖向位移。

（4）随着主梁刚度的增大，拱肋各截面处位移及吊杆索力均逐渐减小，主梁刚度对拱梁相交处吊杆索力的影响大于跨中处。

参考文献：

[1]余 浩，阮 杰.纵向预应力对下承式组合桥面系钢桁架拱桥受力性能的影响研究[J].城市道桥与防洪，2020（9）：175-178，22.

[2]郝俊芳，伍 星.某下承式钢桁架拱桥施工控制技术[J].公路，2020，65（11）：188-193.

[3]王占飞，邢宇玥，陈小军，等.上承式钢桁架拱桥抗震性能分析[J].公路交通科技（应用技术版），2016，12（11）：151-153.

[4]葛 亮，王人鹏.钢系杆拱桥的参数研究和设计优化[J].现代交通技术，2017，14（3）：27-29.

[5]税 静.大跨度钢桁架拱桥结构参数影响分析[D].成都：西南交通大学，2017.

[6]曾 迪，刘 斌.矢跨比对中承式钢桁架拱桥静力影响分析[J].湖南交通科技，2018，44（1）：112-114.

[7]袁腾文.吊杆断裂对钢桁架拱桥结构静力影响分析[J].湖南交通科技，2018，44（3）：145-148.

[8]阮 杰.桥面板与钢结构连接方式对钢桁架拱桥受力性能影响分析[J].城市道桥与防洪，2019（11）：49-52，10.

3662501908290