山区桥梁三维空间脉动风场模拟

赵博文

(辽宁省交通运输事业发展中心 沈阳市 110005)

近几年，随着国家脱贫攻坚政策的实施，西部偏远地区交通基础设施建设速度越来越快。由于我国西部地区山地较多，路线经常要穿越高山峡谷地带，沿线建设的桥梁通常跨度较大且距水面或谷底较高，结构刚度相对较柔，对风的作用比较敏感。目前山区桥梁的风振响应已成为控制山区桥梁结构设计和施工的重要因素之一。

桥梁风振响应的分析方法分为频域法和时域法。以前受计算机性能制约，时域法的研究相对较少，但随着计算机技术的发展，时域法的优势已逐渐凸显。桥梁风振响应时域分析首先要模拟空间脉动风场，对三维空间脉动风场进行合理简化，采用MATLAB编制模拟程序，基于谐波合成法(WAWS)，考虑空间相关性，运用FFT技术，对某山区大跨度桥梁三维空间脉动风场进行了模拟。

1 风场的简化

桥梁风工程一般将自然风近似等效为多维多变量的平稳高斯随机过程进行研究。在笛卡尔坐标系下，大跨度桥梁的三维空间风场可表示为[1]：

(1)

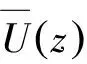
在宽度为桥长、高度为桥塔(桥墩)范围内，将连续风场离散为有限个点的三维风场。实际应用时，忽略三个方向脉动分量间的相关性，仅考虑空间相关性，将具有三维相关性的风场简化为三个独立的一维风场。根据桥梁结构特点，忽略桥塔(桥墩)竖向和主梁顺桥向脉动分量的影响。

2 谐波合成法

目前模拟脉动风速时程的方法主要有三种：线性滤波法、小波变换法和谐波合成法。线性滤波法的优点是效率高，但其并不是无条件收敛的，需要依靠经验选取参数，模拟精度相对较差。小波变换法在模拟非平稳信号时具有一定的优势，但参数的选取和估计对模拟精度有较大的影响，不适合模拟平稳随机过程。谐波合成法是一种利用谱分解和三角级数叠加来模拟随机过程样本的传统方法。因为其理论简单清晰、结果精度较高、适用范围较广，所以在脉动风场模拟中得到了广泛应用。虽然其计算效率不高，但随着计算机技术的发展，这点不足正逐渐被忽略。采用George Deodatis[2]提出的谐波合成法对随机脉动风场进行模拟。

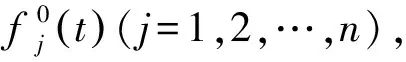
(2)

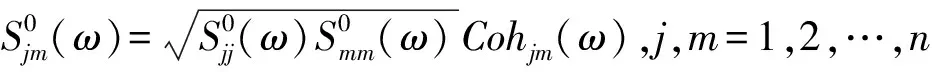
对S0(ω)进行Cholesky分解，可得

S0(ω)=H(ω)HT*(ω)

(3)

其中，T表示矩阵的转置，H(ω)为下三角矩阵。

(4)

式(4)中对角线元素为ω的实非负函数，非对角线元素一般为ω的复函数。

Hjj(ω)=Hjj(-ω),j=1,2,…,n

(5)

(6)

Hjk(ω)=|Hjk(ω)|eiθjk(ω),j>k

(7)

(8)

当N→∞，随机过程的样本可由下式模拟：

(9)

(10)

(11)

(12)

式中：n为模拟点数；N为频率等分点；Δω为频率增量；ωml为双索引频率；φml为均布在[0,2π]间的相互独立的随机相位角；ωu为截止频率；θjm(ωml)为Hjm(ωml)的复角。

模拟的随机过程为周期函数，周期公式如下：

(13)

应用FFT技术，公式(9)可改写成如下形式：

(14)

(15)

(16)

(17)

式中：Δt为时间步长；i为虚数单位；其他符号意义同前文。

时间步长Δt须满足式(18)，等效条件为式(19)：

(18)

M≥2N

(19)

3 脉动风特性参数

表征脉动风特性的主要参数有：紊流强度、紊流积分尺度、紊流功率谱密度和空间相关性。

3.1 紊流强度

风速是一个三维矢量，取平均风速所在方向为x方向，取竖平面内与x垂直的方向为z轴，按右手坐标系，可将风速分解成三个方向上的分量形式。

Vx=U+u(t)

(20)

Vy=v(t)

(21)

Vz=w(t)

(22)

其中，脉动分量u(t)、v(t)、w(t)均被假定为均值为零的随机过程。脉动分量的平均变化幅度用均方差σu、σv、σw表示。紊流强度为脉动分量平均变化幅度和平均风速的比值，分别用Iu、Iv、Iw表示，如式(23)所示。

(23)

我国规范[3]中建议按地表粗糙度类别和高度选取紊流强度Iu的平均值，其余两项分别取Iv=0.88Iu，Iw=0.50Iu。

3.2 紊流积分尺度

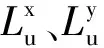
数学上可定义为：

(24)

式中是两个纵向速度分量u1≡u(x1,y1,z1,t)和u2≡u(x1+x,y1,z1,t)的互协方差函数，其他8个紊流积分尺度的定义与其类似。

3.3 紊流功率谱密度

我国规范[3]采用的是沿高度变化的Kaimal谱，其考虑了近地表层中紊流积分尺度随高度发生的变化，表达式如下：

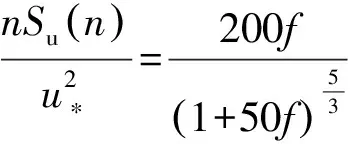
(25)

(26)

(27)

(28)

(29)

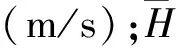
3.4 空间相关性

当空间一点的脉动风速达到最大值时，距其一定距离的另一点脉动风速一般不会达到最大值，且相隔越远，这种可能性越小，这种性质称为空间相关性[5]。对于考虑水平和竖向相关性的结构物，Davenport提出了指数形式的经验公式[4]：

Coh(r,n)=e-f

(30)

(31)

式中：Coh(r,n)为相干函数的平方根；(y1,z1)和(y2,z2)为两点的坐标；n为脉动风频率；U(z1)和U(z2)为两点高度处的平均风速；Cz和Cy为指数衰减系数，由于其取值与地形粗糙度、离地高度和风速有关，缺乏资料时，建议值分别为Cz=10和Cy=16。

4 风场模拟

4.1 计算模型基本数据和分析点位的选取

选取的某山区高墩大跨桥梁包括一座刚构桥和一座连续梁桥，全桥长469.6m，桥墩高19～103m。具体风场模拟点的布置情况见图1。

图1 模拟点布置情况示意图

因山区大跨度桥梁桥址区域的风环境非常复杂，借鉴参考文献[6-7]的研究成果，桥址区域地表类别采用B类地表。基本风速采用规范中某地百年重现期基本风速27.6m/s。为更真实地模拟桥址区域风环境，采用参考文献[8]中桥址区域风参数数值模拟方法对本次计算模型的风环境进行了数值模拟，取得了各模拟点最不利工况下的平均风速。由于风场模拟点的数量众多，只提取主梁典型模拟点进行研究分析。具体提取的模拟点情况见表1。

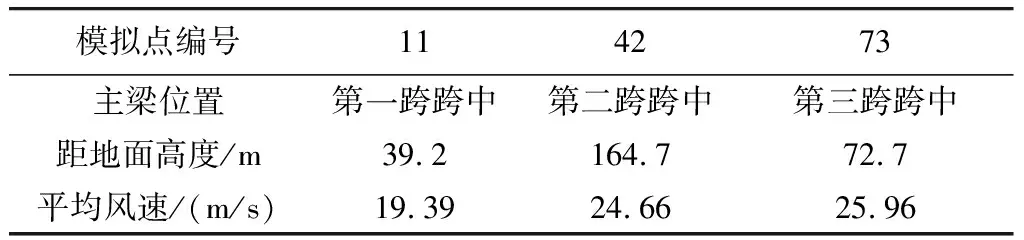
表1 主梁提取模拟点情况

4.2 主梁风场模拟结果

4.2.1功率谱检验

图2 主梁42点横桥向自功率谱

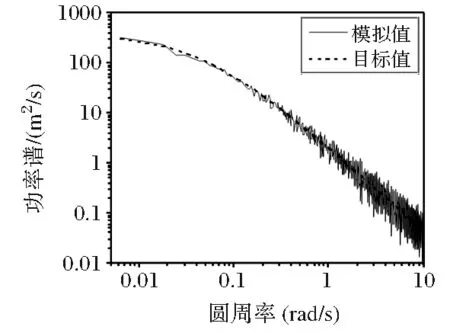
图3 主梁73点横桥向自功率谱

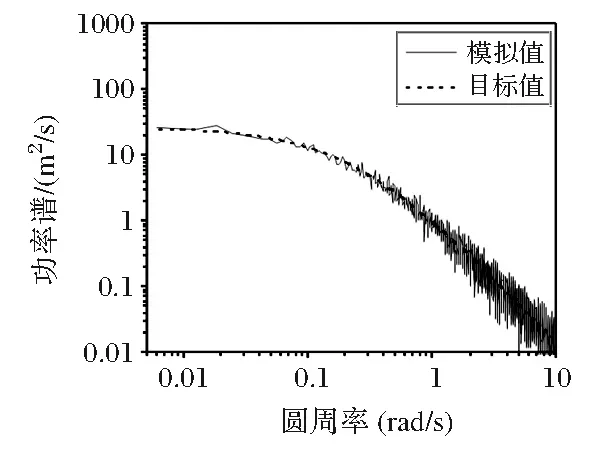
图4 主梁42点竖桥向自功率谱

由图2～图5可见，主梁横桥向和竖桥向的脉动风速功率谱模拟值与目标值吻合较好。

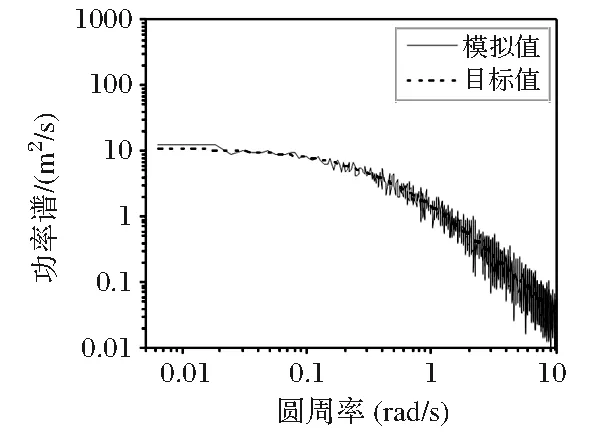
图5 主梁73点竖桥向自功率谱

4.2.2相关性检验

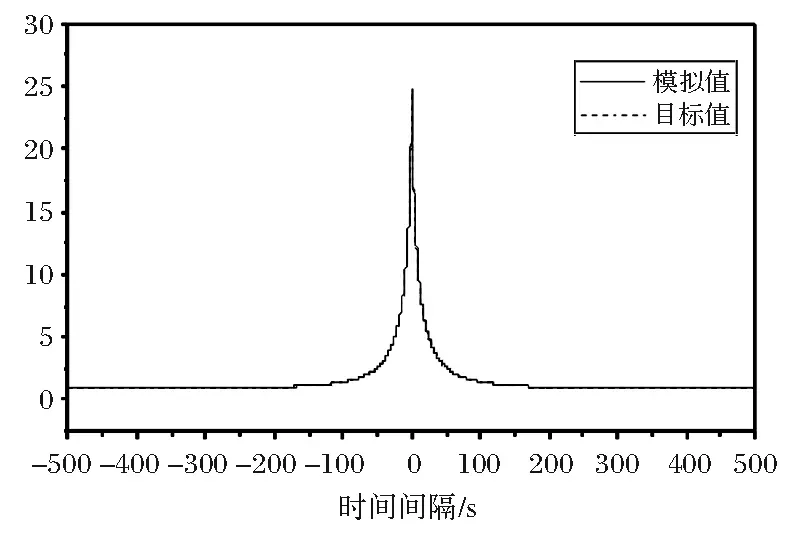
图6 主梁11点横桥向自相关函数

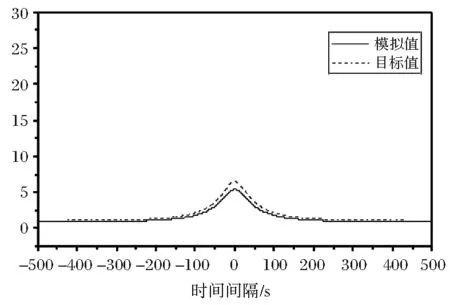
图7 主梁73、11点横桥向互相关函数

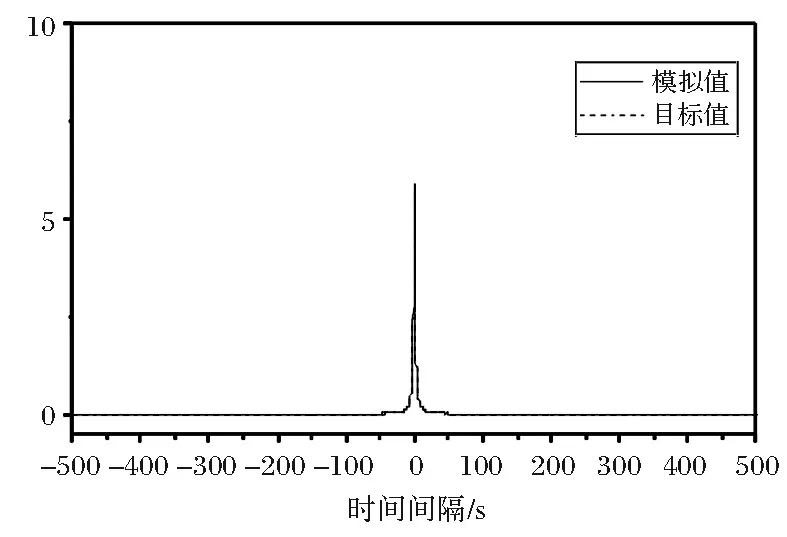
图8 主梁11点竖桥向自相关函数

由图6～图9可见，主梁横桥向和竖桥向的相关函数模拟值与目标值吻合较好。

图9 主梁73、11点竖桥向互相关函数

4.2.3风速时程样本

规范中规定的风时距为10min，提取了73号模拟点横桥向和竖桥向风速时程的前1000s的风速时程片段，见图10、图11。

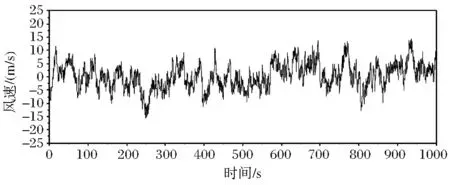
图10 主梁73点横桥向脉动风速时程

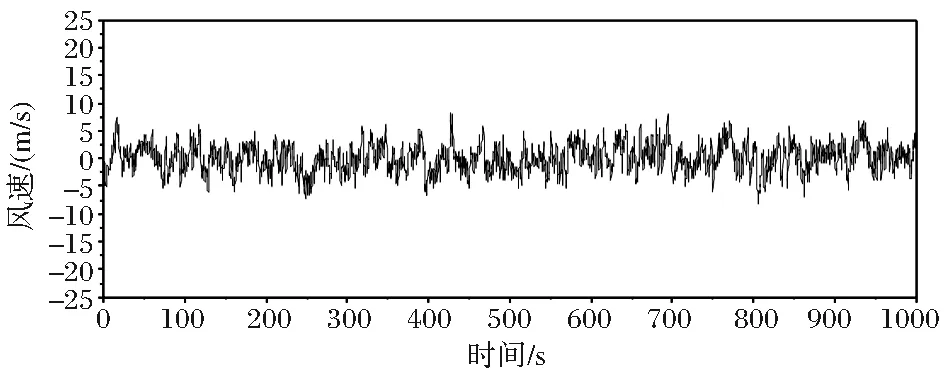
图11 主梁73点竖桥向脉动风速时程

5 结论

首先采用基于谐波合成法的三维空间脉动风场模拟方法，考虑空间相关性并运用快速傅里叶变换(FFT)技术，运用MATLAB编制了风场模拟程序；其次根据桥址区域风环境数值模拟结果，将原始参数带入模拟程序中，计算生成了风速时程样本，并对模拟数据结果进行了功率谱和相关性检验。结果表明运用本文方法模拟的风环境参数，其模拟值与目标值吻合较好。此方法可以满足工程实际应用需求，能够解决山区桥梁三维空间脉动风场的模拟问题。