基于压缩感知的正交偶极子阵列信号参数估计
王炜彤,杨健,郭晓冉,刘鲁涛
1 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001
2 先进船舶通信与信息技术工业和信息化部重点实验室, 黑龙江 哈尔滨 150001
3 北京遥感设备研究所, 北京 100854
4 中国人民解放军32181部队, 河北 石家庄 050000
0 引 言
阵列信号处理主要是利用信号的空域特性来增强信号及有效提取信号空域信息[1-2]。极化敏感阵列本质上是一种矢量天线阵列[3-4],它不仅可以利用信号源的空域信息,还能够获取信号源的极化域信息,这种多维参数的获取能力为提高阵列信号处理的整体性能奠定了物理基础[5-6]。然而,增加的信息量也导致了运算复杂度和硬件成本的提高。根据文献[7]可知,全电磁矢量传感器由3个电偶极子和3个磁环共点正交而成,其能够感知完整的电磁矢量信息。而在实际应用中,为降低硬件和计算的复杂度,可以去除全电磁矢量传感器中的某些电磁感应单元,得到残缺的低维电磁矢量天线,例如,三极子天线和由同点配置且相互正交的一对偶极子天线所组成的正交偶极子阵列。近年来,针对基于偶极子组成的极化敏感阵列的研究备受关注,其中囊括了由若干个极化选择特性不尽相同的天线单元组成的极化敏感阵列[8]。文献[9]提出了基于正交偶极子L形阵列的二维波达方向(direction of arrival, DOA)和极化参数联合估计方法,并采用降维多重信号分类(multiple signal classification,MUSIC)算法显著降低了计算复杂度。文献[10]通过交叉偶极子组成的稀疏平面阵有效实现了信号的二维DOA估计,在保证估计精度的条件下,兼具了低互耦的优势。
传统的信号处理过程中除需要解决信号多维参数的获取问题外,通常还需要面临奈奎斯特采样(Nyquist sampling)定律的限制。而压缩感知(也称压缩采样)(compressive sensing, CS)技术使得低于奈奎斯特采样速率的信号恢复成为可能,故也逐渐被应用于DOA估计和许多相关系统中[11-12]。基于压缩感知技术的DOA估计结构可以在保证估计精度的同时降低系统复杂度,所以具备节约硬件成本的优点。压缩感知的核心思想就是通过在接收信号处理前端链路系统中插入组合网络,引入一个用于线性运算的压缩感知矩阵,以此压缩待处理数据的维度,从而降低系统复杂度和硬件成本。其中,压缩矩阵中的各项通常是从独立同分布(independently identically distribution)的参数中随机选取的。因此,为了尽可能避免维度压缩带来的信息损失,文献[12-15]提到了利用多种方法优化压缩矩阵。近年来,压缩感知技术在单比特量化[16]、调制宽带转换器[17]和多输入多输出(multiple-input multiple-output, MIMO)雷达[18]中得到了广泛应用。
然而,不论是由何种极化选择特性的天线组成的极化敏感阵列,在使接收信息多元化的同时,也会导致接收数据的维度复杂化,这无疑增加了很多运算量。现有的理论研究大多是利用降维方法(例如MUSIC算法[19]及相关优化算法[20])将DOA参数与极化参数进行剥离处理,这种方法在标量信号处理中展现出了较好的估计性能。
针对矢量阵列信号处理领域的问题,本文将提出一种可压缩的正交偶极子阵列结构模型,基于此模型,分析估计降维参数的方法。该方法的核心原理是在天线输出端插入由移相器和累加器组成的组合网络来压缩接收信号的维度,利用降维的MUSIC算法对信号参数进行联合估计,以进一步降低算法复杂度,实现高精度的DOA和极化参数的估计。最后,通过仿真实验对本文所提方法进行验证。
1 阵列模型
1.1 极化敏感阵列接收模型
如图1所示,考虑分布于y轴上的L阵元均匀线阵,阵元为内部分量均指向所在坐标轴正方向的正交偶极子阵列(由十字交叉粗线表示)。图中,θ和φ分别为信号方位角及俯仰角,L表示阵元数量,l=1,2,···,L。
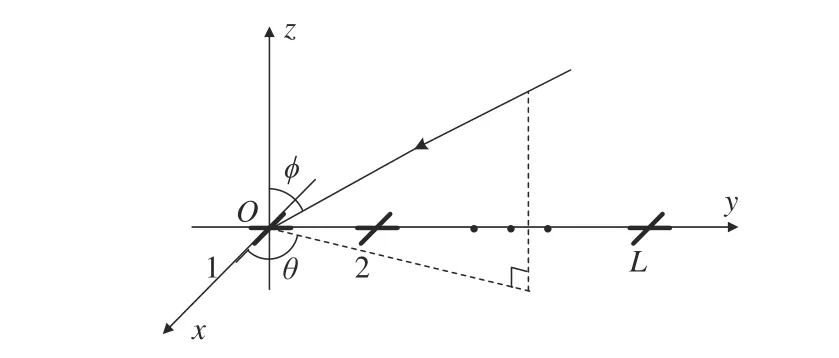
图1 正交偶极子均匀线阵Fig.1 Orthogonal dipole uniform linear array
假设存在K个远场入射窄带完全极化的信号由箭头方向入射,令第k个入射信号的DOA分别为θk和φk(其中,θk为信号方 位角,φk为信号俯仰角),极化参数(极化辅助角和极化相位差)分别为γk∈[0,π/2]和ηk∈[0,2π]。为便于分析和推导,假设入射信号与均匀线阵同在yOz平面内。令阵元噪声均为高斯白噪声,且与各入射信号均统计独立,令Lo=2L,表示接收数据矢量维度,其中下标o代表正交矢量矩阵,则接收数据矢量x(t)表示为
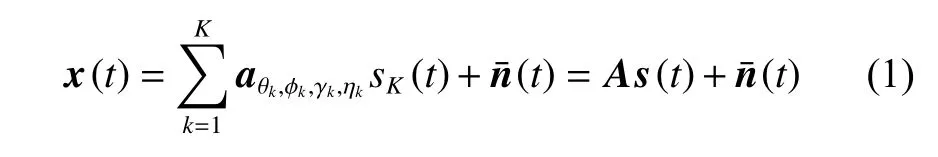
式中:sK(t)表 示K个信号 的 复 包 络;s(t)为发射信

式中: [·]T表示向量转置;uk,l为 第l个阵元处的第k个入射信号的空间相位因子;d为阵元间距;λ为入射信号波长;hγk,ηk为信号的极化矢量,且
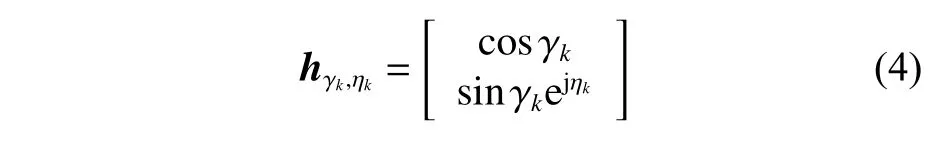
当传感器阵元为正交偶极子时,矩阵 Ξθk,φk表示为
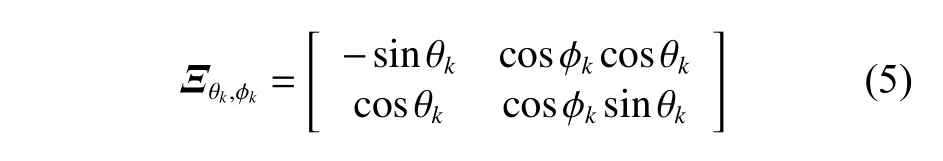
式(5)矩阵中,各项元素只与每个信号的DOA有关,与物理阵元的位置无关。
1.2 基于压缩感知的极化敏感阵列接收模型
本文提出的压缩阵列结构是在空间域中应用压缩感知思想,将阵元数较多的阵列压缩或转换成通道数少得多的阵列,从而可以极大地降低硬件的复杂度(即减少前端链路数量)和软件复杂度(即降低DOA估计算法中的计算量),同时仍保持较高的估计性能。如图2所示,表示L维(微波通道数)的信号矢量[z1(t),z2(t),···,zL(t)]经过组合网络后被压缩为M维(压缩通道数)的信号矢量[z˜1(t),z˜2(t),···,z˜M(t)],φ11,···,φML分 别 为 压 缩 过 程中产生的相移。
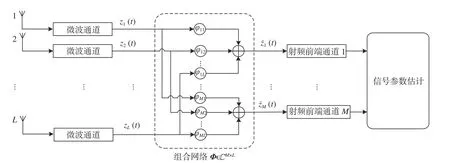
图2 数据压缩结构示意图Fig.2 Schematic diagram of data compression structure
利用数据压缩结构的模型实现方法如下:
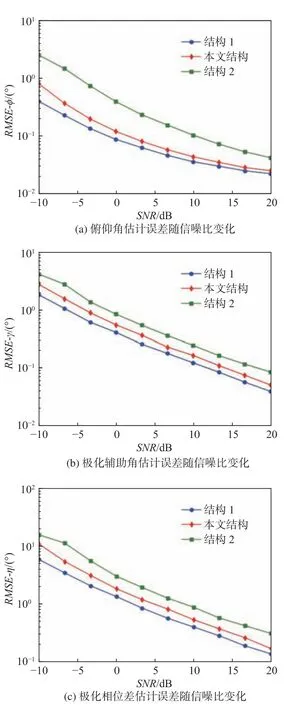
在极化敏感阵列接收部分的射频前端插入一个组合模块,对Lo维的接收信号矢量进行维度压缩,令前端链路压缩通道数为M,且满足M 定义压缩感知矩阵 Φ∈CM×Lo,用于表征组合模块的压缩性能, CM×Lo表 示矩阵维度为M×Lo。因Φ将同时作用于接收信号的信号分量和噪声分量,故假设Φ满足行正交矩阵的条件,即ΦΦH=IM, ( [·]H代 表矩阵的共轭转置,IM表 示M×M的单位阵),以避免噪声子空间扩散到信号子空间[21],并进一步假设压缩过程中未引入额外噪声。值得注意的是,这种数据压缩操作会导致费希尔信息矩阵(Fisher information matrix, FIM)损失,当接收阵列为均匀线阵时,这种信息损失可以用(L−M)/L来量化。为了尽可能避免此类信息的丢失,文献[13-14]提出采用多种基于均匀接收阵列的压缩矩阵进行优化设计的理论和思想,但因本文旨在提出的是基于压缩感知的正交偶极子阵列结构,并研究基于此结构的DOA及极化参数估计方法,故对于上述理论和思想在此不作赘述。图3所示为本文提出的基于压缩感知的极化敏感阵列结构示意图。 图3 基于压缩感知的正交偶极子阵列结构示意图Fig.3 Schematic diagram of data compression based on orthogonal dipole array structure 图3中,K个完全极化信号分别由s1(t),s2(t),···,sK(t)表示,L个正交偶极子阵元的接收信号分别表示为x1(t),x2(t),···,xLo(t),则y1(t),y2(t),···,yM(t)表示经过压缩后得到的M个通道的信号。如图3所示,当正交偶极子分别指向x,y轴正方向时,对于摆放在y轴上的正交偶极子均匀线阵,其阵列接收模型可以表示如下: 式中:n(t)=Φn¯(t),为压缩后的噪声矩阵。经维度压缩后的M维阵列输出协方差矩阵Ryy可以表示为: 式中:Rss为 信号协方差矩阵;σ2n为噪声方差;IL为L维单位阵。 在实际应用中,需要计算阵列的样本协方差矩阵如下: 式中,y(t)为 独立快拍数T下的样本信号矢量,当T趋近于∞时,R˜yy与Ryy的误差趋近于0。 对阵列输出协方差矩阵进行特征分解,得到 式中:Λs和 Λn分 别为对角线元素为K个大特征值和M−K个小特征值的对角阵;与之对应,Us和Un为由特征值和小特征值对应的特征矢量分别张成的子空间(即Us为 信号子空间,Un为噪声子空间)。已知,Us与接收信号的导向矢量张成的空间可视为同一空间,而Un与信号子空间相互正交。利用子空间的正交特性,则有 为便于表示与计算,令DΦHUnUΦDθk,φk≜H(θk,φk), 进一步简化表示为Hθk,φk,从而推导出存在如下关系: 将极化MUSIC空间谱表示为 由此,可得到极化信号的DOA估计值。 由式(9)所示关系发现,可以通过解决以下优化问题实现信号的极化参数估计。 根据2.1节所述,因已完成信号的DOA估计,则对极化参数的估计问题可转化为求解固定的 θ和φ , 即能够使目标函数J(θ,φ,γ,η)达到最小值的γ和η分别为多少。进一步地,由式(3)可知hHγ,ηhγ,η=1, 则上述问题又可化简为在hhγ,η=1条件约束下MUSIC谱函数的最小值对应的点,即求解hHγ,ηH(θ,φ)hγ,η的最小值。最终,上述问题被归纳为一个约束最优化的问题。下面利用拉格朗日乘数法降维。 首先,构造如下代价函数: 由此可见,在hhγ,η=1的 约束下,hH(θ,φ)hγ,η的最小值应为 min(λ) ,当λ为H(θ,φ)的最小广义特征值 然时后,h,γ,η令 则 矩为 阵λ对束应P的θ,φ广={义H特(θ,征φ)向,D量。Dθ,φ},则 对于已得到的DOA估计值,J(θ,φ,γ,η)的条件最小值为Pθ,φ的最小广义特征值,即存在如下关系: 式中, ςmin(·) 和 ς↔min分别为矩阵束的最小广义特征值及其所对应的广义特征向量。根据信号极化矢量定义,结合式(16),可得信号极化参数的确定公式如下: 由式(18)和式(19)不难发现,尽管引入了极化信息γ和η,但在信号参数的估计过程中仍然通过降维方法避免了高维度的空间谱搜索,并进一步减少了运算量。 为便于计算和阵列结构的对比分析,本节选取10阵元(L=10)的正交偶极子阵列为接收阵列,接收数据矢量维数Lo=2L=20。其中,阵元间距d=λ/2 ,压缩通道数M=12。仿真中的信噪比SNR=10 dB,独立快拍数T=1 000。 鉴于线阵列无法进行二维信号参数的估计,故不失一般性地将信号方位角设置为 θk=π/2,如此,可将信号DOA限制在yOz平面上。在设置空间中有6个远场非相干完全极化的入射信号,令各信号俯仰角φk、极化辅助角γk和极化相位差ηk分 别在 [10◦,50◦], [15◦,75◦]和 [30◦,300◦]范 围 内 均匀分布,极化MUSIC空间谱的谱峰搜索以 0.05◦为步进。信号谱峰的搜索结果和极化参数估计结果分别如图4(a)和图4 (b)所示。 由图4可知,对于非相干的极化信号,本文所提出的结构和算法可以给出正确的信号参数估计结果,且空间谱谱峰尖锐。 图4 信号参数联合估计结果Fig.4 Joint estimation results of signal parameters 为进一步分析所提出结构的估计精度,将其与其他结构进行对比。设置对比阵列: 1) 将前文中设置的L=10的正交偶极子均匀线阵,Lo=2L=20 ,压缩通道数M=12,记为本文所提结构; 2) 将L=10 的 正交偶极子均匀线阵,Lo=2L=20,不经过维度压缩,记为结构1; 3)将L=6 的正交偶极子均匀线阵,Lo=2L=12,不经过维度压缩,记为结构2。 以上两种对比结构除均不经过维度压缩外,其他仿真条件与3.1节一致。经过200次蒙特卡罗方法的实验,得到如图5所示信号参数估计的均方根误差随信噪比变化的曲线。 图5 信号参数估计性能随信噪比变化Fig.5 Variation of performance estimation of signal parameters with SNR 在快拍数保持恒定的情况下,随着信噪比的增加,对于俯仰角φk、极化辅助角γk及 极化相位差ηk的估计误差均呈现越来越小的趋势,即估计性能随着信噪比的增加而提高。估计精度最高的阵列结构是结构1,因为它在图中3种阵列结构中拥有最多的通道数,同时也意味着其计算复杂度最高。虽然结构1和本文所提结构都具有10个正交偶极子阵列,但是,压缩感知技术的应用在降低了接收数据维度的同时,也不可避免地造成部分信息的丢失,从而在一定程度上导致了估计性能的下降。然而,当通道数同为6时,本文所提结构的估计精度要明显高于结构2,且在信噪比高于10 dB时,俯仰角的估计均方根误差低于0.05°。这证明了在尽量降低计算复杂度的条件下,本文所提结构确实具有较好的估计性能。 本文提出了一种基于压缩感知的正交偶极子极化敏感阵列结构,基于所构建的结构模型,通过降维MUSIC算法,成功实现了对极化信号DOA和极化参数的联合估计。通过仿真实验对比,结果表明,在通道数相同的条件下,相比于未经压缩的正交偶极子均匀线阵结构,本文所提结构能够获得更高的参数估计精度。对于物理阵元数相同的阵列结构而言,本文所提结构利用了压缩感知技术,使得通道数更少,故以牺牲一定估计精度为代价获得了更低的运算复杂度。
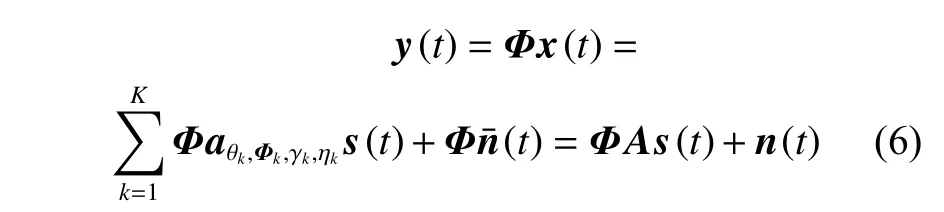
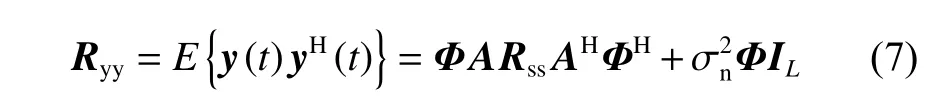
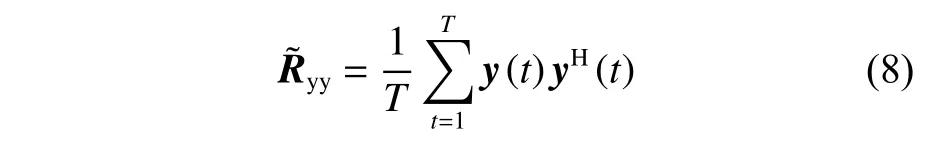
2 降维MUSIC算法
2.1 信号DOA估计
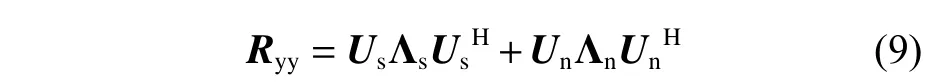
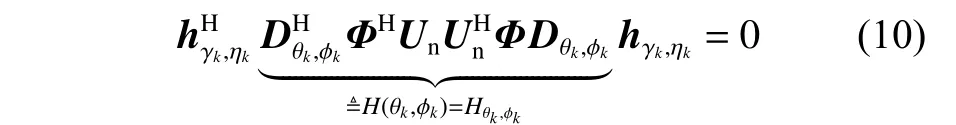
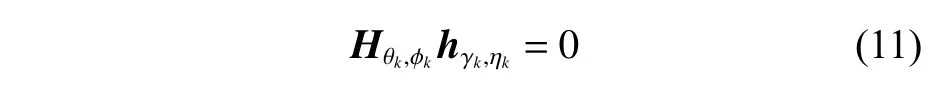
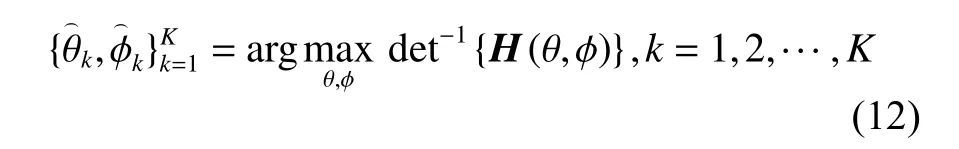
2.2 极化参数估计
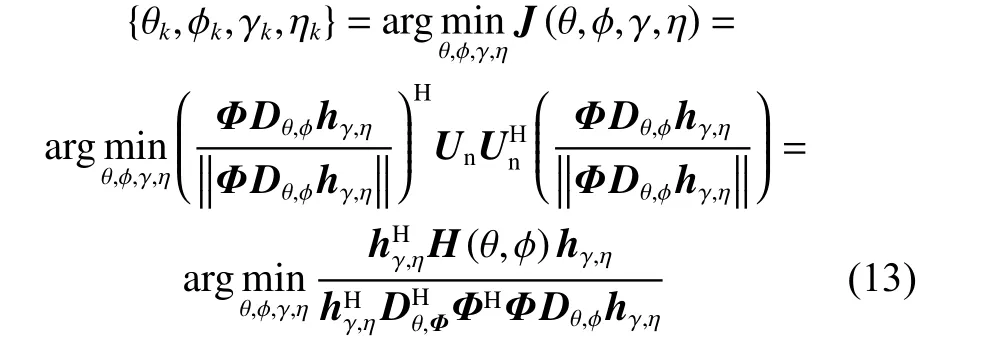
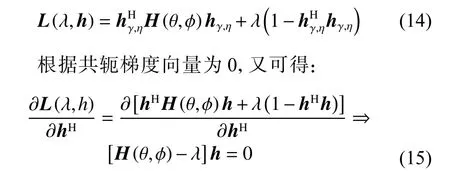
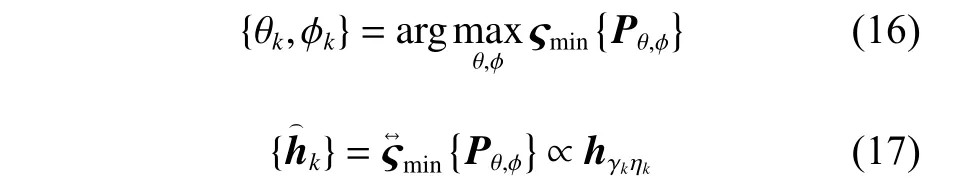
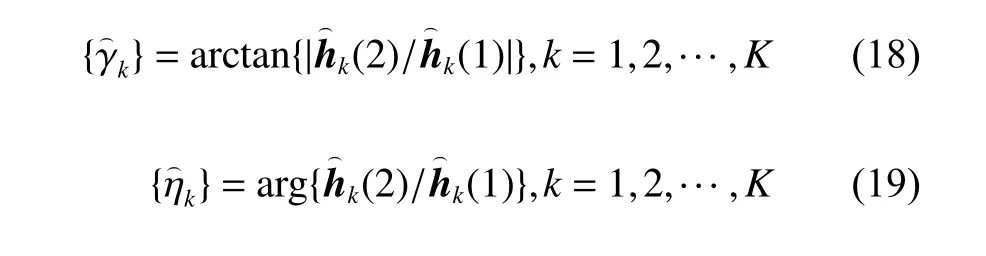
3 算法仿真与分析
3.1 信号参数估计

3.2 均方根误差(RMSE)
4 结 语

