图说数学教育理论的融通




【摘 要】 研究中外数学教育理论之间的融会贯通,可以更好地把握它们的实质,指导数学教育实践,提升中国数学教育研究的理论自信.借助图形分析以下数学教育理论的融通:中国“变式教学理论”与瑞典“变异学习理论”的融通、外来HPM与本土MM教育方式的融通、美国MPCK与中国“四个理解”的融通、美国MKT与中国“数学教学基本功”的融通,倡导透过现象看本质,搞好自己的数学教育,探索符合中国国情的数学教育理论之路.
【关键词】 图说;数学教育;理论融通;理论自信
《数学写真集(第1季)——无需语言的证明》一书由许多“无需语言的证明”的图形组成,书中许多“证明”——图形令人拍案叫绝,充分显示了:“有什么比用插图来展现一个个重要的数学知识点更好的主意呢?”[1]受此启发,笔者希望借助图形直观地理解许多复杂、深奥的数学教育理论,以及它们之间的融会贯通,帮助读者把握其实质,从而更好地指导自己的数学教育实践,并提升中国数学教育研究的理论自信.
关于中外数学教育理论的“融通”研究(“融通”取《现代汉语词典》中“融会贯通”之义),我国著名数学教育家张奠宙(1933—2018)先生率先垂范,在《人民教育》撰文简述中国数学教育的六个特征,并与国外的有关提法相对照(见表1),借以显示中国数学教育的特色[2].他还指导几位数学教育方向的博士构建中国“教育数学”的理论框架,并与美国MKT理论进行对照,认为两者在基本思想上是一致的[3].本文循沿张奠宙先生足迹,继续探讨中外数学教育理论的融通.
1 中国“变式教学理论”与瑞典“变异学习理论”的融通
“变式教学”是我国广大教师普遍接受和使用的教学方法.“变式教学”的起源无从可考,但文献记载20世纪上半叶苏联心理学者针对几何教学中的“标准图形”提出了“变式图形”,并就两者之间的利弊展开了研究和争论.“变式图形”的概念在20世纪60年代传入我国,中科院心理所卢仲衡等学者随即在几何教学中开展研究,鉴于“标准图形”的负面作用以及“变式图形”的优势,他们将“变式”列为数学教学的基本策略之一,即教师通过在教学中变换数学问题的非本质特征,引导学生理解数学概念的本质特征[4-6].
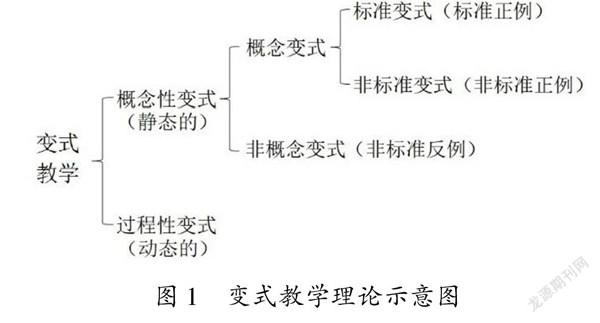
1977年起,顾泠沅先生主持的上海青浦实验研究团队在教学中对学生进行“变式训练”,取得了良好的效果,从而将“组织变式训练”作为他们总结的教学结构中的一个环节.经过持续多年的研究之后,顾泠沅、鲍建生等学者于2003年正式总结了中国“变式教学理论”,被张奠宙先生誉为兼具中国特色和国际水平的数学学习与教学理论.“变式教学理论”的主要观点是:数学教学过程中,一方面要通过直观、具体的概念标准变式(即标准正例)引入数学概念,且通过概念非标准变式(即非标准正例)突出数学概念的本质属性,并通过非概念变式(即非标准反例)明确数学概念的外延,从而帮助学生理解数学概念;另一方面要通过组织有层次的数学活动(即过程变式),引导学生分步解决问题,从而帮助学生积累数学活动经验[7-9].笔者将其概括为图1:
“变异理论”是瑞典教育家马飞龙(Ference Marton)教授创立的学习理论.它发端于20世纪70年代马飞龙等学者提出的现象图析学.20世纪90年代,马飞龙在现象图析学基础上提出变异理论的基本假设:学习就是对事物的某种属性进行鉴别,只有当该属性与其他属性在变与不变中形成对照,这种属性才可能被鉴别和理解,所以经验变异是学习不可缺少的,没有变异就没有学习.后经过对学校课堂中概念教学的实证研究,马飞龙进一步证实经验变异与鉴别关键属性之间的因果关系,提出“变异学习理论”的基本策略——系统运用变与不变,将四种变异范式(分离、类合、对比、融合)与学习内容相结合,明确变异维度,构成学习空间.
2001年,中国“变式教学理论”的总结者顾泠沅与瑞典“变异学习理论”的创立者马飞龙在香港大学相遇,彼此认同对方的理论,并展开合作.比如2002年,马飞龙受邀在上海作了题为《从变异理论看国际比较中数学教与学的差异》[10]的报告,对中国数学教学的特色进行分析并给予肯定.又如2005年,顾泠沅和马飞龙等人联合撰文《变式教学:促进有效的数学学习的中国方式》[11],进一步阐释两种理论的特点.
这充分说明中国的“变式教学理论”与瑞典的“变异学习理论”是融通的,概括起来体现在以下几个方面:
一是研究目的的融通.两者的研究目的都是促进学生的学习,特别是关于概念的学习.虽然“变式教学理论”的出发点是教师的教,但落脚点还是学生的学.
二是核心观点和核心概念的融通.两者的核心观点是学习材料和情境的有序变异对于有效理解学习对象的本质特征至关重要.两者的核心概念“变式”“变异”的英文为同一个词variation.
三是研究方法的融通.两者都注重实践探索与实证研究.“变式教学理论”的形成经历了“变式图形—变式策略—变式练习—变式理论”的长期实践过程,并以获得的大量实验数据作为实证支撑.“变异学习理论”先通过质性分析明确研究对象和基本假设,再通过课堂教学的相关性分析和改善教学的干预性实验验证假设,最终形成基本理论框架,其各发展阶段也都探索、积累了扎实的实践成果[12].
2 外来HPM与本土MM教育方式的融通
20世纪70年代初,国际数学教育委员会(ICMI)专门成立了数学史与教学关系国际领导小组,HPM成为一个正式的数学教育研究领域.HPM是History and Pedagogy of Mathematics(数学史与数学教育)的简称,就是利用数学史来促进数学教育.20世纪末,HPM传入我国.经过20多年的发展,中国的HPM研究已经十分成熟,既有HPM的学术组织、研究团队、理论创造[13],又有HPM的实践队伍、课例模式、案例成果[14-15].
20世纪80年代末,在我国著名数学家徐利治先生倡導的“数学方法论”[16]影响之下,我国中小学层面诞生了MM教育方式.MM是Mathematical Methodology的简称,是指运用数学本身的思想方法指导数学教学及其改革的数学教育方式.经过30年的发展,MM教育方式也形成了自己的学术组织、研究团队、理论创造以及丰硕的实践成果[17].
笔者曾探讨了外来的HPM与本土的MM教育方式在基本立场、研究内容、教学设计与实施方法、促进教师专业发展、理论框架模式(图2)与研究方法等方面的耦合,取得了两者融通研究的初步成果,这里不再赘述.我们从中得到的启示是,无论何种数学教育方式都不能脱离“数学”这个核心、不能脱离“培养学生的数学(核心)素养”这个基本立场.这正是HPM与MM教育方式两者生命力长久之所在,其成果之花才会持续绽放.中国对HPM的贡献、对MM教育方式的创建,增强了中国数学教育研究的理论自信[18].
3 美国MPCK与中国“四个理解”的融通
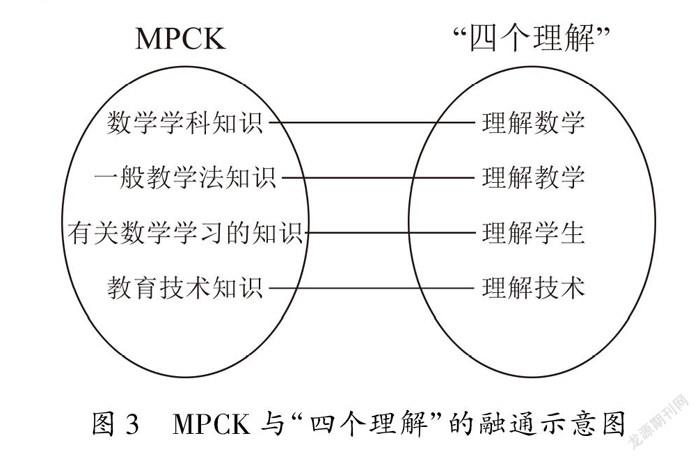
20世纪80年代,美国学者舒尔曼(Shulman)提出PCK理论.PCK是Pedagogical Content Knowledge(面向教学的知识)的简称[19-20],这是关于教师知识的一种理论.PCK提出后受到国外学者重视,并于2005年左右引起我国教育研究者的关注.若结合数学学科来剖析PCK,即为数学教学内容知识(Mathematical Pedagogical Content Knowledge,简称MPCK).MPCK理论认为,数学教师应该掌握四个方面的知识,即:数学学科知识、一般教学法知识、有关数学学习的知识、教育技术知识[21].
2010年,我国人教社章建跃博士提出了“三个理解”的观点,认为理解数学、理解教学、理解学生是课程改革对数学教师提出的新要求,“三个理解”是课程改革的基石,这是实践基础之上的理论概括[22].不久之后,章建跃博士又将“三个理解”扩展为“四个理解”,即:理解数学、理解教学、理解学生、理解技术.“四个理解”的观点受到我国许多中学数学教师的青睐(中国知网收录的以“四个理解”为标题的数学教育文章多达上百篇).
不难发现,作为数学教师专业发展理论,美国的MPCK理论与中国的“四个理解”观点是融通的,具体如图3所示:
相比而言,MPCK理论侧重知识的静态陈列;而“四个理解”侧重知识的动态理解,包括知识的产生、发展、应用等.
4 美国MKT与中国“数学教学基本功”的融通
2000年前后,美国密歇根州立大学教育学院德博拉·鲍尔(Deborah Ball)教授团队也提出了一个关于数学教师知识的理论——MKT,它是Mathematical Knowledge for Teaching的简称,意思是“面向教学的数学知识”.MKT理论认为教师的数学知识包括6个板块:一般内容知识、专门内容知识、水平内容知识、内容与学生知识、内容与教学知识、课程与内容知识.MKT理论建立在MPCK理论基础之上,但更加突出教学实践所需的数学知识,提出之后即受到全球数学教育研究者的青睐[23-24].鲍尔教授也因此获得2017年国际数学教育大奖——克莱因奖.
长期以来,在我国中小学数学教研组中,传承着一条宝贵经验:数学教师应加强教学基本功的训练与提升.这条经验受到我国中小学数学教师以及教育主管部门的广泛重视.根据一项问卷调查获得的数学教学基本功主要包括9个方面:解题、教材解读、新授课教学设计、课件制作、课堂组织、板书、作业设计、复习课与试卷讲评和命题[25].
美国的MKT理论与中国的数学教学基本功经验之间可以对应起来、互相融通,具体如图4所示:
可以看出,MKT理论按照数学与教学两个维度将数学教师的知识进行分类,是一种陳述性的知识分类方法;而“数学教学基本功”经验则按照教学流程分类,是一种程序性的知识分类.两者可以相互转化.
另外,需要指出两点:
一是MKT理论中数学维度的三个知识板块(一般内容知识、专门内容知识、水平内容知识),又与我国传统教育理论中知识的三个层面(知其然、知其所以然、知何由以知其所以然,简称“三知”)是融通的,具体如图5所示:
二是数学教师除了需要上述MPCK、MKT知识,除了做好“四个理解”、提升“数学教学基本功”,还需具备其他一些重要知识,才能既教书、又育人,正如2017年版高中数学课程标准指出的:“数学教师应以《中学教师专业标准》为指导,提升自身的专业水平,数学教师要努力提升通识素养、数学专业素养、数学教育理论素养、教学实践能力.”[26]
以上对中国“变式教学理论”与瑞典“变异学习理论”、外来HPM与本土MM教育方式、美国MPCK与中国“四个理解”、美国MKT与中国“数学教学基本功”等几组中外数学教育理论分别开展了融通研究,旨在建立不同数学教育理论之间的联系,帮助广大教师透过现象看本质,对数学教育理论既不盲目崇拜,也不盲目自信,从而提升教学定力.
参考文献
[1][美]尼尔森.数学写真集(第1季):无需语言的证明[M].肖占魁,徐沙凤,译.北京:机械工业出版社,2014.
[2]张奠宙.关于中国数学教育的特色——与国际上相应概念的对照[J].人民教育,2010(02):36-38.
[3]程靖,马文杰,张奠宙.“教育数学”的内涵及其分析框架研究[J].教育科学研究,2016(06):44-49.
[4]卢仲衡.关于平面几何“标准图形”教学的消极作用的问题[J].心理学报,1961(02):88-100.
[5]卢仲衡.初二学生学习数学所产生的一些错误的分析[J].数学通报,1961(07):29-34.
[6]卢仲衡,茅于燕,应玉叶,马佶为,张梅玲.教学改革中促进学生掌握数学知识的一些心理因素[J].心理学报,1961(3):190-201.
[7]鲍建生,黄荣金,易凌峰,顾泠沅.变式教学研究[J].数学教学,2003(01):11-12.
[8]鲍建生,黄荣金,易凌峰,顾泠沅.变式教学研究(续)[J].数学教学,2003(02):6-10.
[9]鲍建生,黄荣金,易凌峰,顾泠沅.变式教学研究(再续)[J].数学教学,2003(03):6-12.
[10]Ference Marton.从变异理论看国际比较中数学教与学的差异[J].上海教育科研,2002(08):4-9.
[11]顾泠沅,黄荣金,Ference Marton.变式教学:促进有效的数学学习的中国方式[A].范良火,等.华人如何学数学[M].南京:江苏凤凰教育出版社,2017:247-273.
[12]陈红兵.变式理论与变异理论——两个教学理论的比较与关系探析[J].教育科学研究,2016(06):44-49.
[13]汪晓勤.HPM:数学史与数学教育[M].北京:科学出版社,2017.
[14]汪晓勤,栗小妮.数学史与初中数学教学——理论、实践与案例[M].上海:华东师范大学出版社,2019.
[15]汪晓勤,沈中宇.数学史与高中数学教学——理论、实践与案例[M].上海:华东师范大学出版社,2020.
[16]徐利治.数学方法论选讲[M].武汉:华中工学院出版社,1983.
[17]陈江辉.MM方式三十年数学贯通丛书[M].南京:江苏凤凰教育出版社,2019.
[18]刘祖希,陈飞.HPM与MM教育方式的耦合初探[J].数学通报,2020(11):31-34.
[19]Shulman L S. Those Who Understand: Knowledge Growth in Teaching [J]. Educational Research,1986,15(2):4-14.
[20]Shulman L S. Knowledge and Teaching: Foundations of the New Reform [J]. Harvard Educational Review,1987,57(1):1-22.
[21] 李渺,宁连华.数学教学内容知识(MPCK)的构成成分、表现形式及其意义[J].数学教育学报,2011(02):10-14.
[22]章建跃.中学数学课改的十大论题[J].中学数学教学参考,2010(07):2-5.
[23]庞雅丽.美国MKT研究的缘起、发展及启示[J].外国中小学教育,2013(06):36-40.
[24]黄友初.美国的教师教学知识研究——以MKT理论的发展为例[J].比较教育研究,2015(04):83-89.
[25]任念兵,劉祖希.回归数学学科的教学基本功——兼谈“中学数学教师基本功”网络调查[J].中学数学杂志,2020(6):1-4.
[26]中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:97-99.
作者简介 刘祖希(1980—),男,湖北仙桃人,副编审;新青年数学教师工作室创始人,全国数学科学方法论研究交流中心副秘书长兼学术委员会副主任,中国教育学会青少年创新思维教育分会常务理事,中国数学会数学教育分会会员,主要从事数学教育研究与教师培训,倡导“让数学教育研究更加平易近人”;主编《当代中国数学教育名家访谈》《新青年教师文库(数学卷)》《高中数学名师工作室丛书》《高中数学素养养成手册》等著作,发表文章100余篇,担任《数学教学》《中小学课堂教学研究》《青少年科技报》等报刊专栏作者.
3460501908283

