永磁同步电机周期载波调制技术研究∗

李亚伟 顾汝彬 张 琳 何 郑

（1.上海工程技术大学机械与汽车工程学院 上海 201620）（2.中国人民解放军32128部队 济南 250000）（3.华域皮尔博格泵技术有限公司 上海 201999）

1 引言

SVPWM技术凭借其直流电压利用率高和易于数字化控制等优点成为逆变器控制的研究热点。当SVPWM 技术采用固定开关频率调制时，在开关频率及其倍数附近产生边带谐波电压和电流谐波［1］，边带谐波分量会增加电机额外损耗［2~3］并引入电磁振动［4~6］和诱发高频电磁噪声［7~9］，产生严重的电磁干扰［10］。因此，对于SVPWM 逆变器而言，其输出电压谐波含量的幅值和频率是衡量SVPWM逆变电路性能的重要指标之一。

目前SVPWM 技术普遍采用传统三角载波调制［11~12］，其它类型载波研究较少。正弦载波主要在通信领域中使用，用于提高信道利用率和改善系统性能［13］。锯齿载波仅在三相逆变器软开关调制［14］、减少调制波开关次数［15］等方面有少量研究。为了分析三角载波调制、正弦载波调制和锯齿载波调制对于SVPWM 技术影响，选用三角波、正弦波和锯齿波分别作为载波对SVPWM 技术进行调制。基于双重傅立叶级数的相电压谐波分析方法，发现锯齿载波调制的相电压直流电压利用率较高且总谐波畸变最低。根据不同载波调制策略的谐波分量计算结果，提出基于锯齿载波的锯齿波周期频率调制策略，能够有效降低SVPWM 技术调制过程中的边带谐波分量幅值。

2 SVPWM谐波分析方法

国内外学者对于SVPWM 技术产生的边带谐波电压和电流谐波进行了大量研究［16~18］，采用双重傅立叶级数方法研究电压谐波分量，能够准确计算电压谐波分量中各次谐波成分的解析表达式［1，11］，但难以直观看出谐波分布情况和变化规律且求解方法很难直接计算。根据双重傅立叶级数的相电压谐波分析方法，采用数值解法得出不同调制比下电压谐波分量的频率分布情况和谐波幅值大小。该方法简洁直观且易于计算机编程求解，避免了相电压谐波幅值解析表达式的复杂计算，简化了后续谐波计算分析。

为了理解和分析SVPWM 技术引起的边带谐波分量，建立三相电压源逆变电路，如图1 所示。其中2Vdc表示母线电压，Uag、Ubg、Ucg表示三相PWM电压，Uan、Ubn、Ucn表示三相相电压，Uab、Ubc、Uca表示三相线电压，n表示三相负载的中性点，o表示母线地，Uno表示三相负载中性点到母线地之间的电压。

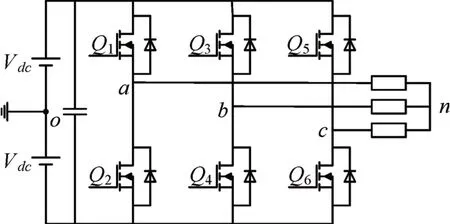
图1 三相电压源逆变器电路

将SVPWM技术中载波信号和基波信号用x（t）和y（t）表示：

其中ωc为载波角频率（rad/s），ωc=2πfc，其中fc为载波频率Hz；θc为载波的初始角度（rad）；ω0为基波角频率（rad/s），且ω0<ωc，ω0=2πf0，f0为基波频率（Hz）；θ0为基波的初始角度（rad）。

根据双重傅里叶级数分析方法，SVPWM 输出的PWM电压可以用下式表示［11］：

式（2）中分别表示输出直流分量、基波以及基带谐波分量、载波频率及其倍数的谐波分量、载波频率及其倍数频率附近的边带谐波分量。

式（2）中Amn和Bmn如下所示：

其中，m表示载波谐波次数，n表示基波谐波次数，则F（x，y）系数可以用复数形式表示为式（5）。

令调制波和载波相交的角度为xf和xr，其中xf表示调制波即将大于载波的相交位置，xr表示调制波即将小于载波的相交位置。根据调制波和载波相交角度为xf和xr，式（5）则可以表示为式（6）。

对于复杂参考波形有多个分段波形组成，因此内积分限写成（xr（i），xf（i）），外积分限写成（ys（i），ye（i）），外部积分不能作为单个连续积分来计算。但可以重新表述为积分段的总和，即

其中j是参考波形中的段数，而ys（i）和ye（i）是段i的开始和结束角度。

认为电机三相负载对称，则abc 三相对电容中点电压对称。故以A相相电压为例分析SVPWM技术调制过程中对相电压的影响，其中A 相相电压Uan和Uao满足以下关系：

三相负载中性点到母线地之间的电压Uno和Uao、Ubo和Uco满足以下关系：

则Uno中仅含有3n次谐波成分［19］和载波频率及其倍数的谐波成分，幅值与Uao中的对应频率的幅值相同。因此，相电压中不含3n次谐波成分和载波频率及其倍数的谐波成分，其余谐波幅值皆与Uao相同。将3n次谐波成分和载波频率及其倍数的谐波成分幅值置零，即可得到相电压Uan各次谐波幅值。

3 载波调制策略分析

SVPWM 技术的PWM 电压占空比函数是由6个等间隔的分断函数组成，其中Vao占空比函数如式（11）所示。

由于SVPWM 技术的6 个分段有6 种不同的表示，则Cmn可以表示如下：

3.1 三角载波调制

为计算Cmn具体数值，需准确计算内积分限值xf和xr，采用三角载波调制的内积分限值xf和xr位置如图2所示。

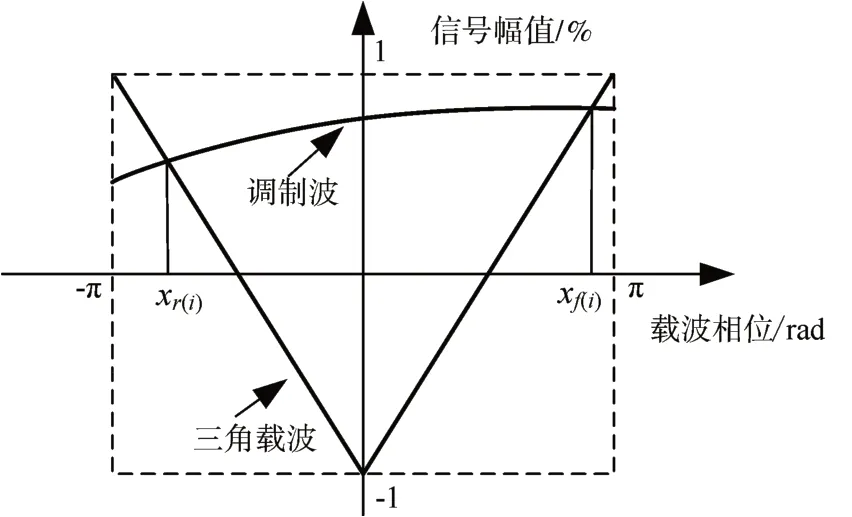
图2 三角载波调制的内积分限值

三角载波函数表达式为

以（2π/3，π）的区间为例，根据式（10）占空比函数段中的表示，则调制波形为

其他区间同理，可得不同函数段的内积分限值xf和xr的计算结果，则基于三角载波调制的SVPWM积分限值的计算结果如表1所示。

表1 三角载波调制的SVPWM积分限值

根据表1 中SVPWM 内外积分的限值，采用数值解法对特定的m和n对Cmn进行求解，将3n次谐波幅值置零和载波频率及其倍数的谐波成分幅值置零，即可得到不同的调制比下相电压Uan各次谐波幅值，计算结果如图3所示。

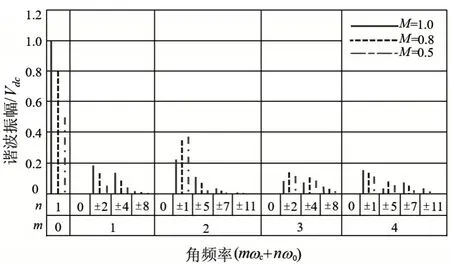
图3 三角载波调制的相电压谐波分布图

为评价在调制过程中相电压的畸变程度，电压总谐波畸变UTHD表示为

Uk表示k次谐波电压幅值；U1表示相电压基波幅值。

结果表明采用三角载波对SVPWM 进行调制且在载波频率1~4 倍范围内调制比M为0.5，0.8 和1时，基波幅值为0.5Vdc、0.8Vdc和Vdc。相电压的电压总谐波畸变分别为120.86%、82.28%和57.87%，谐波电压峰值均位于2倍载波频率边带分量处。

3.2 正弦载波调制

采用正弦载波调制的内积分限值xf和xr位置如图4所示，正弦载波的函数表达式为

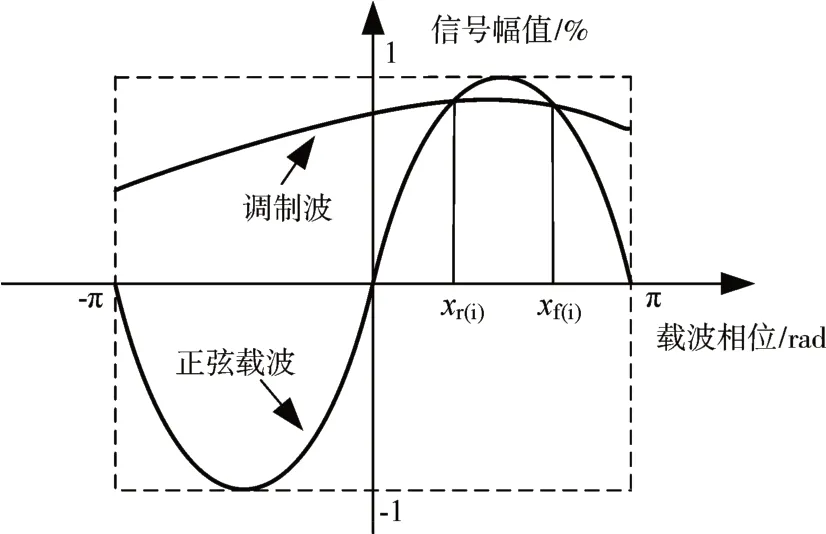
图4 正弦载波调制的内积分限值

同三角载波的计算方式相同，可得基于正弦载波调制的SVPWM 的内外积分限值，计算结果如表2所示。

表2 正弦载波调制的SVPWM积分限值

对Cmn计算可得锯齿载波调制后相电压Uan各次谐波幅值，计算结果如图5所示。

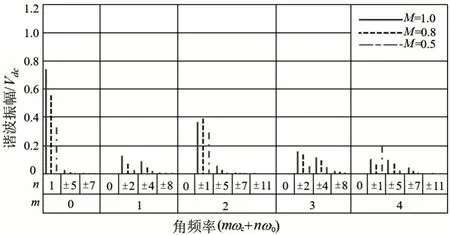
图5 正弦载波调制的相电压谐波分布图

采用正弦载波对SVPWM 技术进行调制，在载波频率1~4 倍范围内调制比M为0.5，0.8 和1 时，基波幅值为0.33Vdc、0.55Vdc和0.75Vdc。相电压的电压总谐波畸变分别为155.69%，112.28%，89.24%，谐波电压峰值位于2倍载波频率边带分量处。

3.3 锯齿载波调制

采用锯齿载波调制的内积分限值xf和xr位置如图6所示。

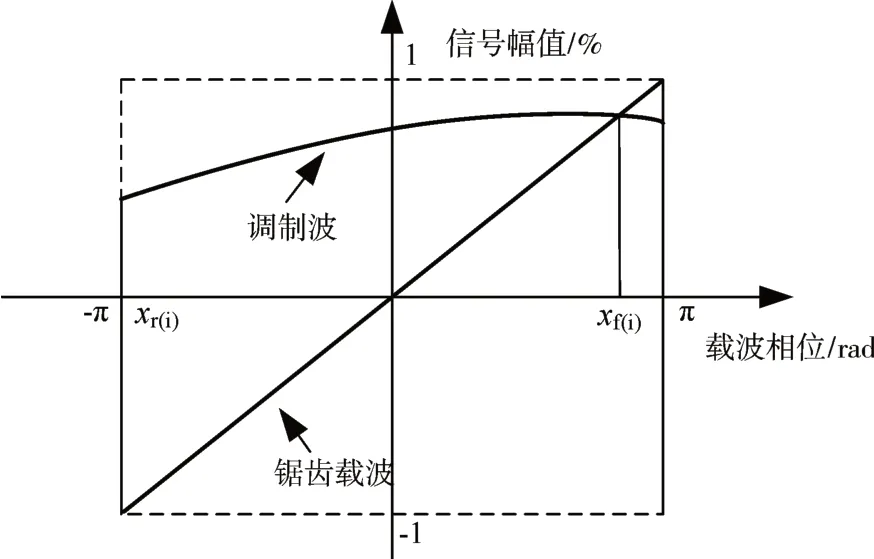
图6 锯齿载波调制内积分限值图

锯齿载波的函数为

同三角载波的计算方式相同，可得基于锯齿载波调制的SVPWM 的内外积分限值，计算结果如表3所示。

表3 基于锯齿载波调制的SVPWM积分限值

对Cmn计算可得锯齿载波调制后相电压Uan各次谐波幅值，计算结果如图7所示。

图7 锯齿载波调制的相电压谐波分布图

采用锯齿载波对SVPWM 技术进行调制，在载波频率1~4 倍范围内调制比M为0.5，0.8 和1 时，基波幅值为0.5Vdc、0.8Vdc和Vdc。相电压的电压总谐波畸变分别为118.16%、72.73%和48.63%，谐波电压峰值位于1倍载波频率边带分量处。

基于不同载波调制的计算结果表明，相电压中均不含三次谐波和载波频率的谐波，三角载波调制和锯齿载波调制均不会产生基频附近的低次谐波，正弦载波调制会产生基频附近的低次谐波。三角载波和正弦载波调制产生的相电压谐波在载波奇数倍频率处仅含有基波偶数倍数的谐波分量，在载波偶数倍频率处仅含有基波奇数倍数的谐波分量；锯齿载波调制产生的谐波中仅含有载波频率处基波奇数倍数的谐波分量。三角载波和锯齿载波比正弦载波的直流侧电压利用率高，且锯齿载波调制的相电压总谐波畸变最低。选用锯齿载波对SVP⁃WM 技术进行调制，在保证直流侧电压利用率较高的基础上，能够降低相电压中的谐波成分。

4 锯齿波周期频率调制策略

根据SVPWM 采用锯齿载波谐波分布特性，选用周期频率调制策略能够有效扩展谐波的分布频率并降低谐波峰值。从周期频率调制扩频的谐波电压峰值和谐波电压频谱分布两方面考虑，锯齿波周期频率调制优于三角波、正弦波和方波周期频率调制［20］。提出基于锯齿载波的锯齿波周期频率调制策略，抑制调制过程中产生的边带谐波分量。

为了分析锯齿波周期频率调制策略对电压边带谐波分量抑制效果，首先采用固定频率的锯齿载波对SVPWM 技术进行调制，利用Matlab/Simulink建立SVPWM 技术的仿真模型，得到其相电压谐波分布情况。仿真模型中，母线电压为100V，电机运行频率为50Hz，载波频率为5kHz，调制比为0.8。采用锯齿载波调制的相电压谐波分布结果如图（8）所示。

结果表明在载波频率1~4 倍范围内，相电压的电压总谐波畸变（THD）的计算结果72.73%和仿真结果72.26%基本一致。谐波最大幅值位于4950Hz和5050Hz处，最大谐波电压的幅值为14.09V。

为降低SVPWM 技术调制过程中谐波电压的幅值，提出基于锯齿载波的锯齿波周期频率调制策略，描述调制信号特性参数主要有调制系数mf和调制率δ。

式中：fc为载波频率，Δfc为fc的最大偏移量；fm为调制函数f（t）频率，f0为逆变器输出信号频率。

在此调制策略中，调制函数的频率fm取值为50Hz，逆变器输出信号频率取值为50Hz，Δfc为fc的最大偏移量取值为1kHz，即表示载波频率在1/50s 内 完 成 从4kHz~6kHz 的 频 率 变 化。 即

在周期频率锯齿载波调制下相电压谐波分布结果如图9 所示，根据图8 和图9 的基波幅值和相电压的电压总畸变进行分析，结果显示此调制策略不影响基波电压的幅值大小且不减少相电压的电压总谐波畸变，仿真结果与帕斯瓦尔（Parseval）定理一致，验证了仿真模型的正确性。根据图8 和图9 的谐波分布频率和幅值大小，表明此调制策略能够明显扩展谐波分布频率，有效降低谐波电压幅值大小，谐波电压最大幅值从14.09V 降低至7.01V，载波频率及其倍数频率处边带谐波分量明显降低，谐波电压频率扩展效果较好。

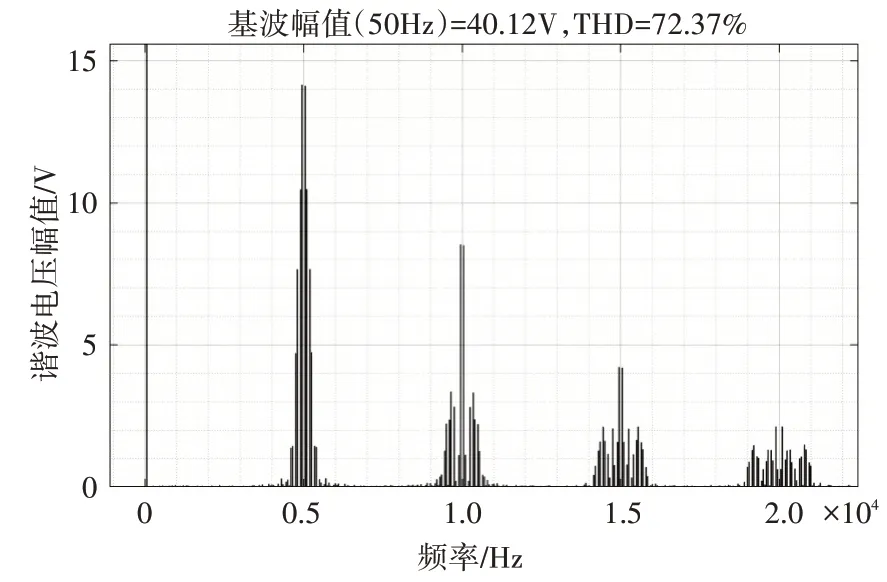
图8 固定频率锯齿载波调制下相电压谐波频谱图

图9 周期频率锯齿载波调制下相电压谐波频谱图

5 结语

为研究不同载波调制对SVPWM 谐波特性的影响，采用三角载波、正线载波和锯齿载波对SVP⁃WM 技术进行调制，采用基于双重傅立叶级数的相电压谐波分析方法对不同载波调制产生的相电压进行计算。结果表明，不同载波调制策略对SVP⁃WM 的相电压谐波影响较大，锯齿载波直流侧电压利用率最高且锯齿载波调制的相电压总谐波畸变最低。为降低调制过程中谐波电压的幅值，提出了基于锯齿载波的锯齿波周期频率调制策略，该策略能够有效降低载波频率及其倍数频率处边带谐波分量，谐波电压最大幅值从14.09 V 降低至7.01 V，谐波电压频率扩展效果较好，能够显著提高SVP⁃WM逆变电路性能。