学习可视化表征工具软件算法设计研究

朱良学

(酒泉职业技术学院，甘肃 酒泉 735000)

0 引言

学习可视化及其表征工具结构导图是提高学生学习兴趣、增强学生自主学习能力的一个重要途径和优秀工具。在知识更新异常迅速的学习型社会，利用可视化技术将抽象的知识转变成为易于被人们接受认知的图形图像，有助于知识快速学习和传播，利用结构导图软件来绘制知识结构导图也成为知识爆炸时代一个必然的选择[1]。与传统媒介(纸笔)相比，单幅图(一个文件)能储存的知识量足够大，知识概括结构性、系统性好，一目了然；易于保存，便于修改，携带、与人交流和传播都非常方便。要绘制出内容丰富、结构清晰的知识结构导图，图中各知识分支(关键词节点)在界面的布局，就是一个核心重要的问题。

因此，基于手绘结构导图的经验和规则，总结出结构导图软件的布局规则，设计出结构导图软件的布局算法，就成了设计结构导图软件的关键问题[2]。

把结构导图中的每个知识分支抽象成一个节点，知识分支间的逻辑关系用有向边表示，这就是一个有向图。结构导图软件的布局问题就转化成为一个有向图的层次布局问题。

1 学习可视化及其表征工具

“可视化”一词，来源于英文的“visualization”，原意是“可看得见的，清楚的呈现”，也可译为“图示化”，如计算机编程的可视化界面(VB,VC等)。学习可视化是指学生在学习过程中运用可视化学习工具将学习内容(知识)、学习过程细节、学习成果以直观形象的视觉方式表征，激发学生学习的积极性、主动性，增强学生的学习兴趣，提高学生的学习效率[3]。利用学习可视化技术将严谨但枯燥的专业学习过程转变为直观、生动形象的个性化学习，极大地提高学生在知识学习中的创新意识和兴趣，最终提升学生自主学习之品质，提高学习绩效。

学习可视化的表征工具，其代表性工具就是思维导图和概念图。本人在研习思维导图应用实践的过程中，发现了博赞思维导图在学生学习应用中的不足和缺点：思维过于发散，思维深度广度不够，思维系统性差；遂提出了结构化思维导图(结构导图)的概念，使思维导图与结构化思维相结合，更好地体现了学习可视化在学生学习中的优势[4]。如图1就是一幅“英语语法知识体系”典型结构导图。

图1 “英语语法知识体系”典型结构导图

2 有向无环图

从图1典型的结构导图实例出发，将导图中的每个知识分支简化为图中的一个节点，即导图中有多少个分支，图中就有多少个节点；导图中知识分支间的关联关系用图中节点与节点之间的边表示。这样抽象的图有三个显著特征：

节点位置层次性：节点位置有明显的层次关系；节点之间关系方向性：节点之间的箭头是单指向的，两节点间只能有单向逻辑关系；由于是结构化图，图中不可能存在环[5]。

这样就将结构导图转换为一个有向图。导图中分支与分支间的关联是单向的，这样的图一般是一个有向无环层级图。

有向图(Directed Graph ):图中所有边都是有向边；有向边由图中两个顶点有向连接构成，从一个顶点指向另一个顶点的箭头表示边的方向[6]。

有向无环图(Directed Acyclic Graph，简称DAG): 在图论中，如果一个有向图无法从某个顶点出发经过若干条边回到该点，则这个图是一个有向无环图，如图2.

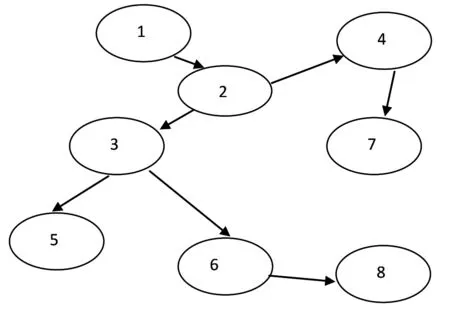
图2 有向无环图

层级图(Hierarchical Graph):指一个已分层的有向无环图，图中所有边都没有方向表示，构成边的两个节点(父节点，子节点)已经含有方向关系[7]。

这样结构导图在平面上的绘制呈现问题就转化为一个有向无环图在平面上的布局问题[8]。

3 Sugiyama层次布局算法

层次布局算法,最典型最常用的是由Sugiyama,Tagawa和Toda(1981)提出的Sugiyama算法[9]。标准的该算法通常由三个部分构成:

第一，分层(Layer Assignment):将图中所有节点分层，同层的节点具有相同的纵坐标；

第二，交叉减少(Crossing Reduetion):对层内节点重新排序，减少边与边的交叉数量；

第三，坐标分配(Coordinate Assignment):计算节点的坐标，同层的节点具有相同的纵坐标。

4 运用Sugiyama层次布局算法进行层次指定

定义1 给定有向无环图(Directed Acyclic Graph,DAG)DAGG=(V,E),V是图G中节点的集合，E是图G中节点之间边的集合。

宽度：对于图G中任一节点v∈V,对应有一个宽度w；

图的分层：将图G的节点集合V分成子集V1,V2,…,Vk, 并且V1,V2,…,Vk互不相交；对于任一边(u,v)∈E,u∈Vi,v∈Vj,则有i>j.如此分层的DAG即为分层图。分层图的层的数目h即为该图的高度。

定义2 层Vk的宽度为w(Vk)﹦∑VEVk,分层图的宽度w﹦max1≤k≤w(Vk).很显然，通过分层，将所有节点归置在不同的层中，假定某图有k层，则表示该分层图的高度为K,其取值范围在1～k.这样图中每个节点都确定了纵坐标，同层的节点纵坐标值相同。

4.1 最长路径分层算法

这种算法思想简洁清晰，容易实现：假定某图为G，u为G中任一节点，又图中根节点所在层设为层1，则u的层数值即为该节点至根节点的最长路径+1.这种算法能够求得层数最小的分层结果，但将会使图的宽度变为最大值。

4.2 最小化宽度分层算法

最长路径分层算法使图的层数最小，宽度变大，这样的布局很不协调。为了找到一种长宽最一致的分层，提出了最小化宽度分层的思想：通过添加虚拟节点将设定部分做下移处理，使层中顶点数目减少，从而使交叉减少。找到一种宽度和高度都最佳的分层本身就是一个鱼或熊掌不可兼得的问题，由于虚构节点也需要占据空间，导致的结果是图的宽度值有可能大于预期值。

4.3 虚拟节点最少化分层算法

该算法目标是要找到一种虚拟节点最少的分层。减少虚拟节点(边)，不仅可大大减少交叉模块花费的时间，而且使得图的布局更加协调、紧凑。但同理，这种算法对于图的长度和宽度没有良好的处理。

基于以上算法的优缺点，在上面三个算法基础上，Healy 和Nikolv于2001年提出了著名的WHS-layering算法：修正了最小化宽度分层算法的宽度边界问题，而且通过参数的设置，可以设定图的宽度和高度边界值，以及调整节点和边(虚构节点)的宽度值。显然，这是一个折中有效的处理结果。

5 运用Sugiyama层次布局算法减少交叉

图的层次布局要简洁、紧凑，简洁就是节点间逻辑关系结构性好，紧凑就是图布局要协调，不能太散。图中边与边的交叉直接影响了图的逻辑性，使图不易阅读。所以，层次布局中要最大可能的尽量减少边与边交叉。减少图中的交叉数量不仅使图的逻辑表达更流畅，表示的内涵也更易于理解。最简单的一个交叉减少思路莫过于：“可减少图中两个输入层之间的交叉数量”设想，这就是2-交叉减少算法[10]。

要对整幅图进行“交叉减少”，一般有K-层交叉减少算法，这一算法的基础就是2-交叉减少算法。下述的“逐层清理”(layer-by-layer sweep)思想也是以2-交叉减少算法为基础，旨在减少整个图的交叉数。

由于每层中节点的排列顺序决定了图中的交叉数目，即便图中仅有两层，，要设计算法完全消除其中的交叉都是不可能的，目前能达到的就是设计有效的算法尽量减少边的交叉数。

下面说明“逐层清理”过程的主要思想。

第一，节点顺序初始化。对每一层各个节点的顺序进行初始化,具体做法就是对节点编号，从左到右依次为1,2,…,n,n为该层的节点数，其中也含虚拟节点在内。

第二，自顶向下清理。设定层Li-1,从i﹦2,…,k, 做循环, 使用一个单边2-交叉减少算法找出层Li的一个新排序。

第三，自底向上清理。设定层Li-1,从i～k开始,反过来第(2)步,使用一个单边2-层交叉减少算法找到层Li的一个新排序。

第四，重复第(2)步和第(3)步,若无法获得更优的结果，终止。

2-层交叉减少算法中一般用的是单边(one-sided)2-层交叉减少算法,其思路比较容易理解：先设定两层中的一层不动,对另一层进行重排，从而减少交叉。基于该思想的常见启发式算法有如下一些：排列启发式算法、重心启发式算法、中值启发式算法、分支切割启发式算法、贪婪交换启发式算法等。

下面着重说明排列启发式算法和重心启发式算法。

排列启发式算法的思路是：先穷尽所有可能性，即将一层中的所有节点进行排列；而后择优，即从所有产生的排列中选择出最小交叉的排列。其优点很明显，能够找到单边2-层交叉减少的最优结果。缺点也很显著，如果这一层中节点数比较大(N个)，当然也包括虚拟节点，那计算量就非常大(N!)，时间复杂度为N!，这就不易用了。

下面通过一个实例来说明重心启发式算法的思路。

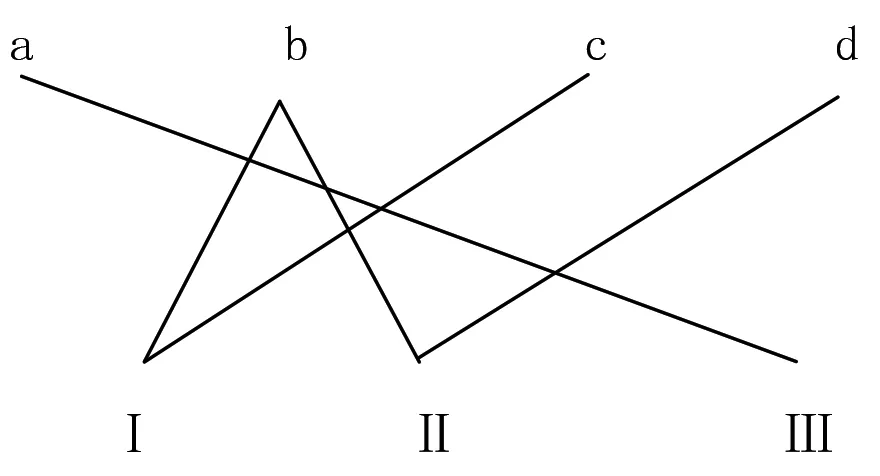
如图3所示，第一层有四个节点a,b,c,d,其初始顺序依次为1,2,3,4；第二层有3个节点Ⅰ，Ⅱ，Ⅲ ，其初始顺序依次为1,2,3；显然，图3的交叉数为5.

现在按照节点相关联的边在邻层中的平均顺序值重排节点。

第一步，先设定abcd所在的第一层不动，与Ⅱ相连接的两边端点为bc，其在第一层的顺序分别是2和3,可以算出X的重心值为2.5.同理，Ⅱ和Ⅲ的重心依次计算得出为3和1.由于第一层(abcd所在层)不动，根据Ⅰ,Ⅱ,Ⅲ的重心值按从小到大排序,得到新的节点顺序为Ⅲ，Ⅰ，Ⅱ.如下图4所示：

图4的交叉数已减少到1.

第二步，再设定Ⅰ,Ⅱ,Ⅲ所在的第二层不动，如上计算出abcd的重心值，得到新的排序为acbd，如图5所示：

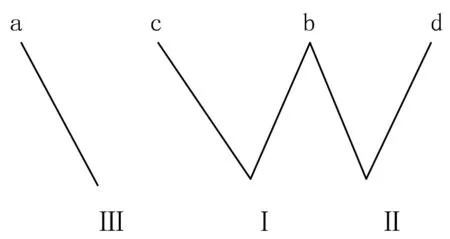
图5 交叉数0

图5的交叉数已减少到0.

由于重心启发式算法思路简洁、易于理解，输出结果表现良好，时间复杂度也呈线性，并不复杂，因此得到广泛应用。

6 运用Sugiyama层次布局算法进行坐标分配

现在要计算分层图中所有节点的坐标，这些节点包括真实节点、虚拟节点(实际是有向无环图中的边)。虚拟节点的引入虽然方便了分层处理，但也产生了多余的弯曲点，要尽量减少。对图中所有节点横坐标(X-坐标)和纵坐标(Y-坐标)可以分别单独进行计算[11]。

纵坐标(Y-坐标)计算的规则是：同一层中的所有节点具有相同的Y-坐标，也就是它们的Y值都一样；Y值通常是由节点所在的高度以及层与层之间的最短距离决定。

X-坐标的计算。对于一个分层图G﹦(VUB,E;L)，V是所有真实节点的集合，集合B表示所有虚拟节点，集合E表示所有边，集合L表示所有层。每层中节点之间的最小距离用Δ表示。分层图的横坐标计算问题就可以做如下描述：

分层图G﹦(VUB,E;L)中每层的节点都已排好序；v和u是G中同层相邻的节点，v∈V∪B，

u∈V∪B；x(u)+Δ≤x(v).

通常横坐标的计算采取的策略有两种：利用启发式算法，不断对布局逐步改进，以期达到目标效果；对一个受约束的坐标差异的目标函数做最优化处理。

式(1)(2)是Sugiyama算法中的目标函数：

(1)

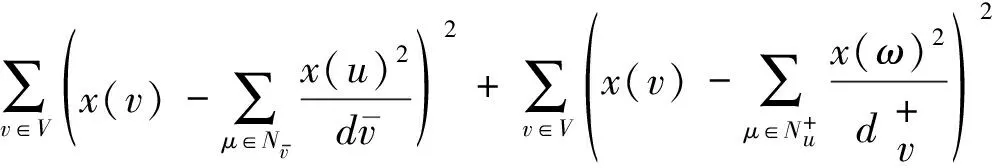
(2)

现在对这两个表达式做分析和说明。u和v是G中同层的两个相邻节点。

1)式主要是判定分层图的边的长度。

2)式作用主要是处理节点与其上、下层相邻节点的位置关系问题，尽量使节点与其上、下层相邻节点保持协调。

显然目标函数受到两个因素的影响，一个是层中节点最小距离Δ，一个是虚拟边的约束。

要控制分层图的边的长度，一个必要条件是：分层图中任何一个节点都位于其相邻节点坐标的中心。用式(3)来计算节点的X坐标：

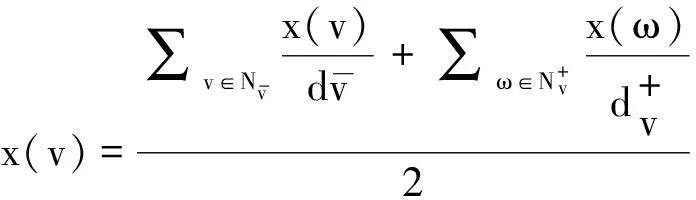
(3)

用这个表达式计算出的节点坐标，不论从图的平面性而言，还是从图节点分布的匀称性而言，布局效果都是良好的。

为了保证分层图布局后的易读性，一般考虑以下三个方面的因素：尽可能使边的长度要短一些，这样使图紧凑; 尽可能使跨层边要保持直；对于图中任何一个节点，其位置要能使该节点与其上下层的相邻节点保持协调、匀称。(1)(2)(3)解决了前两个因素的问题。对于第三个因素，Sugiyama算法的解决策略是这样的：假定对于图G,对于任何一条有向道,v1,…,vk∈V,v2vk-1∈B，用式(4)来做控制：

(4)

7 算法总体设计构想

以上对图的布局所涉及的关键问题及其重要细节做了分析处理,现在给出算法的总体设计思路。遵循解决复杂问题由易到难的简化原则,将一个典型的结构导图剥离其中所表达的内容因素,抽象成有向无环平面图，有向是因为结构导图中一个上一级节点指向下一级节点的关系是单向的,只能是上一级节点指向下一级节点,它们之间是父子关系,图中的有向边表达的其实就是这种关系[12]。再把这一有向无环平面图转换为层级图，层级图中的每条边都没有方向表示,其上下父子关系已经隐含了方向表示，现在问题就转换成一个层级图的平面布局问题。Sugiyama算法是最典型的层级布局算法。运用Sugiyama层次布局算法进行层次指定，将图中所有节点分层，同层的节点具有相同的纵坐标。层次指定相当于层级图布局中节点位置的重新调整，层次越多，图中边与边的交叉就有可能越发增多，节点间逻辑关系就会呈现结构很不清晰的状态，这样就需要运用Sugiyama层次布局算法中另一个模块来减少边与边交叉。由于要完全消除这样的交叉不可能，只能设计算法尽可能减少边的交叉数，使图重新逻辑关系清晰，结构性好。最后需要运用Sugiyama层次布局算法进行坐标分配,对于层级图中的节点要确定其在平面布局中的具体位置。处在同一层中的节点纵坐标相同，这个值通常可以由节点所在的高度以及层与层之间的最短距离计算出来。横坐标的计算稍显复杂，前面已有论述，此不复述。算法整体设计如图6所示：

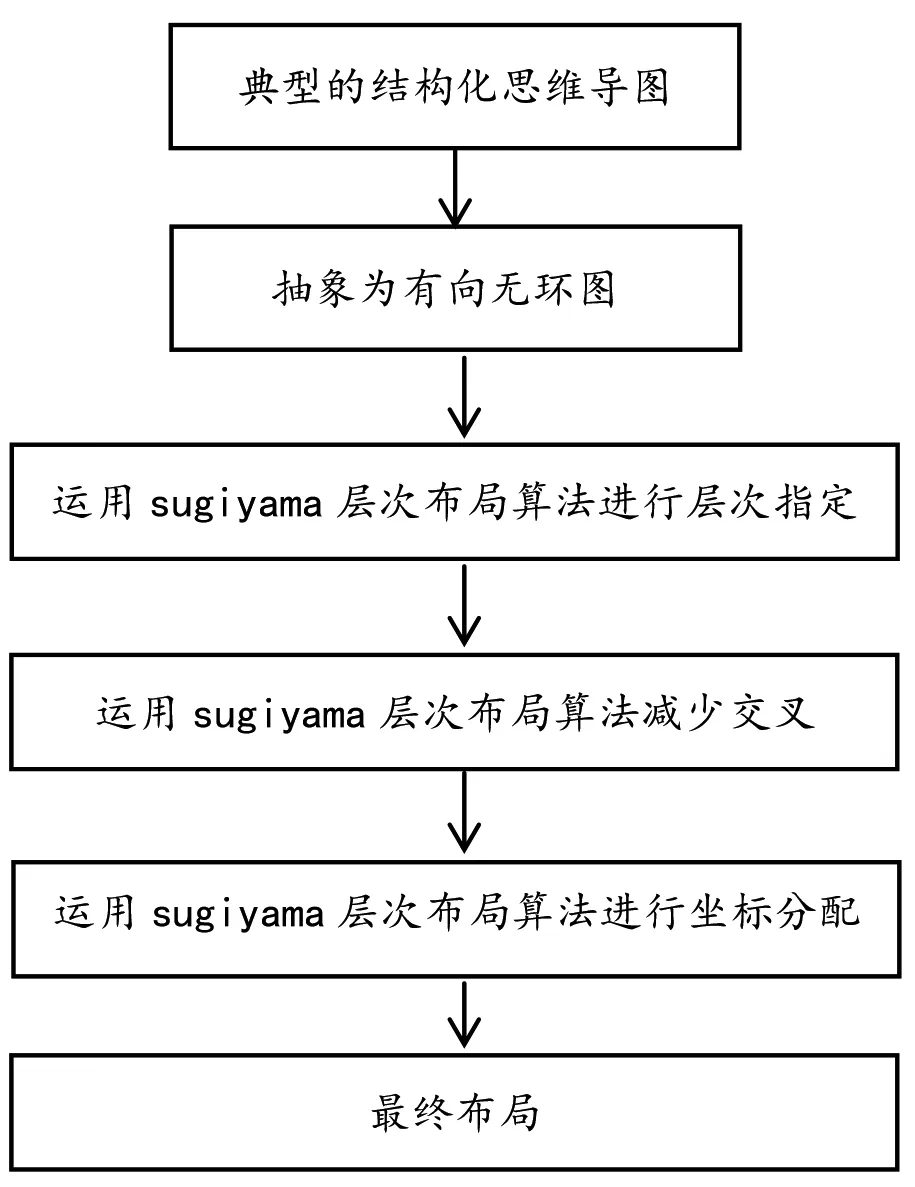
图6 算法整体设计

8 结论

结构导图是学习可视化的一个重要表征工具，在结构导图软件的设计过程中，知识分支节点在平面上位置的调整、分布，即图的布局问题是一个基本而又重要的问题。本文将一个典型结构导图抽象简化为一个有向无环图，应用Sugiyama层次布局算法中的“分层模块”对此有向无环图进行分层，处理了虚拟节点；对分层后的节点应用“减少交叉”模块减少节点间边的交叉数，使节点间逻辑关系结构清晰；应用“坐标分配”模块计算出图中各节点的坐标，同层的节点具有相同的纵坐标，主要是横坐标计算；考虑了图中节点分布的匀称性、可读性好等因素。该算法已在本人申请的甘肃省高等学校科研项目《学习可视化理论、应用及其表征工具软件设计研究》中得到应用，并编程实现，得到了比较理想的效果。