含I 型裂纹八次对称二维准晶动力学问题的数值模拟

王雅楠，李联和，2，王桂霞，2，胡学佳

（1.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

由于具有耐高温及抗氧化的显著特性，准晶热障涂层在发动机等部件中应用广泛［1-2］。发动机热障涂层技术是通过对内燃机内部件喷涂热障涂层使基体金属起到绝热屏蔽作用，从而促进燃料的完全燃烧，减少有害气体的排放及冷却水的消耗［3］。裂纹、孔洞、位错及夹杂等缺陷是影响准晶材料强度的主要原因，因此关于准晶断裂力学问题的研究成为数学、力学以及工程等相关领域科研工作者们关注的焦点。

众所周知，对准晶断裂动力学问题的求解比对静力学问题的求解更困难。带裂纹的准晶静力学问题研究成果较多［4-9］，对于准晶动力学问题，即使增加很多限制条件，仍然很难进行解析求解。选择数值方法进行求解，限制条件少，能更好地模拟实际问题。基于波动—扩散模型［10］，祝爱玉等［11］首次将求解晶体材料问题的有限差分法推广应用到求解准晶弹性动力学问题上，研究了动态应力强度因子随准晶材料常数的变化规律及裂纹动态扩展过程，取得了有意义的数值结果。王晓芳等［12］研究了带Ⅰ型Griffith 裂纹的二十面体Al-Pd-Mn 准晶在冲击载荷作用下的动态响应问题，数值求解了裂纹尖端处应力、位移以及动态应力强度因子，重点分析了相位子场波的传播及扩散情况。王芳［13］用有限差分法求解十次对称准晶中的动力学裂纹扩展问题，采用中心Griffith 裂纹与单边Griffith 裂纹矩形试样考查了裂纹尖端处的位移、应力、应变场变量随时间的变化规律。Sladek［14］基于局部Petrov-Galerkin 无网格方法来解决十边形准晶中的裂纹问题。杨连枝［15］通过将二十面体准晶的弹性边值问题转化为等价变分问题，开发了二十面体准晶的静态弹性有限元算法，给出了具有不同声子—相位子耦合参数二十面体准晶的解析解与数值解。Zhao 等［16］利用广义不连续位移边界积分—微分方程法分析了一维六方热电弹准晶复合材料中一个任意形状的三维界面裂纹问题。马晴等［17］探究了含Ⅱ型单边裂纹的八次对称准晶动力学问题，探讨了板端加载与裂纹面加载对动态应力强度因子的影响。陈曦［18］分析了含Ⅰ型单边裂纹的八次对称准晶动力学问题中不同参数对裂纹尖端处声子场应力强度因子及相位子场位移分量的影响。上述结果表明了有限差分法对求解准晶动力学问题的可行性和有效性。

波动—电报模型［19］更具一般性，利用该模型研究准晶动力学问题才刚刚开始。基于波动—电报模型，Li［20］研究了十次对称准晶动力学问题，分别推导出满足四阶偏微分方程的两个基本解和满足二阶双曲型扩散方程的一个基本解，周建敏等［21］数值求解了带Ⅱ型Griffith 裂纹的十次对称准晶动力学问题。本文将基于波动—电报模型，利用有限差分法对含I 型Griffith 裂纹的八次对称二维准晶动力学问题进行数值模拟。

1 基本方程

1.1 运动方程

假设以z-轴为二维八次对称准晶周期方向，xy-平面为准周期平面，裂纹沿着周期方向穿透整个材料的裂纹表面，即∂/∂z=0。根据准晶弹性理论，有变形几何方程

其中：ui和wi分别代表声子场和相位子场位移；εij和wij分别表示声子场和相位子场应变，x1和x2表示在指标符号系统中的笛卡尔坐标x和y；ui表示uxi；wi，εij以及wij的表示方法与ui类似。及广义Hooke 定律

其中λ，μ为Lame 常数，R为声子场—相位子场耦合常数，ki(i=1，2，3)为弹性常数；σxx，σyy，σxy，σyx表示声子场应力，Hxx，Hyy，Hxy，Hyx表示相位子场应力。把变形几何方程和广义Hooke 定律代入到波动—电报模型

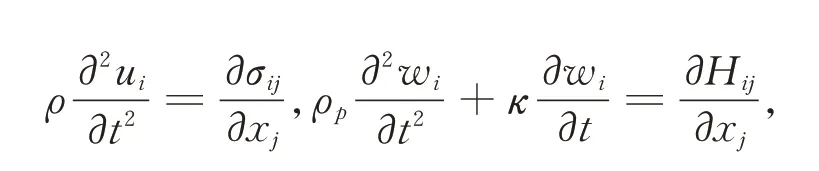
得到波动—电报方程组

1.2 初始条件及边界条件

初始条件为

边界条件

其中P(t)=P0f(t)为动态加载函数，P0是常数，f(t)是Heaviside函数。

1.3 网格划分

空间步长取Δx=Δy=h，时间步长取Δt=τ。首先将求解区域[0，L]×[0，H] 向四周延伸h/2，再对计算区域[-h/2，L+h/2]×[-h/2，H+h/2]进行网格划分，如图1。

图1 网格划分Fig.1 Mesh subdivision

1.4 离散格式

采用中心差分公式对方程组（1）进行离散，有

方程组（2）为方程组（1）的全离散格式。

在边界处，对垂直于边界的偏导数用向前差分或向后差分进行离散，对平行边界的偏导数使用中心差分进行离散。对于角点处使用外推法计算。初始条件的离散类似。

2 误差估计

定理1在计算区域内部，空间步长取Δx=h1，Δy=h2，时间步长取Δt=τ。假设声子场和相位子场的位移存在高阶导数，离散格式（2）的截断误差为

证明由Taylor 展式得

3 稳定性估计

证明使用Fourier 分析法［22-23］对方程组（2）进行稳定性分析，将

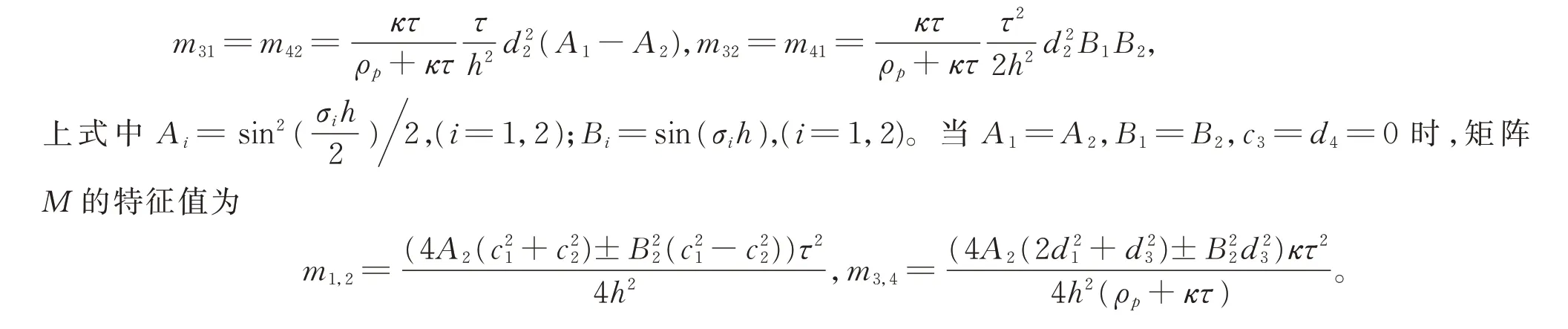
当特征值mi(i=1，2，3，4)＜1 时，即满足

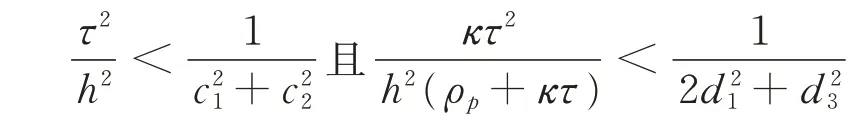
时，方程组（2）是稳定的。

4 数值实例

若无特殊说明取a=2.4 mm，板长L=10 mm，板宽H=25 mm，p0=1 MPa。

由于八次准晶未有实测数据，故取声子场弹性模量c11=2.343×10-1g·mm-1·μs-2，c12=0.574×10-1g·mm-1·μs-2，相位子场弹性模量K1=1.220×10-1g·mm-1·μs-2，K2=0.240×10-1g·mm-1·μs-2，K3=0.200×10-1g·mm-1·μs-2，R=0.01μ，ρ=4.186×10-3g·mm-3。

裂纹尖端和非裂纹尖端（3.7，0.3）处声子场位移和相位子场位移随时间的变化如图2。

图2 位移随时间变化图Fig.2 Displacement versus time diagram

从图2 可以看出声子场位移呈波动趋势，相位子场位移呈扩散趋势。裂纹尖端处位移值较大。但由于对称性，裂纹尖端处y方向位移值为0。

裂纹尖端处声子场和相位子场的应力分量随时间变化如图3。由图3 可以看出，波到达裂纹尖端的时间t0≈3.35 μs，横波的速度c1=≈7.48 mm/μs，波传播速度等于V=≈7.46 mm/μs，约等于横波的速度，这说明声子场中的波传播起主要作用。

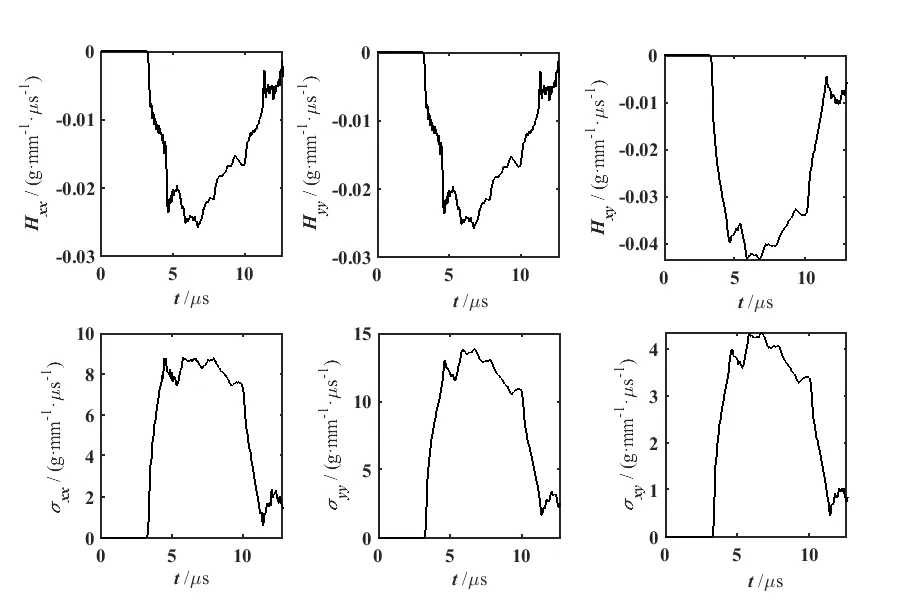
图3 应力分量随时间变化图Fig.3 Stress component versus time chart

选取试样的宽度为25 mm，30 mm，35 mm，声子场动态无量纲应力强度因子如图4。对于Ⅰ型对称准晶，无量纲应力强度因子为，其中

由图4 可以看出，试样宽度H为25 mm，应力波到达裂纹尖端的时间t0≈3.35 μs；试样宽度H为30 mm，应力波到达裂纹尖端的时间t0≈4.01 μs；试样宽度H为35 mm，应力波到达裂纹尖端的时间t0≈4.68 μs，表明试样宽度H越大，应力波到达裂纹面的时间越长。

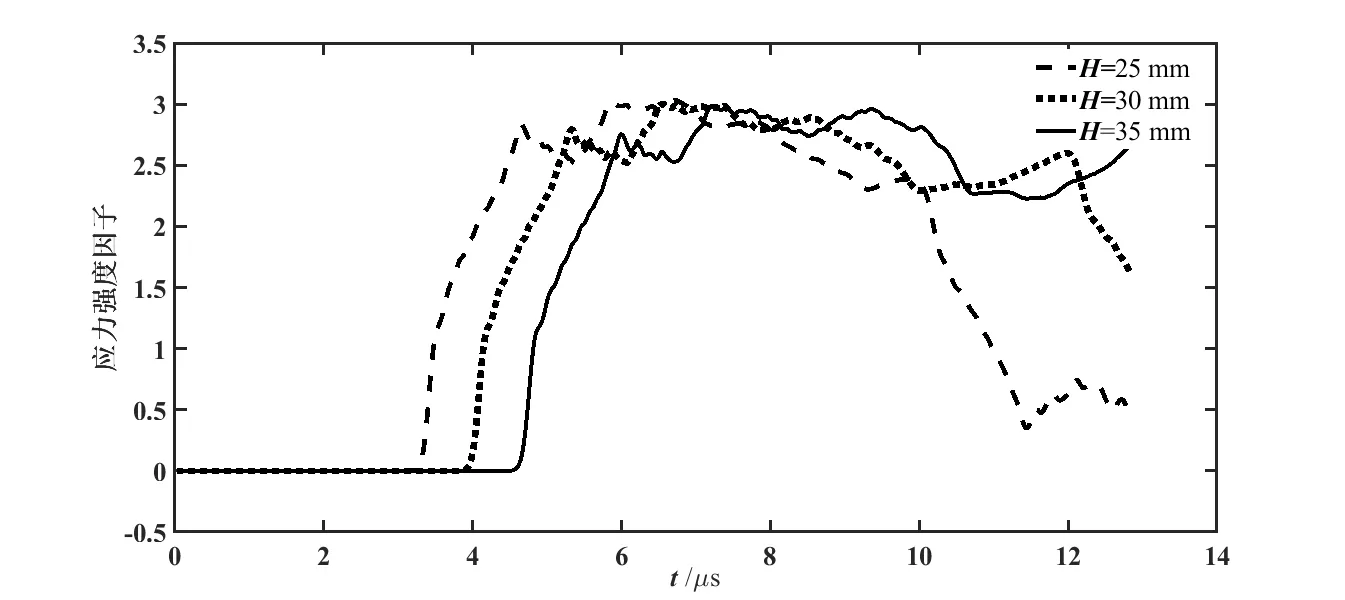
图4 试样宽度H 对无量纲化应力强度因子的影响Fig.4 Effect of specimen width（H）on intensity factor of dimensionless stress

板宽H=20 mm 时，有效质量密度ρp和摩擦系数κ对裂纹尖端处相位子场位移wx的影响如图5。

由图5 可以看出，当摩擦系数远大于有效质量密度时，相位子场波的传播呈指数衰减趋势，摩擦系数对波的传播影响占主导。随着摩擦系数逐渐减小，相位子场波的传播呈指数衰减且出现波动趋势，有效质量密度的改变将会影响相位子场的位移量。

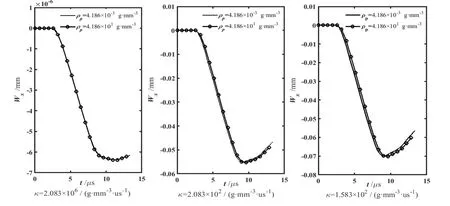
图5 有效质量密度ρp 和摩擦系数κ 对相位子场位移wx 的影响Fig.5 The effect of effective mass density（ρp）and friction coefficient（κ）on the phase field displacement（wx）

5 总结

本文基于波动—电报模型，求解了带Ⅰ型裂纹的八次对称准晶动力学问题，利用有限差分法构造了混合精度的离散格式，该格式的截断误差为利用Fourier 分析法给出稳定条件。数值实例表明：

（1）裂纹尖端处相较于非尖端处位移值较大；

（2）随着板宽H的增加，应力波到达裂纹面所需的时间也在增加；

（3）摩擦系数远大于有效质量密度时，相位子场波的传播呈指数衰减趋势，摩擦系数对波的传播影响占主导，随着摩擦系数逐渐减小，相位子场波的传播呈指数衰减且出现波动趋势，有效质量密度的改变将会影响相位子场的位移量。