钆单晶磁化曲线的微磁学模拟
陈志斌,曹永军
(内蒙古师范大学 物理与电子信息学院,内蒙古 呼和浩特 010022)
钆(Gd)是唯一在室温下具有磁性的稀土元素,是一种典型的海森堡模型铁磁体,也是具有代表性的经典磁制冷铁磁材料[1]。在过去的几十年中,HCP 结构的Gd 得到了广泛关注,大量应用于实验和理论研究,特别是在电子结构和有限温度磁性能方面,Gd 元素的许多基态性质都得到很好解释[2]。基于Landau-Lifshitz(L-L)方程的微磁方法[3],可以求解典型铁磁材料和器件的磁矩运动,但是这些计算中,不能解释在有限温度下的热传导效应,故而引入了一种原子尺度的有效自旋哈密顿量在稀土元素中,由于Gd3+离子的纯s 态性质,导致了相对较低的磁晶各向异性[4],所以Gd 占有突出的地位。针对钆这种对温度很敏感的材料,研究其内部参数与温度的关系是非常重要的。同时,钆是很好的合金元素,在耐热镁合金中,由于钆元素的加入可提高其高温强度和抗蠕变性能[5]。开发含Gd 的合金也是一个重要的研究方向。
因为Gd 具有室温磁性转变点,本文应用混合蒙特卡罗微磁学方法,研究了Gd 单晶在室温附近磁化强度随外场和温度的变化规律,得到磁化曲线。通过Gd 单晶的变化规律可以对不同温度下的Gd 单晶各向异性常数、交换作用系数进行研究。混合蒙特卡罗微磁学方法的应用,对后续类似Gd 单晶的其它铁磁性物质的研究具有指导意义。
1 混合蒙特卡罗微磁学方法
混合蒙特卡罗(HMC)方法是基于经典牛顿力学的运动方程通过积分求解而来的方法,目的是产生exp(-S[x])的类玻尔兹曼(Boltzmann)分布[6]。求解的常规路径是首先设定特定的场景与该场景下的初始状态,根据哈密顿方程产生与时间相关的连续状态,随着状态的不断改变,可以逐步实现平稳态附近的涨落并靠近稳态,但它受限于计算机的计算能力和其他因素,包含“时间”被拆分成离散的序列。这里“时间”可以是真实的时间也可以是虚拟的。
HMC 方法在低温下求解硬磁材料的磁滞回线与L-L 方程的微磁学相近,但对于软磁材料的计算,HMC 方法得到的磁滞回线相较于L-L 方程更为准确[7]。因为L-L 方程在矫顽力附近超过一半的磁矩为反平行亚稳态,而HMC 微磁学由于直接到达能量最小而无此情况。此外,大规模计算方面HMC 微磁学较L-L 方程微磁学快很多,HMC 微磁学在回线计算的每个外场下计算耗时均匀,而L-L 方程在矫顽力附近耗时较多。当微磁学格子数超过1 000 时,HMC 方法计算速度正比于格子数,计算速度远超L-L 微磁学的速度。
1.1 HMC 微磁学算法的迭代过程
1.2 程序中重要参数
参数迭代步数Nstep对HMC 微磁学模拟结果有重要影响。在微磁学领域应用时[9],迭代步数Nstep有所不同。迭代步数Nstep和蒙特卡罗时间δτ两者相互制约,两者的变化影响着HMC 算法的接受率,共同影响着算法的准确性。此外,迭代步数的取值影响着程序运行的时间。
在HMC 算法中,单个轨道中的“蛙跳”的迭代步数Nstep通常是10。对于HMC 的微磁学模型中,单个轨道的“蛙跳”的迭代步数Nstep需要进一步研究,这里设置为200。在HMC 算法中,蒙特卡罗时间通常被分成若干个轨道,每个轨道的长度为τ0=Nstepδτ,轨道数量为Ntrajectory,所以迭代步数取值需要同时兼顾算法的准确性和计算效率。
通过计算得到钆低温下的磁化曲线,先找到钆单晶HCP 密排六方的模型(见图1),其中晶胞参数[10]a=b=363.6 pm,c=578.26 pm,α=β=90°,γ=120°。每个原子有12 个近邻(即Z=12),自旋S=是第一、二个电子归一化的自旋算符。在铁晶体中,由自旋波实验获得的Je/KBTC是0.22,而根据如下方程计算得到的结果是0.093(S=1,Z=8)或0.25(S=1/2,Z=8)。
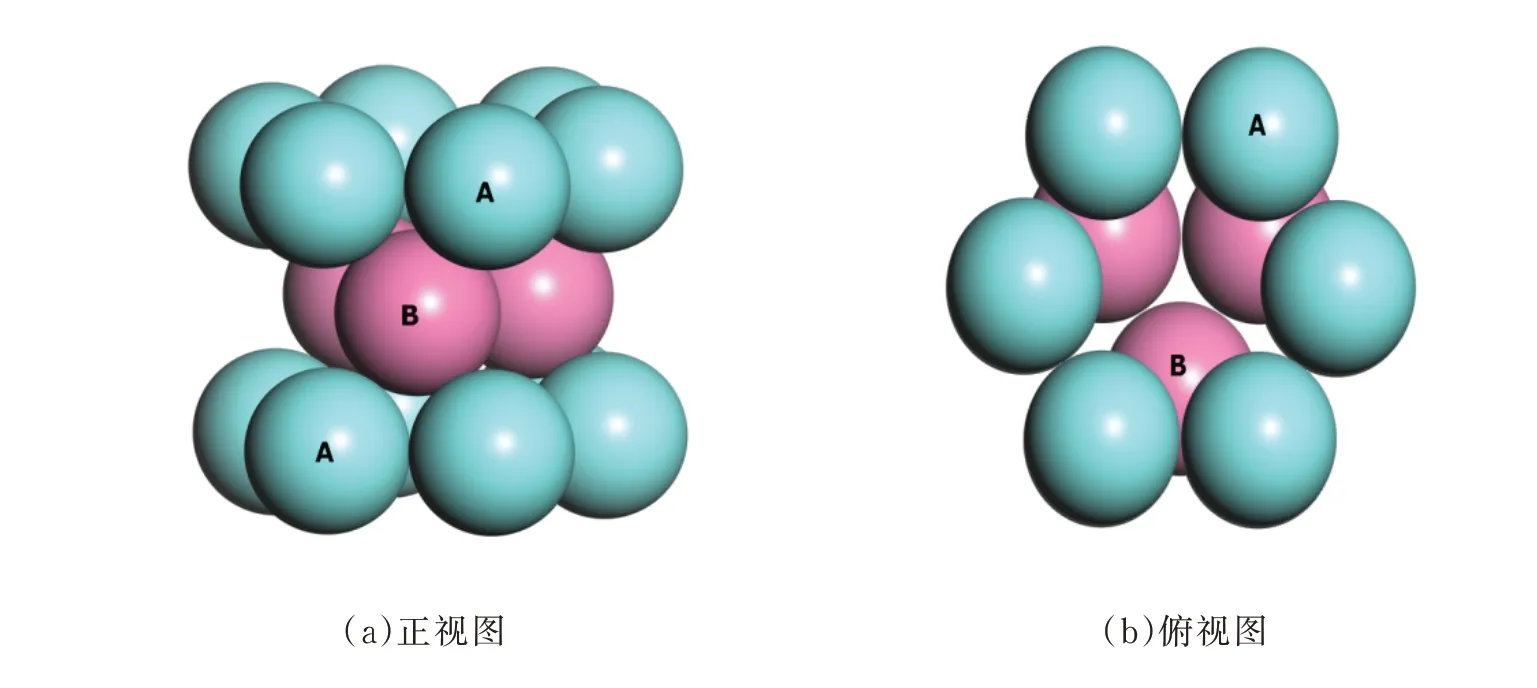
图1 钆原子HCP 模型Fig.1 HCP model of gadolinium
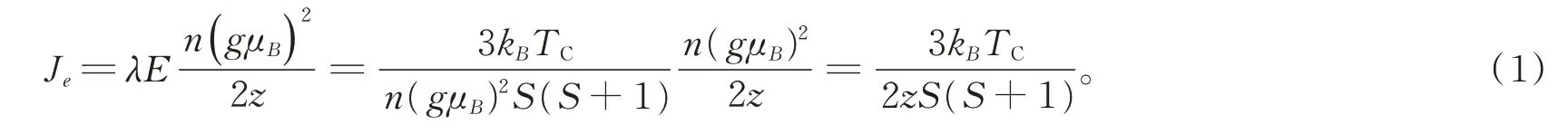
在HMC 算法中,蒙特卡罗时间τ是虚构的时间,而哈密顿量中的磁性系统自由能F[M]/(kBT)有多个波峰和波谷。磁性系统的自由能需要克服众多能量势垒从而达到亚稳态或者稳态。磁晶各项异性能加限制势能可表示为
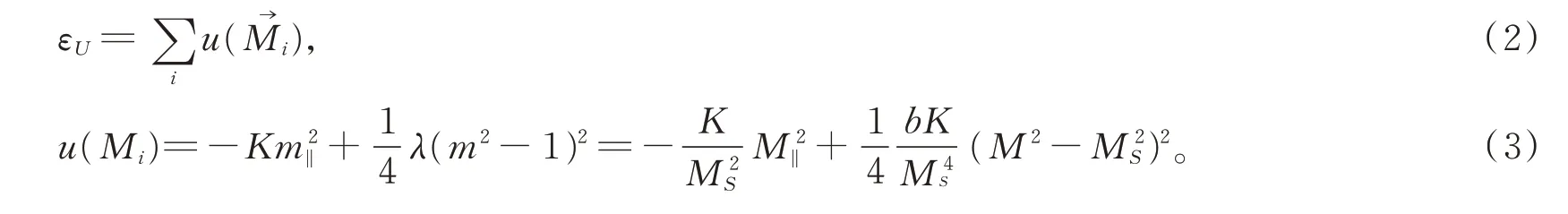
其中:m=为拉格朗日项,这一项将能量束缚在M=MS(T)附近涨落;M4是朗道二级相变中的双势阱。参数λ=bK,其中b是无量纲常数,当λ→∞时,可回到传统微磁学中磁矩归一化情形。
2 模拟结果
Gd 在室温下是顺磁性的,课题组利用上述原子尺度蒙特卡罗微磁学方法,编制程序模拟计算得到了Gd 的饱和磁化强度,用以研究饱和磁化强度随外场和温度的变化关系。其中Gd 晶体的HMC 哈密顿量包含两项[11],原子自旋共轭动量的动能项和原子自旋的标度自由能项。
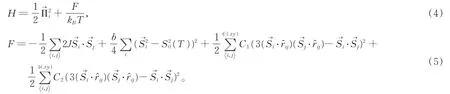

在确保系统保持铁磁相的前提下,为了在约束势中固定输入各向同性交换常数J和S0(T),不同温度情况下的模拟计算MS(T)/MS(0)值及误差大小见表1,并与文献[1]中的实验值进行比较,如图2 所示。由表1 和图2 可知,模拟值与实验值基本吻合,随温度的变化趋势也相同,Gd 单晶的饱和磁化强度随着温度增加而减小。
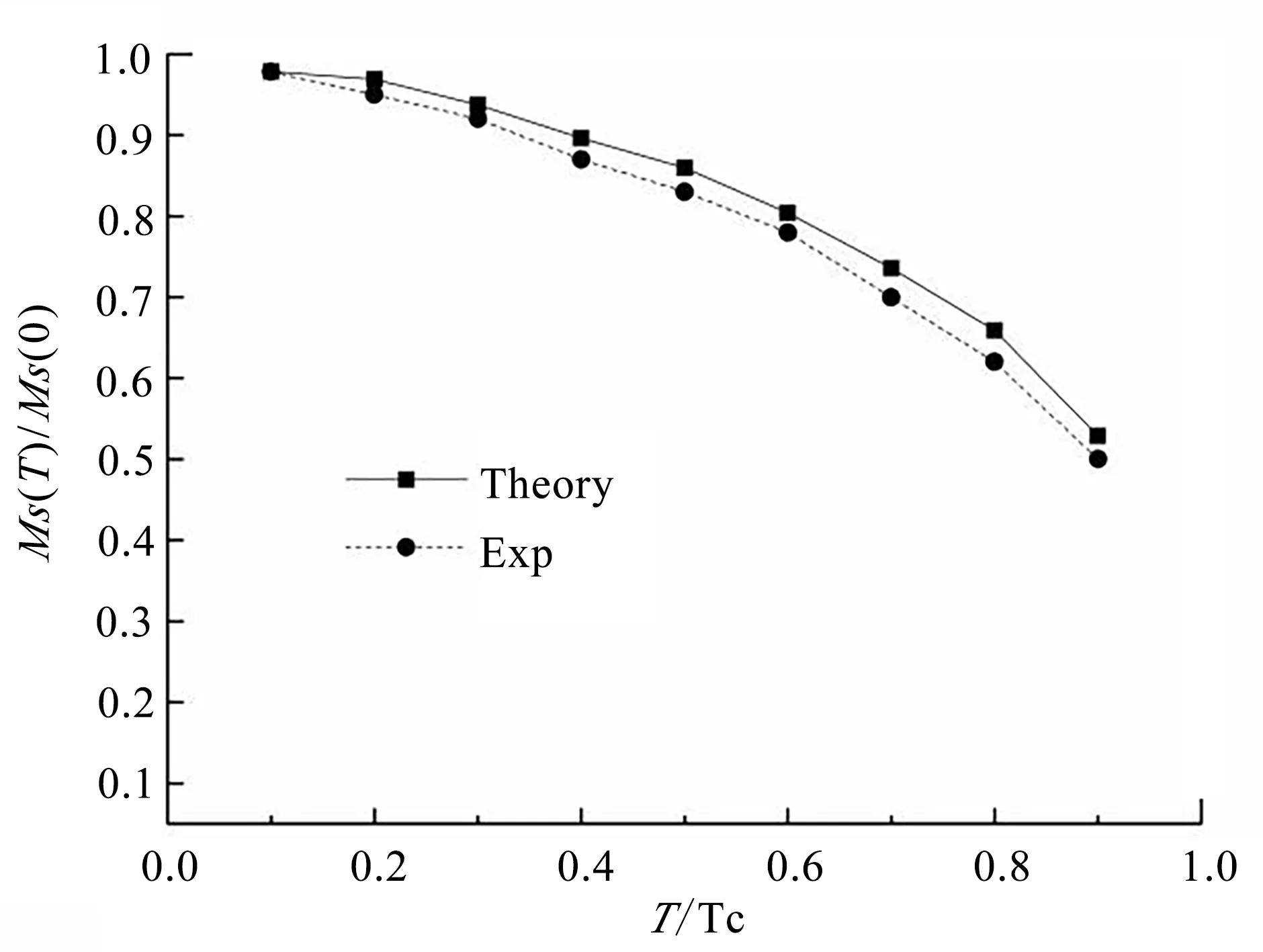
图2 MS(T)/MS(0)随温度的变化规律Fig.2 Variation of MS(T)/MS(0)with temperature
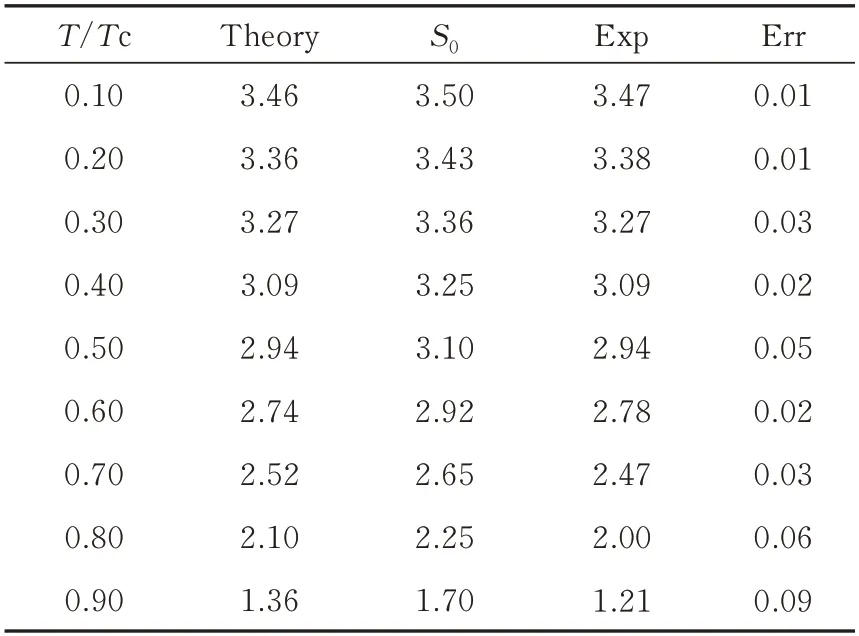
表1 不同相关温度比值下的理论值与实验值以及误差大小Tab.1 Theoretical and experimental values and error size under different relative temperature ratios
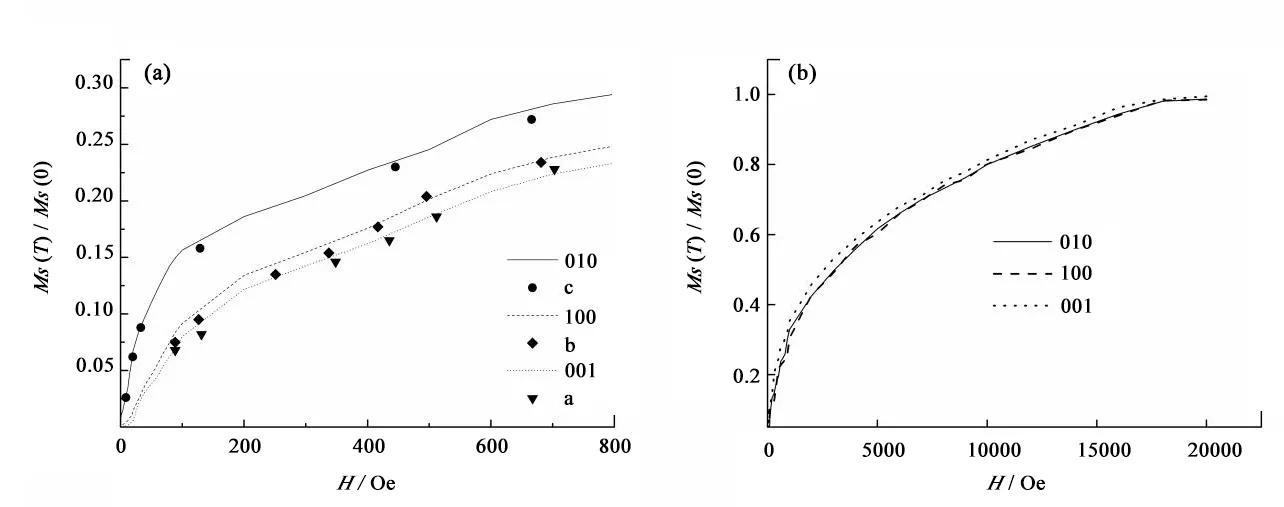
图3 MS(T)/MS(0)随着外场(H)变化规律Fig.3 The variation of MS(T)/MS(0)with external field
3 结论
本文使用原子尺度的有效自旋哈密顿量,以及混合蒙特卡罗方法得到Gd 单晶的磁化曲线,通过调节不同参数,找到接受度范围在0.7~0.9 的结果,并分别对主要参数astar,Mwarm,Nstep,dt进行调试,找到与理论相近的实验参数。通过得到磁化曲线,可以清楚地知道饱和磁化强度随着外场和温度的明显变化,这为以后对类似钆的铁磁性物质和其它顺磁等磁性物质的研究奠定了一定的理论基础。