基于粗糙集-G1法组合赋权的变压器健康状态评估

袁婉玲，崔子轩，禹洪波，邹晓松，熊炜，袁旭峰

(贵州大学电气工程学院，贵阳市 550025)

0 引 言

变压器的健康状态对电力系统的可靠运行来说至关重要。构建一套变压器可靠性状态评估管理体系，能够准确评估变压器的健康状态，合理规划维修策略[1]。

近年来，国内外对变压器状态评估有以下3种主流方法：

1)第1类以企业标准状态评价导则[2]为基础展开，此类方法简单易懂，但是权重确定和状态评估方法刻板，权重等级少，评价工作量大。

2)第2类是以大数据技术为基础，基于智能算法的状态评估方法，如神经网络[3]、故障树法[4]、灰色关联度法[5]等，这类方法在面对小样本数据时有一定的局限性，且受数据是否真实完整的影响极大，不擅于挖掘潜在联系。

3)第3类针对变压器是一个典型的灰色系统，目前普遍采用模糊集[6]、证据理论[7]等处理不确定性、不完整性的方法进行状态评估。然而，此类方法难免依赖一些不易获得的如模糊隶属函数以及统计概率分布的数据信息或者先验知识。

针对以上方法的不足之处，本文构建一个较为完善的变压器健康状态指标体系。采用客观修正主观方法结合粗糙集和G1法对各状态量赋权，解决权重分配不合理的问题，根据变压器健康指数模型确定其状态等级。最后用7台变压器实例验证本文所构建指标体系、权重确定方法及健康指数模型的合理可靠性。

1 变压器健康状态指标体系

反映变压器健康状态的信息类型复杂繁多，在构造变压器健康状态指标体系时，要综合各项指标的实际情况以及对变压器整体状态的影响选取恰当的状态量来描述变压器健康状态。

参照《中国南方电网电力设备预防性试验规程》中变压器相关试验的规定，遵循完善性、科学性、可执行性和递进性的原则，本文构建的变压器健康状态指标体系由6个部分组成，如图1所示。

图1 变压器健康状态指标体系Fig.1 Transformer health status index system

经研究发现变压器电气试验项目可以反映变压器是否存在导通故障或绝缘缺陷。变压器套管是箱外的关键绝缘设备，冷却系统可以消散变压器油的热量。一旦其中一个附件出现问题，变压器同样不能独善其身。因此在文献[8]的基础上加上包含绕组直流电阻相间最大变化率、吸收比和极化指数、绕组介电损耗、铁芯接地电流、绕组泄漏电流变化率及局部放电7个电气指标，并选取调压开关加上套管及冷却系统作为附件指标。

2 变压器健康指数模型

变压器健康指数模型的构建以变压器的基本信息为根本，以试验数据为支持，计算出变压器在目前和未来一段时间内的健康状况[9]。健康指数H通常限定在0～10，变压器的健康状态越好其值越低，如表1所示。

表1 健康指数状态等级Table 1 Health index status level

通过分析和处理变压器运行参数、状态信息，外部环境因素以及各试验数据，本文将变压器健康指数H分为以下6个部分。

2.1 老化健康指数H1

绝缘的老化是导致电力变压器老化的主要原因。文献[10]参照英国EA电力公司设备老化经验公式，根据负荷率与环境等级对老化常数B制定修正系数，得到如下老化健康指数：

H1=H0×e(B·fL·fE·ΔT)

(1)

式中：fL为负荷率修正系数；fE为环境修正系数[10]；H0=0.5为变压器初始健康指数；ΔT为变压器运行年限。

2.2 油色谱健康指数H2a

油色谱健康指数H2a主要反映变压器内部运行状态，H2a根据油色谱试验中气体H2、CH4、C2H4、C2H6、C2H2的含量等级V[8,10]及其权重ω组合得到。各气体权重的确定参照第3节。最后，根据每种气体的得分S之和，得到油色谱健康指数。

Si=Viωi

(2)

H2a=SH2+SCH4+SC2H6+SC2H4+SC2H2

(3)

式中：Si、Vi、ωi分别为气体i的得分、等级和权重。

2.3 油质健康指数H2b

油质健康指数H2b[8,10]主要反映绝缘油的品质。H2b的计算根据油质试验中击穿电压、酸值、微水的含量和相应权重得到。

与H2a的计算过程相同，得到H2b的计算公式如下：

H2b=Sm+Sa+Sb

(4)

式中：Sm、Sa、Sb分别为击穿电压、酸值、微水的得分。

2.4 糠醛健康指数H2c

糠醛健康指数由文献[8]中的论述可推导出：

H2c=2.33×(FFA)0.68

(5)

式中：FFA为绝缘油中的糠醛值。

2.5 电气健康指数H2d

文献[8]中构造的健康指数H1、H2a、H2b、H2c，能反映变压器绝缘材料的老化、劣化过程[11]。

根据本文提出的电气指标构造的电气健康指数H2d能反映变压器绝缘油受潮以及过热、放电、受潮等故障类型，能发现各种绕组接触、电流回路是否短路、铁芯多点接地等问题[12]。如果没有在故障发展的初期及时发现并检修，会导致后期变压器发生故障，引起不必要的亏损。

利用粗糙集计算时必须把数据划分成离散型，根据行业标准以及实际故障经验并参照文献[13]，本文将电气指标划分成6个等级，如表2所示。同样，得到H2d的计算公式如下：

表2 电气指标等级划分Table 2 Classification of electrical indicators

H2d=S1+S2+S3+S4+S5+S6+S7

(6)

式中：S1～S7依次为电气试验部分7项目指标的得分。

2.6 附件健康指数HF

将套管、调压开关以及冷却系统3个附件都单独作为一个附属设备进行评估。同时要分析附件健康状况与变压器健康状况之间的关系来修正变压器的评估结果。

借鉴老化经验公式，结合3个附件相应修正系数，得到套管、调压开关、冷却系统的健康指数分别为：

HG=F1×F2×H0×eB·fE·ΔT

(7)

HT=F3×H0×eB·fE·F4·ΔT

(8)

HL=F5×F6×H0×eB·fE·ΔT

(9)

式中：F1、F2分别为套管介损修正系数和电容量修正系数；F3、F4分别为调压开关可靠性系数和操作系数[8]；F5、F6分别为冷却系统电机运行修正系数和渗漏油修正系数。各项系数的制定如表3—5所示。套管、调压开关、冷却系统的权重分别为ω1、ω2、ω3。可得附件综合健康指数为：

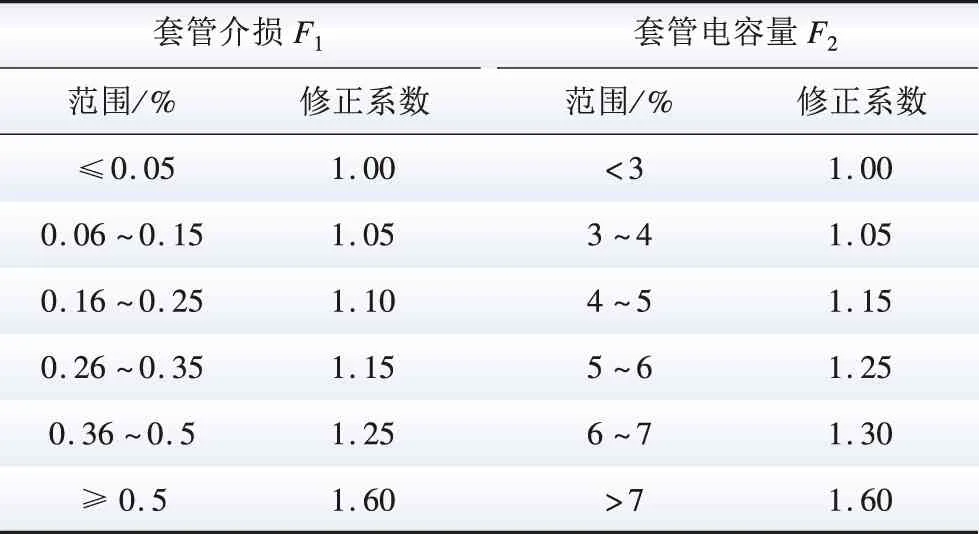
表3 套管修正系数Table 3 Casing correction factor

HF=ω1HG×ω2HT×ω3HL

(10)

表4 冷却系统电机运行修正系数Table 4 Operation correction coefficient of cooling system motor

表5 冷却系统渗漏油修正系数Table 5 Correction coefficient of oil leakage in cooling system

2.7 综合健康指数HC

计算完上述各健康指数之后，通过分析各部分因素对变压器整体健康状况的作用和影响，根据表6所示H1、H2a、H2b、H2c、H2d之间可能存在的逻辑关系确定变压器综合健康指数HC和综合修正系数fcom。

表6 fcom和HC的确定Table 6 Determination of fcom and HC

分析HC与HF的比值关系，根据百分比区间查表获得附件修正系数fFC[8]。得到最终健康指数计算公式如下：

H=max(HC，HF)×fFC

(11)

3 指标权重的确定方法

指标权重的确定反映了变压器各个状态量在评估和决策过程中所起的作用[14]。科学合理分配指标权重是准确评估变压器健康状态的关键。

3.1 RS法计算客观权重

由于每个属性对整体的贡献程度是不一样的，粗糙集赋权法依赖于各属性的实际试验数据，根据属性在变压器上的属性重要度得到指标权重，权重值会随着数值的变化而变化，因此用于反映指标的客观信息。该算法首先删除一个属性，然后考虑在没有该属性的情况下分类将如何变化。若删除某一属性之后分类明显不同，则该属性的重要性较高；否则，该属性的重要性较低[15]。根据粗糙集计算各属性权重可有效降低传统计算的主观因素，提高指标体系的可靠性。

由于指标体系中基本信息和糠醛试验部分的健康指数计算公式中不需要权重的参与，因此根据粗糙集的理论知识，变压器其余部分指标客观权重的确定步骤如下(以油色谱试验指标权重的确定为例)。

1)状态等级划分：变压器油色谱健康状态对应整体决策系统S=(U,A,V,f)，其中论域U={u1,u2,…,ui},i=1,2,…,s为研究对象的非空有限集合，s为变压器状态评价样本数。条件属性C={a1,a2,…,a5}对应5个油色谱健康指标。决策属性D={d}为变压器状态评价等级，本文将健康状态分为6个等级，设V={1,2,3,4,5,6}中各元素为健康、亚健康、注意、异常、严重、超出老化范围6个状态，且C∩D=∅。

2)条件属性与决策属性的匹配：在样本数据s中，每个样本数据的各条件属性(状态量ai)都对应唯一的状态等级，且有决策属性等级(变压器整体状态等级)与条件属性集匹配。具体由每个样本油色谱指标的试验数据对照第2节中的等级划分表可得到指标等级，等级0、2、4、6、8、10分别对应条件属性的状态等级1、2、3、4、5、6。决策属性等级同理可得。

3)计算各状态量的权重[16]：将论域U用粗糙集划分成不同的等价类别，根据公式(13)和(14)求得状态量ai的下近似和正域：

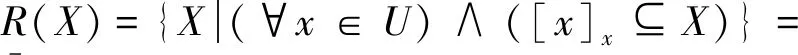
(12)

(13)

根据正域求得决策属性D对条件属性C的依赖度γC(D)和剔除某一属性Ci后，决策属性D对条件属性C-Ci的依赖度γC-ai(D)。

(14)

式中:|U|为论域U的基数。

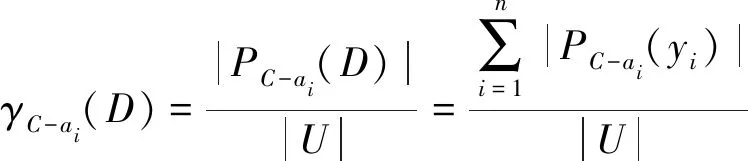
(15)

再根据依赖度求得第i个属性ai对决策属性D的重要度σCD(ai)：

σCD(ai)=γC-ai(D)-γC(D)，i=1,2,…,n

(16)

通过归一化运算得到第i个条件属性ai的客观权重ωai为：

(17)

3.2 G1法计算主观权重

G1法是对层次分析法的改进，能灵活反映各项指标的权重，计算过程清晰简便[17]。采用G1法得到变压器指标主观权重的步骤为：

1)建立序关系：专家根据准则规定及工作经验对n个状态指标的相对重要程度排序，得到a1>a2>…>an-1>an的序关系。

2)Rk为相邻指标的相对重要程度之比，专家根据经验及标准[18]对Rk赋值。

(18)

3)指标ai的主观权重为：

(19)

4)根据ωσi推出其他指标的主观权重

ωσ(i-1)=ωσiRk

(20)

3.3 客观修正主观的权重优化组合

粗糙集对于问题的描述较为单调。而G1法较依赖专家的经验，主观因素较大。为了使权重的分配愈加合理化，尽可能减小评估系统在变压器健康状态决策过程中的误差[19]。用客观修正主观方法结合RS和G1的组合赋权步骤如下：

1)专家根据各个指标的重要性建立序关系，以反映G1法在属性排序上的优势。

2)根据式(17)粗糙集客观赋权的属性重要度确定主观赋权所需要的相邻指标重要性之比Rk，如式(22)所示，体现了客观赋权法在反映指标数据信息上的优势。

(21)

3)最后，采用G1主观赋权法计算各指标的优化组合权重ωi。

(23)

ωi-1=ωiRk

(24)

综上可以看出，本文权重组合方法中客观赋权和主观赋权相互嵌套，采用客观赋权的属性重要度确定主观赋权中相邻指标重要性之比，利用数据信息对专家意愿进行修正，改变了传统的权重相加相乘组合方式，可解释性强。主观权重能反映指标自身的重要性，客观权重能反映数据的信息，组合优化权重能有效结合上述主客观权重的优点，在优化过程中，能充分体现客观权重在区分度上的优势，合理反映指标的重要性[20-21]。

4 实例分析

本文选取了7台电压等级、运行年限均不同的变压器作为实例分析对象，为验证本文所提变压器健康状态评估方法的准确可靠性，制定如表7所示的6种方案。根据第3节计算出分别采用AHP、文献[20]中RS+AHP、本文RS+G1权重确定方法的各指标权重如表8所示。

表7 制定对比方案Table 7 Comparison plan

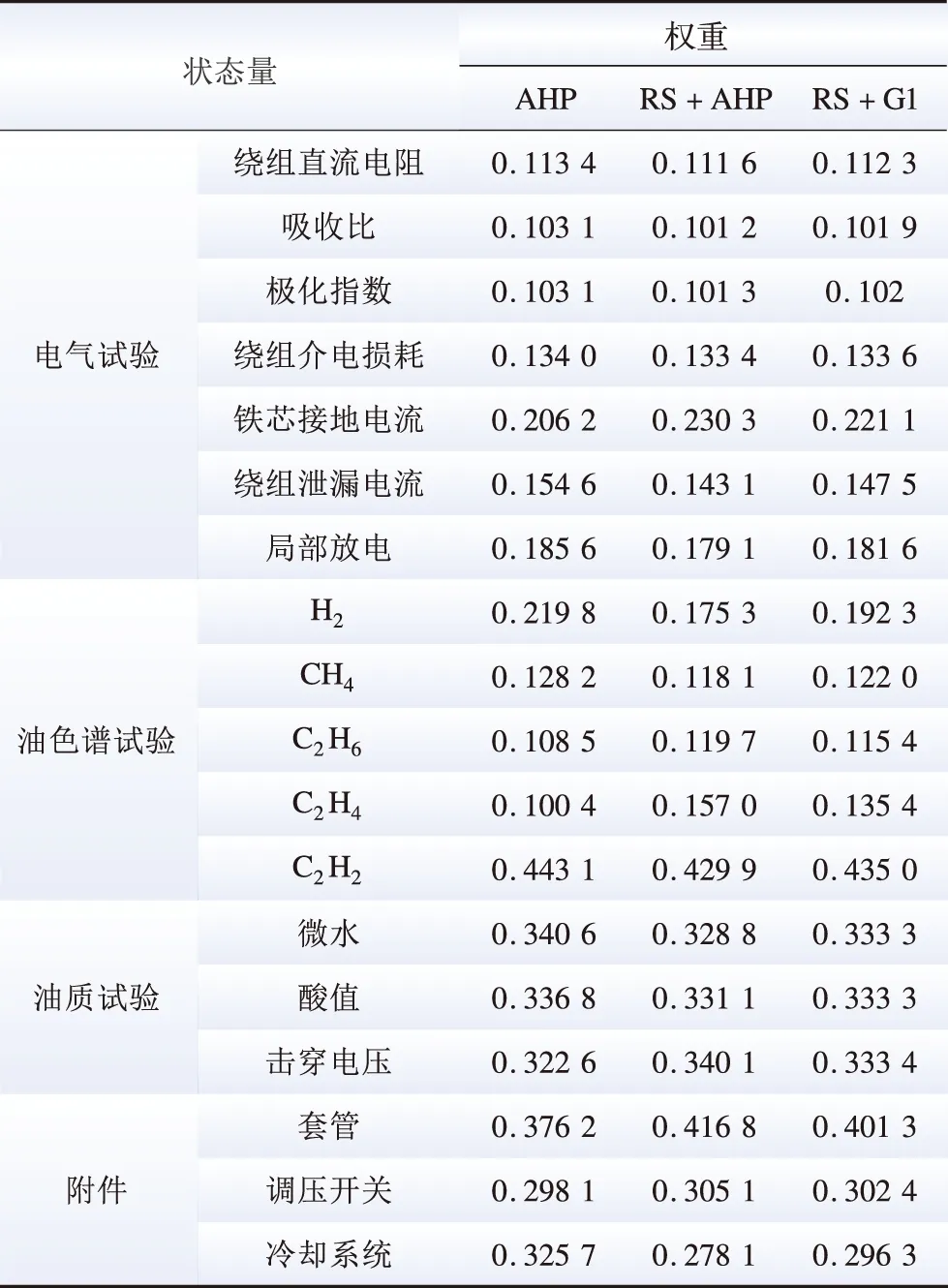
表8 状态量权重Table 8 State weight

根据第2节的计算流程及公式，将不同方法所得权重代入健康指数模型中，得到7台变压器在6个方案下的健康指数及健康状态等级，结合变压器实际状态参照表1的描述及等级得到表9所示结果和表10所示总体判断情况。

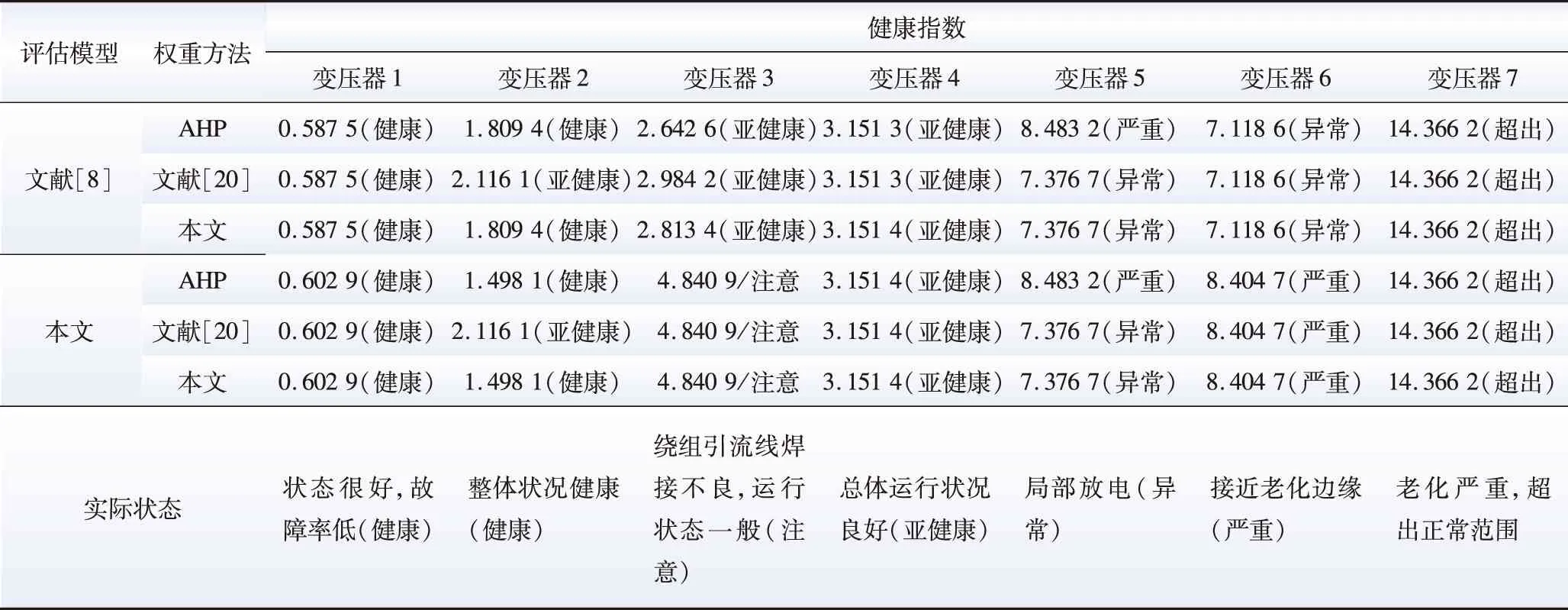
表9 健康指数计算结果Table 9 Calculation results of health index

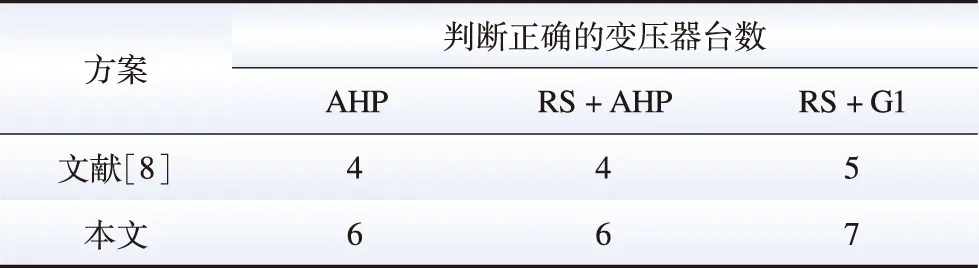
表10 6种方案下判断正确的变压器台数Table 10 Correct number of transformers judged under six schemes

1)分析表9计算结果可以看出，3、6号变压器在文献[8]模型下的健康评价状态不符合实际，而通过本文模型计算出的健康状态同实际情况一致。

2)2号变压器在使用文献[20]中RS+AHP法确定的权重时，其健康状态不符合实际情况，当使用本文所提RS+G1优化组合所赋权重时，状态为健康与实际相符。5号变压器在只通过AHP法确定的权重进行计算时，其健康状态为严重与实际状态不符，用本文组合权重时为异常，判断正确。

3)由表10可看出，文献[8]模型和本文构建指标模型分别搭配3种不同权重时，使用本文RS+G1权重组合优化方式判断正确的变压器台数多；当权重方法相同，指标模型不同时，本文模型相对于文献[8]模型判断正确的变压器台数多。

综上所述，分析1)、3)表明了本文指标体系的合理性及正确性。分析2)、3)说明单一的权重方法或权重组合方式不合理会导致权重分配不能真实反映指标对变压器健康状态的实际影响。当综合考虑两种因素且采用本文所提优化组合时，能有效、科学地计算指标权重，评估准确率高。分析3)可表明变压器健康状态指标体系越全面、权重确定方法越合理，判断变压器健康状态的正确率也会随之增加。

首先，本文所构建的变压器健康状态指标体系更加完整，能反映出传统指标模型不能体现的变压器缺陷。其次，本文使用粗糙集来确定指标客观权重，不需要其他先验信息，依赖于属性试验数据且不要求样本数量，降低了赋权工作的复杂性，客观地对不确定性决策系统进行描述和处理。最后，采用客观修正主观的方式得到组合优化权重，计算过程相互融合，兼顾了主客观权重方法的优势，相比文献[20]中RS+AHP的优化模型结合方式更加合理。

上述分析验证了本文所构建的变压器健康指数评估指标体系以及粗糙集-G1客观修正主观优化组合赋权方案得到的评估结果是符合变压器实际情况的，提高了变压器健康状态评估的可靠性和准确率。

5 结 论

本文构建了较为完善的变压器健康状态指标体系，将指标体系的各个部分对应量化为6个健康指数构建健康指数模型。采用G1法和粗糙集分别确定指标主客观权重，用客观修正主观的组合方法对指标合理赋权，最后以7台不同运行年限、不同等级的变压器为例计算健康指数并得到状态等级，通过分析结果得到如下结论：

1)本文变压器健康状态指标体系能正确反映变压器的缺陷又不复杂。在同一种权重方法下本文变压器指标体系对应的状态评估正确率高。

2)粗糙集基于实际数据进行计算，能更客观地表示指标的重要程度。G1法在AHP基础上更加清晰简便。

3)在同一评价模型下，本文客观修正主观的权重组合方法新颖且可解释性强，比单一赋权法或其他组合方式的优化权重评价准确率更高，避免了分配权重的主观依赖性和片面性问题。

以上结论表明本文的变压器健康状态指标体系以及粗糙集+G1优化组合的赋权方法能准确可靠地判断变压器健康状态，提高电网运行可靠性，为以后电力变压器的健康状态评估提供了参考。